RADIO-AIDE

3e COPIL - WP3

Alain TROUVÉ & Anton FRANÇOIS

ENS Paris Saclay - Centre Borelli

Objectifs Initiaux

Retrouver l'historique des pixels dans le temps.
Analyser les composantes géométriques longitudinales. (compression, dilatation, ré-allocation)

Metamorphoses

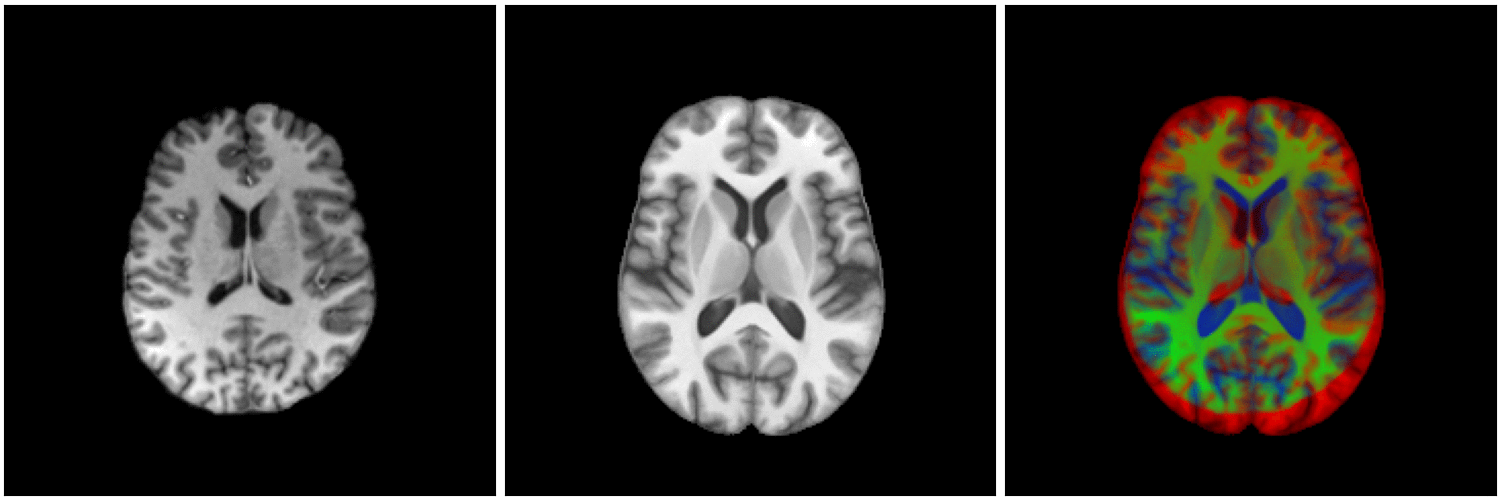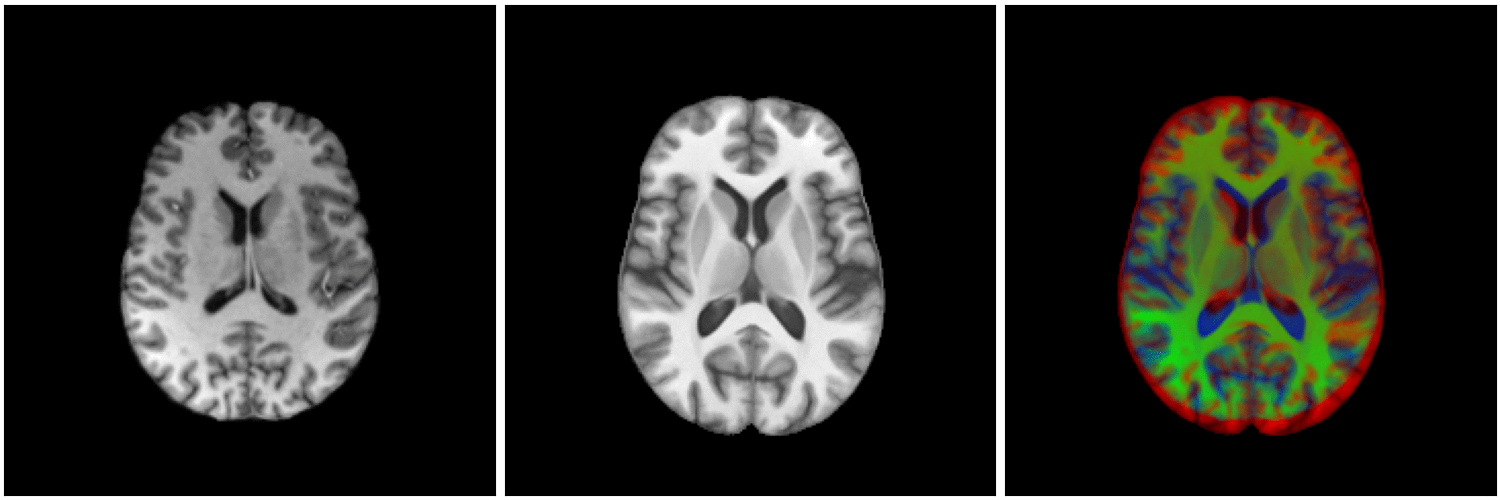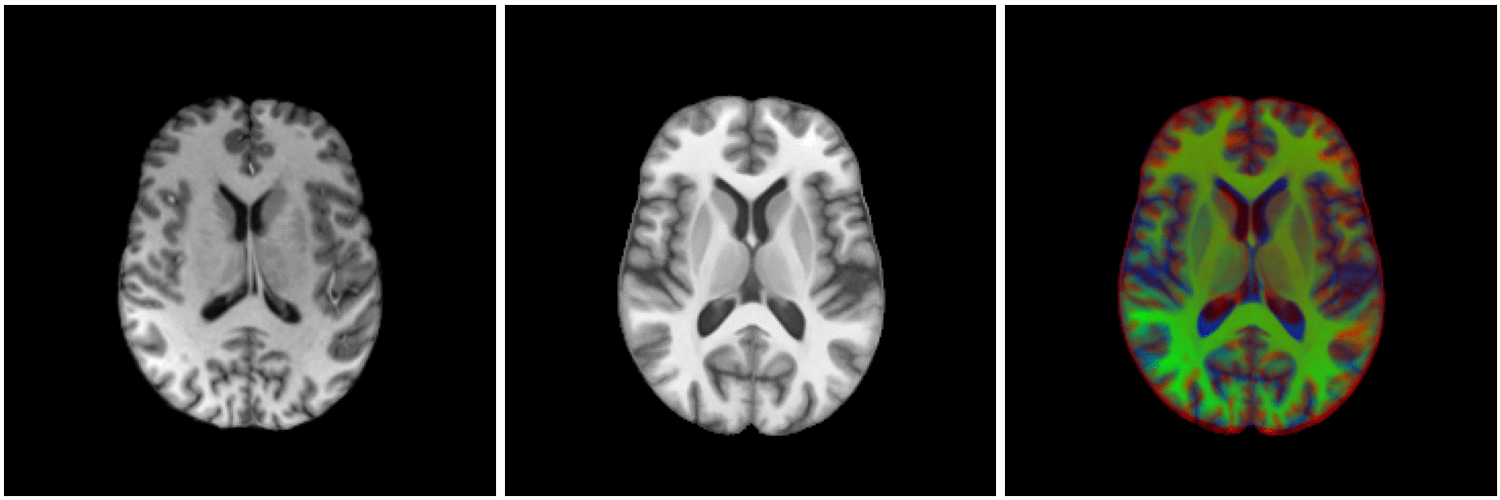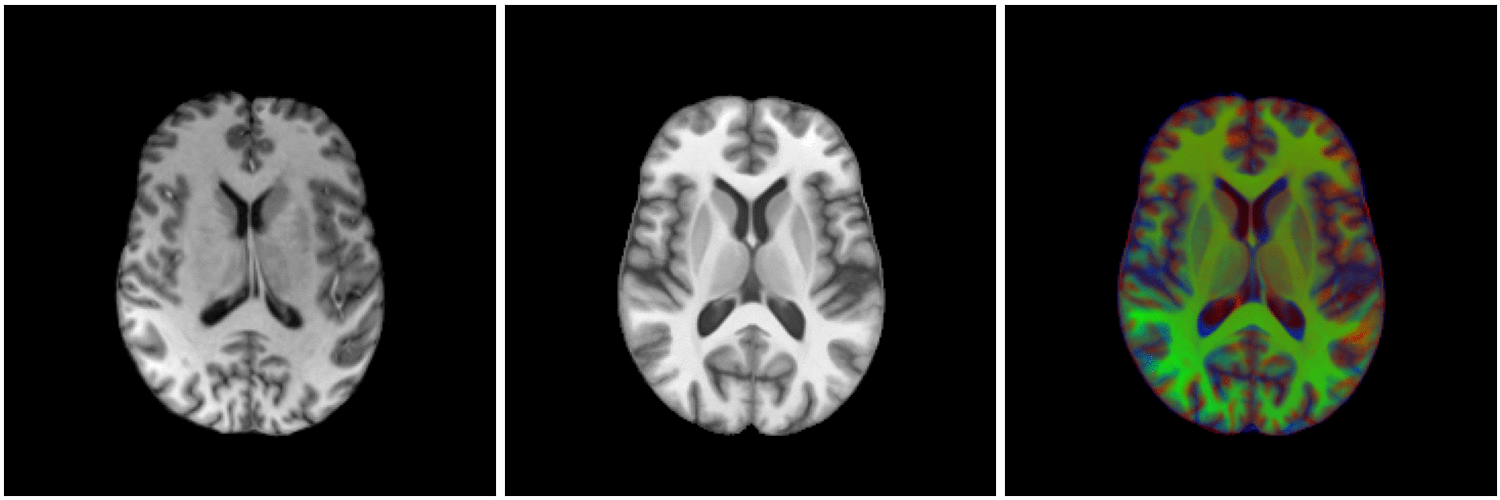
non-linear image registration:

Image registration

temporal

Anton François - 12/02/2025

Metamorphoses : En Bref

LDDMM can reach only images with same topology

Ajoute des intensité ou ré-alloue des classes. Permettant des changements de topologies.

\[\partial_t I_t = \sqrt{\rho}v_t \cdot \nabla I_t\]

\[+ \sqrt{1 - \rho} z_t\]

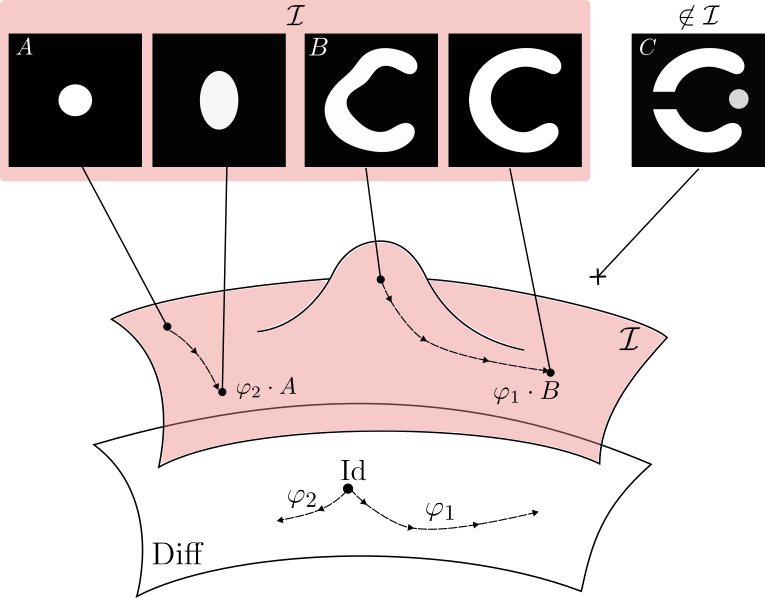
Topology and appearances variations

Anton François - 12/02/2025

Metamorphoses : En Bref

Metamorphoses

Deforme à l'aide d'un flot de champs de vecteurs

Metamorphosis

Source

Target

LDDMM

Anton François - 12/02/2025

Metamorphoses : En Bref

Découpage du Projet:

Fournir un package stable et documenté.
Théoriser & Implementer les Métamorphoses sur le simplex.
Contrôle de la balance déplacement vs Réallocation
Pré-processing recalage rigide.
Couplage recalage Métamorphoses + Rigide
Analyse longitudinale

Découpage du Projet:

Fournir un package stable et documenté.

Découpage du Projet:

2. Théoriser & Implementer les Métamorphoses sur le simplex.

The standard $n$-Simplex is the subset of $\mathbb R^{n+1}$ given by

$$\Delta^n = \left\{p \in \mathbb R^{n+1} : \forall i \in \{1,\cdots,n+1\}, p_i > 0; \sum_{i=1}^{n+1} p_i = 1\right\}.$$

A path on the 2-Simplex

fig from [Jasminder, 2020]

Why the simplex rather than images:

pixel colour does have a "meaning"
Does not change depending on the preprocessing => Data confidence increased
notion of uncertainty

Data from :

Let $q$ be the "simplex image", ($q(x) \in \Delta^n$) and $\tilde q : \Delta^n \mapsto S^n = \sqrt q$ the isometry from the simple on the sphere. We set its evolution such that:

\[\partial_t\tilde q = -\sqrt{\rho} \nabla \tilde q \cdot v + \sqrt{1 - \rho} z; \qquad\rho \in \mathbb R\]

Let $H$ be the Hamiltonian defined such that,

\[H(\tilde q,p,v,z) = (p|\partial_t \tilde q) - \frac 12\|v\|_V^2 -\frac 12\|z\|_2^2\]

By computing the variations of H with respect to $\tilde q,p,v,z$ we retrieve the geodesic equations

$$\left\{\begin{array}{rl} \dot {\tilde q_t} &= - \sqrt{\rho} \nabla \tilde q_t \cdot v_t + \sqrt{1 -\rho} z_t\\ \dot p_t &= - \sqrt{\rho} \mathrm{div}(p_t \otimes v_t) - \sqrt{1 -\rho}<p_t, \tilde q_t>z_t\\ z_t &= \sqrt{1 - \rho} (p_t - (\sum_{i=1}^{n+1} p_{t,i} \tilde q_{t,i})\tilde q_t)\\ v_t &= - \sqrt{\rho} K_V\left(\sum_{i=1}^{n+1} p_{t,i}\nabla \tilde q_{t,i} \right)\end{array}\right.$$

Metamorphosis on the Probability simplex

$\rho = 1$ Pure Déformation

$\rho = 0$ Ré-allocation

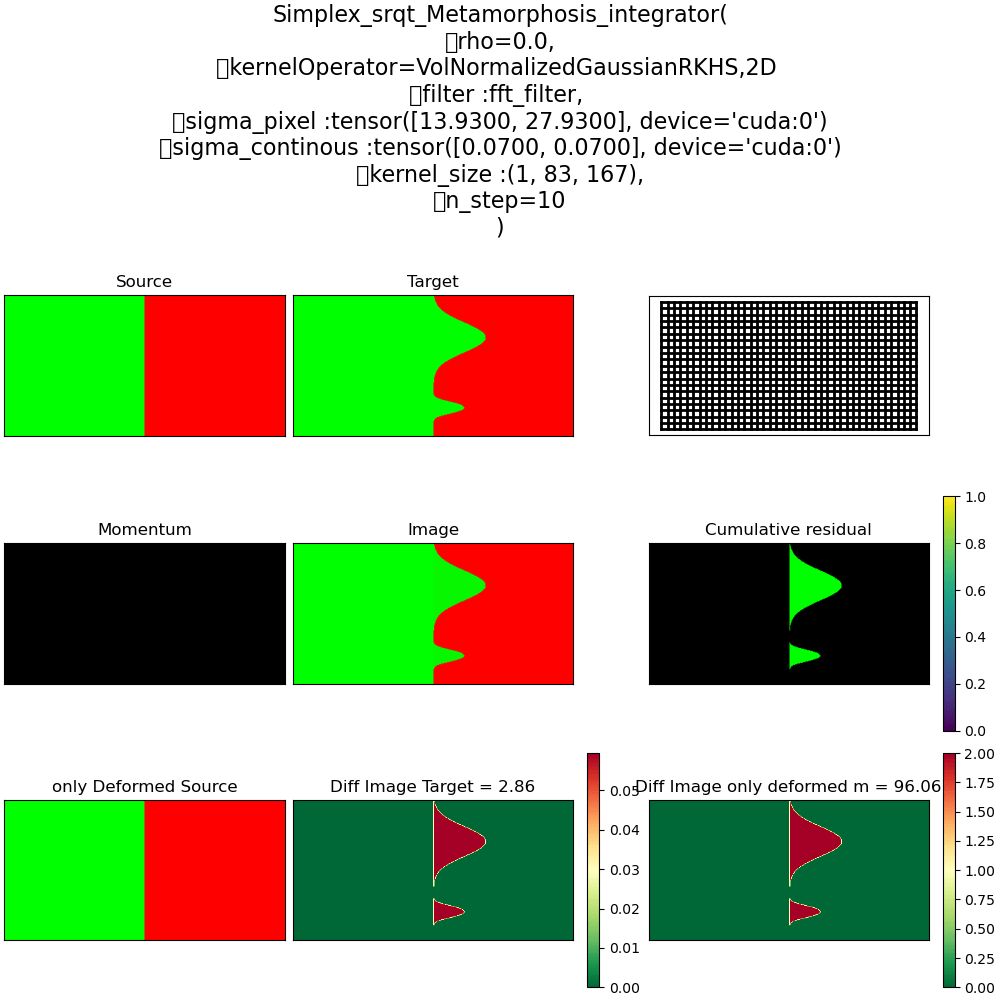
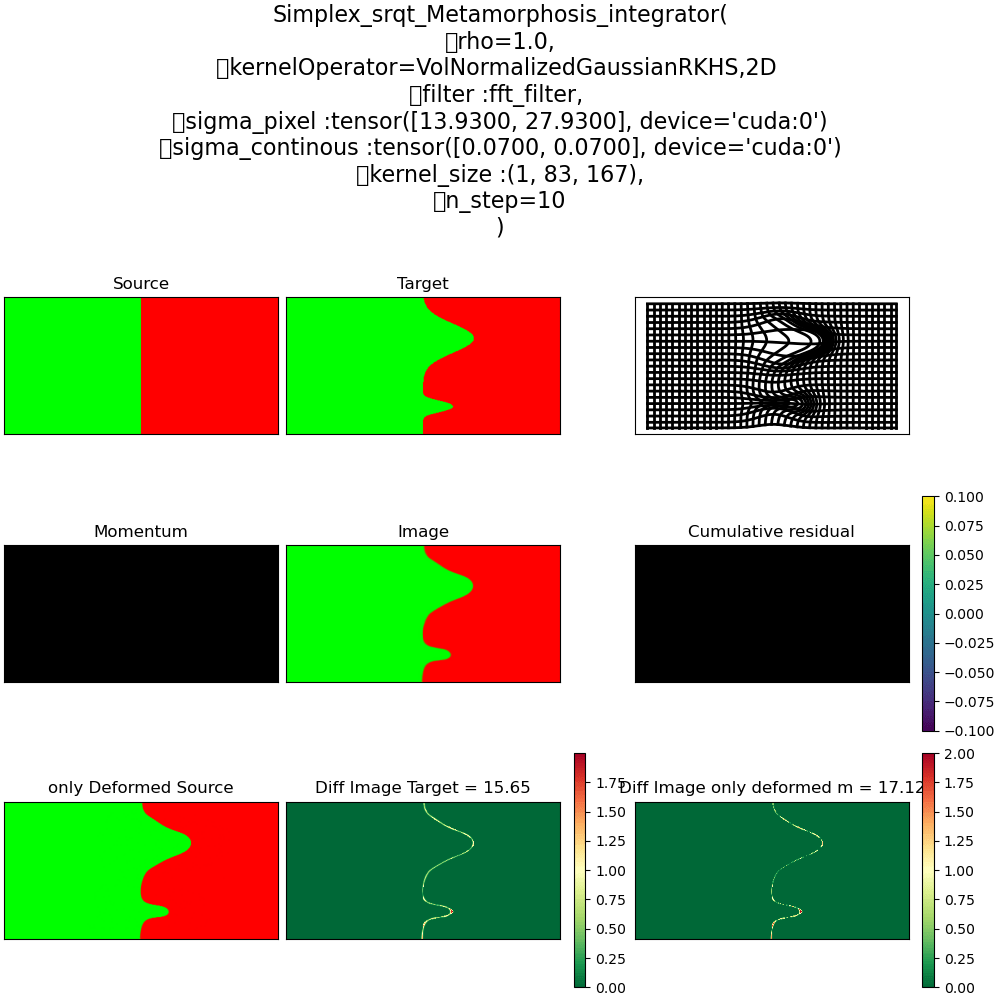
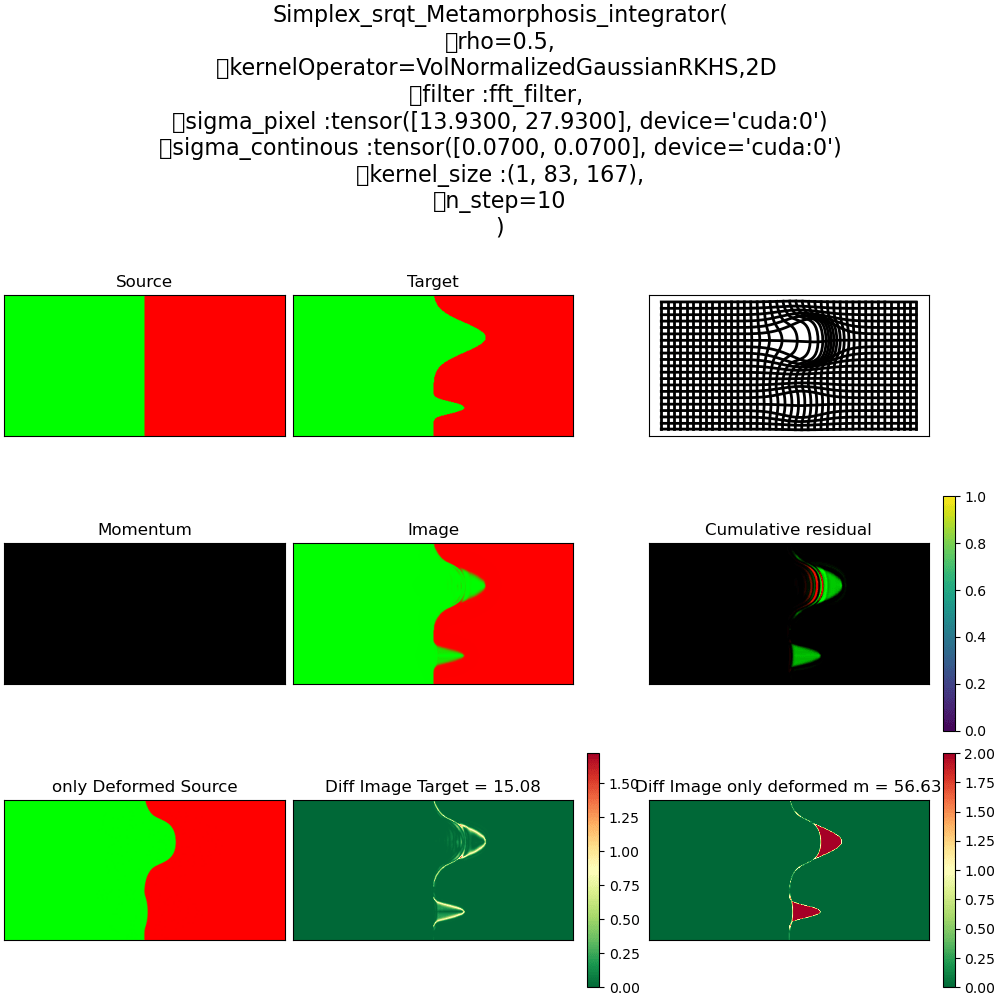
$\rho = 0.5$ Pure Déformation

Nous avons besoin de vous !:

Pour choisir des paramètres qui ont du sens par rapport aux Glioblastomes.

3. Contrôle de la balance déplacement vs Réallocation

Isométrie par rapport à la taille de l'image
Meilleur contrôle des paramètres. $(\sigma, \rho)$

Découpage du Projet:

Nouveaux Noyaux

Anisotropric volume normalized Gaussian kernel
Let $\sigma=(\sigma_h)_{1\leq h\leq d}$ be the standard deviation along the different coordinate in $\mathbb R^d$ and $B=B(0,1)$ the closed ball of radius 1. We denote $D=\text{diag}(\sigma_h^2)$ and we consider the kernel
$$K_{AVNG}(x,y)=\frac{1}{\mathrm{Vol}(D^{1/2} B)}\exp\left(-\frac{1}{2}\langle D^{-1}(x-y),(x-y)\rangle\right)D.$$
call the anisotropic volume normalized gaussian kernel (AVNG kernel).

3. Contrôle de la balance déplacement vs Réallocation

Découpage du Projet:

$$K_{AS-ANG}(x,y) = \int_{0}^{k+1} K_{{AVNG}}(x,y;2^{-u}\sigma ) du$$

All Scales - Anisotropic Normalised Gaussian Kernel

is a continuous Integration of the $K_{AVNG}$ kernel:

3. Contrôle de la balance déplacement vs Réallocation

Découpage du Projet:

Découpage du Projet:

4. Pré-processing recalage rigide.

Stage avec Clara TROMPETTE

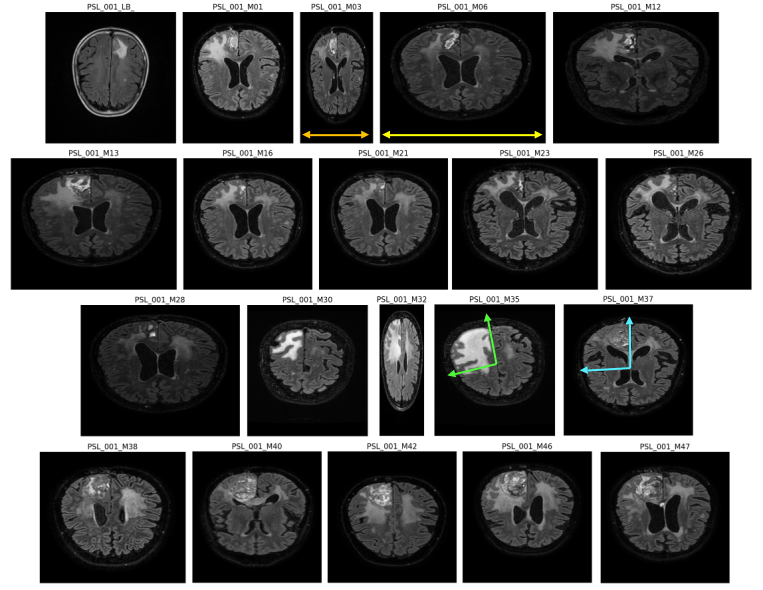
Initialement, les images ne sont:

- Pas alignés les unes aux autres.

- Pas échantionnées également

Découpage du Projet:

5. Couplage recalage Métamorphoses + Rigide

Collaboration avec Thomas PIERRON et Rayane MOUHLI

Découpage du Projet:

6. Analyse longitudinale

Metamorphose : Chemin Geodésique.

Découpage du Projet:

6. Analyse longitudinale

Metamorphose : Chemin Geodésique.

Découpage du Projet:

6. Analyse longitudinale

Metamorphose : Chemin Geodésique.

Découpage du Projet:

6. Analyse longitudinale

Metamorphose : Chemin Geodésique.

Le recalage n'est jamais exact.

Régularité des trajectoires ?

Il reste beaucoup de questions ouvertes