Topological Data Analysis
for Train-Free
Glioblastoma Segmentation in MRI


Raphaël Tinarrage and Anton François
Advantages and Potential Impact


Glioblastoma Segmentation
Problem Definition

Glioblastoma Segmentation
Locate and label brain cancers.
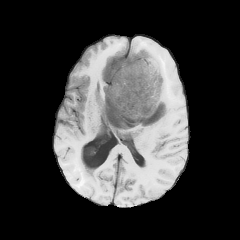
Have access to four modalities
Use the BraTS2021 data-set
Provide segmentation ground truth.
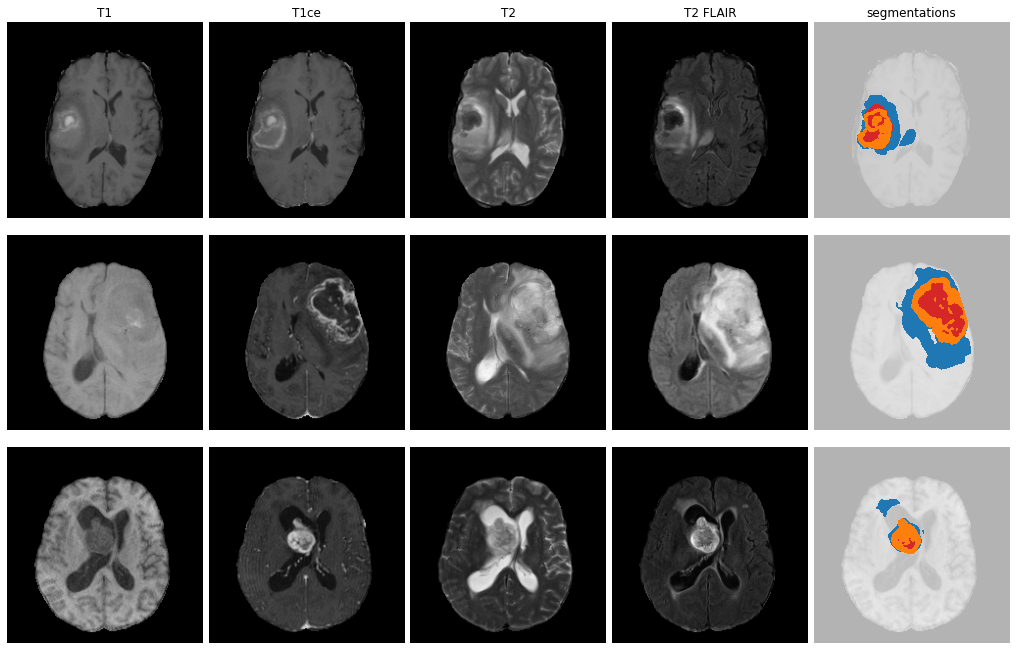
ET - GD enhancing tumour
ED - Peritumoural edematous/invaded tisue
NRC - Necrotic Tumour Core
Introducing TDA
as tools for Images
Introducing TDA
as tools for Images
- Singular Homology
- Filtrations
- Persistence diagrams
Singular Homology:
We use the singular homology in \(\mathbb{Z}/2\mathbb{Z}\).
Steelpillow CC BY-SA 4.0, via Wikimedia Commons
refers to the study of a certain set of algebraic invariants of a topological space \(X\), the so-called homology groups \(H_n(X)\).
Betti numbers \(\beta_i\): carry the topological interpretation
- \(H_0(X) = (\mathbb{Z}/2\mathbb{Z})^{\beta_0} \) where \(\beta_0\) is equal to the number of connected components
- \(H_1(X) = (\mathbb{Z}/2\mathbb{Z})^{\beta_1}\) where \(\beta_1\) is equal to the number of 'independent loops'
- \(H_2(X)= (\mathbb{Z}/2\mathbb{Z})^{\beta_2}\) where \(\beta_2\) is equal to the number of 'independant voids'.
Steelpillow CC BY-SA 4.0, via Wikimedia Commons
Betti numbers: carries the topological interpretation
- \(H_0\) is equal to the number of connected components
- \(H_1\) is equal to the number of 'independent loops'
- \(H_2\) is equal to the number of 'independant voids'.
- \(H_0 = (\mathbb{Z}/2\mathbb{Z})^1 \)
- \(H_1 = (\mathbb{Z}/2\mathbb{Z})^1 \)
- \(H_2 = (\mathbb{Z}/2\mathbb{Z})^1 \)
- \(H_0 = (\mathbb{Z}/2\mathbb{Z})^1 \)
- \(H_1 = (\mathbb{Z}/2\mathbb{Z})^2\)
- \(H_2 = (\mathbb{Z}/2\mathbb{Z})^1 \)
Singular Homology
\(H_0(X) =(\mathbb{Z}/2\mathbb{Z})^3\): Three connected components


\( H_1(X) = (\mathbb{Z}/2\mathbb{Z})^2 \): two holes

8x8 pixels image
Filtrations
Let \(I : \Omega \rightarrow [0,1]\) be a greyscale image, the super-level set filtration is the collection \(I^t, t\in [0,1]\), where \(I_t\) is the set of pixels with intensity greater or equal to \(t\).
Thus, \(I^t \subset I^s, t \geq s\).
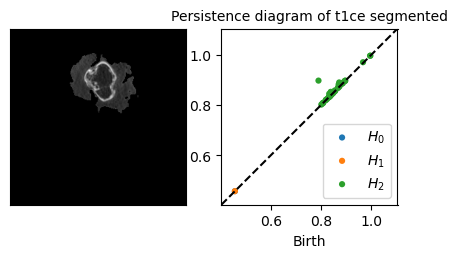
Persistence diagrams
Example:
Persitence diagram of a Brain MRI (2D)

Slice of the SRI template (left), the persistence diagram of its superlevel set filtration (right) and its most persistent \(H_0\)-cycle (middle)
Example:
Persistence diagram of a Brain MRI (2D)
Slice of the SRI template (left and middle) with the most persistent \(H_1\) -cycles, and the persistence diagram of its superlevel sets filtration.

Example:
Persistence diagram of a Brain MRI (2D)
A 3 steps method
based on
TDA and a simple model.

The



model
NRC = Necrotic Core
ET = Enhencing Tumour
ED = Edematous tissue

The



model
NRC = Necrotic Core
ET = Enhencing Tumour
ED = Edematous tissue
The



simple
model
NRC
ET
ED
The simple model



NRC
ED
ET
\(\beta_0 = 1\)
\(\beta_2 = 1\)
Pas de topologie indiquée
Step 1: Whole Tumour selection.

Step 2: ET identification
Step 3: NRC & ED identification
- Refinement -
A simple 3 steps method based on a simple model.
Step 1: Segment the whole tumour by selecting the biggest and brightest connected component.
Sum of active pixels: \(I(x) \geq t\)

Step 1: Segment the whole tumour by selecting the biggest and brightest connected component.
Step 1: Refinement. Stick to edges.

Let be \(I\) the FLAIR image, \(X\) the estimated segmentation and \(E(I)\) a Function computing edges.
edgeDice\((I,X)\) is a metric measuring the degree of edge overlap.
\( \mathrm{edgeDice}(I,X) = \mathrm{DICE} (E(I) \times E(X), E(X))\)
Step 1: Refinement. Stick to edges. + close holes.

\( \mathrm{edgeDice}(I,X) = \mathrm{DICE} (E(I) \times E(X), E(X))\)

DICE = 0.8802
Step 2: ET Identification, Find a sphere.
Step 2: ET Identification, Find a sphere.

Step 3: NCR & ED Identification, by distinguishing the outside and insides.
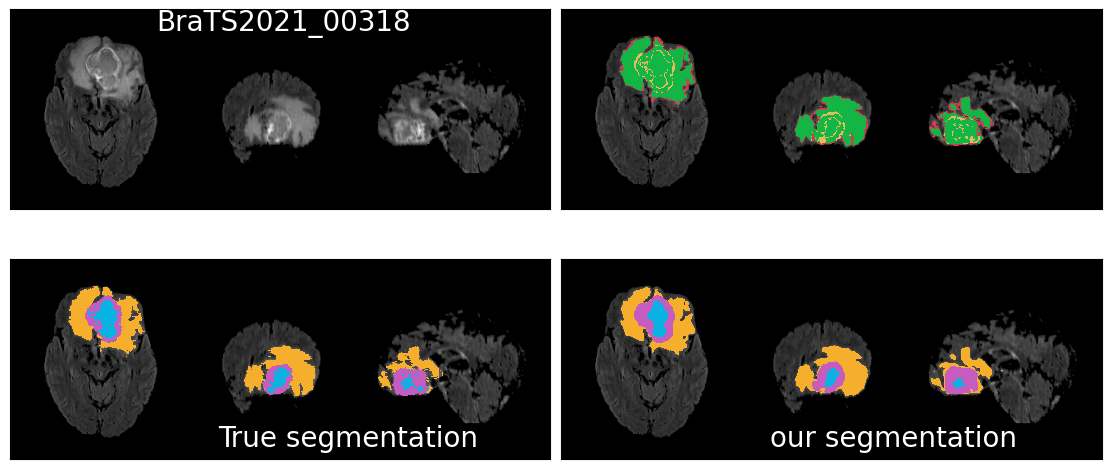
Results
& Perspective


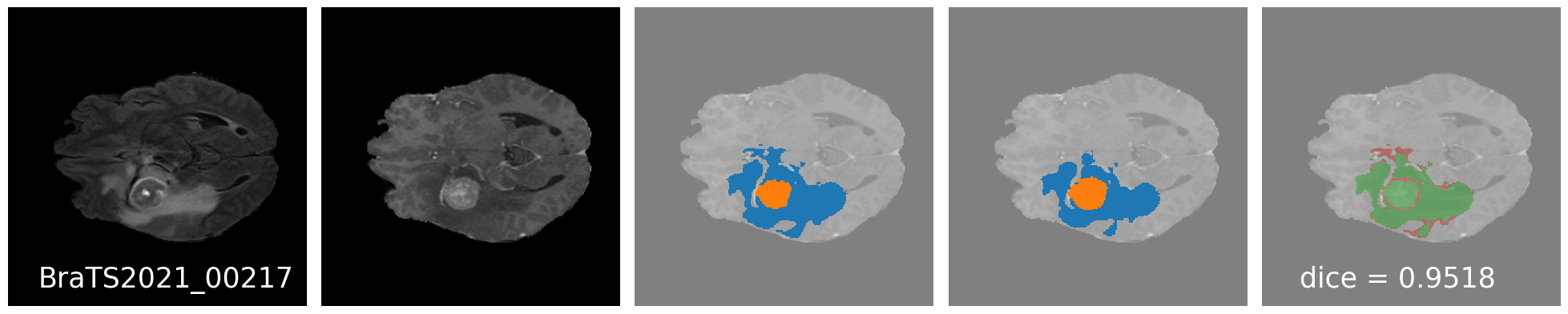


Qualitative Results : Good results




Qualitative results: ... and some bad results.
Quantitative Results

Ok
Bad
Quantitative Results

Ok
Ok
Bad
Better
Database proportion :
298/1250 images : 0.238
Perspectives
- Better parameter fine tuning
- Initial image blurring
- Step 1: threshold
- Edges detection
- Better pre-processing (normalisation, etc.)
- Make a more complex model
- Study the Gliomas topology with TDA
- Design a statistical method for model selection
- Couple with U-net
- Very good results
- Poor applicability
- Poor portability on unseen data
- Use four modalities (when usually not available in practice)
Conclusion

Does not depend on statistical tools, learning etc.,
while being no match to recent Unets
A too simple model that performs well
Take home message:
Come and check our Github:



GUDHI