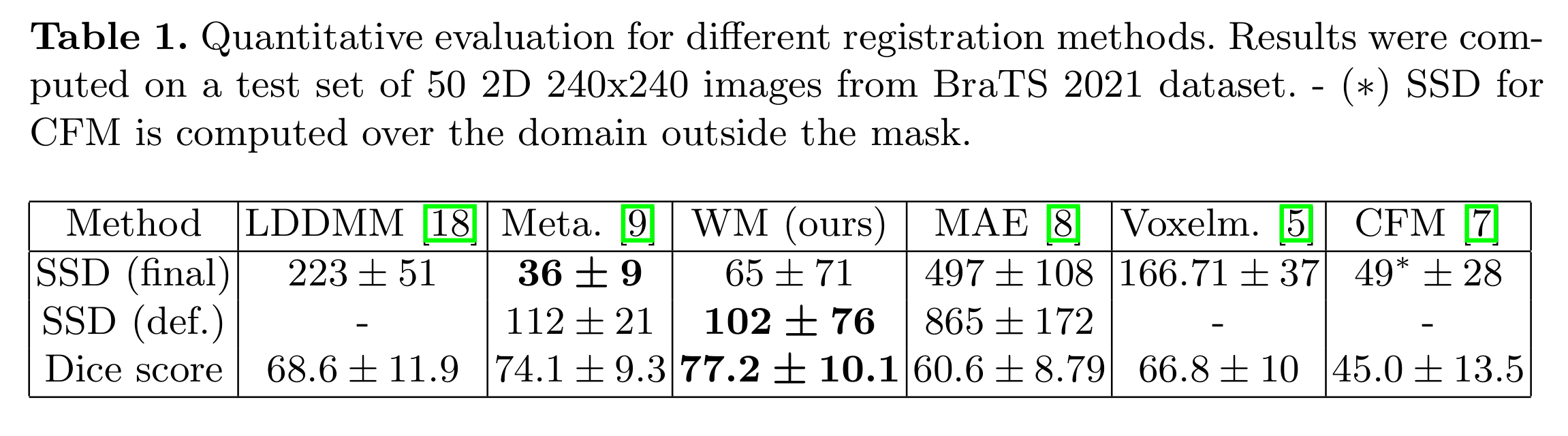
Weighted Metamorphosis

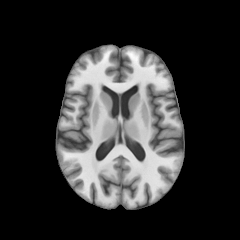
The Registration Problem

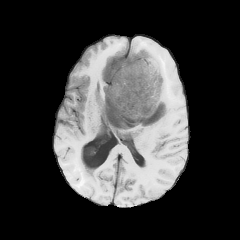
The Registration Problem

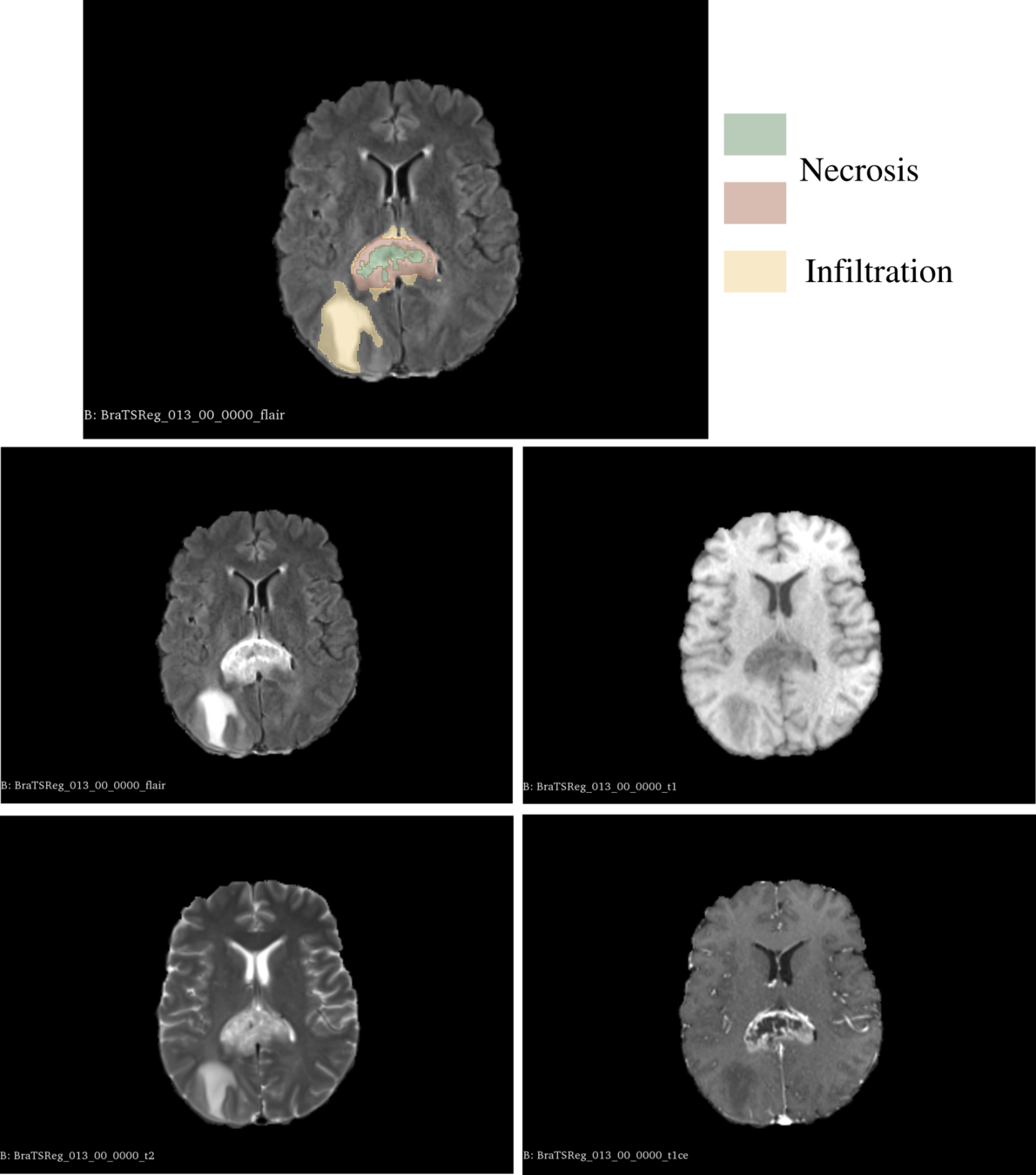
• Necrosis : topological difference
• Mass effect : morphological difference
• Oedema : appearance difference 
• Brain natural differences

MNI template

The Registration Problem

Metamorphosis & LDDMM

We aim at finding \( (v_t)_{t\in [0,1]}\) and \( (z_t)_{t \in [0,1]}\) which minimise

$$ E(I,v) = \frac 12 \| I_1 - T \|_{L^2}^2 + Reg(\bullet)$$

$$\quad s.t.: \dot I_t = -\langle \nabla I_t, v_t \rangle + \mu z_t, \quad I_0 = S, \mu \in \mathbb R^+$$

LDDMM : Register objects with the help of diffeomorphic deformations inducing a metric between images.

Metamorphosis & LDDMM

$$\left\{\begin{array}{rl}v_t &= -\frac{\rho}{\mu} K_\sigma \star  (z_t \nabla I_t)\\ \dot z_t &= -\quad \nabla \cdot (z_t v_t)  \\ \dot I_t &= -\langle v_t , \nabla I_t\rangle + \mu z_t\end{array}\right.$$

Advection equation

Continuity equation

To find the minimum of this cost :
$$ E_\mathrm M (I,v) = \frac12 \left\| I_1 - T \right\|_2^2 + \frac12\int_0^1 \|v_t\|_V^2 + \rho \|z_t\|_{L_2}^2  dt $$
We do geodesic shooting, integrating over this set of geodesic equations :

Source

Target

LDDMM

Weighted Metamorphosis

$$\left\{\begin{array}{rl}v_t &= -\frac{\rho}{\mu} K_\sigma \star  (z_t \nabla I_t)\\ \dot z_t &= -\quad \nabla \cdot (z_t v_t)  \\ \dot I_t &= -\langle v_t , \nabla I_t\rangle + \mu M_t z_t\end{array}\right.$$

Let \((M_t)_{t\in [0,1]}\) be a continuous temporal mask.

To find the minimum of this cost :
$$ E_{\mathrm{WM}}(I,v) = \frac12 \left\| I_1 - T \right\|_2^2 + \frac12\int_0^1 \|v_t\|_V^2 + \rho \langle z_t, M_t z_t \rangle_{L^2}  dt $$
We have to integrate over the set of geodesic equations :

Source

Target

LDDMM

Weighted Metamorphosis

with a growing mask.

1. We set \(M_1\) as the topological difference segmentation.

2. We initialise \(M_0\) as a small ball at its center.

3. We register \(M_0\) to \(M_1\) using LDDMM.

Source

Target

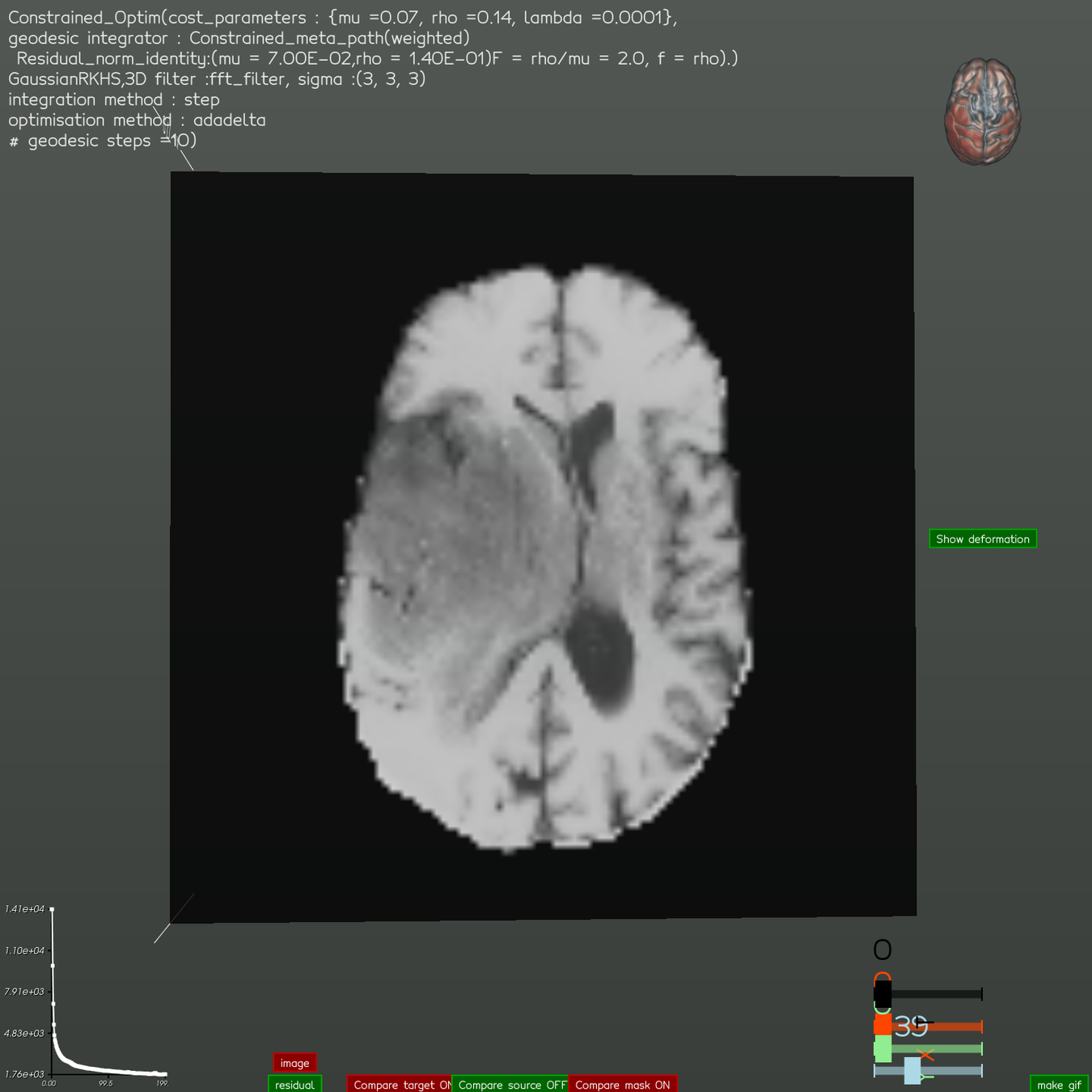
Real data :

Results in 3D

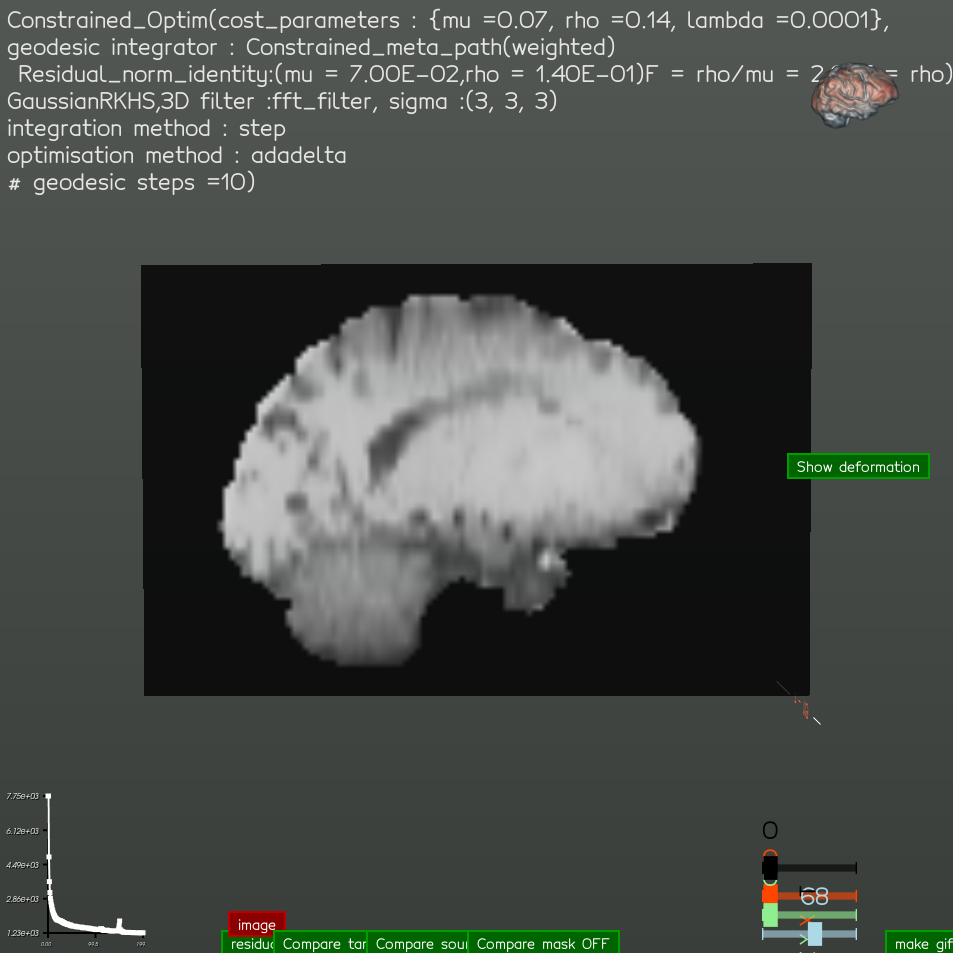
Target

Target