Plotly Visualization with Python

Alexandre Sobolevski

Armin Taheri

Today we will ...
+ Introduce plotly
+ Setup Ipython notebook
+ Example: Remake LIGO's static plots
+ Example: Scatter plot on a globe
+ Talk about our collaboration platform
+ Example: Heat Maps
+ Example: 3D Surfaces
+ Example: Quiver Plots
+ Example: Streaming API
+ Example: Mandelbrot in 3D!

why and how

we use it

is the collaboration platform for modern data science

APIs

https://plot.ly/r

https://plot.ly/python/

https://plot.ly/matlab/

https://plot.ly/js/

For This Tutorial, Let's Use

Get Started!

$ pip --version

pip 8.1.2 from /.../... (python 3.5)

Check if pip is installed

If not then install it

$ curl -O https://bootstrap.pypa.io/get-pip.py | python

$ pip --version

Some of you might need to use "sudo"

$ curl -O https://bootstrap.pypa.io/get-pip.py | sudo python

$ pip --version

Get Started!

Install Numpy, Pandas, Plotly, and Jupyter Notebook

$ pip install plotly pandas numpy jupyter

Extract and enter the tutorial notebook directory

$ tar -xvzf /path/to/plotly_tutorial.tar.gz

$ cd plotly_tutorial

$ jupyter notebook .

And you should see the notebook open in your browser!

First, We Need Some Data

Recent LIGO Paper

https://losc.ligo.org

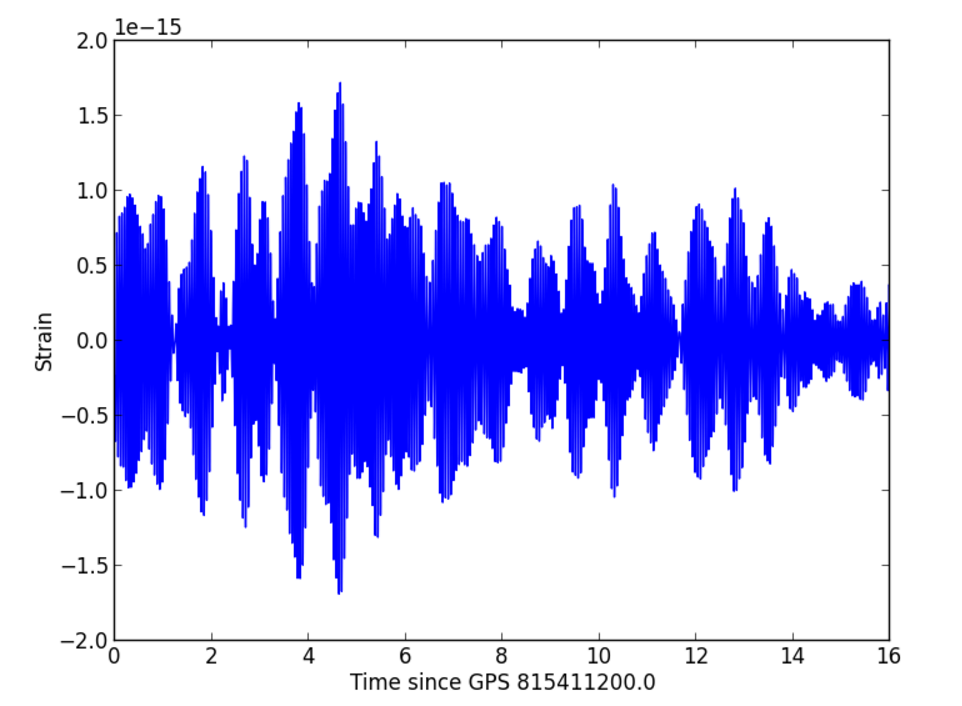
source https://losc.ligo.org

The First Reason Why We Use Plotly

Go to https://plot.ly/settings/api

and sign up if you don't have an account already.

Now you can create and save plots to the cloud inside your notebook using your API key!

https://plot.ly/organize

import plotly 

plotly.tools.set_credentials_file(
    username='tutorial.account',
    api_key='gxa2ckhtj2' #keep this a secret
)

import readligo as rl

# First from H1
strain_H1, time_H1, chan_dict_H1 = rl.loaddata(fn_H1, 'H1')
# and then from L1
strain_L1, time_L1, chan_dict_L1 = rl.loaddata(fn_L1, 'L1')

# both H1 and L1 will have the same time vector, so:
time = time_H1
delta_t = 10
indxt = np.where((time >= tevent - delta_t) & (time < tevent + delta_t))
time_seg = time[indxt] - tevent

STEP 1: DATA

STEP 2: TRACE

trace_time_series_H1 = {
    'type': 'scatter',
    'name': 'H1',
    'x': time_seg,
    'y': strain_H1
}
trace_time_series_L1 = {
    'type': 'scatter',
    'name': 'L1',
    'x': time_seg,
    'y': strain_L1
}

checkout the documentation for more options!
https://plot.ly/python/reference

layout_time_series = {
    'showlegend': True,
    'title': "LIGO strain data " + str(delta_t) + ' around of the event',
    'xaxis': {
        'title': 'time [s] since ' + str(tevent) + ' sec',
        'titlefont': {
            'family': 'Arial, monospace',
            'size': 18,
            'color': '#ff6600'
        }
    },
    'yaxis': {
        'title': '',
        'titlefont': {
            'family': 'Arial, monospace',
            'size': 18,
            'color': '#ff6600'
        }
    }
}

STEP 3: LAYOUT

STEP 4: PLOT!

import plotly.plotly as plotly
import plotly.graph_objs as go

data_time_series = go.Data([trace_time_series_H1, trace_time_series_L1])
fig_time_series = go.Figure(data = data_time_series, layout = layout_time_series)
plotly.iplot(fig_time_series, filename = 'LIGO-time-series')

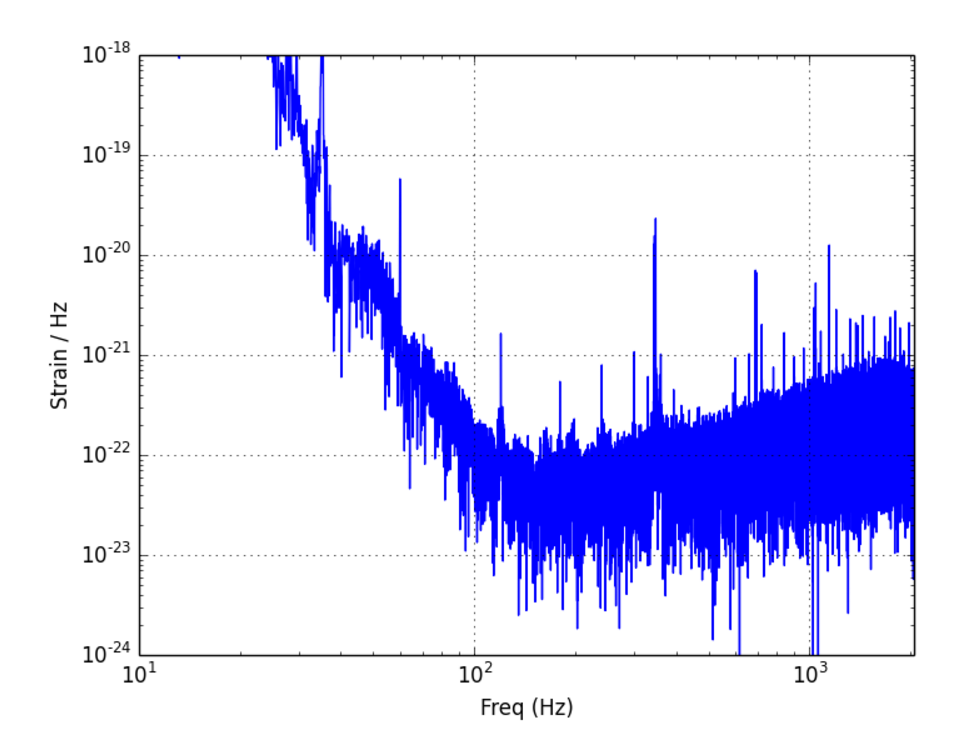
The First Reason Why We Use Plotly

t_tot = time[-1] - time[0]
dt = time[1] - time[0]
fs = int(1.0 / dt)
freq = np.arange(0, fs, 1.0/t_tot)


window = np.blackman(strain_H1.size)
windowed_strain_H1 = strain_H1*window
windowed_strain_L1 = strain_L1*window
freq_magnitude_H1 = abs(np.fft.fft(windowed_strain_H1))/t_tot
freq_magnitude_L1 = abs(np.fft.fft(windowed_strain_L1))/t_tot

STEP 1: DATA

STEP 2: TRACE

trace_fft_H1 = go.Scatter(
    name = 'H1 magnitude',
    x = freq,
    y = freq_magnitude_H1
)
trace_fft_L1 = go.Scatter(
    name = 'L1 magnitude',
    x = freq,
    y = freq_magnitude_L1
)

https://plot.ly/python/reference

layout_fft = go.Layout(
    showlegend = True,
    title = 'Strain in Frequency Domain',
    xaxis = {
        'title': 'frequency [Hz]',
        'type': 'log',
        'titlefont': {
            'family': 'Arial, monospace',
            'size': 18,
            'color': '#ff6600'
        }
    },
    yaxis = {
        'title': '$ Hz^{1/2} $',
        'type': 'log',
        'titlefont': {
            'family': 'Arial, monospace',
            'size': 18,
            'color': '#ff6600'
        }
    }
)

STEP 3: LAYOUT

STEP 4: PLOT!

import plotly.plotly as plotly
import plotly.graph_objs as go

data_fft = go.Data([trace_fft_H1, trace_fft_L1])
fig_fft = go.Figure(data = data_fft, layout = layout_fft)
plotly.iplot(fig_fft, filename = 'LIGO-frequency-distribution')

The First Reason Why We Use Plotly

Let's try something different...

latitude = [30, 46]
longitude = [-91, -119]
names = ['Livingston', 'Hanford']

STEP 1: DATA

STEP 2: TRACES

trace_location = {
    'type': 'scattergeo',
    'lat': latitude,
    'lon': longitude,
    'text': names,
    'marker': {
        'size': 10,
        'color': ['rgb(255, 0, 0)','rgb(0,0,0)']
    }
}

layout_location = {
    'title': 'Hanford and Livingston LIGO locations?',
    'geo': {
        'projection': {
            'type': 'orthographic'
        }
    }       
}

STEP 3: LAYOUT

data_location = go.Data([trace_location])
figure_location = go.Figure(data = data_location, layout = layout_location)
plotly.iplot(figure_location, filename = 'LIGO-locations')

STEP 4: PLOT!