Imagerie de diffusion

Arnaud Boré - Mars 2016 et 2017

Image structurelle

100 Milliards de neurones

Image structurelle

Principe de la diffusion

Mouvement Brownien

[Einstein 1905]

la diffusion est affectée par la structure

Diffusion dans le cerveau

Mouvement de la molécule H 0 diminué perpendiculairement à l'orientation des fibres.

L'eau diffuse plus facilement le long des fibres.

\text{}_{2}\text{}

\text{}_{2}\text{}

Diffusion orientée

Anisotropie / Isotropie des tissus

Mouvement

Isotrope

Mouvement

Anisotrope

=

=

=

=

Diffusion:

\vec{g}

\vec{g}

\vec{g}

\vec{g}

[Le Bihan et al 1985, 86]

Atténuation du signal

Signal de diffusion: valeur de b

b = 1000 s/mm

b = 2000 s/mm

b = 3000 s/mm

2

2

2

[Le Bihan et al 1985, 86]

\vec{g}

\vec{g}

S(\mathbf{b}) = S_0 e^{-\mathbf{b}ADC}

S(\mathbf{b}) = S_0 e^{-\mathbf{b}ADC}

ADC: Apparent Diffusion Coefficient

Méthodes

de reconstruction

du signal de diffusion

All models are wrong but some are usefull

Georges E. P. Box

Estimation du tenseur de diffusion

S(\mathbf{b}) = S_0 e^{-\mathbf{b}ADC}

S(\mathbf{b}) = S_0 e^{-\mathbf{b}ADC}

S(\mathbf{b}) = S_0 e^{-\mathbf{bg^TDg}}

S(\mathbf{b}) = S_0 e^{-\mathbf{bg^TDg}}

[Basser et al 1994]

D = \begin{pmatrix} D_{xx} & D_{xy} & D_{xz} \\ 0 & D_{yy} & D_{yz} \\ 0 & 0 & D_{zz}\end{pmatrix}

D = \begin{pmatrix} D_{xx} & D_{xy} & D_{xz} \\ 0 & D_{yy} & D_{yz} \\ 0 & 0 & D_{zz}\end{pmatrix}

Matrice symétrique définie positive

Reconstruire le tenseur de diffusion

6 directions de diffusion
1 image non pondérée en diffusion

Reconstruction du tenseur de diffusion

xy

xz

yz

xy

-xz

y-z

Durée de l'aquisition: 1 à 2 minutes

Propriétés du tenseur de diffusion

D = \begin{pmatrix} D_{xx} & D_{xy} & D_{xz} \\ 0 & D_{yy} & D_{yz} \\ 0 & 0 & D_{zz}\end{pmatrix}

D = \begin{pmatrix} D_{xx} & D_{xy} & D_{xz} \\ 0 & D_{yy} & D_{yz} \\ 0 & 0 & D_{zz}\end{pmatrix}

\lambda_1\vec{e}_1

\lambda_1\vec{e}_1

\lambda_2\vec{e}_2

\lambda_2\vec{e}_2

\lambda_3\vec{e}_3

\lambda_3\vec{e}_3

D = \lambda_1\vec{e}_1 + \lambda_2\vec{e}_2 +\lambda_3\vec{e}_3

D = \lambda_1\vec{e}_1 + \lambda_2\vec{e}_2 +\lambda_3\vec{e}_3

ADC = \frac{\lambda_1 + \lambda_2+\lambda_3}{3}

ADC = \frac{\lambda_1 + \lambda_2+\lambda_3}{3}

AD = \lambda_1

AD = \lambda_1

RD = \frac{\lambda_1 + \lambda_2}{2}

RD = \frac{\lambda_1 + \lambda_2}{2}

FA = \sqrt{\frac{3}{2}} \sqrt{\frac{(\lambda_1-\bar{\lambda})^2+(\lambda_2-\bar{\lambda})^2+(\lambda_3-\bar{\lambda})^2}{\lambda_1^2+\lambda_2^2+\lambda_3^2}}

FA = \sqrt{\frac{3}{2}} \sqrt{\frac{(\lambda_1-\bar{\lambda})^2+(\lambda_2-\bar{\lambda})^2+(\lambda_3-\bar{\lambda})^2}{\lambda_1^2+\lambda_2^2+\lambda_3^2}}

[Pierpaoli & Basser 96], [Pajevic & Pierpaoli 99], [Westin et al 02]

Tenseur

Interprétation des métriques

Tractographie: idée générale

[Mori et al 99], [Basser et al 00], [Tournier et al 11]

Problèmes soulevés par la tractographie

Problèmes soulevés par la tractographie

Initialisation
- Utilisation d'un masque
Critères d'arrêt et de propagation
- Angle
- Valeur de la FA
Modèle utilisé
- Tenseur trop simple

Solutions proposées

- Initialisation -

Interface GM/WM

Mask WM

Région d'intérêt

[Côté M-A et al 12, 13]

Les limites du tenseur

Profile du tenseur

Distribution de fibres avec croisement

Les limites du tenseur

J.Campbell PhD Thesis

Limité dans les croisements
Limité dans les courbures

Fantôme biologique

Attenuation du signal

\frac{S(\mathbf{q})}{S_0} = \int_{\Re^3 }P(\mathbf{r})e^{-2\pi i \mathbf{q}^T\mathbf{r}}d\mathbf{r} = \mathscr{F}[P](\mathbf{q})

\frac{S(\mathbf{q})}{S_0} = \int_{\Re^3 }P(\mathbf{r})e^{-2\pi i \mathbf{q}^T\mathbf{r}}d\mathbf{r} = \mathscr{F}[P](\mathbf{q})

[Stejskal and Tanner 1965],[Callaghan 91]

S(\mathbf{q})

S(\mathbf{q})

S(\mathbf{q})\text{: Signal de diffusion}

S(\mathbf{q})\text{: Signal de diffusion}

P(\mathbf{r})

P(\mathbf{r})

P(\mathbf{r})\text{: Propagateur de diffusion}

P(\mathbf{r})\text{: Propagateur de diffusion}

Multiplication du nombre d'acquisitions

Acquisition extrêmement demandante

60 tranches de 2mm
Plusieurs centaines de directions
10 valeurs de b entre 0 et 8000 s/mm

2

Diffusion Spectrum Imaging

\frac{S(\mathbf{q})}{S_0} = \int_{\Re^3 }P(\mathbf{r})e^{-2\pi i \mathbf{q}^T\mathbf{r}}d\mathbf{r} = \mathscr{F}[P](\mathbf{q})

\frac{S(\mathbf{q})}{S_0} = \int_{\Re^3 }P(\mathbf{r})e^{-2\pi i \mathbf{q}^T\mathbf{r}}d\mathbf{r} = \mathscr{F}[P](\mathbf{q})

Orientation Distribution Function

\text{ODF}(\theta,\phi) = \int_{0}^{\infty} P(r, \theta,\phi)r^2dr

\text{ODF}(\theta,\phi) = \int_{0}^{\infty} P(r, \theta,\phi)r^2dr

L'ODF est la projection de la densité de probabilité sur la sphère

[Tuch 02]

Orientation Distribution Function

High Angular Resolution Diffusion Imaging

162 Points

252 Points

N directions de diffusion pour une seule valeur de b

Orientation Distribution Function

\vec{g}

\vec{g}

DIFFUSION

=

ATTENUATION DU SIGNAL

Validation de l'ODF sur un fantôme

Fantôme biologique

ODFs de diffusion

Maximas

[Descoteaux et al MRM 07]

Validation de l'ODF sur un fantôme

Déconvolution sphérique

Response function

Fiber ODF

Signal de diffusion

[Tournier et al 04, 07]

Méthodes de reconstruction

Croisement: 90 degrés

ODF

[Tuch02],[Descoteaux08]

ODF-CSA

[Aganj09],[Tristan-Vega10]

fODF

[Tournier07],[Descoteaux09]

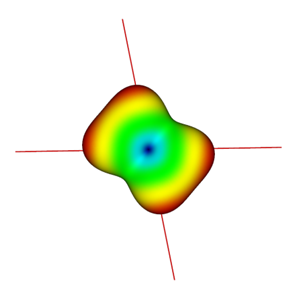
Croisement: 80 degrés

ODF

[Tuch02],[Descoteaux08]

ODF-CSA

[Aganj09],[Tristan-Vega10]

fODF

[Tournier07],[Descoteaux09]

Méthodes de reconstruction

Croisement: 70 degrés

ODF

[Tuch02],[Descoteaux08]

ODF-CSA

[Aganj09],[Tristan-Vega10]

fODF

[Tournier07],[Descoteaux09]

Méthodes de reconstruction

Différentes méthodes de reconstruction

Métriques associées

Orientation Anisotropy from fODF amplitude

- Apparent fiber density (AFD)

- Hindered Modulated Orientation Anisotropy (HMOA)

Number of fibers orientation

- NuFO

[Raffelt 12]

[Dell'Acqua 12]

Tractographies probabilistes

La tractographie deterministe assume une bonne extraction des orientations

Don't: trust tractography

Do: use prior knowledge

?

W

M

Q

L

?

? Tractométrie ?

Cousineau, M., et al "Tract-profiling and bundle statistics: a test-retest validation study." ISMRM, Singapore (2016).

Future

DSI (Sparse)
NODDI
G-ratio

Imagerie de diffusion Arnaud Boré - Mars 2016 et 2017

Made with Slides.com BESbswyBESbswyBESbswyBESbswy