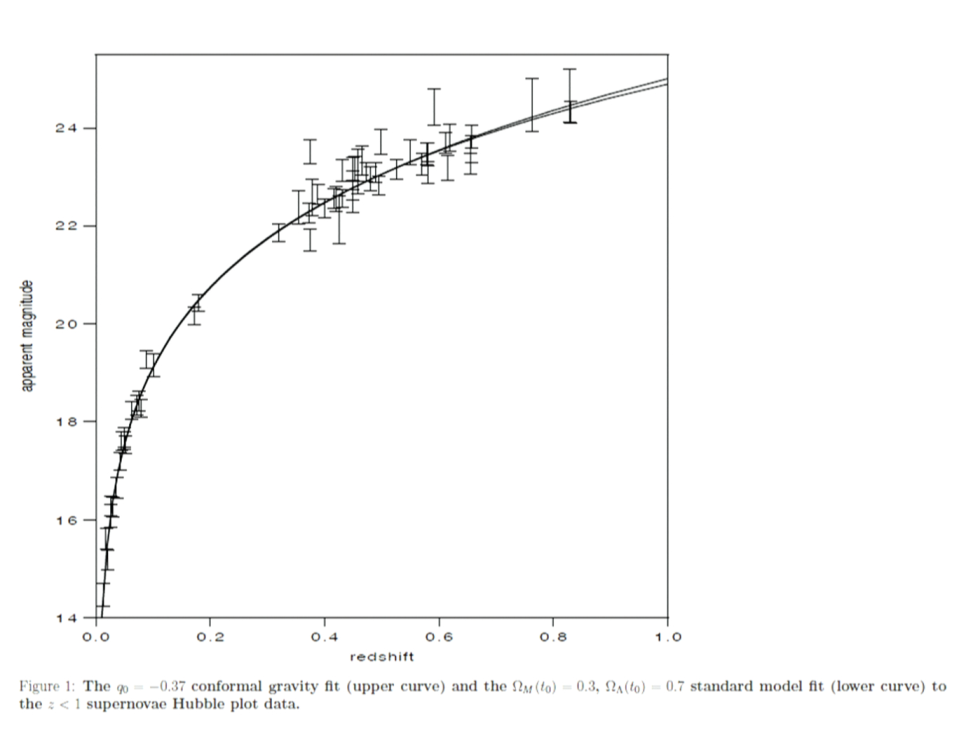
Einstein's gravity

What must be kept

\begin{aligned} &\blacktriangleright \Gamma_{\nu \sigma}^\mu &\text{ ( Christoffel symbols) }\\ &\blacktriangleright \frac{d^2 x^\mu}{ds^2} + \Gamma_{\nu\sigma}^\mu \frac{dx^\nu}{ds}\frac{dx^\sigma }{ds} = 0 &\text{ (Geodesic equation)}\\ &\blacktriangleright R_{\mu \nu \kappa}^\lambda & \text{ (Riemann tensor )}\\ &\blacktriangleright ds^2 = -B(r)dt^2 + A(r)dr^2 + r^2 d\theta^2 + r^2\sin^2\theta d \phi^2 & \text{ (Schwarzschild solution) } \end{aligned}

Einstein's gravity

What can we change

Einstein-Hilbert action

Schwarzschild solution and its Newtonian limit

That is also why we are free to add a ~Λ term

I_\text{EH} = -\frac{1}{16\pi G} \int d^4 x \; \sqrt{-g} \; R^\alpha_{\;\;\alpha}

Einstein's gravity

Problems

-\frac{1}{8\pi G}\left(R^{\mu\nu} - \frac{1}{2}g^{\mu\nu}R^{\alpha}_{\;\;\alpha}\right) = T_M^{\mu\nu}

Einstein's equations

Work very well in Solar System scales, but when we extrapolate to:

  • Galactic scales            ---> Dark Matter problem.
  • Cosmological scales ---> Dark Energy / Λ problem.
  • Strong gravity             ---> Singularities.
  • Quantization               ---> Not renormalizable.

Weyl / Conformal transformation

g_{\mu\nu} \longrightarrow e^{2 \alpha(x)} g_{\mu\nu}(x)

The EH action is not invariant under this transformation,

however there is unique action given by

I_\text{W} = -\alpha_g \int d^4 x \; \sqrt{-g}\; C_{\lambda\mu\nu\kappa} C^{\lambda\mu\nu\kappa}

which is conformally invariant.

Why should we care about Weyl invariance?

Supose we have a free massless fermion

\psi(x)

Imposing invariance under local phase transformations,

\mathcal L = (\partial^\mu \psi)^\dag (\partial_{\mu} \psi)
D_\mu = \partial_\mu + ieA_\mu(x)

Covariant derivative

"Photon"

gives us electromagnetism.

\psi \longrightarrow e^{i\alpha(x)} \psi(x)

Why should we care about Weyl invariance?

Similarly, if we ask the theory to be invariant under local coordinate transformations,

\psi \longrightarrow e^{i \omega_{\mu\nu}(x) M^{\mu\nu}} \psi(x)

Lorentz transformation

we then need a new field,

\Gamma(x)

, which gives us local Weyl invariance for free!

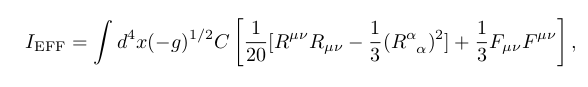
If we then evaluate Feynman's path integral, the effective action is

Conformal gravity action !

Now, what happens if we have a massive fermion?

Standard Model

If we ignore the mass ( i.e. Higgs field), then the Standard Model is conformally invariant.

However, mass and length scale break conformal invariance. The mass is generated through the dynamics of the Higgs field

V(\phi) = -\mu^2 | \phi |^2 + \lambda | \phi | ^4

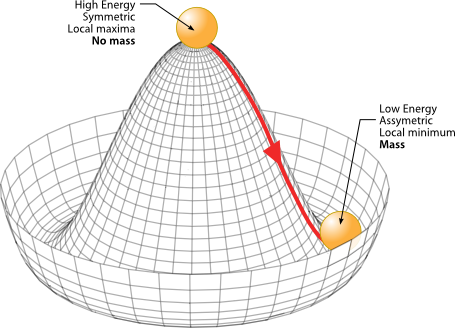
Conformal gravity

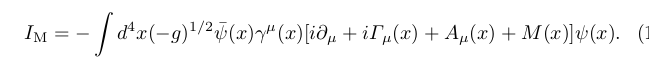
path integral formalism again...

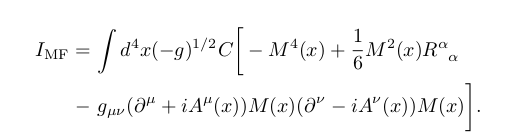
We get a Higgs potential with the Ricci scalar being the one thats gives it the Mexican hat shape!

Quantization

I_\text{W} = -\alpha_g \int d^4 x \; \sqrt{-g}\; C_{\lambda\mu\nu\kappa} C^{\lambda\mu\nu\kappa}

Unitless ----> Theory is renormalizable

Quantization

If gravity is quantized, then

T_{\mu\nu} = T^{\mu\nu}_\text{matter} + T^{\mu\nu}_\text{gravity}

So the vacuum solution is no longer

T^{\mu\nu}_\text{matter} = 0
T_{\mu\nu} = T^{\mu\nu}_\text{matter} + T^{\mu\nu}_\text{gravity} = 0

but rather

Quantization

Dark matter

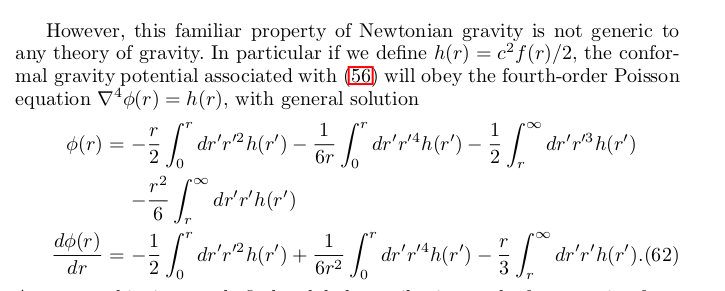
This integrates the entire Universe.

Dark matter

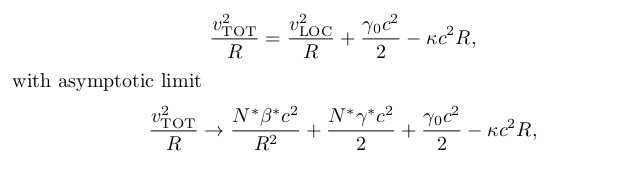
Value given by the Solar System

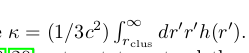
Contribution from the whole universe

Dark matter

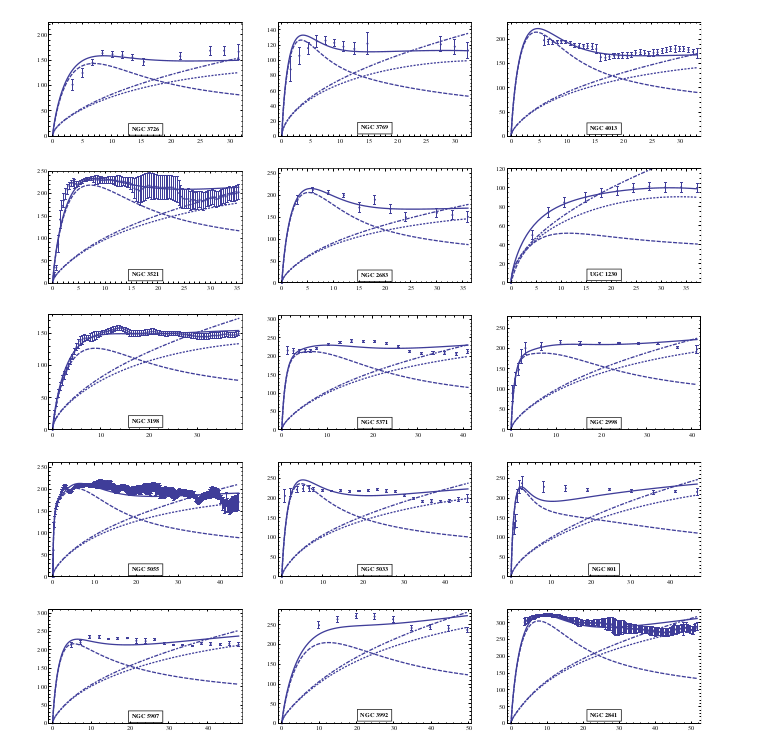
138 galaxies fitted with two free parameters.

Dark energy

Made with Slides.com