Differentiable
agent-based epidemiology
Arnau Quera-Bofarull
How to speed-up JUNE by 10,000x
Personal update


Currently postdoc at the Large Agent Collider project.
Working on the calibration of ABMs.
PIs: Ani Calinescu, Doyne Farmer, and Michael Wooldridge,
Colaborating with Ayush Chopra (MIT)
Why is JUNE slow
Object-oriented programming
class Person:
def __init__(self, age, sex):
self.age = age
self.sex = sex
self.susceptibility = 1.0
self.infectivity = 0.0In JUNE we write:
Problems:
- Functions are called millions of times
- No vectorization
Tensorization
import torch
age = torch.tensor([10, 20, 30])
sex = torch.tensor([0, 1, 0])
susceptibility = torch.tensor([1.,1.,1.])
infectivity = torch.tensor([0.,0.,0.])Idea: Use ML frameworks (PyTorch) to code ABMs
Advantages:
- Vectorized
- Code runs on GPU, for free
Tensorization
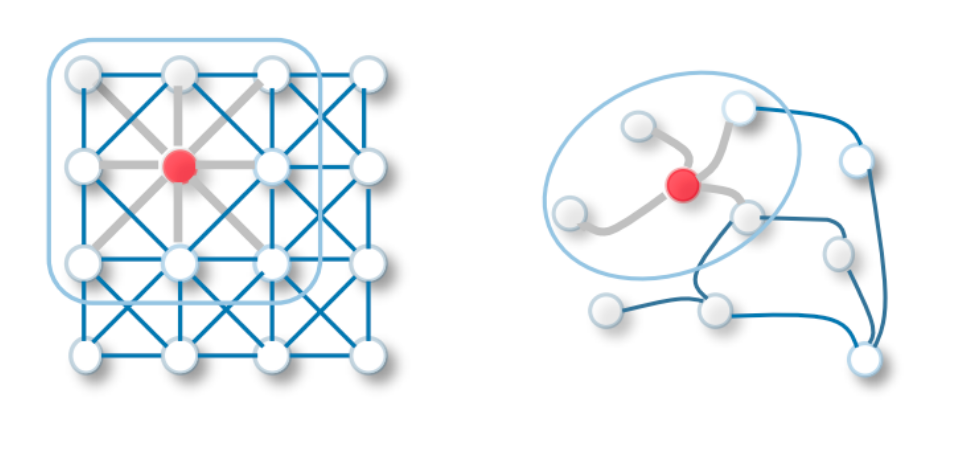
How do we implement interactions?
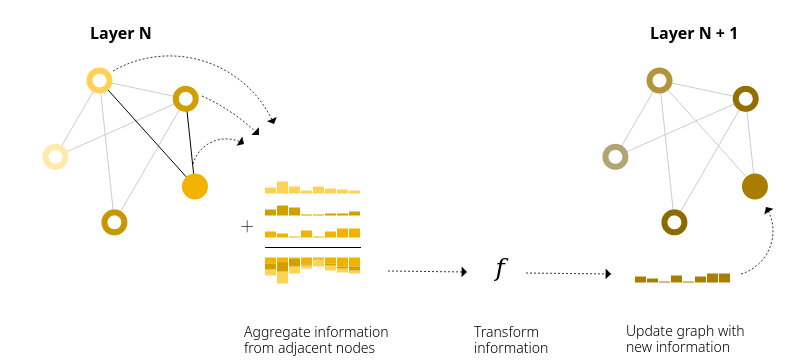
Idea: Represent JUNE as a heterogenous graph
Tensorization
Use tools for Graph Neural Networks (PyTorch Geometric)
Message Passing
Node
Edge
Message
Convolution
"Average" Message
Updated node
Updated edge
Convolution
Update node function
Update edge function
JUNE interaction in a graph
JUNE
O(100) CPU hours
Torch JUNE
O(10) CPU seconds
Differentiation
Automatic differentiation
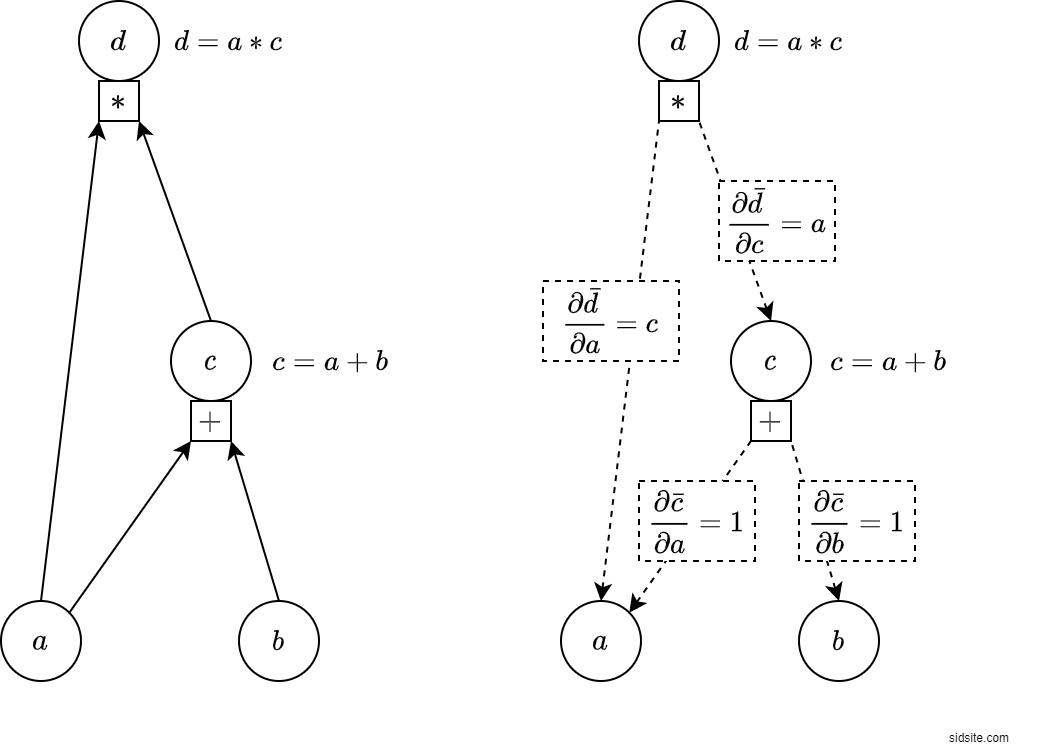
How to efficiently and reliably calculate the derivative of a program?
PyTorch supports automatic differentiation
Automatic differentiation
Problem: ABMs have discrete behaviour,
but ML people deal with this too!
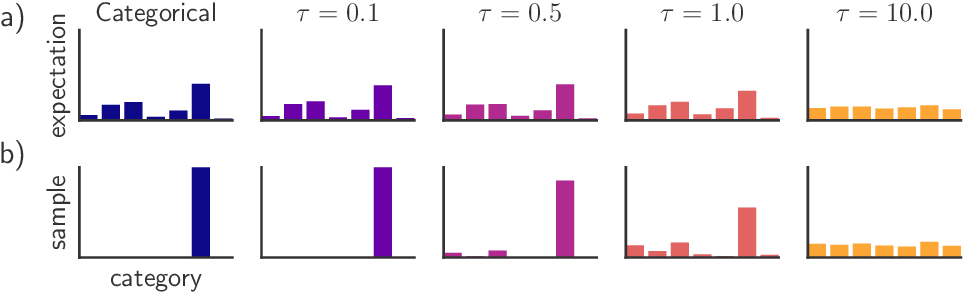
Solution: Reparametrize discrete distributions with Gumbel-Softmax trick
Automatic differentiation
We can now very efficiently calculate gradients of the type
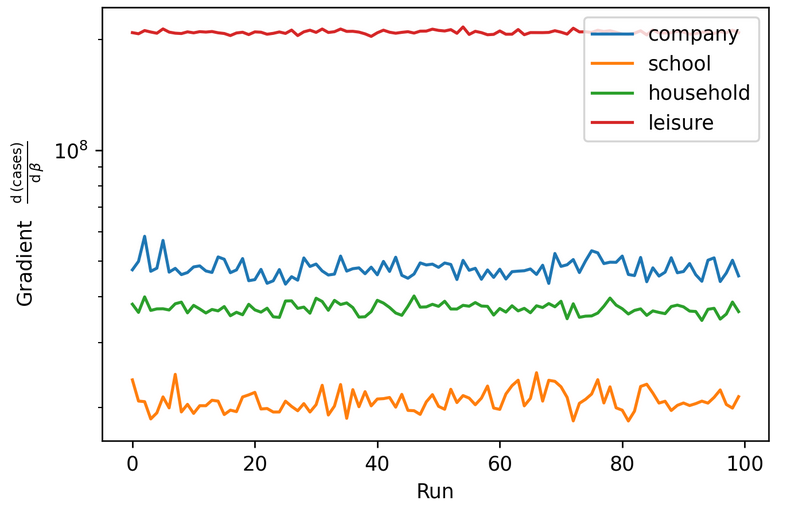
So we can fit the model using gradient descent!
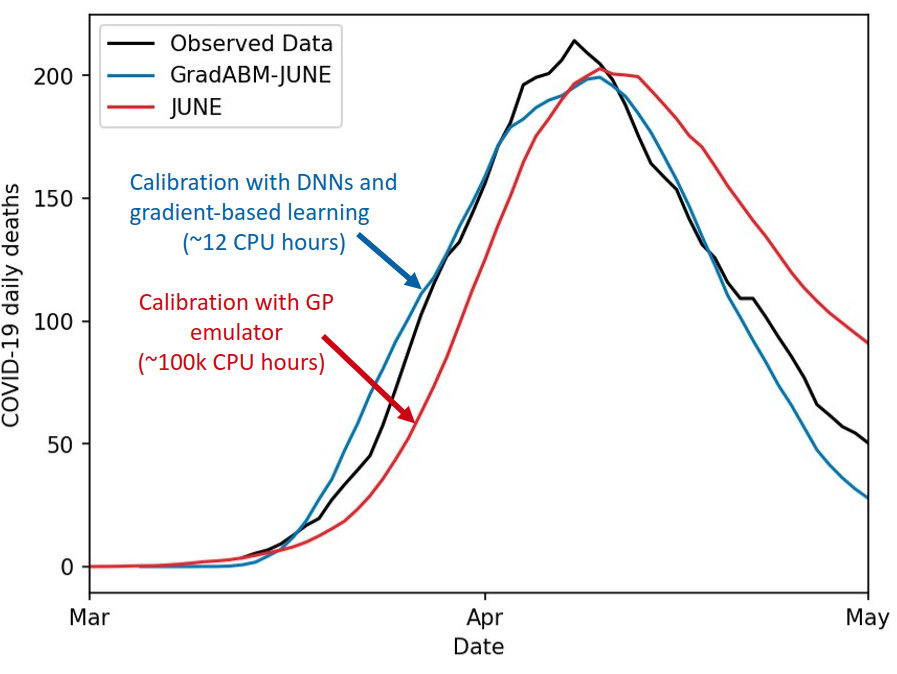
Calibration of JUNE using gradient descent
Caution:
- Not a Bayesian calibration (Work In Progress)
One-shot sensitivity analysis
Idea: Gradients give you the sensitivity
Run the simulation once, get the sensitivity for free!
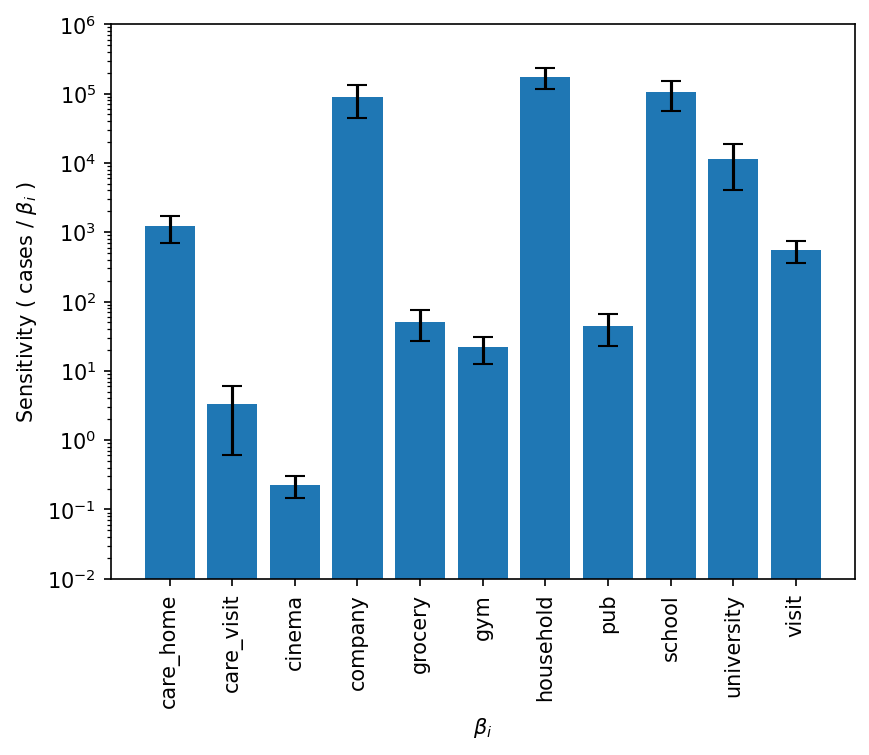
One-shot sensitivity analysis
Use this to study ABM dynamics
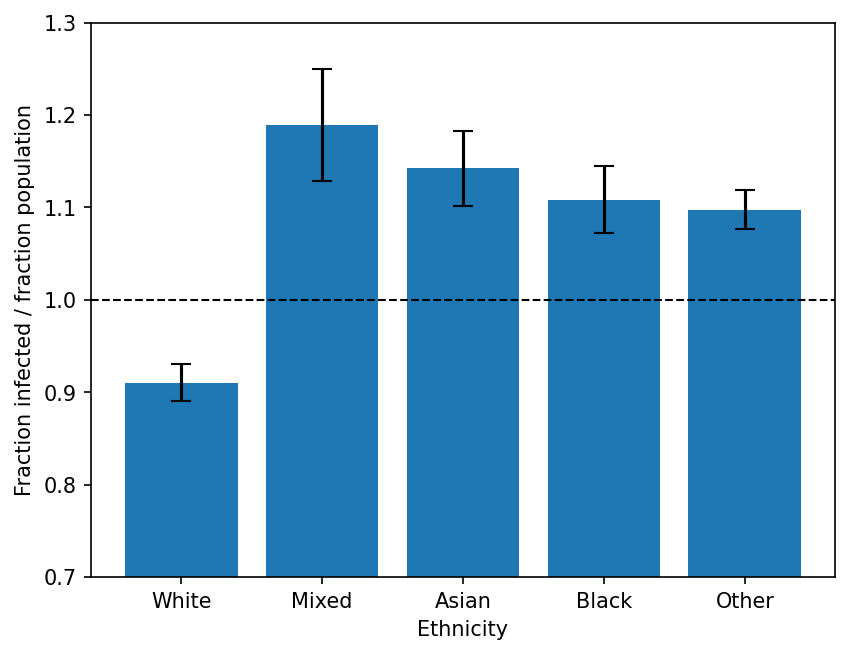
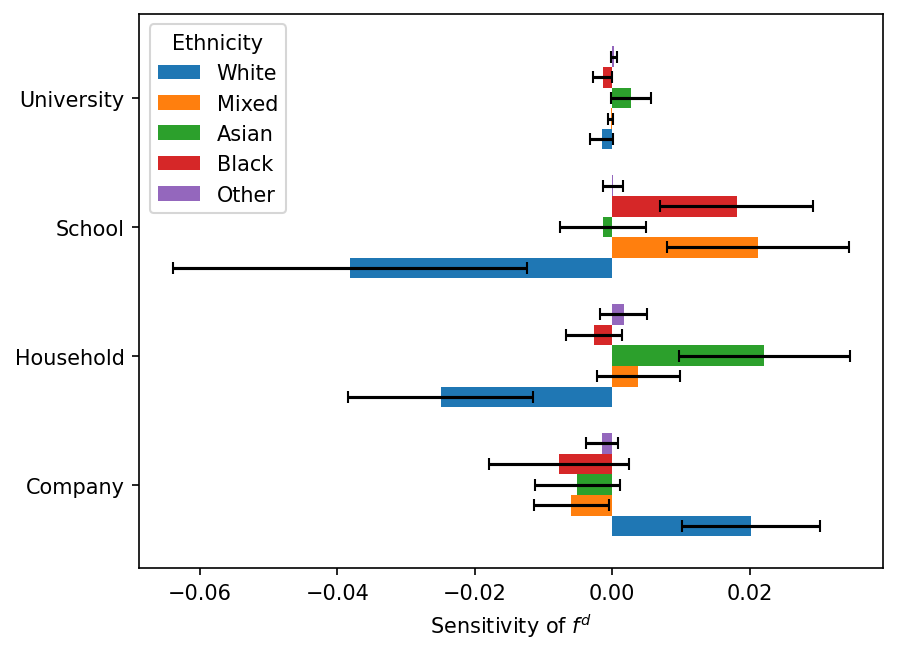
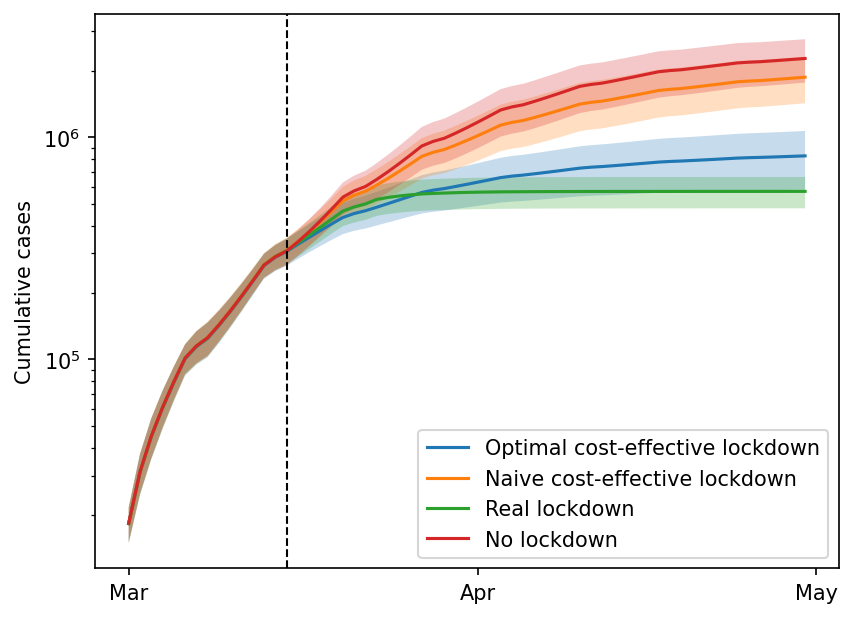
Cost-effective policy design

Gradients inform you about optimal (local) policy
Conclusions and future work
- Tensorization massively speeds up ABM simulation.
- Differentiation of ABMs possible using ML techniques.
- Gradients enable one-shot sensitivity analysis and optimal policy design.
Papers:
(Chopra et al. 2022) :
https://arxiv.org/abs/2207.09714
(Quera-Bofarull et al. 2022):
Submitted