淺入淺出貪心算法

Intro to Greedy Algorithm

Arvin Liu

前言

簡言之，貪心=通靈

~~好，我們下課~~

前言

我是麻瓜，不會通靈

增加你的~~靈力，~~靈感
背常見套路
數學證明
亂猜一通 → 如果你猜到了，其實這就是通靈

選擇類貪心

找零問題 - Change-making Problem

選擇類貪心

簡單上來說就是有 n 個物品，

你會從裡面挑幾個 (沒有順序) 當成是最佳解。

你寫過中的題目哪些是這樣的呢？

找硬幣問題：

給你一個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

通常這類的題目通常
一開始可以選個具有「最佳性質」的選項開始選。

Coin Change (leetcode 322)

給你一個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

舉例來說：

台灣有 [1, 5, 10, 50, 100, 500, 1000]
- 如果你要找給別人 261 塊你會怎麼做？
- ~~1+1+1+1+1+1+1+1+1+1+1+1+1~~
- 100 + 100 + 50 + 10 + 1
- 也就是優先使用大面額

Coin Change (leetcode 322)

但考慮比較奇怪的 case：

某個外國有的面額為 [1, 4, 5]
- 如果你要找給別人 8 塊你會怎麼做？
- 噴掉了QQ

給你一個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

回憶一下遞迴樹

f(8)

5 + f(3)

4 + f(4)

1 + f(7)

5 + 1 + f(2)

4 + 4

4 + 1 + f(3)

5 + 1 + 1 + f(1)

4 + 1 + 1 + f(2)

1 + 5 + f(2)

1 + 4 + f(3)

1 + 1 + f(6)

1 + 5 + 1 + f(1)

1 + 4 + 1 + f(2)

1 + 1 + 5 + f(1)

給你一個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

回憶一下遞迴樹

f(8)

5 + f(3)

4 + f(4)

1 + f(7)

5 + 1 + f(2)

4 + 4

4 + 1 + f(3)

1 + 5 + f(2)

1 + 4 + f(3)

1 + 1 + f(6)

給你一個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

這種類型的題目，大部分

會使用 DP 求解

f(n) = 1 + \min_{C_i \le n} f(n-C_i)

不過如果面額長得像

台灣的面額一樣的話...

回憶一下遞迴樹

f(12)

10 + f(2)

5 + f(7)

1 + f(11)

5 + 1 + f(1)

5 + 5 + f(2)

5 + 1 + f(6)

1 + 10 + f(1)

1 + 5 + f(6)

1 + 1 + f(10)

給你一個國家的面額種類，

請問最少可以用多少個硬幣湊出 amount？

不過如果面額長得像

台灣的面額一樣的話...

你會發現優先
使用最大面額

一定會拿到最佳解

你找的到一條規則可以走到最佳解，這就是

貪心法。

使用時機

在動態規劃的課程中，

我們說問題如果具有兩個性質，

那麼它就適合動態規劃 (DP)

最佳子結構

講人話就是這個大問題可以透過小問題解決。

重複子問題

講人話就是解決大問題時，小問題被問不只一次。

overlapping subproblems

optimal substructure

找零問題中，答案可以暴搜一開始選的硬幣+遞迴解決

找零問題中，遞迴時會發現每個問題有可能被問很多次

使用時機

在貪心演算法的課程中，

我們說問題如果具有兩個性質，

那麼它就適合貪心演算法 (Greedy)

最佳子結構

講人話就是這個大問題可以透過小問題解決。

optimal substructure

找零問題中，答案可以暴搜一開始選的硬幣+遞迴解決

貪婪選擇性質

講人話就是你可以在所有可能選擇到最佳解的方向。

greedy choice property

找零問題中，優先選最大面額「可能」就會是最佳解

這真的有人講中文嗎？

接下來會介紹各式各樣的貪心題，

帶你一起尋找這個所謂的「規則」。

你找的到一條規則
可以走到最佳解，這就是

貪心法

使用時機

掃描線貪心

(廣義的) Sweep-line Algorithm

掃描線演算法 sweep-line

掃描線源自於幾何題目中的算法，

例如線性規劃(LP)應該也算是掃描線？

總而言之就是隨著一條線(不一定是垂直線)移動去決定解。

凸包演算法 - Andrew's monotone chain 示意圖

*APCS不考凸包，

但學科會考喔！

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

給定 n 個區間，請算出有多少數字

被至少一個區間所覆蓋。

舉例來說，如果區間長這樣：

\{(1, 2), (5, 6), (4, 8), (7, 9)\}

那麼答案為6。因為被覆蓋的區間為

\{(1, 2), (4, 9)\} \rightarrow 2 - 1 + 9 - 4 = 6

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

給定 n 個區間，請算出有多少數字

被至少一個區間所覆蓋。

大概想像有一條掃描線，先對區間的開頭做排序，

從左往右掃就可以了。

每次都去記錄現在灰色最遠可以到哪。

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

給定 n 個區間，請算出有多少數字

被至少一個區間所覆蓋。

1. 不用管

2. 更新 cur_R

3. 從零計算

基本上你的掃描線只會遇到三種狀況。

cur_R: 灰色最遠到哪

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

給定 n 個區間，請算出有多少數字

被至少一個區間所覆蓋。

n = int(input())
L = []
for _ in range(n):
    l, r = map(int, input().split())
    L.append((l, r))
L.sort()
ans, cur_R = 0, -1
for l, r in L:
    if cur_R < l:
        cur_R = r
        ans += r - l
    elif r > cur_R:
        ans += r - cur_R
        cur_R = r
print(ans)

int n, l, r;
scanf("%d", &n);
vector<pair<int, int>> V;
while (n--){
    scanf("%d%d", &l, &r);
    V.push_back({l, r});
}
sort(V.begin(), V.end());
int ans = 0, cur_R = -1;
for (auto [l, r] : V) {
    if (cur_R < l) {
        cur_R = r;
        ans += r - l;
    }
    else if (r > cur_R) {
        ans += r - cur_R;
        cur_R = r;
    }
}
printf("%d\n", ans);

C++

Python

基本上掃描線貪心就是...

固定一個順序後，

枚舉這個順序的點去找解。

例如線段覆蓋長度就是：

順序 = 對起始做排序
枚舉灰色的起點 (區間的 l)
找出最遠到哪裡會斷掉 (區間的 r)

* 其實我不覺得掃描線是貪心，不過就...算了

最大子區間和

最大子區間和 (leetcode 53)

給定一個數列 A，請輸出子區間和最大為多少。

最大子區間和 (leetcode 53)

直觀來說，你會怎麼做？

\max_{l, r} \sum_{i=l}^{r} A_i

A = \{1,-3,4,-1,2,1,-5,4 \} % 0 1 2 3 4 5 6 7 % 1 -3 4 -1 2 1 -5 4 % % \begin{cases} A[0, 0] = 1 & = 1 \\ A[0, 2] = 1-3+4 & = 2 \\ A[0, 5] = 1-3+4-1+2+1 & = 4 \\ A[0, 7] = 1-3+4-1+2+1-5+4 &= 3 \\ A[2, 2] = 4 & = 4 \\ A[2, 5] = 4-1+2+1 &= 6 \\ A[2, 7] = 4-1+2+1-5+4 &= 5 \\ A[4, 5] = 2 + 1 &= 3 \\ A[4, 7] = 2 + 1 - 5 + 4 &= 2 \\ A[7, 7] = 4 &= 4 \\ \end{cases}

舉例來說：

有沒有一個方法在經過一些前處理後，

就可以快速的 (O(1)) 算出區間和呢？

前綴和 / 區間和

f(l, r) = \sum_{i=l}^{r} A_i = A_{l} + A_{l+1} + ... + A_{r}

prefix sum / interval (range) sum

preprocess

這是有一套標準做法的。

S[n] = \sum_{i=0}^{n} A_i

首先我們先做出這樣的陣列 (前綴和)

這件事情應該用一個迴圈就可以寫完。

S[0] = A[0];
for (int i=1; i<n; i++)
  S[i] = S[i-1] + A[i]

S = [A[0]]
for x in A[1:]:
  S.append(S[-1]+x)

C++

Python

有沒有一個方法在經過一些前處理後，

就可以快速的 (O(1)) 算出區間和呢？

前綴和 / 區間和

f(l, r) = \sum_{i=l}^{r} A_i

prefix sum / interval (range) sum

preprocess

S[n] = \sum_{i=1}^{n} A_i

我們要怎麼利用 S 還算出 f(l, r) 呢？

-(S_{l-1} = A[0] + A[1] + ... + A[l-1])

S_{r} = A[0] + A[1] + ... + A[l-1] + A[l] + A[l+1] + ... + A[r]

觀察一下...

S_{l, r} = \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,A[l] + A[l+1] + ... + A[r]

將前綴和作處理就變區間和了！

這樣我們就可以在預處理 O(n) 的情況下做到 O(1) 查詢！

給定一個數列 A，請輸出子區間和最大為多少。

最大子區間和 (leetcode 53)

\max_{l, r} \sum_{i=l}^{r} A_i

= \max_{l, r} S_{r} - S_{l-1}

回到原題，那麼就會變成這樣。

這樣要怎麼寫呢？假設我們開掃描線枚舉 r

= \max_{l, r} (S_{r} - S_{l-1}) = S_{r} + \max_{l} (- S_{l-1}) = S_{r} - \min_{l} S_{l-1}

拿 S_r 去減掉之前「最小的前綴和」

就是這個 r 最大的區間和了！

最佳解 (l^*, r^*) 的 r^* 一定會被枚舉到。\\ 所以這個方法一定會找的到最佳解

最大子區間和 (leetcode 53)

給定一個數列 A，請輸出子區間和最大為多少。

= \max_{l, r} S_{r} - S_{l-1}

\max_{l, r} \sum_{i=l}^{r} A_i

pre_sum, ans, min_sum = 0, nums[0], 0
for x in nums:
    pre_sum += x
    ans = max(ans, pre_sum - min_sum)
    min_sum = min(min_sum, pre_sum)
return ans

int pre_sum=0, min_sum=0, ans=nums[0];
for (auto x : nums) {
    pre_sum += x;
    ans = max(ans, pre_sum - min_sum);
    min_sum = min(min_sum, pre_sum);
}
return ans;

C++

Python

發現這件事情的你，其實就不用真的寫區間和啦...

拿 S_r 去減掉之前「最小的前綴和」

就是這個 r 最大的區間和了！

假設我們開掃描線枚舉 r

區間和很常考！

區間和是一個(在APCS)很常使用的技巧，

一定一定一定要好好的熟練！

可能哪天你就會突然碰到區間和的公式

(尤其遞迴 / 動態規劃)，

這個時候你就要回憶起來！

你知道線段樹嗎？

有個笑話：

有人線段樹寫到魔征，

比賽看到區間和用線段樹還不自知

最大周長三角形

Largest Perimeter Triangle (leetcode 976)

給 n 根長棍，你可以任選其中三根
組成的三角形，

那麼你可以組成的三角形中，
周長最大可以是多少。

(如果不能組成任何三角形，輸出0)

最大周長三角形 (leetcode 976)

直觀來說，你會怎麼做？

解貪心的第一件事情就是：通靈

如果你沒有想法的話...

給 n 個長棍，請找出可以組成的三角形中，

周長最大可以是多少。

(如果不能組成任何三角形，輸出0)

最大周長三角形 (leetcode 976)

考量每根棍子當 c ，怎麼選 a, b 呢？

形成三角形的條件是什麼呢？

找 a, b 比 c 小，並且這個 a, b 是最大的，

如果可以組成，

那就是選這根棍子當 c 的最大周長三角形

對於三個邊長 :

a \le b \le c

a + b > c

最大周長三角形 (leetcode 976)

sort(nums.begin(), nums.end());
while (nums.size() >= 3) {
    int n = nums.size();
    if (nums[n-1] < nums[n-2] + nums[n-3])
        return nums[n-1] + nums[n-2] + nums[n-3];
    nums.pop_back();
}
return 0;

nums.sort()
while len(nums) >= 3:
    if nums[-1] < nums[-2] + nums[-3]:
        return nums[-1] + nums[-2] + nums[-3]
    nums.pop()
return 0

C++

Python

考量每根棍子當 c ，怎麼選 a, b 呢？

找 a, b 比 c 小，並且這個 a, b 是最大的，

對於三個邊長 :

a \le b \le c

a + b > c

掃描線 + 對半拆解

Maximum Sum of 3 Non-Overlapping Subarrays (leetcode 689)

基本上遇到兩個 / 三個都是搜尋左右

class Solution:
    def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
        dp = defaultdict(lambda: (0, None))
        PS = list(accumulate(nums))
        IS = lambda L, R: PS[R] - (PS[L-1] if L>0 else 0)

        IS_k = [0] * len(nums)
        for i in range(len(nums)-k+1):
            IS_k[i] = IS(i, i+k-1)
        pre = [(-IS_k[0], 0)]
        for i in range(1, len(nums)):
            pre.append(min(pre[-1], (-IS_k[i], i)))
        suf = [(inf, len(nums)-k)]
        for i in range(len(nums)-2, -1, -1):
            suf.append(min(suf[-1], (-IS_k[i], i)))
        suf = suf[::-1]

        ans = (math.inf, None)
        for mid in range(k, len(nums)-k):
            val = IS_k[mid] - pre[mid-k][0] - suf[mid+k][0]
            pair = (pre[mid-k][1], mid, suf[mid+k][1])
            ans = min(ans, (-val, pair))
        
        return ans[1]

生產線 - Part 1

生產線 (APCS 2021/11 - 3, zj g597)

有 $n$ 台機器，每台機器生產一份資料需要 $t$ 單位時間。
這些機器需要被放置在位置 $[1, n]$ ，每個位置只能放一台機器。

有 $m$ 個任務，每個任務指定一個範圍 $[l, r]$ ，
要求範圍內的每台機器都生產 $w$ 份資料。

請問完成所有任務的最小總時間是多少？

舉例來說：

直觀來說，你會怎麼做？

🖥️D

🖥️A

🖥️B

🖥️C

🖥️E

要求0秒

要求1秒

要求2秒

要求3秒

要求0秒

答案=1+2+3=6

🖥️A 1

🖥️B 2

🖥️C 3

🖥️D 4

🖥️E 5

產生一單位
需要的秒數

任務：範圍 [2,4] 要求 1 單位

生產線 (APCS 2021/11 - 3, zj g597)

預先處理一下，先算出每個位置各需要多少資料吧！

怎麼做呢？

已經算完的

正在算的

紀錄掃描線有多少 w

還沒算完的

掃描線！

有 $n$ 台機器，每台機器生產一份資料需要 $t$ 單位時間。
這些機器需要被放置在位置 $[1, n]$ ，每個位置只能放一台機器。

有 $m$ 個任務，每個任務指定一個範圍 $[l, r]$ ，
要求範圍內的每台機器都生產 $w$ 份資料。

請問完成所有任務的最小總時間是多少？

生產線 (APCS 2021/11 - 3, zj g597)

[l, r, w]

紀錄掃描線有多少 w

掃描線！

每經過一個任務 (掃描線 = l) 就 + w
怎麼 O(1) 處理 r 的時候 - w 呢？
1. 再開一個掃描線！紀錄什麼時候要多扣誰！
  - 其實就等於兩個前綴和相減
2. 或者開一個 counting table 在 r 的位置扣掉就好了。

預先處理一下，先算出每個位置各需要多少資料吧！

生產線 (APCS 2021/11 - 3, zj g597)

預先處理一下，先算出每個位置各需要多少資料吧！

再開一個掃描線！紀錄什麼時候要多扣誰！

[l, r, w]

[l, ∞, w]

紀錄之後要-多少 w

[r+1, ∞, -w]

紅色(的前綴和) - 橘色(的前綴和) 就是你的答案。

紀錄掃描線有 + 多少 w

生產線 (APCS 2021/11 - 3, zj g597)

預先處理一下，先算出每個位置各需要多少資料吧！

再開一個掃描線！紀錄什麼時候要多扣誰！

橘色(的前綴和) - 紅色(的前綴和) 就是你的答案。

from itertools import accumulate
n, m = map(int, input().split())
work = []
needs = [0] * n
for _ in range(m):
    l, r, w = map(int, input().split())
    needs[l-1] += w
    if r != n:
        needs[r] -= w
needs = list(accumulate(needs))

Python

int n, m;
scanf("%d%d", &n, &m);
vector<int> table(n), needs(n);
for (int i=0; i<m; i++) {
  int l, r, w;
  scanf("%d%d%d", &l, &r, &w);
  table[l-1] += w;
  if (r!=n)
    table[r] -= w;
}
// 內建的前綴和，需要
// #include <numeric>
partial_sum(table.begin(), 
  table.end(), needs.begin());

C++

生產線 (APCS 2021/11 - 3, zj g597)

預先處理一下，先算出每個位置各需要多少資料吧！

真的做掃描線，然後開一個 counting table 在 r 的位置扣掉。

n, m = map(int, input().split())
work = []
for _ in range(m):
    l, r, w = map(int, input().split())
    work.append((l, r, w))
work.sort(reverse=True)
needs = [0] * (n+2)
minus = [0] * (n+2)
cur = 0
for i in range(1, n+1):
    while work and work[-1][0] == i:
        l, r, w = work.pop()
        cur += w
        minus[r+1] = w
    cur -= minus[i]
    needs[i] = cur
needs = needs[1:-1]

Python

int n, m;
scanf("%d%d", &n, &m);
vector<vector<int>> works(m, vector<int>(3));
for (auto &work : works) {
    scanf("%d%d%d", &work[0], &work[1], &work[2]);
}
sort(works.begin(), works.end());

vector<int> needs(n), minus(n);
int cur_need = 0, work_ptr = 0;
for (int i=1; i<=n; i++) {
    while (work_ptr != m && works[work_ptr][0] == i) {
        auto work = works[work_ptr];
        int l = work[0], r = work[1], w = work[2];
        if (r != n)
            minus[r] += w;
        cur_need += w;
        work_ptr++;
    }
    cur_need -= minus[i-1]; 
    needs[i-1] = cur_need;
}

C++

生產線 (APCS 2021/11 - 3, zj g597)

接下來的問題變成什麼樣呢？

有 $n$ 台機器，每台機器生產一份資料需要 $t$ 單位時間。
有 $n$ 個位置，分別需要 x 份資料。

請問要怎麼放機器才可以最小化總時間？

或者寫的數學一點：

怎麼解呢？留給之後吧！

現在 A, B 各有 n 個數字，請排列 A 和 B 使得以下最小化

\sum_{i=1}^{n} A_i \times B_i

超級洗衣機

Super washing machines (leetcode 517)

現在有 n 個數字，數字代表水平面高度。

每個地方可以花 1 秒往左右擴散 1 個高度，

請問擴散到最後需要幾秒？

Super washing machines (leetcode 517)

舉例來說：

耗時 3 秒

[4, 0, 0, 0]

[3, 1, 0, 0]

[2, 1, 1, 0]

耗時 3 秒

[1, 1, 1, 1]

[2, 6, 0, 4]

[2, 5, 2, 3]

[2, 4, 3, 3]

[3, 3, 3, 3]

直觀來說，你會怎麼做？

現在有 n 個數字，數字代表水平面高度。

每個地方可以花 1 秒往左右擴散 1 個高度，

請問擴散到最後需要幾秒？

Super washing machines (leetcode 517)

前處理：

如果 (總和 / n) 除不盡，回傳 -1。

讓最後的水平面變成 0，會比較好看一點。

[4, 0, 0, 0]

[2, 6, 0, 4]

[3, -1, -1, -1]

[-1, 3, -3, 1]

現在有 n 個數字，數字代表水平面高度。

每個地方可以花 1 秒往左右擴散 1 個高度，

請問擴散到最後需要幾秒？

Super washing machines (leetcode 517)

\{L_1, L_2, L_3, L_4, L_5,...\}

如果 L1 是 4，那就代表一定花四秒往右流 4。

如果 L1 是 -4，那就代表一定花四秒往左流 4。

考慮每個點要往左往右流多少。

大概可以知道掃描線往右然後...

現在有 n 個數字，數字代表水平面高度。

每個地方可以花 1 秒往左右擴散 1 個高度，

請問擴散到最後需要幾秒？

Super washing machines (leetcode 517)

\{L_1, L_2, L_3, L_4, L_5,...\}

如果 L1+L2+L3 < 0

L4需要往左流補左邊的洞

如果流完左邊 L4 還有剩..

L4需要往右流剩下的水

\}L_4 需要花的時間

掃描線由左往右就做可以算完了！

Super washing machines (leetcode 517)

level = sum(machines) // len(machines)
if len(machines) * level != sum(machines):
    return -1
height = [machine-level for machine in machines]

ans = 0
for i in range(len(height)):
    L_flow, R_flow = 0, 0
    # 如果左邊 < 0，表示要優先流左邊
    if i and height[i-1] < 0:
        L_flow = -height[i-1]
        height[i] += height[i-1]
        # height[i-1] = 0
    # 如果還有剩下的，那麼一定往右流
    if height[i] > 0:
        R_flow = height[i]
        height[i+1] += height[i]
        # height[i] = 0
    ans = max(ans, L_flow + R_flow)
return ans

Python

int S = 0;
for (int h : machines)
    S += h;
if (S % machines.size() != 0)
    return -1;
for (int &h : machines)
    h -= S / machines.size();
int ans = 0;
for (int i=0; i<machines.size(); i++) {
    int L_flow=0, R_flow=0;
    // 如果左邊 < 0，優先流左
    if (i && machines[i-1] < 0) {
        L_flow = -machines[i-1];
        machines[i] += machines[i-1];
        // machines[i-1] = 0;
    }
    // 如果還有剩下的，那麼一定往右流
    if (machines[i] > 0) {
        R_flow = machines[i];
        machines[i+1] += machines[i];
        // machines[i] = 0;
    }
    ans = max(ans, L_flow+R_flow);
}
return ans;

C++

貪心+二分搜

基地台  (zj c575, APCS 2017/03-4)

你需要放置 k 個基地台在一維城鎮上，目標是想讓所有住家都可以被覆蓋到。

那麼請問基地台的覆蓋直徑最小可以是多少？

(所有基地台的半徑一樣，基地台可以自己設定。)

k = 1

d最低設10

k = 2

d最低設2

直徑=10

直徑=2

完全沒概念... 不妨換個角度想想？

直觀來說，你會怎麼做？

基地台 (zj c575)

放 k 個基地台，
問最小 d 多少才可以覆蓋所有住家？

放 k 個基地台，
給定直徑 d，問可不可以覆蓋所有住家？

k = 3

掃描線往右移動，讓基地台的左界卡住沒覆蓋的房子。

原本題目

簡單化題目

直觀來說，你會怎麼做？

知道了簡化版題目，要怎麼解原題呢？

時間複雜度: O(N)

基地台 (zj c575)

放 k 個基地台，
問最小 d 多少才可以覆蓋所有住家？

放 k 個基地台，
給定直徑 d，問可不可以覆蓋所有住家？

原本題目

簡單化題目

對答案作二分搜！

O(N)

O(N \log D)

d >= d^* \rightarrow T \\ d < d^* \rightarrow F

原題：
最小直徑 d* 是多少？

d = 100 怎麼樣？

T，可以涵蓋。試試看小的

d = 50 怎麼樣？

F，不能涵蓋。試試看大的

d = 75 怎麼樣？

F，不能涵蓋。試試看大的

❓

基地台 (zj c575)

n, k = map(int, input().split())
A = list(map(int, input().split()))
A.sort()

def trail(d):
    last, quota = -d-1, k
    for cur in A:
        if last + d < cur:
            if not quota:
                return False
            quota -= 1
            last = cur
    return True

L, R = 0, 10**10
while R-L != 1:
    mid = (L+R) // 2
    if trail(mid):
        R = mid
    else:
        L = mid
print(R)

#include <stdio.h>
#include <algorithm>
int ary[50001], n, k;
bool is_ok(int x){
    int last = -x-1, now_put = 0;  
    for(int i=0; i<n; i++){
        if(last + x < ary[i]){
            now_put ++;
            last = ary[i];
            if(now_put > k){
                return false;
            }
        }
    }
    return true;
}
int main(){
    scanf("%d%d", &n, &k);
    for(int i=0; i<n; i++)
        scanf("%d", &ary[i]);
    std::sort(ary, ary+n);
    int L=0, R=1000000000;
    while(R-L != 1){
        int mid = (L+R) / 2;
        if(is_ok(mid))
            R = mid;
        else
            L = mid;
    }
    printf("%d\n", R);
    return 0;
}

C++

Python

通常會把簡化版題目寫成函式，

這樣會比較好看。

基地台 (zj c575)

多描述一下單調性值就可以二分搜尋

(掃描線)貪心小小結

背景圖是 Voronoi diagram，

算出兩點的中線交集

掃描線小結

掃描線往右移動

已經算出答案，
或者已經維護好東西了

還沒算出答案，
或者東西還沒維護

掃描線就是

一步一步地隨著掃描線的移動
去維護答案。

掃描線小結

掃描線往右移動

已經算出答案，
或者已經維護好東西了

還沒算出答案，
或者東西還沒維護

最大子區間和

最小前綴和 / 現在的前綴和

還沒被算的右界

超級洗衣機

已經流完變穩定的洗衣機

還沒穩定的洗衣機

已經被覆蓋到的房子

簡化的基地台

還沒被覆蓋到的房子

貪心小小結

通靈解法

觀察題目

可能是
貪心題

想到一個
「可能對」
的解法

構造反例
Edge Case

是錯的！

找不到反例

開始寫！

通靈不出解法

數學分析

自己生測資看看

貪心小小結

貪心非常非常非常非常容易粗心錯！
因為 APCS 是 offline judge，所以
遇到貪心題一定要特別小心！
時間允許的話，證明你的做法。
這會幫助你思考演算法的腦袋(？)
遇到貪心題，想想看你曾經寫過什麼題目。
因為通常「比較難想」的貪心題都只會出經典題！

大膽假設，小心求證

順序類貪心

簡單上來說就是有 n 個物品，

你會從裡面找一個順序具有最佳解。

動態規劃通常比較難通常找順序的最佳解，
所以這類題目通常就真的要貪心或暴搜。

選擇類貪心

簡單上來說就是有 n 個物品，

你會從裡面挑幾個 (沒有順序) 當成是最佳解。

基本上選擇類貪心都會有個動態規劃解，

因為選擇類的題目動態規劃很好出。

順序類貪心

簡單上來說就是有 n 個物品，

你會從裡面找一個順序具有最佳解。

怎麼找到順序類貪心的最佳解呢？

貪心就是通靈，你通的出來就勝利。
假設 <A, B> 跟 <B, A> 的順序
- 分析一下AB跟BA得出來的解
- 你在怎麼樣的條件會選 AB 而不是 BA 呢？

接下來讓我們看看順序類貪心
的題目都長怎樣吧！

誰先晚餐 - 通靈

A. 誰先晚餐 (TIOJ 1072, NPSC 2005 高中決賽 PA)

A. 誰先晚餐 (TIOJ 1072)

現在有一堆人要點餐，每個人點的餐有「煮的時間」跟「吃的時間」。

廚師一次只能準備一個餐點，求出最後一個人吃完時的最短時間

舉例來說：

三個人點的餐點以及
要吃的時間分別是
(1, 1), (2, 2), (3, 3)
答案是 7

直觀來說，你會怎麼做？

第一個人

第二個人

第三個人

廚師

A. 誰先晚餐 (TIOJ 1072)

現在有一堆人要點餐，每個人點的餐有「煮的時間」跟「吃的時間」。

廚師一次只能準備一個餐點，求出最後一個人吃完時的最短時間

直觀來說，你會怎麼做？

1. 從準備時間最短的開始做。

因為這樣可以讓客人先吃。

3. 從吃最久的的開始做。

因為這樣可以讓廚師沒事做的時間最小

2. 從準備時間最長的開始做。

因為這樣可以優先處理掉最佔時間的

哪個是對的？
找得出反例嗎？

3. 從吃最久的的開始做。

因為這樣可以讓廚師沒事做的時間最小

A. 誰先晚餐 (TIOJ 1072)

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main(){
    int n, C, E;
    while(cin >> n && n != 0){
        vector< pair<int,int> > V;
        for(int i=0; i<n; i++){
            cin >> C >> E; 
            V.push_back({E,C});
        }
        sort(V.begin(), V.end());
        reverse(V.begin(),V.end());   
        
        int now_time = 0, ans = 0;
        for(auto [E, C] : V){
            // 紀錄現在煮多久了。
            now_time += C;
            // 算出這個客人啥時離開，並更新最大值。
            ans = max(ans, now_time + E);
        }
        cout << ans << endl;
    }
    return 0;
}

while True:
  n = int(input())
  if n == 0:
    break
  V = [] 
  for _ in range(n):
    C, E = map(int, input().split())
    V.append((E, C))
  V.sort(reverse=True)
  now_time, ans = 0, 0
  for E, C in V:
    now_time += C
    ans = max(ans, now_time + E)
  print(ans)

C++

Python

我是麻瓜...

我連想出那三個選項都有問題...

那麼我們來試試從頭推導吧！

如何構造反例?

誰先晚餐 - 數學推導 I

A. 誰先晚餐 (TIOJ 1072, NPSC 2005 高中決賽 PA)

A. 誰先晚餐 (TIOJ 1072)

給定 n 個人，每個人有 C(ook), E(at) 時間，請排出一個順序 σ，使得以下公式最小化：

\min_{\sigma} \underset{1 \le \sigma(i) \le n} {\max} \sum_{j=1}^{\sigma(i)} C_{\sigma(j)}+ E_{\sigma(j)}

我們在寫誰先晚餐，都是用猜的再驗證。

啊我就真的連一些假解都通不出來...😭

試試看數學分析吧！

A. 誰先晚餐 (TIOJ 1072)

\min \underset{1 \le i \le n} {\max} \sum_{j=1}^{i} C_i + E_i

(C_1, E_1)

(C_2, E_2)

(C_3, E_3)

(C_4, E_4)

C_1 + C_2 \\ + C_3 + E_3

C_1 + C_2 \\ + C_3 + C_4 \\ + E_4

如果交換 (2, 3)，中間差了什麼呢？

(C_1, E_1)

(C_2, E_2)

(C_3, E_3)

(C_4, E_4)

交換

C_1+E_1

C_1+C_2\\ +E_2

C_1 + C_3 \\ + C_2 + E_2

C_1 + C_3 \\ + C_2 + C_4 \\ + E_4

C_1+E_1

C_1+C_3\\ +E_3

A. 誰先晚餐 (TIOJ 1072)

C_1 +C_2 + C_3 + E_3

C_1+C_2 +E_2

C_1 +C_3 + C_2 + E_2

C_1+C_3+E_3

順序<1, 2, 3, 4>

順序<1, 3, 2, 4>

什麼樣的條件，1234 會比 1324 一樣或更好呢？

? \rightarrow \max(C_2 + E_2, C_2 + C_3 + E_3) \le \max(C_3 + E_3, C_3 + C_2 + E_2) \\

\max \begin{cases} \\ \end{cases}

? \rightarrow \text{AND} \begin{cases} \underline{C_2 + E_2} &\le \max(C_3 + E_3, C_3 + \underline{C_2 + E_2}) \rightarrow 一定True，可忽略 \\ C_2 + C_3 + E_3 &\le \max(C_3 + E_3, C_3 + C_2 + E_2) \end{cases}

A. 誰先晚餐 (TIOJ 1072)

? \rightarrow C_2 + C_3 + E_3 \le \max(C_3 + E_3, C_3 + C_2 + E_2)

? \rightarrow \underline{C_2 + C_3} + E_3 \le \underline{C_3 + C_2} + E_2 \rightarrow E_3 \le E_2

\text{1234 比 1324 好的條件:} E_3 \le E_2

\rightarrow 對 E 排序，大的放前面。

? \rightarrow C_2 + C_3 + E_3 \le \text{OR} \begin{cases} C_3 + E_3 & \rightarrow 一定 False \\ C_3 + C_2 + E_2 \end{cases}

A. 誰先晚餐 (TIOJ 1072)

最後的最後...

為什麼只需要想兩個人的case可以推到所有人的case？

只要題目是要求一個最佳順序，

都可以嘗試這樣想！

A. 誰先晚餐 (TIOJ 1072)

* 如果前面證不出來
可能是 135 排 246 排

誰先晚餐 - 數學推導 II

A. 誰先晚餐 (TIOJ 1072, NPSC 2005 高中決賽 PA)

第二種證明 (Optional)

A. 誰先晚餐 (TIOJ 1072)

我們先考慮兩個人的 case，看看是否可以算出要先煮誰的
- 假設(煮的時間，等的時間) 分別為
我們就可以分出四種 Case，分別會是：

(C_1, E_1), (C_2, E_2)

第一個人吃比較久，先做第一個人
第一個人吃比較久，先做第二個人
第二個人吃比較久，先做第一個人
第二個人吃比較久，先做第二個人

A. 誰先晚餐 (TIOJ 1072)

第一個人吃比較久，先做第一個人
第一個人吃比較久，先做第二個人
第二個人吃比較久，先做第一個人
第二個人吃比較久，先做第二個人

\max(C_1+E_1, C_1+C_2+E_2)

\max(C_2+E_2, C_1+C_2+E_1)

\max(C_1+E_1, C_1+C_2+E_2)

\max(C_2+E_2, C_1+C_2+E_1)

A. 誰先晚餐 (TIOJ 1072)

第一個人吃比較久，先做第一個人
第一個人吃比較久，先做第二個人
第二個人吃比較久，先做第一個人
第二個人吃比較久，先做第二個人

\max(C_1+E_1, C_1+C_2+E_2)

C_1+C_2+E_1

C_1+C_2+E_2

\max(C_2+E_2, C_1+C_2+E_1)

\because E_1 \ge E_2 \\ \therefore \text {優先做第一個人}

\because E_2 \ge E_1 \\ \therefore \text {優先做第二個人}

優先做吃
最久的人。

物品堆疊 - 數學推導

物品堆疊(APCS 2017/10 - 4, zj c471)

(Optional)

現在有 n 個物品，每個物品有其 f 和 w，

請排出一個順序，使其以下數值越小越好：

直觀來說，你會怎麼做？

\sum_{i=1}^{n}(f_i \times \sum_{j=1}^{i-1} w_j)

(f_i, w_i) \rightarrow \{(1, 3), (2, 4), (3, 5)\}

\begin{cases} \{1, 2, 3\} \rightarrow 2 \times 3 + 3 \times (3 + 4) = 27 \\ \{1, 3, 2\} \rightarrow 3 \times 3 + 2 \times (3 + 5) = 25 \\ \{2, 1, 3\} \rightarrow 1 \times 4 + 3 \times (4 + 3) = 25 \\ \{2, 3, 1\} \rightarrow 3 \times 4 + 1 \times (4 + 5) = 21 \\ \{3, 1, 2\} \rightarrow 1 \times 5 + 2 \times (5 + 3) = 21 \\ \{3, 2, 1\} \rightarrow 2 \times 5 + 1 \times (5 + 4) = 19 \end{cases}

舉例來說：

物品堆疊  (APCS 2017/10 - 4, zj c471)

* 你可以看原題了解

f 跟 w 的意義是什麼，

如果你需要的話

現在有 n 個物品，每個物品有其 f 和 w，

請排出一個順序，使其以下數值越小越好：

直觀來說，你會怎麼做？

物品堆疊  (APCS 2017/10 - 4, zj c471)

老實說，這題要直觀想出來 + 有信心 AC

不是每個人都可以做到的，

所以我們嘗試分析看看吧！

目標是一個順序，所以像誰先晚餐一樣分析看看如果換中間的兩個物品，對答案會有什麼樣的影響

\sum_{i=1}^{n}(f_i \times \sum_{j=1}^{i-1} w_j)

\min \sum_{i=1}^{n}(f_i \times \sum_{j=1}^{i-1} w_j)

物品堆疊  (APCS 2017/10 - 4, zj c471)

(f_1, w_1)

(f_2, w_2)

(f_3, w_3)

(f_4, w_4)

f_2\times w_1

f_3 \times w_1 \\ + f_3 \times w_2

f_4 \times w_1 \\ + f_4 \times w_2 \\ + f_4 \times w_3

f_3\times w_1

f_2 \times w_1 \\ + f_2 \times w_3

f_4 \times w_1 \\ + f_4 \times w_3 \\ + f_4 \times w_2

如果交換 (2, 3)，中間差了什麼呢？

(f_1, w_1)

(f_2, w_2)

(f_3, w_3)

(f_4, w_4)

交換

物品堆疊  (APCS 2017/10 - 4, zj c471)

(f_1, w_1)

(f_2, w_2)

(f_3, w_3)

(f_4, w_4)

f_3 \times w_2

? \rightarrow

如果交換 (2, 3)，中間差了什麼呢？

(f_1, w_1)

(f_2, w_2)

(f_3, w_3)

(f_4, w_4)

交換

\rightarrow 對 \frac{w}{f} 做排序，比較小的放前面。

\min \sum_{i=1}^{n}(f_i \times \sum_{j=1}^{i-1} w_j)

什麼條件會使得 1234 比 1324 還要好呢？

f_2 \times w_3

\overset{想辦法把同個i放一邊}{\rightarrow} \frac{w_2 }{f_2} < \frac{w_3}{ f_3}

物品堆疊  (APCS 2017/10 - 4, zj c471)

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
    int n, tmp;
    scanf("%d", &n);
    vector<vector<double>> V;
    vector<double> w(n), f(n);
    for (int i=0; i<n; i++)
        scanf("%lf", &w[i]);
    for (int i=0; i<n; i++) {
        scanf("%lf", &f[i]);
        if (f[i])
            V.push_back({w[i]/f[i], w[i], f[i]});
    }
    sort(V.begin(), V.end());
    unsigned long long ans=0, pre_sum=0;
    for (auto v : V) {
        int w = v[1], f = v[2];
        ans += f * pre_sum;
        pre_sum += w;
    }
    printf("%llu\n", ans);
}

n = int(input())
w = list(map(int,input().split()))
f = list(map(int,input().split()))
l = [(w/f, w, f) for w,f in zip(w, f) if f]
l.sort()

ans, prefix = 0, 0
for _, wi, fi in l:
	ans += prefix * fi
	prefix += wi
print(ans)

C++

Python

小心如果 w, f 是 int，
w / f 也會是 int。

還有小心 int overflow。

經典題目！數字合併

Add All (zerojudge d221, UVA 10954)

我們定義兩數合併為 merge(x , y) → (x + y)，成本為 x + y。

給你一堆數字，求將所有數字合併成一個數字的最小成本。

直觀來說，你會怎麼做？

舉例來說：

現在需要合併的數字為 [1, 2, 3]

那麼答案會是 9。

cost : 3

cost : 6

Add All (zerojudge d221, UVA 10954)

我們定義兩數合併為 merge(x , y) → (x + y)，成本為 x + y。

給你一堆數字，求將所有數字合併成一個數字的最小成本。

直觀來說，你會怎麼做？

由小排到大，從一開始慢慢開始合併。

這樣好像會有點問題...?

合併完的數字要放哪裡？

由小排到大，從一開始慢慢開始合併，合併完放前面

由小排到大，從一開始慢慢開始合併，合併完放後面

Add All (zerojudge d221, UVA 10954)

由小排到大，
合併完放前面

由小排到大，
合併完放後面

考慮測資 : [2, 2, 3, 3]

Cost 4 - [(2, 2), 3, 3]
Cost 4 + 7 [(4, 3), 3]
Cost 4 + 7 + 10 [(7, 3)]

Cost 4 - [(2, 2), 3, 3]
Cost 4 + 6 [4, (3, 3)]
Cost 4 + 6 + 10 [(4, 6)]

考慮測資 : [1, 1, 3, 3]

Cost 4 - [(1, 1), 3, 3]
Cost 4 + 6 [(3, 3), 2]
Cost 4 + 6 + 8 [(6, 2)]

Cost 4 - [(1, 1), 3, 3]
Cost 4 + 5 [(2, 3), 3]
Cost 4 + 5 + 8 [(5, 3)]

但最佳解是：

不能每次都拿最小的兩個嗎？

Add All (zerojudge d221, UVA 10954)

不能每次都拿最小的兩個嗎？

Priority Queue / heapq!

每次拿最小的兩個合併，合併完丟回去 Priority Queue / heapq

不過，你會證明嗎？

非常的不太適合給高中生證明XD，見這裡

Add All (zerojudge d221, UVA 10954)

from queue import PriorityQueue
while True:
    n = int(input())
    if n == 0:
        break
    Q = PriorityQueue()
    for v in map(int, input().split()):
        Q.put(v)

    cost = 0
    while Q.qsize() > 1:
        A, B = Q.get(), Q.get()
        cost += A+B
        Q.put(A+B)
    print(cost)

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n, x;
    while (cin>>n && n != 0) {
        priority_queue<long long> Q;
        while(n--) {
            cin>>x;
            Q.push(-x);
        }
        long long ans=0, A, B;
        while (Q.size() != 1) {
            A = -Q.top(); Q.pop();
            B = -Q.top(); Q.pop();
            ans += A + B;
            Q.push(-(A + B));
        }
        cout << ans << endl;
    }
}

import heapq
while True:
    n = int(input())
    if n == 0:
        break
    Q = list(map(int, input().split()))
    heapq.heapify(Q)

    cost = 0
    while len(Q) > 1:
        A, B = heapq.heappop(Q), heapq.heappop(Q)
        cost += A+B
        heapq.heappush(Q, A+B)
    print(cost)

這其實很有用！？

我們來看看一個經典算法

霍夫曼編碼

Huffman Coding

(Optional)

現在有一堆文字，
怎麼編碼才可以讓總編碼的長度期望值最低？

Huffman Coding 霍夫曼編碼

什麼叫做編碼？

文本：

Fuwawa Mococo

字符	次數	編碼
F	1	000
U	1	001
W	2	010
A	2	011
M	1	100
O	3	101
C	2	110

000 001 010 011 010 011
100 101 110 101 110 101

經過編碼：

現在有一堆文字，
怎麼編碼才可以讓總編碼的長度最低呢？

Huffman Coding 霍夫曼編碼

不能亂編碼！會互撞！

字符	次數	編碼
F	1	0
U	1	1
W	2	10
A	2	11
M	1	100
O	3	101
C	2	110

0 1 10 11 10 11
100 101 110 101 110 101

文本：

Fuwawa Mococo

經過編碼：

0 -> F，這沒問題。

110 要看成是 UW 還是 C 呢？

Huffman Coding 霍夫曼編碼

可以把他轉成一個編碼樹，這樣就可以保證不會相撞！

字符	次數	編碼
F	1	000
U	1	001
W	2	010
A	2	011
M	1	100
O	3	101
C	2	110

開始!

現在有一堆文字，
怎麼編碼才可以讓總編碼的長度最低呢？

Huffman Coding 霍夫曼編碼

字符	次數	編碼
F	1	0000
U	1	001
W	2	010
A	2	011
M	1	0001
O	3	11
C	2	10

開始!

讓我們來換個編碼樹！

現在有一堆文字，
怎麼編碼才可以讓總編碼的長度最低呢？

Huffman Coding 霍夫曼編碼

字符	次數	編碼
F	1	0000
U	1	001
W	2	010
A	2	011
M	1	0001
O	3	11
C	2	10

文本：

Fuwawa Mococo

0000 001 010 011 010 011

0001 11 10 11 10 11

經過編碼：

原本: 36個 bit

現在: 33個 bit，更短了！

現在有一堆文字，
怎麼編碼才可以讓總編碼的長度最低呢？

Huffman Coding 霍夫曼編碼

字符	次數	編碼
F	1	0000
U	2	001
W	2	010
A	2	011
M	1	0001
O	3	11
C	2	10

你把兩個點的次數合併起來，
其實就會多花這兩個點的次數來編碼！

把 F 跟 M 合併，
就表示你會花 (F的次數) + (M的次數) 個 bit 來編碼！

這樣你知道跟合併數字的關係了嗎？

現在有一堆文字，
怎麼編碼才可以讓總編碼的長度最低呢？

更複雜的選擇貪心

背包問題但 W/V 最大化

http://poj.org/problem?id=2976
或
http://poj.org/problem?id=3111
, 排順序後貪心 + 二分搜

Optional

反悔貪心 - I

反悔貪心

如果你在選擇的過程中，發現有比較好的點！

那我就反悔！

反悔貪心

可以反悔的清單

...

❌

可以選！

選不進去！

好像可以把B換掉選C？

可以選！

❌

通常使用 priority_queue / heap
來找到「哪個最值得被換掉」。

加油站問題

Minimum Number of Refueling Stops (leetcode 871)

現在有個一維道路。你想開車到 target，但燃料有限。

所幸路上有很多加油站，每個加油站有其位置跟燃料數量。

問你最少加油幾次才可以到target？

start

target

=100

⛽

🚘

起始
10 燃料

+60 燃料

⛽

+30 燃料

⛽

+30 燃料

⛽

+40 燃料

≈

直觀來說，你會怎麼做？

Minimum Number of Refueling Stops (leetcode 871)

現在有個一維道路。你想開車到 target，但燃料有限。

所幸路上有很多加油站，每個加油站有其位置跟燃料數量。

問你最少加油幾次才可以到target？

直觀來說，你會怎麼做？

比較多油比較賺的，從最多油的開始加？

如果我們每次看到加油站的時候才決定要不要加，

好像有點困難？

從最多的燃料開始加嗎？

如果從最多燃料的加油站開始加，有沒有什麼條件呢？

Minimum Number of Refueling Stops (leetcode 871)

start

target

=100

⛽

🚘

起始
30 燃料

+60 燃料

⛽

+30 燃料

⛽

+30 燃料

⛽

+40 燃料

≈

"後悔沒有加" 的清單

🚘

走到 10，油還有剩，放 +60 到後悔清單
走到 20，油還有剩，放 +30 到後悔清單
走不到 40，拿最大的後悔清單 (+60)
走到 40，油還有剩，放+30到後悔清單
走到 60，油還有剩，放+40到後悔清單
走不到 100，拿最大的後悔清單 (+40)
最後答案為 2

⛽

+60 燃料

⛽

+30 燃料

⛽

+30 燃料

⛽

+40 燃料

用過了！

🚘

Minimum Number of Refueling Stops (leetcode 871)

priority_queue<int> Q;
stations.push_back(vector<int> {target, 0});
sort(stations.begin(), stations.end());
int reach = startFuel, used = 0;
for (auto station : stations) {
  // 如果走不到下個加油站，
  // 就從後悔清單拿到可以走到為止
  while (!Q.empty() && reach < station[0]) {
    reach += Q.top();
    used += 1;
    Q.pop();
  }
  // 已經到達target或者到不了下個加油站，結束。
  if (reach >= target || reach < station[0])
    break;
  Q.push(station[1]);
}
return reach >= target ? used : -1;

reach, used = startFuel, 0
stations.append([target, 0])
stations.sort()
# Heapq is min heap by default. 
# We need *-1 to negate values.
Q = []
for position, fuel in stations:
  # 如果走不到下個加油站，
  # 就從後悔清單拿到可以走到為止
  while Q and reach < position:
    reach += -heapq.heappop(Q)
    used += 1
    # 已經到達target或者到不了下個加油站，結束。
  if reach >= target or reach < position:
    break
  heapq.heappush(Q, -fuel)
return used if reach >= target else -1

C++

Python

IPO

IPO (leetcode 502)

現有個 n 個計畫，而你初始有 w 塊錢。

每個計劃都有其 c (花費), p (利潤)。

要啟動一個計劃需要花該計畫的 c 來額外獲得 p 塊錢。

如果最多能選 k 個計畫，最多可以賺多少錢？(不計成本)

直觀來說，你會怎麼做？

k = 2, w = 0, (c, p)\rightarrow \{ (0, 1), (1, 2), (1, 3)\}

舉例來說：

開頭必須要做 (0, 1)，

獲得1塊錢後做 (1, 3)，再獲得 3 塊，總共獲得 4 塊。

IPO (leetcode 502)

現有個 n 個計畫，而你有 w 塊錢。

每個計劃都有其 c (花費), p (利潤)。

要啟動一個計劃就需要花該計畫的 c 來獲得 p 塊錢。

如果你最多能選 k 個計畫，你最多可以賺多少錢？

你一定不會選 p < 0 的賠錢貨。

現在有 w 塊錢，你想選哪個當作第一個計畫？

你可以啟動並且賺最多錢的！

那第二個計劃要選誰呢？

一樣選你可以啟動的項目裡面最多錢的！

向反悔貪心一樣，用PQ來找範圍內最大值！

IPO (leetcode 502)

現有個 n 個計畫，而你有 w 塊錢。

每個計劃都有其 c (花費), p (利潤)。

要啟動一個計劃就需要花該計畫的 c 來獲得 p 塊錢。

如果你最多能選 k 個計畫，你最多可以賺多少錢？

k = 3, w = 0, (c, p)\rightarrow \{ (0, 1), (1, 2), (1, 3), (2, 3)\}

"後悔沒有賺" 的清單

選了！

賺1塊

(0, 1)

賺2塊

(1, 2)

賺3塊

(1, 3)

賺3塊

(2, 3)

w=0

w=1

w=4

選了！

已選擇的計畫：

(0, 1)

(1, 3)

(2, 3)

IPO (leetcode 502)

vector<pair<int, int>> V;
for (int i=0; i<profits.size(); i++)
    V.push_back({capital[i], profits[i]});
sort(V.begin(), V.end());
auto ptr = V.begin();
priority_queue<int> bucket;
for (int i=0; i<k; i++) {
    while (ptr != V.end() && w >= ptr->first) {
        auto [c, p] = *ptr;
        bucket.push(p);
        ptr++;
    }
    if (!bucket.empty()) {
        w += bucket.top();
        bucket.pop();
    }
}
return w;

L = sorted(zip(capital, profits))[::-1]
bucket = []
profit = w
for i in range(k):
    while L and profit >= L[-1][0]:
        c, p = L.pop()
        if p > 0:
            heapq.heappush(bucket, -p)
    if bucket:
        profit -= bucket[0]
        heapq.heappop(bucket)
return profit

C++

Python

IPO (leetcode 502)

現有個 n 個計畫，而你有 w 塊錢。

每個計劃都有其 c (花費), p (利潤)。

要啟動一個計劃就需要花該計畫的 c 來獲得 p 塊錢。

如果你最多能選 k 個計畫，你最多可以賺多少錢？

現在有個一維道路。你想開車到 target，但燃料有限。

所幸路上有很多加油站，每個加油站有其位置跟燃料數量。

問你最少加油幾次才可以到target？

加油站問題  (leetcode 871)

仔細想想其實這兩題根本是一樣的。

IPO (leetcode 502)

加油站問題  (leetcode 871)

仔細想想其實這兩題根本是一樣的。

一開始有 w 塊錢
要下個計畫要有足夠的錢。
賺的錢 = 計畫的利潤
每次選擇都要選賺最多的

一開始有 startFuel 單位的燃料
選下個加油站要有足夠的油。
加的油 = 加油站的燃料
每次沒油都要選擇之前最多的

限制 k 找最大利潤

限制最遠距離找最小 k

互為對偶問題，所以兩個解法一樣。

所以寫貪心記得要想想自己曾經寫過什麼喔！

IPO (leetcode 502)

真的對 C 做排序是好的嗎？來試試看推導！(補充)

<1, 2, 3, 4> \rightarrow \begin{cases} c_2 \le p_1 + w \\ c_3 \le p_1 + p_2 + w \end{cases}

<1, 3, 2, 4> \rightarrow \begin{cases} c_3 \le p_1 + w \\ c_2 \le p_1+ p_3 + w \end{cases}

1234 跟 1324 利潤一樣，1234比1324好的條件：

? \rightarrow OR \begin{cases} c_2 \le p_1 + w, c_3 \le p_1 + p_2+ w, c_3 > p_1+ w \\ c_2 \le p_1 + w, c_3 \le p_1 + p_2 + w, c_2 > p_1 + p_3 + w \end{cases}

? \rightarrow OR \begin{cases} c_2 < c_3, 0 < p_2 \rightarrow 0 < p2 一定是對的，因為如果沒賺你不會選 \\ p_2 > p_3, p_3 < 0 \rightarrow p_3 < 0 賠錢，不做 \rightarrow False \end{cases}

? \rightarrow c_2 < c_3，真的要對 c 做排序！

de morgan 定理: A&B&!(C&D) = (A&B&!C) | (A&B&!D)

順序 + 選擇型貪心

簡單上來說就是有 n 個物品，

你會從裡面挑幾個 (有順序) 當成是最佳解。

選擇類貪心

簡單上來說就是有 n 個物品，

你會從裡面挑幾個 (沒有順序) 當成是最佳解。

順序類貪心

簡單上來說就是有 n 個物品，

你會從裡面找一個順序具有最佳解。

順序+選擇類貪心

通常這類題目會先找順序，

有了順序之後再做選擇。

通常這類題目的選擇都會用反悔貪心

順序 + 選擇型貪心

簡單上來說就是有 n 個物品，

你會從裡面挑幾個 (有順序) 當成是最佳解。

順序+選擇類貪心

通常這類題目會先找順序，

有了順序之後再做選擇。

為什麼呢？假設有 n 個物品要選

假設最佳解是按照著字典序的

順序 + 選擇型貪心

那麼你先對原本 n 個物品排序

你再選擇 k 個就可以了。

不相交區間

Non-overlapping intervals (leetcode 435)

Non-overlapping Intervals (leetcode 435)

現在有一堆任務，每個任務有起始時間跟結束時間。你一次只能做一個任務，問最少需要放棄任務的數量？

直觀來說，你會怎麼做？

舉例來說：

四個任務的時間是
[1, 2], [2, 3], [3, 4],
[1, 3]
答案是 1
(把 [1, 3] 放棄)

[1, 2]

[2, 3]

[3, 4]

[1, 3]

Non-overlapping Intervals (leetcode 435)

直觀來說，你會怎麼做？

放棄任務的數量...不太好想。

換個角度想：如果是最多可以做多少任務呢？

1. 從任務所花時間最短的開始選，因為他的費時最小。

3. 從任務結束時間最早的開始做，因為早做完就可以快選下一個。

2. 從任務開始時間最早的開始做，早做完早享受。

3. 從任務結束時間最早的開始做，因為早做完就可以快選下一個。

現在有一堆任務，每個任務有起始時間跟結束時間。你一次只能做一個任務，問最少需要放棄任務的數量？

Non-overlapping Intervals (leetcode 435)

現在有一堆任務，每個任務有起始時間跟結束時間。你一次只能做一個任務，問最多可以做多少任務？

話是這麼說，但怎麼從頭分析呢？

現在有 n 個任務，已經確定這 n 個任務可以全部完成，請你給出這個任務順序。

我們先從簡單版題目來決定順序：

既然任務彼此都是不相交...
那麼對開始或對結束排序都可以吧？

接著讓我們來選原本的題目！

Non-overlapping Intervals (leetcode 435)

現在有一堆對開始時間做排序的任務表，
你一次只能做一個任務，
問最多可以做多少任務？

既然都是不相交...
那麼對開始或對結束排序都可以吧？

如果上一個任務的 E <= Si:
- 直接加。
如果上一個任務的 E > Si：
1. 可能要選 i：如果 Ei 很小，那麼選 i 比較賺！
  - 如果 Ei 比上一個任務的 Eb 還要大，那不可能選 i。
2. 如果可以一換一，那要放棄哪一個呢？
  - 顯然是你選擇的最後一個任務 (Sb, Eb)。
3. 那會不會要二換一呢？
  - 可能嗎？

Non-overlapping Intervals (leetcode 435)

現在有一堆對開始時間做排序的任務表，
你一次只能做一個任務，
問最多可以做多少任務？

[S1, E1]

[S3, E3]

對開始做排序，會不會要拿之前選的二換現在的一呢？

[S2, E2]

如果你需要二換一才可以插入 3，

那麼一定長得像上面這樣。

但是因為 S2 <= S3，

所以絕對不會二換一。

Non-overlapping Intervals (leetcode 435)

對開始做排序，對 E 做反悔貪心

// saved with (e, s)
sort(intervals.begin(), intervals.end());
priority_queue<pair<int, int>> Q;
for (auto &tmp : intervals) {
    int s=tmp[0], e=tmp[1];
    if (Q.empty() || s >= Q.top().first) {
        Q.push({e, s});
    } else if (e <= Q.top().first) {
        Q.pop();
        Q.push({e, s});
    }
}
return intervals.size() - Q.size();

C++

intervals.sort()
Q = [] # Save (-ei, si)
for s, e in intervals:
    if not Q or s >= -Q[0][0]:
        heapq.heappush(Q, (-e, s))
    elif e < -Q[0][0]:
        heapq.heappop(Q)
        heapq.heappush(Q, (-e, s))
return len(intervals) - len(Q)

Python

現在有一堆對結束時間做排序的任務表，
你一次只能做一個任務，
問最多可以做多少任務？

Non-overlapping Intervals (leetcode 435)

現在有一堆對結束時間做排序的任務表，
你一次只能做一個任務，
問最多可以做多少任務？

如果上一個任務的 E <= Si:
- 直接加。
如果上一個任務的 E > Si：
1. 可能要選 i ... 嗎？
  - 沒有，這個時候選 i 一定比較爛。
    連一換一變好的機會都沒有。
直接對 E 做排序，如果可以選就選，不能選就不選。

對結束時間做排序呢？

Non-overlapping Intervals (leetcode 435)

現在有一堆對結束時間做排序的任務表，
你一次只能做一個任務，
問最多可以做多少任務？

對結束時間做排序呢？

intervals.sort(key = lambda a: a[1])
cur_r = -float('inf')
ans = 0
for l, r in intervals:
  if cur_r <= l:
    cur_r = r
    ans += 1
return len(intervals) - ans

sort(intervals.begin(), intervals.end(), 
     [](auto &a, auto &b) {
       return a[1] < b[1];
     });
int current_end = -50000, chosen = 0;
for (auto &interval : intervals) {
  if (current_end <= interval[0]) {
    current_end = interval[1];
    chosen ++;
  }
}
return intervals.size() - chosen;

C++

Python

湖畔大樓 - Part 1

湖畔大樓(107北市賽決賽 - 2, zj e877)

現在有 n 個物品，每個物品有其 H 和 L，

請從中選出 k 個物品，排出一個順序，

使其滿足以下條件。( k 越大越好 )

i\in {[1, k]}, L_i \ge \sum_{j=1}^{i-1} H_j

湖畔大樓  (107北市賽決賽 - 2, zj e877)

* 你可以看原題了解

H 跟 L 的意義是什麼，

如果你需要的話

(H_i, L_i) \rightarrow \{(2, 5), (5, 1), (10, 7)\}

\begin{cases} \{1, \cancel {2, 3}\} \rightarrow \cancel{1 \ge 2, 7 \ge (2 + 5)} &\rightarrow 1 \\ \{1, 3, \cancel {2}\} \rightarrow 7 \ge 2, \cancel {1 \ge (2 + 10)} &\rightarrow 2 \\ \{2, 1, 3\} \rightarrow 5 \ge 5, 7 \ge (5 + 2) &\rightarrow 3\\ \{2, 3, \cancel {1}\} \rightarrow 7 \ge 5, \cancel {5 \ge (5 + 10)} &\rightarrow 2 \\ \{3, \cancel {1, 2}\} \rightarrow \cancel {5 \ge 10, 1 \ge (10 + 2)} &\rightarrow 1 \\ \{3, \cancel {2, 1}\} \rightarrow \cancel {1 \ge 10, 5 \ge (10 + 5)} &\rightarrow 1 \end{cases}

舉例來說：

直觀來說，你會怎麼做？

現在有 n 個物品，每個物品有其 H 和 L，

請從中選出 k 個物品，排出一個順序，

使其滿足以下條件。( k 越大越好 )

i\in {[1, k]}, L_i \ge \sum_{j=1}^{i-1} H_j

湖畔大樓  (107北市賽決賽 - 2, zj e877)

直觀來說，你會怎麼做？

這題直觀其實有點困難，我們先從順序開始想。

現在有 n 個物品，每個物品有其 H 和 L，

請從中選出 k 個物品，排出一個順序，

使其滿足以下條件。( k 越大越好 )

i\in {[1, k]}, L_i \ge \sum_{j=1}^{i-1} H_j

湖畔大樓  (107北市賽決賽 - 2, zj e877)

現在有 n 個物品，每個物品有其 H 和 L，

保證有一個順序可以使以下式子成立。

請找出順序。

i\in {[1, n]}, L_i \ge \sum_{j=1}^{i-1} H_j

簡化版題目：

湖畔大樓  (107北市賽決賽 - 2, zj e877)

現在有 n 個物品，每個物品有其 H 和 L，

保證有一個順序可以使以下式子成立。

請找出順序。

i\in {[1, n]}, L_i \ge \sum_{j=1}^{i-1} H_j

簡化版題目：

這種找順序問題我們好像有一套方法可以分析？

我們都是麻瓜，所以我們來試試看吧！

什麼條件下，選2會比選3還要好呢？

考慮 <1, 2, 3, 4> 跟 <1, 3, 2, 4>

i\in {[1, n]}, L_i \ge \sum_{j=1}^{i-1} H_j

湖畔大樓  (107北市賽決賽 - 2, zj e877)

(H_1, L_1)

(H_2, L_2)

(H_3, L_3)

(H_4, L_4)

(H_1, L_1)

(H_2, L_2)

(H_3, L_3)

(H_4, L_4)

交換

L_2 \ge H_1

L_3 \ge (H_1 + H_2)

L_4 \ge (H_1 + \\H_2 + H_3)

L_3 \ge H_1

L_2 \ge (H_1 + H_3)

L_4 \ge (H_1 + \\H_3 + H_2)

什麼條件下，選2會比選3還要好呢？

如果不成立，那麼也不成立，

這樣 2 跟 3 都不能選，沒什麼好比較的。

L_2 \ge H_1

L_2 \ge (H_1 + H_3)

i\in {[1, n]}, L_i \ge \sum_{j=1}^{i-1} H_j

湖畔大樓  (107北市賽決賽 - 2, zj e877)

L_3 \ge (H_1 + H_2)

L_2 \ge (H_1 + H_3)

什麼條件下，選2會比選3還要好呢？

成立

不成立

? \rightarrow L_3 \ge (H_1 + H_2) \text{ and } L_2 < (H_1 + H_3)

? \rightarrow L_3 + \underline{H_3} \ge (H_1 + H_2 + \underline{H_3}) \text{ and } L_2 + \underline{H_2} < (H_1 + \underline{H_2} + H_3)

? \rightarrow L_3 + H_3 \ge (H_1 + H_2 + H_3) > L_2 + H_2

當 L_3 + H_3 > L_2 + H_2 的時候，2要放得比3前面 \\ \rightarrow 對 H_i + L_i 排序，小的放前面

湖畔大樓  (107北市賽決賽 - 2, zj e877)

當 L_3 + H_3 > L_2 + H_2 的時候，2要放得比3前面 \\ \rightarrow 對 H_i + L_i 排序，小的放前面

我們已經找出順序了！

不過我們要怎麼解出原題呢？

如果你選了 k 個當成解答，
那麼對 H + L 排序一定可以把這 k 的按照順序放好。

怎麼挑選 k 個？

我們可以先把所有東西按照 H + L 排序後再挑！

湖畔大樓  (107北市賽決賽 - 2, zj e877)

L_2 \ge H_1

L_3 \ge (H_1 + H_2)

L_3 \ge H_1

L_2 \ge (H_1 + H_3)

補充：如果你覺得刪掉 L2 >= H1 很怪，那就不要刪試試看。

1234 比 1324 好的條件是甚麼？

成立

不成立

? \rightarrow OR \begin{cases} L_2 \ge H_1 \text{ and } L_3 \ge (H_1 + H_2) \text{ and } L_3 < H_1 \\ L_2 \ge H_1 \text{ and } L_3 \ge (H_1 + H_2) \text{ and } L_2 < (H_1 + H_3) \end{cases}

? \rightarrow OR \begin{cases} L_2 > L_3 \text{ and } 0 \ge H_2 & \rightarrow H_2 必 > 0，False \\ H_3 > 0 \text{ and } L_3 + H_3 > L_2 + H_2 & \rightarrow H_3 必 > 0，忽略 \end{cases}

你會得到一樣的結論，那就是對 L+H 排序。

湖畔大樓  (107北市賽決賽 - 2, zj e877)

湖畔大樓 - Part 2

湖畔大樓  (107北市賽決賽 - 2, zj e877)

當 L_3 + H_3 > L_2 + H_2 的時候，2要放得比3前面 \\ \rightarrow 對 H_i + L_i 排序，小的放前面

我們已經找出順序了！

不過我們要怎麼解出原題呢？

現在有 n 個物品，每個物品有其 H 和 L，

請從中選出 k 個物品，排出一個順序，

使其滿足以下條件。( k 越大越好 )

i\in {[1, k]}, L_i \ge \sum_{j=1}^{i-1} H_j

湖畔大樓  (107北市賽決賽 - 2, zj e877)

找出最大的k, 使得\, i\in {[1, k]}, L_i \ge \sum_{j=1}^{i-1} H_j

好像可以動態規劃了！

DP[n, k] = 在前n個物品中，選出k個的最小高度

怎麼定義遞迴呢？

Hint: 回憶一下 LIS 的題目吧！

DP_{n, k} = \min \begin{cases} DP_{n-1, k} \\ DP_{n-1, k-1} + H_n & \text{if } L_n \ge DP_{n-1, k-1} \end{cases}

湖畔大樓  (107北市賽決賽 - 2, zj e877)

int n, h, l;
scanf("%d", &n);
vector<pair<int, int>> V;
vector<int> DP(n+1, INT_MAX);
DP[0] = 0;
for (int i=0; i<n; i++) {
    scanf("%d%d", &h, &l);
    V.push_back({h+l, h});
}
int ans = 0;
sort(V.begin(), V.end());
for (auto [lim, h] : V) {
    for (int k=n; k>=1; k--) {
        if (DP[k-1] <= lim-h) {
            DP[k] = min(DP[k], DP[k-1] + h);
            ans = max(ans, k);
        }
    }
}
printf("%d\n", ans);

n = int(input())
L = []
for _ in range(n):
    h, l = map(int, input().split())
    L.append((h, l))

L.sort(key=lambda x: x[0] + x[1])
DP = [0] + [float('inf')] * n
ans = 0
for h, l in L:
    for k in range(n, 0, -1):
        if DP[k-1] <= l:
            DP[k] = min(DP[k], DP[k-1]+h)
            ans = max(ans, k)
print(ans)

C++

O(n^2) 會 TLE ... (但還是有90%)

有沒有其他方法呢？

Python

DP_{n, k} = \min \begin{cases} DP_{n-1, k} \\ DP_{n-1, k-1} + H_n & \text{if } L_n \ge DP_{n-1, k-1} \end{cases}

湖畔大樓  (107北市賽決賽 - 2, zj e877)

找出最大的k, 使得\, i\in {[1, k]}, L_i \ge \sum_{j=1}^{i-1} H_j

現在要加入一個 (H_i, L_i) ...

如果前面的 H 加總 ≤ Li :
- 直接加。
如果前面的 H 加總 > Li：
1. 可能要選 i：如果 Hi 很小，那麼選 i 比較賺！
2. 如果可以一換一，那要放棄哪一個呢？
  - 放棄最大的 H 的那一個，因為這會讓加總 H 比較小。
3. 那會不會要二換一呢？
  - 不會，因為
  - 既然 b 已經被放進去了，那麼 i 一定也放得進去。

H_b + L_b \le H_i + L_i \rightarrow 如果H_b > H_i，那麼 L_b < L_i

(b 是被你選的人之中 H 最高的那個)

湖畔大樓  (107北市賽決賽 - 2, zj e877)

import heapq
n = int(input())
L = []
for _ in range(n):
    l, h = map(int, input().split())
    L.append((h, l))
L.sort(key=lambda x: x[0] + x[1])

pq = []
ans, cur_h = 0, 0
for l, h in L:
    if l >= cur_h:
        cur_h += h
        heapq.heappush(pq, -h)
        ans += 1
    elif -pq[0] > h:
        cur_h += h - (-pq[0])
        heapq.heappop(pq)
        heapq.heappush(pq, -h) 
print(ans)

int n, h, l;
scanf("%d", &n);
vector<pair<int, int>> V;
for (int i=0; i<n; i++) {
    scanf("%d%d", &h, &l);
    V.push_back({h+l, h});
}
sort(V.begin(), V.end());

priority_queue<int> PQ;
int ans = 0, cur_h=0;
for (auto [lim, h] : V) {
    if (lim-h >= cur_h) {
        PQ.push(h);
        cur_h += h;
        ans += 1;
    } else if(PQ.top() > h) {
        PQ.pop();
        PQ.push(h);
        cur_h += h - PQ.top();
    }
}
printf("%d\n", ans);

C++

Python

這個貪心演算法其實叫做
Moore-Hodgson Algorithm！

甚至 2021 年有人出了一個證明論文

湖畔大樓  (107北市賽決賽 - 2, zj e877)

匹配類貪心

基本上題目都會是給你兩群東西，

請你找出誰跟誰配隊會有最佳解。

A 群

B 群

匹配類貪心

基本上題目都會是給你兩群東西，

請你找出誰跟誰配隊會有最佳解。

通常這類題目每一堆只會有一個數字，

所以通常都是兩堆先排序，

不是順著就是逆著配對。

當然也有兩個東西以上的配對，但我們沒有要教
匹配類有相關的演算法，我們只討論可以貪心的題目。

餅乾分配

Assign Cookie (leetcode 455)

現在有一堆餅乾跟一堆小孩，

餅乾有各自的「滿足度」，小孩有各自的「貪心度」。

如果小孩吃的餅乾「滿足度」大於等於自己的「貪心度」，他會很開心。

每個小孩最多只能給一片餅乾，請問你最多可以讓幾位小孩開心？

舉例來說：

有三個小孩，貪心度分別為 [1, 2, 3]
有兩個餅乾，滿足度分別為 [1, 2]
你的解答會是 2，因為 1->1, 2->2。

直觀來說，你會怎麼做？

Assign Cookie (leetcode 455)

現在有一堆餅乾跟一堆小孩，

餅乾有各自的「滿足度」，小孩有各自的「貪心度」。

如果小孩吃的餅乾「滿足度」大於等於自己的「貪心度」，他會很開心。

每個小孩最多只能給一片餅乾，請問你最多可以讓幾位小孩開心？

直觀來說，你會怎麼做？

1. 從貪心度最小的餅乾開始給，
優先滿足最不貪心的小孩。

因為不貪心的小孩最好被滿足。

2. 從貪心度最大的餅乾開始給，
優先滿足最貪心的小孩。

因為可以保證餅乾可以被
最適合的貪心小孩吃掉

Assign Cookie (leetcode 455)

1. 從貪心度最小的餅乾開始給，
優先滿足最不貪心的小孩。

g.sort(reverse=True)
s.sort(reverse=True)
ans = 0
while s and g:
  if s[-1] >= g[-1]:
    ans += 1
    del g[-1], s[-1]
  else:
    del s[-1]
return ans

都可以AC!

sort(g.rbegin(), g.rend());
sort(s.rbegin(), s.rend());
int ans = 0;
while (!s.empty() && !g.empty()) {
  if (s.back() >= g.back()) {
    ans += 1;
    s.pop_back(), g.pop_back();
  } else {
    s.pop_back();
  }
}
return ans;

C++

Python

Assign Cookie (leetcode 455)

2. 從貪心度最大的餅乾開始給，
優先滿足最貪心的小孩。

sort(g.begin(), g.end());
sort(s.begin(), s.end());
int ans = 0;
while (!s.empty() && !g.empty()) {
  if (s.back() >= g.back()) {
    ans += 1;
    s.pop_back(), g.pop_back();
  } else {
    g.pop_back();
  }
}
return ans;

都可以AC!

g.sort()
s.sort()
ans = 0
while s and g:
  if s[-1] >= g[-1]:
    ans += 1
    del g[-1], s[-1]
  else:
    del g[-1]
return ans

C++

Python

Assign Cookie (leetcode 455)

從貪心度最小的餅乾開始給，

優先滿足最不貪心的小孩。

證明：為什麼是對的？

🍪

🧒

🍪

🐷

假設小餅乾給小孩是最佳解。
如果小餅乾給更貪心的小孩 (豬)，那麼一定不會比原本的解更好。
- 你給小孩，答案是 1 + f(2, 2)
- 你給豬，答案是 1 + f(3, 2)
- f(2, 2) 顯然比 f(3, 2) 更好或一樣，因為有多一個選擇。

你能證明看看第二個方法的正確性嗎？

生產線 - Part 2

生產線 (APCS 2021/11 - 3, zj g597)

有 $n$ 台機器，每台機器生產一份資料需要 $t$ 單位時間。
這些機器需要被放置在位置 $[1, n]$ ，每個位置只能放一台機器。

有 $m$ 個任務，每個任務指定一個範圍 $[l, r]$ ，
要求範圍內的每台機器都生產 $w$ 份資料。

請問完成所有任務的總時間是多少？

舉例來說：

直觀來說，你會怎麼做？

🖥️D

🖥️A

🖥️B

🖥️C

🖥️E

要求0秒

要求1秒

要求2秒

要求3秒

要求0秒

答案=1+2+3=6

🖥️A 1

🖥️B 2

🖥️C 3

🖥️D 4

🖥️E 5

產生一單位
需要的秒數

任務：範圍 [2,4] 要求 1單位

生產線 (APCS 2021/11 - 3, zj g597)

[l, r, w]

紀錄掃描線有多少 w

掃描線！

每經過一個任務 (掃描線 = l) 就 + w
怎麼 O(1) 處理 r 的時候 - w 呢？
1. 再開一個掃描線！紀錄什麼時候要多扣誰！
  - 其實就等於兩個前綴和相減
2. 或者開一個 counting table 在 r 的位置扣掉就好了。

預先處理一下，先算出每個位置各需要多少資料吧！

生產線 (APCS 2021/11 - 3, zj g597)

接下來的問題變成什麼樣呢？

有 $n$ 台機器，每台機器生產一份資料需要 $t$ 單位時間。
有 $n$ 個位置，分別需要 x 份資料。

請問要怎麼放機器才可以最小化總時間？

或者長這樣：

怎麼解呢？

現在 A, B 各有 n 個數字，請排列 A 和 B 使得以下最小化

\sum_{i=1}^{n} A_i \times B_i

生產線 (APCS 2021/11 - 3, zj g597)

試試通靈！

感覺上應該是大的 * 小的總合會比較小。

可是我不會通靈 😭...

老樣子，試試看數學分析吧！

現在 A, B 各有 n 個數字，請排列 A 和 B 使得以下最小化

\sum_{i=1}^{n} A_i \times B_i

生產線 (APCS 2021/11 - 3, zj g597)

現在 A, B 各有 n 個數字，請排列 A 和 B 使得以下最小化

\sum_{i=1}^{n} A_i \times B_i

老樣子，試試看數學分析吧！

(A_1, B_1) (A_2, B_2) \rightarrow A_1B_1 + A_2B_2

考慮 n = 2，什麼條件下 A1 會跟 B1 配，A2 會跟 B2 配呢？

(A_1, B_2) (A_2, B_1) \rightarrow A_1B_2 + A_2B_1

? \rightarrow A_1B_1 + A_2B_2 < A_1B_2 + A_2B_1

? \rightarrow A_1(B_1-B_2) + A_2(B_2-B_1) < 0

? \rightarrow (A_1 - A_2)(B_1 - B_2) < 0

生產線 (APCS 2021/11 - 3, zj g597)

考慮 n = 2，什麼條件下 A1 會跟 B1 配，A2 會跟 B2 配呢？

? \rightarrow (A_1 - A_2)(B_1 - B_2) < 0

現在 A, B 各有 n 個數字，請排列 A 和 B 使得以下最小化

\sum_{i=1}^{n} A_i \times B_i

? \rightarrow OR \begin{cases} (A_1 - A_2) < 0 , (B_1 - B_2) > 0 \\ (A_1 - A_2) > 0 , (B_1 - B_2) < 0 \\ \end{cases}

? \rightarrow OR \begin{cases} A_1 < A_2, B_1 > B_2\\ A_1 > A_2, B_1 < B_2\\ \end{cases}

生產線 (APCS 2021/11 - 3, zj g597)

先對 A 排序應該不影響題目。

那麼 B 應該就會是反著排序，因為可以一直交換。

現在 A, B 各有 n 個數字，請排列 A 和 B 使得以下最小化

\sum_{i=1}^{n} A_i \times B_i

考慮 n = 2，什麼條件下 A1 會跟 B1 配，A2 會跟 B2 配呢？

? \rightarrow OR \begin{cases} A_1 < A_2, B_1 > B_2\\ A_1 > A_2, B_1 < B_2\\ \end{cases}

A_1 < A_2 < A_3 < ... < A_n

B_1 > B_2 > B_3 > ... > B_n

生產線 (APCS 2021/11 - 3, zj g597)

// include 省略
using namespace std;

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    vector<int> table(n), needs(n);
    for (int i=0; i<m; i++) {
        int l, r, w;
        scanf("%d%d%d", &l, &r, &w);
        table[l-1] += w;
        if (r!=n)
            table[r] -= w;
    }
    partial_sum(table.begin(), table.end(), needs.begin());

    vector<int> machines(n);
    for (int i=0; i<n; i++)
        scanf("%d", &machines[i]);

    sort(needs.rbegin(), needs.rend());
    sort(machines.begin(), machines.end());
    long long ans = 0;
    for (int i=0; i<n; i++) {
        ans += 1ULL * needs[i] * machines[i];
    }
    printf("%lld", ans);
    return 0;
}

from itertools import accumulate
n, m = map(int, input().split())
work = []
needs = [0] * n
for _ in range(m):
    l, r, w = map(int, input().split())
    needs[l-1] += w
    if r != n:
        needs[r] -= w
needs = list(accumulate(needs))

machines = list(map(int, input().split()))
machines.sort(reverse=True)
needs.sort()
ans = 0
for a, b in zip(machines ,needs):
    ans += a * b
    
print(ans)

C++

Python

反悔貪心 - II

貪心選擇，但保留後路

很難，可惜 APCS 不會考

反悔貪心 - II

如果你在選擇的過程中，發現有比較好的點！

那我就反悔！

反悔貪心 - II

在反悔貪心 I 中，我們會將直接將反悔選項
放到堆裡面，等著我們反悔。

在反悔貪心 II 中，我們無法直接將反悔選項
放到堆裡面，我們必須要事先處理反悔選項，才可以把它放進反悔堆內。

接著來讓我們看怎麼個「事先處理」吧！

接下來的兩題有點難，不過這個難度 APCS 絕對不會考 (但比賽有可能)，所以就當作課外聽聽看就好！

分Pizza

Pizza with 3n slices (leetcode 1388)

標程是 DP O(n²)，但可以貪心 O(nlogn)

Pizza with 3n slices (leetcode 1388)

有 3 $n$ 片圓形的 Pizza，每片的大小都不一樣，
要分給你，Alice 和 Bob 三個人。

你優先選擇其中一片 Pizza，Alice，Bob就會選擇你那片的兩側。
總共你會選擇 $n$ 片，此時 3 $n$ 片 Pizza 就會分完。
問你怎麼選才可以使吃到的 Pizza 最多？

舉例來說：

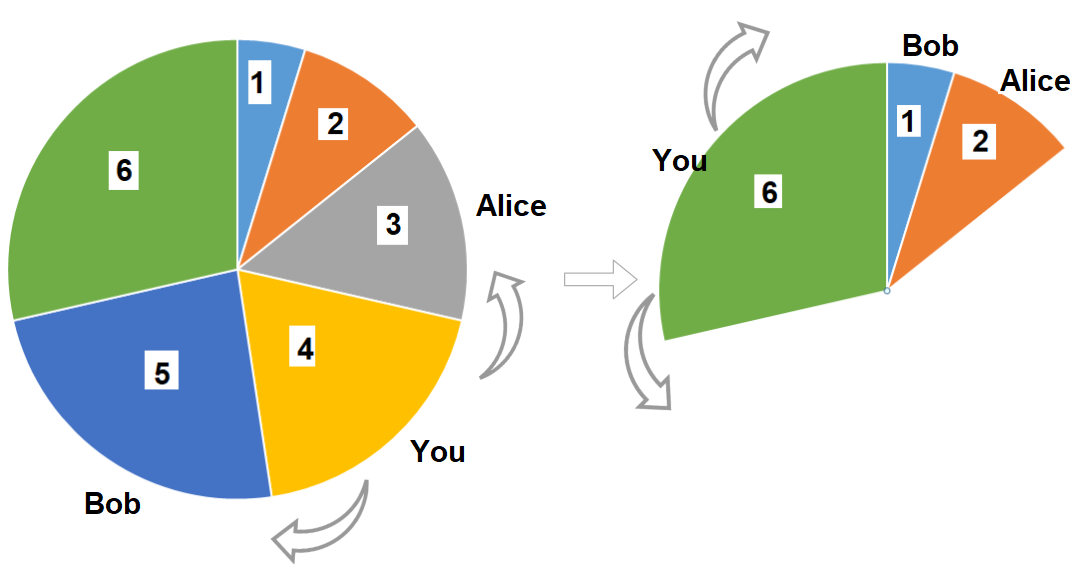
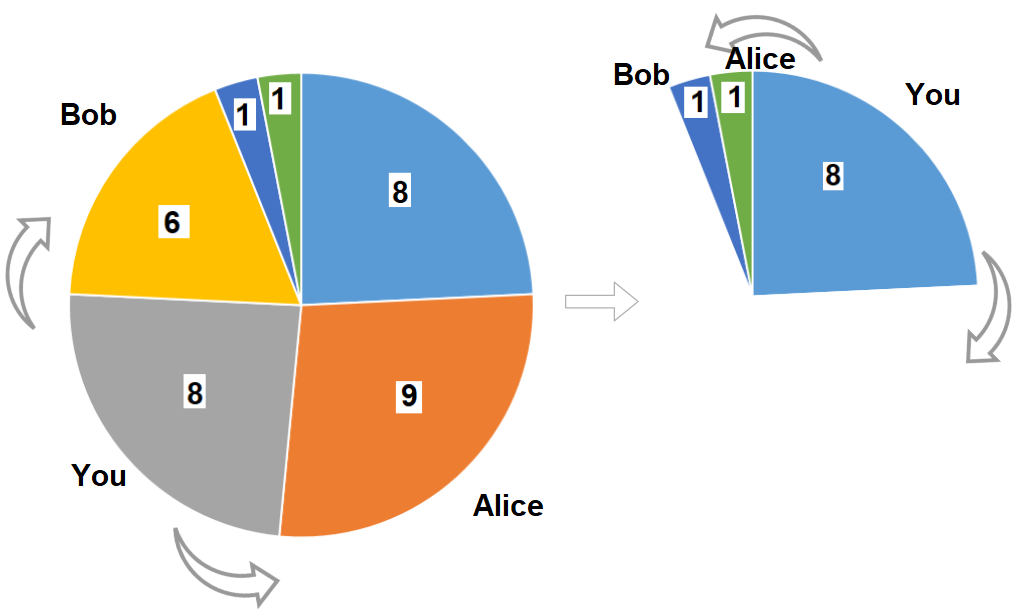
最佳解: 拿了 4 + 6 = 10

最佳解: 拿了 8 + 8 = 16

Pizza with 3n slices (leetcode 1388)

有 3 $n$ 片圓形的 Pizza，每片的大小都不一樣，
要分給你，Alice 和 Bob 三個人。

你優先選擇其中一片 Pizza，Alice，Bob就會選擇你那片的兩側。
總共你會選擇 $n$ 片，此時 3 $n$ 片 Pizza 就會分完。
問你怎麼選才可以使吃到的 Pizza 最多？

這題上本質其實就是在
一個陣列選 n 個數字，
但帶有些限制。

你覺得條件是甚麼呢？

[8, 9, 8, 6, 1, 1]

不能選相鄰的數字。

而這其實就是最緊條件

Pizza with 3n slices (leetcode 1388)

證明：選(包含頭尾)不相鄰的數字 = 合法的披薩選法

證明 → (數歸 + 構造法)

遇到黑白相間的，一定從兩側開始選。

選

不選

兩個黑白相間的中間一定有兩個不選以上。
- 這個時候你選他們兩側，最終會併起來。

這個程序可以一直進行到只剩一條黑白相間 (因為 n 有限)。
- 此時從兩側選一定選的完。 (Base Case)

選

如果選中間，之後白色會接起來，這導致之後無法同時選兩個。

證明 ← : Trivial

得證：選不相鄰的數字 ⇔ 合法的披薩選法。

Pizza with 3n slices (leetcode 1388)

現在有 3 $n$ 個數字陣列 A，請最大化你選的 n 個數字。

你選的數字不能相鄰，包含頭尾。

想到這裡其實你就已經有一個DP解了。(不考慮頭尾同時選)

DP[n][k][c] = 前 n 個數字中，選 k 個數字，有沒有選到第n個數字 (有的話 c = 1，否則 c = 0)

\begin{cases} DP_{n, k, 1} = DP_{n-1, k-1, 0} + A_{n} \\ DP_{n, k, 0} = \max ( DP_{n-1, k, 0}, DP_{n-1, k, 1} ) \end{cases}

不過要怎麼處理頭尾不同時選呢？

分開處理 \begin{cases} DP_{3n-1, n, 0} & 不選尾 \\ 把 A 反過來找 DP_{3n-1, n, 0} & 不選頭 \end{cases}

O(3n \times n)

Pizza with 3n slices (leetcode 1388)

現在有 3 $n$ 個數字陣列 A，請最大化你選的 n 個數字。

你選的數字不能相鄰，包含頭尾。

想到這裡其實你就已經有一個DP解了。

O(n^2)

但這題其實有貪心解！他可以做到

O(n \log n)

k = 2, [8, 9, 8, 6, 1, 1]

如果我們按照排序來選數字呢？

k = 1, [8, 9, 8, 6, 1, 1]

這不是不行嗎...？

看起來沒有貪心選擇的性質啊？

Pizza with 3n slices (leetcode 1388)

現在有 3 $n$ 個數字陣列 A，請最大化你選的 n 個數字。

你選的數字不能相鄰，包含頭尾。

k = 2, [8, 9, 8, 6, 1, 1]

k = 1, [8, 9, 8, 6, 1, 1]

看起來沒有貪心選擇的性質啊？

有沒有機制讓我們反悔呢...?

假設最大值是 9，那麼只會有兩種狀況

最佳解有 9，這就沒問題。
最佳解沒有 9 呢？
- 那麼最佳解一定會選 9 的周圍兩個，也就是 8 8。
- 為什麼？

Pizza with 3n slices (leetcode 1388)

現在有 3 $n$ 個數字陣列 A，請最大化你選的 n 個數字。

你選的數字不能相鄰，包含頭尾。

int n = slices.size() / 3, ans = 0;
while (n--) {
    auto m = max_element(slices.begin(), slices.end());
    auto r = (m + 1 == slices.end() ? slices.begin() : m + 1);
    auto l = (m == slices.begin() ? slices.end() : m - 1);
    ans += *m;
    *m = *l + *r - *m;
    if (l < r)
        slices.erase(r), slices.erase(l);
    else
        slices.erase(l), slices.erase(r);
}
return ans;

ans = 0
n = len(slices) // 3
for _ in range(n):
    idx = slices.index(max(slices))
    ans += slices[idx]
    slices[idx] = slices[idx-1] + \
        slices[(idx+1) % len(slices)] - slices[idx]
    if idx == len(slices)-1:
        del slices[idx-1]
        del slices[0]
    else:
        del slices[idx+1]
        del slices[idx-1]
return ans

C++

Python

這不是嗎...

O(n^2)

Pizza with 3n slices (leetcode 1388)

選 C = 扣掉 BCD 的最佳解 + C

證明： [..., A, B, C, D, E, F, ...] 中，
其中 C 為最大值，那麼最佳解只會有兩種狀況

C 在最佳解
B D 同時在最佳解

選 D 不選 B : 扣掉 BCDE 的最佳解 + D

上面比較大，
因為有更多選擇

上面比較大，
因為前提 C >= D

選 B 不選 D 同理。

所以如果你不選 C，你一定會同時選 C 的兩側

按照同樣的邏輯，如果 B + D - C > A, E 但 B D 不在最佳解，那麼 A C E 一定在最佳解。

Pizza with 3n slices (leetcode 1388)

選 BD = 扣掉 ABCDE 的最佳解 + (B + D)

證明： [...Y, A, B, C, D, E, F, X...] 中，
其中 B + D - C > A, E，那麼最佳解只會有兩種狀況

B D 同時在最佳解
A C E 同時在最佳解

選 CE 不選 A : 扣掉 ABCDEF 的最佳解 + (C + E)

上面比較大，
因為有更多選擇

上面比較大，
因為前提

選 AC 不選 E 同理。

這也就表示著你的反悔總是在反轉黑白交替的鍊。

選變不選 / 不選變選

如果兩個黑白相間的鍊碰再一起呢？自己證明看看吧！

Pizza with 3n slices (leetcode 1388)

這不是嗎...

O(n^2)

其實我們可以使用 Doubly Linked List + Priority Queue 來實作這個功能！

對每個點做 Linked List。
對每個點放入 PQ，並記錄這個數字在 Linked List 的位置
抓出最大值，合併左右。
1. 維護 Linked List，把三個點刪掉，並做一個新的點鍊起來
2. 維護 PQ，將刪掉的三個點標記起來，避免之後 pop 會出問題 (Lazy Deletion Technique)。之後再重新 push 一個新的。

Doubly Linked List

Priority Queue / heap

[(9, 1), (8, 0), (8, 2), (6, 3), (1, 4), (1, 5)]

O(n \log n)

O(n)

Pizza with 3n slices (leetcode 1388)

struct Node{
    int l, r, v;
};
int n = slices.size() / 3, ans = 0, cnt = 0;
// Build Circular Doubly Linked List
int top = 3*n;
vector<Node> LR(4*n+1);
priority_queue<pair<int, int>> PQ;
for (int i=0; i<3*n; i++) {
    LR[i] = {i ? i-1 : 3*n-1,   // l
        (i == 3*n-1) ? 0 : i+1, // r
        slices[i]};             // v
    PQ.push({slices[i], i});
}
while (cnt != n) {
    auto [_, m] = PQ.top();
    PQ.pop();
    if (LR[m].v == -1)
        continue;
    auto [l, r, v] = LR[m];
    int ll=LR[l].l, rr=LR[r].r;
    ans += v, cnt += 1;
    int new_v = LR[l].v + LR[r].v - v;
    LR[ll].r = LR[rr].l = top;
    LR[top] = {ll, rr, new_v};
    LR[l].v = LR[m].v = LR[r].v = -1;
    PQ.push({new_v, top++});
}
return ans;

n = len(slices) // 3
# Build Circular Doubly Linked List
LR = [None] * (4*n+1)
for i in range(3*n):
    LR[i] = [i-1, i+1, slices[i]]
LR[0][0] = 3*n-1
LR[3*n-1][1] = 0

# Make Heap
q = [(-x, i) for i, x in enumerate(slices)]
heapq.heapify(q)
ans = []
top = 3*n
while len(ans) != n:
    v, m = heapq.heappop(q)
    if LR[m] is None:
        continue
    l, r, v = LR[m]
    ans.append(v)
    new_v = LR[l][2] + LR[r][2] - v
    ll, rr = LR[l][0], LR[r][1]
    LR[ll][1], LR[rr][0] = top, top
    LR[top] = [ll, rr, new_v]
    LR[l] = LR[m] = LR[r] = None
    heapq.heappush(q, (-new_v, top))
    top += 1

return sum(ans)

C++

Python

你可以真的寫一個 Linked List，但我好懶

股票買賣 - IV

Best Time to Buy and Sell IV (leetcode 188)

標程是 DP O(nk)，但可以貪心 O(n) / O(nlogn)

AI-666 賺多少 (2017 學科全國賽 - P6, tioj 2039)

根據出題者說，這題標程就是貪心 O(n) / O(nlogn)，
但一票人都用 DP + Aliens 優化 O(nlogC)

Best Time to Buy and Sell IV (leetcode 188)

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

舉例來說：

(4 - 1) = 3

Prices = [1,3,2,4]

k = 1

[1,3,2,4]

(3 - 1) + (4 - 2) = 4

k = 2

[1,3,2,4]

直觀來說，你會怎麼做？

好像真的是太難了...

先從簡單的開始想

Best Time to Buy and Sell Stock (leetcode 121)

限制 k = 1

"最大子區間和" 的弱化版。

利用掃描線紀錄：

當前最小值
當前答案 = 現在價格-之前最小值

m = prices[0]
a = 0
for p in prices:
  m = min(m, p)
  a = max(a, p-m)
return a

Python

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

Best Time to Buy and Sell Stock II (leetcode 122)

k = ∞，可以當天賣了又買

ans = 0
for i in range(1, len(prices)):
  if prices[i-1] < prices[i]:
    ans += prices[i] - prices[i-1]
return ans

Python

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

如果我們可以當天賣了又買，
那麼其實我們可以考量昨天跟今天。

昨天 < 今天，那昨天買今天賣
昨天 >= 今天，我就不該昨天買

那麼如果你想要解原題該怎麼辦呢？

我們「大概」會從賺最多的開始選。

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

Best Time to Buy and Sell IV (leetcode 188)

我們「大概」會從賺最多的開始選。

等等，這是對的嗎？

選擇兩次交易 (A, B) (B, C) \\\rightarrow B-A + C-B = C-A

根本可以選一次交易就好！ \\ (A, C) \rightarrow C-A

如果事先處理掉這種 Case 呢？

那就沒有其他 Case 嗎？

Best Time to Buy and Sell IV (leetcode 188)

考慮所有相鄰的兩次交易

比起用兩次交易 \\ (v_0, p_0), (v_1, p_1) \\ 不如直接一次賺完 \\ (v_0, p_1)

如果只有一次機會選 (v_0, p_1)。\\

如果有兩次機會，分兩次賺(v_0, p_0), (v_1, p_1) \\

v_0

≈

p_0

v_1

p_1

v_0 \le p_0 \le v_1 \le p_1

v_0

≈

p_0

v_1

p_1

v_0 \le v_1 \le p_0 \le p_1

所以我們可以合併成 (v_0, p_1)。

並且有個反悔選項 (v_1, p_0)。

選了 (v_0, p_1) \rightarrow 省略中間的點。\\ 多選了 (v_1, p_0) \rightarrow 拆兩時段買。

v: valley 山谷

p: peak 山峰

Best Time to Buy and Sell IV (leetcode 188)

考慮所有相鄰的兩次交易

只有一次機會選 (v_0, p_0)。\\

有兩次機會，選(v_0, p_0), (v_1, p_1) \\

v_0

≈

p_0

v_1

p_1

v_0 \le v_1 \le p_1 \le p_0

符合原本先選大的貪心！

但 (v1, p1) 有可能之後合併，所以等後面處理。

如果之後需要合併，從 v_1 選一定比較好。

貪心會錯是因為有可能會「合併」

但 (v_0, p_0) 再也不會跟後面的合併。

所以可以把 (v_0, p_0) 剔除要合併的隊列。

v_0

≈

p_0

v_1

p_1

v_1 \le v_0

Best Time to Buy and Sell IV (leetcode 188)

考慮所有相鄰的兩次交易

v_0

≈

p_0

v_1

p_1

v_0 \le p_0 \le v_1 \le p_1

v_0

≈

p_0

v_1

p_1

v_0 \le v_1 \le p_0 \le p_1

v_0

≈

p_0

v_1

p_1

v_0 \le v_1 \le p_1 < p_0

v_0

≈

p_0

v_1

p_1

v_1 \le v_0

直接合併

合併 + 反悔

等後面合併

放棄 (v₀, p₀)

等後面合併

等合併 (v_0, p_1)

等合併 (v_0, p_1) \\ 不等合併 (v_1, p_0)

等合併 (v_0, p_0) \\ 等合併 (v_1, p_1)

等合併 (v_1, p_1) \\ 不等合併 (v_0, p_0)

Best Time to Buy and Sell IV (leetcode 188)

考慮所有相鄰的兩次交易

v_0 \le p_0 \le v_1 \le p_1

等合併 (v_0, p_1)

v_0 \le v_1 \le p_0 \le p_1

等合併 (v_0, p_1) 不等合併 (p_1, v_0)

v_0 \le v_1 \le p_1 \le p_0

兩個都繼續等

v_1 \le v_0

等合併 (v_1, p_1) 不等合併 (v_0, p_0)

實際做做看吧！

Prices = [1, 5, 2, 3, 6, 0, 2]

等待合併的

不等合併的

(1, 5)

(2, 3)

(3, 6)

(0, 2)

(2, 6)

(1, 6)

Rule 1: 合併

Rule 2: 合併 + 反悔

(2, 5)

Rule 3: 等待

(1, 6)

從 (1, 6), (2, 5), (0, 2) 按照賺最多的開始選。

stack<pair<int, int>> S;        
vector<int> options;
for (int i=1; i<prices.size(); i++) {
    if (prices[i-1] < prices[i])
        S.push({prices[i-1], prices[i]});
    while (S.size() >= 2) {
        auto [v1, p1] = S.top(); S.pop();
        auto [v0, p0] = S.top(); S.pop();
        if (p0 <= v1) {
	        // Case 1: 合併
            S.push({v0, p1});
        } else if (v0 >= v1) {
            // Case 4: 踢掉 (v0, p0)
            options.push_back(p0 - v0);
            S.push({v1, p1});
        } else if (p1 >= p0) {
            // Case 2: 合併 + 反悔
            options.push_back(p0 - v1);
            S.push({v0, p1});
        } else {
            // Case 3: 不做事，等待下次合併
            S.push({v0, p0});
            S.push({v1, p1});
            break;
        }
    }
}
while (!S.empty()) {
    auto [v, p] = S.top();
    S.pop();
    options.push_back(p - v);
}
sort(options.begin(), options.end(), greater{});
int ans = 0;
for (int i=0; i<k && i < options.size(); i++)
    ans += options[i];
return ans;

pairs = deque()
regret = []
for i in range(len(prices)-1):
	v1, p1 = prices[i], prices[i+1]
	# 如果價格變差，跳過
	if v1 >= p1:
		continue
	pairs.append([v1, p1])
	while len(pairs) >= 2:
		(v0, p0), (v1, p1) = pairs[-2], pairs[-1]
		# Case 1: 合併
		if v0 <= p0 <= v1 <= p1:
			pairs[-2][1] = p1
			pairs.pop()
		# Case 2: 合併 + 反悔
		elif v0 <= v1 <= p0 <= p1:
			pairs[-2][1] = p1
			pairs.pop()
			regret.append([v1, p0])
		# Case 3: 等待下次合併 (直接跳掉)
		elif v0 <= v1 <= p1 <= p0:
			break
		# Case 4: 踢掉 (v0, p0)
		elif v0 >= v1:
			del pairs[-2]
			regret.append([v0, p0])

# 選最大的 k 個總和
profits = sorted([b-a for a, b in regret + list(pairs)], reverse=True)
return sum(profits[:k])

C++

Python

Best Time to Buy and Sell IV (leetcode 188)

你可能會想說：

雖然前面是 O(n) 處理沒錯，

但最後一步不是要 sort 後選前 k 個加起來嗎？

sort 應該是 O(n log n)？

其實，給定一個未排序的序列找出第 k 大數字是 O(n)

這個算法叫做 Quick Select (一個非常麻煩的演算法)

使用這個方法後，用 for 迴圈把比第 k 個數字還要小的加起來就是答案了。

補充: O(n \log n) \rightarrow O(n)

Best Time to Buy and Sell IV (leetcode 188)

Quick Select 的 C++ built-in function

k = min(k, (int)options.size());
nth_element(options.begin(), options.begin()+k, options.end(), greater{});
int ans = 0;
for (int i=0; i<k; i++)
  ans += options[i];
return ans;

Python 沒有，自己寫吧🙃

補充: O(n \log n) \rightarrow O(n)

\begin{cases} DP_{n, k, 1} = \max \begin{cases} DP_{n-1, k-1, 0} - P_{n} & 以 P_n 價格買股\\ DP_{n-1, k, 1} & 跳過這天，繼續持股 \end{cases} \\ DP_{n, k, 0} = \max \begin{cases} DP_{n-1, k, 0} & 跳過這天\\ DP_{n-1, k, 1} + P_n & 以 P_n 價格賣股 \end{cases} \end{cases}

給定數列 P（第 i 天的股票價格）和整數 k，
求最多進行 k 筆買賣時的最大利潤。
此外，你只能同時持有一張股票。

Best Time to Buy and Sell IV (leetcode 188)

仔細想想其實有 DP 解，時間複雜度

DP[n][k][c] = 前 n 天買了 k 次，有(c=1)沒有(c=0)持股時的最大利潤

O(nk)

雖然DP比較好想但貪心複雜度是，快很多！

O(n)

不過這題 DP 可以優化，叫做 Aliens 優化，可以做到 O(N log P)

int dp[1000][101][2] = {}, visit[1000][101][2] = {};
int rec(vector<int>& prices, int n, int k, bool c) {
    if (n == -1 && k == 0 && c == 0) 
    	return 0;
    if (n == -1 || k == -1) 
    	return INT_MIN + 1000;
    if (visit[n][k][c]) 
    	return dp[n][k][c];
    visit[n][k][c] = true;
    if (c == 1)
        return dp[n][k][c] = max(
                rec(prices, n-1, k-1, 0)-prices[n], 
                rec(prices, n-1, k, 1));
    else
        return dp[n][k][c] = max(
                rec(prices, n-1, k, 1)+prices[n], 
                rec(prices, n-1, k, 0));
}
int maxProfit(int k, vector<int>& prices) {
    int ans = 0;
    for (int i=0; i<=k; i++)
        ans = max(ans, rec(prices, prices.size()-1, i, 0));
    return ans;
}

C++

Best Time to Buy and Sell IV (leetcode 188)

def maxProfit(self, k: int, prices: List[int]) -> int:
    dp = {}
    def rec(prices, n, k, c):
        if n == -1 and k == 0 and c == 0:
            return 0
        if n == -1 or k == -1:
            return float('-inf')
        if (n, k, c) not in dp:
            if c == 1:
                dp[n, k, c] = max(
                    rec(prices, n-1, k-1, 0) - prices[n],
                    rec(prices, n-1, k, 1)
                )
            else:
                dp[n, k, c] = max(
                    rec(prices, n-1, k, 1) + prices[n],
                    rec(prices, n-1, k, 0)
                )
        return dp[n, k, c]
    ans = 0
    for i in range(0, k+1):
        ans = max(ans, rec(prices, len(prices)-1, i, 0))
    return ans

Python

Best Time to Buy and Sell IV (leetcode 188)

貪心大結

貪心小小結

通靈解法

觀察題目

可能是
貪心題

想到一個
「可能對」
的解法

構造反例
Edge Case

是錯的！

找不到反例

開始寫！

通靈不出解法

數學分析

自己生測資看看

複習一下所有上課題目

主題	題目名稱	大概作法
掃描線貪心	線段覆蓋長度 (APCS)	掃描線紀錄當前覆蓋到哪。
	最大子區間和	先算出區間和，再想辦法對區間和掃描。
	最大周長三角形	數學推導，觀察從最大開始掃描。
	生產線 (APCS)	跟線段覆蓋長度作法差不多。
	超級洗衣機	維護掃描線前的性質 (已經被擴散完)。
	基地台 (APCS)	簡化問題後，用掃描線判斷 r 是否夠大 + 對 r 二分搜尋。
順序類貪心	誰先晚餐	盲猜吃最久的先做。或者利用交換判別誰該放前面。
	物品堆疊 (APCS)	基本上只能數學推導，很難通靈。
	Add All	通靈每次都使用最小的兩個數字，需要用 Priority Queue。
反悔貪心	加油站問題	將之後有可能會反悔的選項，利用反悔堆 (PQ) 紀錄起來
反悔貪心	IPO	加油站的對偶問題，做個問題轉換後題目就等於加油站。
順序+選擇類貪心	不相交區間	利用數學推導推出順序，再思考需不需要反悔貪心。
順序+選擇類貪心	湖畔大樓	利用數學推導推出順序，再思考如何反悔貪心。
匹配類貪心	餅乾分配	觀察條件最嚴苛的變數 (最難被滿足的小孩)，以此推規律
匹配類貪心	生產線 (APCS)	數學推導判斷怎麼匹配，或者依照算幾不等式的直覺。
反悔貪心 II	分 Pizza 問題	將題目轉變後，思考如果選擇一個選項，想反悔要怎麼辦。
反悔貪心 II	買賣股票問題	同 Pizza 問題，想想甚麼條件下可以做出反悔選項。

貪心問題種類

選擇類貪心：
- 這類題目通常是 DP。數字太大就表示有個規則，通常不難。
掃描線貪心：
- 這類題目很難猜，基本上通常都是要算出每個位置的什麼東西。
  - 生產線就是算出每個位置的 w
  - 超級洗衣機維護每個位置都是水平面。
  - 最大子區間和算出每個位置當區間的右界的答案。
順序類貪心：
- 這類題目基本上就是問你怎樣的順序會是最好的。
  - 這類題目很難 DP，所以通常都是考貪心或者固定的演算法。
反悔貪心：
- 基本上會有一個條件，你要滿足這個條件才可以繼續下去。
匹配類貪心：
- 通常你看的出來題目長怎樣，你看不出來的不會在 APCS 出現。

選擇類貪心 - 練習題

題目名稱	來源	備註
Product of Digits	Zerojudge d418

掃描線貪心 - 練習題

題目名稱	來源	備註
支點切割	APCS 2018 / 2 - 3, zj h028	用區間和做轉移
找最接近 k 的矩形和	Leetcode 363	做二維的區間和是 O(n^4)
投資遊戲	zj m373	APCS 2023/10 - 4 (40%) 100% 用貪心也可以但難
Jump Game	Leetcode 55
Jump Game II	Leetcode 45
Set Intersection Size at least two	Leetcode 757
砍樹	APCS 2020 / 1 - 3, zj h028	類洗衣機
Split Array Largest Sum	Leetcode 410	+二分搜
雙子大廈 TwinTower	TIOJ 1320	IOI Warmup 3

順序類貪心 - 練習題

題目名稱	來源	備註
Largest Number	Leetcode 179	經典題
髮廊服務優化問題	zj l243	2021 全國學科 pA
筆電販賣機	NPSC 題目

反悔貪心 - 練習題

題目名稱	來源	備註
Least Cost Bracket Sequence	TIOJ 1708	Codeforce 3D

順序+選擇類貪心 - 練習題

題目名稱	來源	備註
機器出租	Zerojudge j608	APCS 2023 / 1 - 4，選K個不相交區間
Course Schedule III	Leetcode 630	經典題，任務要求是時長+終點
烏龜塔問題	zj f347

匹配類貪心 / 其他貪心 - 練習題

題目名稱	來源	備註
The Bus Driver Problem	Zerojudge e538	非常經典的題目！
Two city scheduling	Leetcode 1029
Advantage Shuffle	Leetcode 870

題目名稱	來源	備註
Largest Merge Of Two Strings	Leetcode 1754	常見的類型

一種貪心，各種表述

Largest Rectangle in Histogram (leetcode 84)

給你一個直方圖，求其中的最大矩形面積。

舉例來說：

直觀來說，不考慮實作，你會怎麼做？

給你一個直方圖，求其中的最大矩形面積。

直觀來說，不考慮實作，你會怎麼做？

暴力搜尋它？

有沒有一個比較好的順序去爆搜掃描？

從最小高度開始。
從最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

直方圖最大矩形 - 解 1

利用線段樹 (Segment Tree) 找區間最小值

給你一個直方圖，求其中的最大矩形面積。

直觀來說，不考慮實作，你會怎麼做？

暴力搜尋它？

從最小高度開始。
從最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

有沒有一個比較好的順序去爆搜掃描？

給你一個直方圖，求其中的最大矩形面積。

從最小高度開始

觀察: 如果我們看到最小的數字，那麼以他為準的答案就是 n * 這個數字

[2, 1, 5, 6, 2, 3]

那之後呢？之後的高度都不該穿過 1，

所以應該把它切開

[2] / [5, 6, 2, 3]

[5, 6] / [3]

/ [6]

Largest Rectangle in Histogram (leetcode 84)

給你一個直方圖，求其中的最大矩形面積。

從最小高度開始

理論通過，開始實作。

[2, 1, 5, 6, 2, 3]

[2] / [5, 6, 2, 3]

將陣列每次都拆開...

如果你每找到最小值就拆開，那麼時間複雜度...
- O(n^2) 爛掉了 :(。
其實我們不用拆，用左右界就可以表達！
- 例如 [0, 6) 被 1 拆解後就會變成 [0, 1), [2, 6)。

Largest Rectangle in Histogram (leetcode 84)

給你一個直方圖，求其中的最大矩形面積。

從最小高度開始

[2, 1, 5, 6, 2, 3]

[2] / [5, 6, 2, 3]

將陣列每次都拆開 (僅用左右界表示子陣列)...

我們必須找到一個區間的最小值在哪裡。
- 直接找每個區間的最小值？
  - O(n^2) 又爛掉了 :(
- 有沒有魔法可以讓我知道區間最小值呢？
  - 有，常見的方法之一，叫做線段樹。

Largest Rectangle in Histogram (leetcode 84)

Segment Tree 線段樹

最原始的線段樹是為了解決 RMQ 問題

(Range Minimum Query)。

大方向就是把樹的點當成區間維護。

給你一個直方圖，求其中的最大矩形面積。

從最小高度開始

[2, 1, 5, 6, 2, 3]

[2] / [5, 6, 2, 3]

將陣列每次都拆開 (僅用左右界表示子陣列)...

我們必須找到一個區間的最小值在哪裡。
- 使用線段樹找到區間最小值在哪裡。
- 分治它！
- 複雜度

T(n) = 2T(\frac n2) + c \cdot \log n\\ \rightarrow O(n)

Largest Rectangle in Histogram (leetcode 84)

struct SegTree {
    // min number, it's index
    pair<int, int> min_info;
    SegTree *L, *R;
    SegTree(SegTree *L, SegTree *R, pair<int, int> min_info={INT_MAX, -1}):
        L(L), R(R), min_info(min_info){} 
    void pull() {
        min_info = min(L->min_info, R->min_info);
    }
};

SegTree* build(int L, int R, vector<int>& A) {
    // [l, r]
    if (L == R)
        return new SegTree(NULL, NULL, {A[L], L});
    int M = (L + R) / 2;
    SegTree *now = new SegTree(build(L, M, A), build(M+1, R, A));
    now->pull();
    return now;
}

pair<int, int> query(SegTree* root, int L, int R, int x, int y) {
    if (R < x || y < L) return {INT_MAX, -1};
    if (x <= L && R <= y) return root->min_info;
    int M = (L + R) / 2;
    return min(query(root->L, L, M, x, y), query(root->R, M+1, R, x, y));
}

Largest Rectangle in Histogram (leetcode 84)

C++ 線段樹 Code

Largest Rectangle in Histogram (leetcode 84)

class Solution {
public:
    int dc(SegTree *root, int x, int y, int N) {
        auto [min_v, min_idx] = query(root, 0, N-1, x, y);
        if (min_idx == -1)
            return INT_MIN;
        return max({
            (y - x + 1) * min_v,
            dc(root, x, min_idx-1, N),
            dc(root, min_idx+1, y, N)
        });
    }
    int largestRectangleArea(vector<int>& heights) {
        // Special Case:
        bool flag = true;
        for (auto h: heights)
            if (h != heights[0]) {
                flag = false;
                break;
            }
        if (flag)
            return heights[0] * heights.size();
        SegTree *root = build(0, heights.size()-1, heights);
        return dc(root, 0, heights.size()-1, heights.size());
    }
};

C++ Main Code

直方圖最大矩形 - 解 2

利用 Set 維護區間

給你一個直方圖，求其中的最大矩形面積。

直觀來說，不考慮實作，你會怎麼做？

暴力搜尋它？

從最小高度開始。
從最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

有沒有一個比較好的順序去爆搜掃描？

給你一個直方圖，求其中的最大矩形面積。

從最小高度開始

[2, 1, 5, 6, 2, 3]

[2] / [5, 6, 2, 3]

將陣列每次都拆開 (僅用左右界表示子陣列)...

我們必須找到一個區間的最小值在哪裡。
- 使用線段樹找到區間最小值在哪裡，然後分治它！
或是 ... 我們每次都找下一個最小值的區間在哪裡。
- 把所有區間都存起來查詢！

Largest Rectangle in Histogram (leetcode 84)

給你一個直方圖，求其中的最大矩形面積。

[2, 1, 5, 6, 2, 3]

[2] / [5, 6, 2, 3]

或是 ... 我們每次都找下一個最小值的區間在哪裡。

把所有區間都存起來查詢！

數字的排名: (1, 0, 4, 5, 2, 3)

[0, 6)

[0, 1), [2, 6)

/ / [5, 6, 2, 3]

[0, 0), [1, 1), [2, 6)

/ / [5, 6] / [3]

[0, 0), [1, 1), [2, 4), [5, 6)

Largest Rectangle in Histogram (leetcode 84)

給你一個直方圖，求其中的最大矩形面積。

或是 ... 我們每次都找下一個最小值的區間在哪裡。

把所有區間都存起來查詢！
- 什麼資料結構可以動態插入/找到想要的區間呢？
  - 用 set 存後用 lower_bound 查詢！

/ / [5, 6, 2, 3]

[0, 0), [1, 1), [2, 6)

/ / [5, 6] / [3]

[0, 0), [1, 1), [2, 4), [5, 6)

[2] / [5, 6, 2, 3]

[0, 1), [2, 6)

Largest Rectangle in Histogram (leetcode 84)

vector<pair<int, int>> order;
for (int i = 0; i < heights.size(); i++) {
	order.push_back({heights[i], i});
}
sort(order.begin(), order.end());
int ans = 0;
set<pair<int, int>> intervals{{0, heights.size()}};
for (auto &[height, idx] : order) {
  auto it = --intervals.lower_bound({idx, INT_MAX});
  ans = max(ans, height * (it->second - it->first));
  intervals.insert({it->first, idx});
  intervals.insert({idx+1, it->second});
  intervals.erase(it);
}
return ans;

Python 沒有內建平衡樹可以用...
所以 Python 不太能這樣寫。

Largest Rectangle in Histogram (leetcode 84)

直方圖最大矩形 - 解 3

利用 Linked List 維護區間

給你一個直方圖，求其中的最大矩形面積。

直觀來說，不考慮實作，你會怎麼做？

暴力搜尋它？

從最小高度開始。
從最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

有沒有一個比較好的順序去爆搜掃描？

給你一個直方圖，求其中的最大矩形面積。

最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

[2, 1, 5, 6, 2, 3]

觀察: 如果我們看到最大的數字，那麼他為準的答案就是這個數字

接下來我們會想辦法讓他跟其他點合併。

[2, 1, (5, 5), 2, 3]

[2, 1, (2, 2, 2, 2)]

由大到小看數字，
合併兩側比自己更大的數字。

並且每次更新答案就可以了。

我們用 Doubly Linked List 來合併！

給你一個直方圖，求其中的最大矩形面積。

最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

[2, 1, 5, 6, 2, 3]

[2, 1, (5, 5), 2, 3]

[2, 1, (2, 2, 2, 2)]

5 x 2

由大到小看數字，合併兩側比自己更大的數字。

並且每次更新答案就可以了。

6 x 1

5 x 2

答案

3 x 1

2 x 4

2 x 2

2 x 4

struct node {
  node *prev, *next;
  int h, w;
  node(int h, int w): 
    h(h), w(w), prev(NULL), next(NULL) {}
  int merge(set<node *> &deleted) {
    // left
    while (prev && h <= prev->h) {
      w += prev->w;
      node *tmp = prev;
      if (prev->prev)
        prev->prev->next = this;
      prev = prev->prev;
      deleted.insert(tmp);
      delete tmp;
    }
    // right
    while (next && h <= next->h) {
      w += next->w;
      node *tmp = next;
      if (next->next)
        next->next->prev = this;
      next = next->next;
      deleted.insert(tmp);
      delete tmp;
    }
    return w * h;
  }
};

vector<pair<int, node *>> order;
for (int i = 0; i < heights.size(); i++) {
  node *cur = new node(heights[i], 1);
  if (i) {
    order.back().second->next = cur;
    cur->prev = order.back().second;
  }
  order.push_back({heights[i], cur});
}
sort(order.begin(), order.end());
reverse(order.begin(), order.end());
int ans = 0;
set<node *> deleted;
for (auto &[h, cur] : order) {
  if (deleted.find(cur) == deleted.end()) {
    ans = max(ans, cur->merge(deleted));
  }
}
return ans;

Largest Rectangle in Histogram (leetcode 84)

如果不判斷刪除，那麼

遇到重複的數字會很麻煩

TODO

Largest Rectangle in Histogram (leetcode 84)

Python 還沒寫

直方圖最大矩形 - 解 4

利用 Disjoint Set 維護區間

給你一個直方圖，求其中的最大矩形面積。

直觀來說，不考慮實作，你會怎麼做？

暴力搜尋它？

從最小高度開始。
從最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

有沒有一個比較好的順序去爆搜掃描？

給你一個直方圖，求其中的最大矩形面積。

最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

[2, 1, 5, 6, 2, 3]

觀察: 如果我們看到最大的數字，那麼他為準的答案就是這個數字

接下來我們會想辦法讓他跟其他點合併。

[2, 1, (5, 5), 2, 3]

[2, 1, (2, 2, 2, 2)]

我們用 Disjoint Set 來合併！

由大到小看數字，
合併兩側比自己更大的數字。

並且每次更新答案就可以了。

給你一個直方圖，求其中的最大矩形面積。

最大高度開始。

Largest Rectangle in Histogram (leetcode 84)

由大到小看數字，合併兩側比自己更大的數字。

並且每次更新答案就可以了。

答案

[(1, 1, 1, 1, 1, 1)]

1 x 6

[2, 1, (2, 2, 2, 2)]

2 x 1

[2, 1, (2, 2, 2, 2)]

2 x 4

[2, 1, (5, 5), 2, 3]

3 x 1

[2, 1, (5, 5), 2, 3]

5 x 2

[2, 1, 5, 6, 2, 3]

6 x 1

TODO

boss = [i for i in range(len(nums))]
size = [1 for _ in nums]
ans = 0
def find_boss(i):
	if boss[i] != i:
		boss[i] = find_boss(boss[i])
	return boss[i]
def merge(i, j):
	i, j = find_boss(i), find_boss(j)
	if i != j:
	  if nums[i] > nums[j]:
		i, j = j, i
	boss[j] = i
	size[i] += size[j]

ary = sorted([(num, i) for i, num in enumerate(nums)]

for num, i in reversed(ary):
	if i > 0 and nums[i-1] >= nums[i]:
		merge(i-1, i)
	if i+1 < len(nums) and nums[i+1] >= nums[i]:
		merge(i, i+1)
	I = find_boss(i)
	ans = max(ans, nums[I] * size[I])
return ans

Largest Rectangle in Histogram (leetcode 84)

直方圖最大矩形 - 解 5

分治解 - Divide & Conquer

給你一個直方圖，求其中的最大矩形面積。

Largest Rectangle in Histogram (leetcode 84)

像逆序數對一樣，拆兩半後分成三種 Case

最大矩形在左半邊
最大矩形在右半邊
最大矩形卡在正中間

類雙指針(?) 通常簡單 DC 題

就是會用雙指針處理

直方圖最大矩形 - 解 6

利用 Deque 維護可能的答案

單調對列 (Monotonic Queue)

給你一個直方圖，求其中的最大矩形面積。

直觀來說，不考慮實作，你會怎麼做？

暴力搜尋它？

有沒有一個比較好的順序去爆搜？

從最小高度開始。
從最大高度開始。

3. 單調隊列

Largest Rectangle in Histogram (leetcode 84)

給你一個直方圖，求其中的最大矩形面積。

單調隊列

Largest Rectangle in Histogram (leetcode 84)

我們由左往右看數字：

2 1 5 6 2 3

你會發現 2 遇到 1 的時候，

2 的作用就完全消失了

2 1 ?

維護一個遞增數列就好。

給你一個直方圖，求其中的最大矩形面積。

單調隊列

Largest Rectangle in Histogram (leetcode 84)

2 1 5 6 2 3

維護一個遞增數列就好。

怎麼更新答案呢？

考量第二個 2

我們會結算 5 跟 6，
因為之後 5 跟 6 就再也沒用了。

結算方法：(數字大小) x (離 2 的距離)

// Terminate all
heights.push_back(0);
deque<pair<int, int>> Q;
int ans = 0;
for (int i = 0; i < heights.size(); i++) {
  // Pop
  pair<int, int> cur{heights[i], i};
  while (!Q.empty() && Q.back() > cur) {
    ans = max(ans, Q.back().first * (i - Q.back().second));
    cur.second = Q.back().second;
    Q.pop_back();
  }
  Q.push_back(cur);
}
return ans;

nums.append(0)
q = deque()
ans = 0
for i, height in enumerate(nums):
  cur = [height, i]
  while q and q[-1] > cur:
    ans = max(ans, q[-1][0] * (i-q[-1][1]))
    cur[1] = q[-1][1]
    q.pop()
  q.append(cur)
return ans

Largest Rectangle in Histogram (leetcode 84)

為了方便，會在最後放 0。

這是為了結算所有的答案。

淺入淺出 貪心算法

Intro to Greedy Algorithm Arvin Liu

前言

簡言之，貪心=通靈

前言

我是麻瓜，不會通靈

選擇類貪心

選擇類貪心

Coin Change (leetcode 322)

Coin Change (leetcode 322)

回憶一下遞迴樹

回憶一下遞迴樹

回憶一下遞迴樹

使用時機

最佳子結構

重複子問題

使用時機

最佳子結構

貪婪選擇性質

使用時機

掃描線貪心

掃描線演算法 sweep-line

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

線段覆蓋長度 APCS 2016/03 - 3 (zj b966)

基本上掃描線貪心就是...

固定一個順序後，

枚舉這個順序的點去找解。

最大子區間和

最大子區間和 (leetcode 53)

最大子區間和 (leetcode 53)

前綴和 / 區間和

前綴和 / 區間和

最大子區間和 (leetcode 53)

最大子區間和 (leetcode 53)

區間和很常考！

你知道線段樹嗎？

最大周長三角形

Largest Perimeter Triangle (leetcode 976)

最大周長三角形 (leetcode 976)

最大周長三角形 (leetcode 976)

最大周長三角形 (leetcode 976)

掃描線 + 對半拆解

Maximum Sum of 3 Non-Overlapping Subarrays (leetcode 689)

生產線 - Part 1

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

生產線 (APCS 2021/11 - 3, zj g597)

超級洗衣機

Super washing machines (leetcode 517)

Super washing machines (leetcode 517)

Super washing machines (leetcode 517)

Super washing machines (leetcode 517)

Super washing machines (leetcode 517)

Super washing machines (leetcode 517)

貪心+二分搜

基地台 (zj c575, APCS 2017/03-4)

基地台 (zj c575)

基地台 (zj c575)

基地台 (zj c575)

基地台 (zj c575)

多描述一下單調性值就可以二分搜尋

(掃描線)貪心小小結

掃描線小結

掃描線小結

貪心小小結

貪心小小結

順序類貪心

順序類貪心

選擇類貪心

順序類貪心

誰先晚餐 - 通靈

A. 誰先晚餐 (TIOJ 1072, NPSC 2005 高中決賽 PA)

A. 誰先晚餐 (TIOJ 1072)

淺入淺出貪心算法

Intro to Greedy Algorithm

Arvin Liu