MLDS HW1 Presentation
先來點療癒的東西

Outline
-
Optimization -- Visualize Optimization via PCA
-
Optimization -- Visualize Error Surface
-
Generalization -- Flatness
-
Generalization -- Sensitivity
About Outline
這不是手把手,
這是觀察。
About HW1
What is the reason?
Visualize Optimization via PCA
Target Function
Result
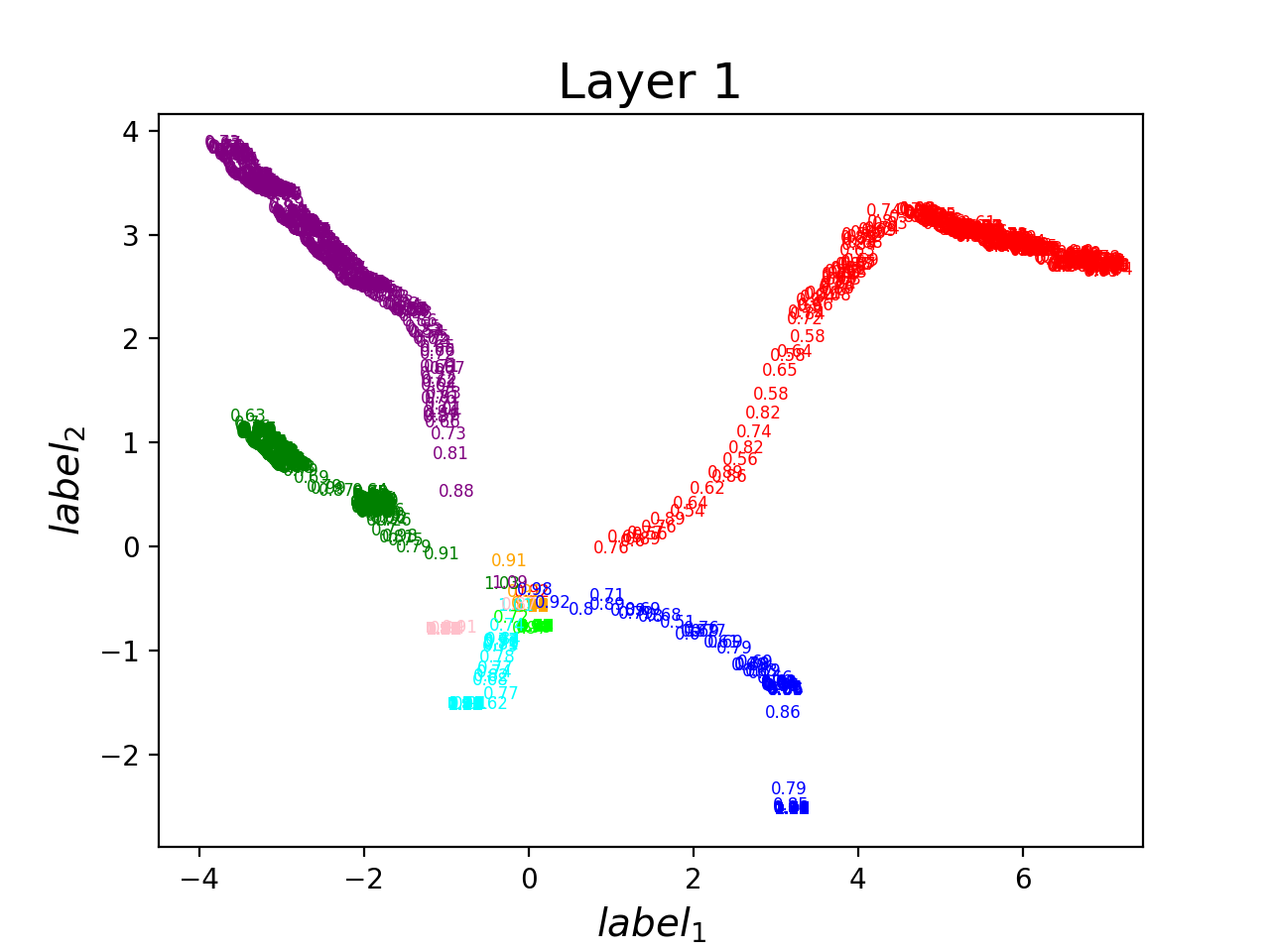
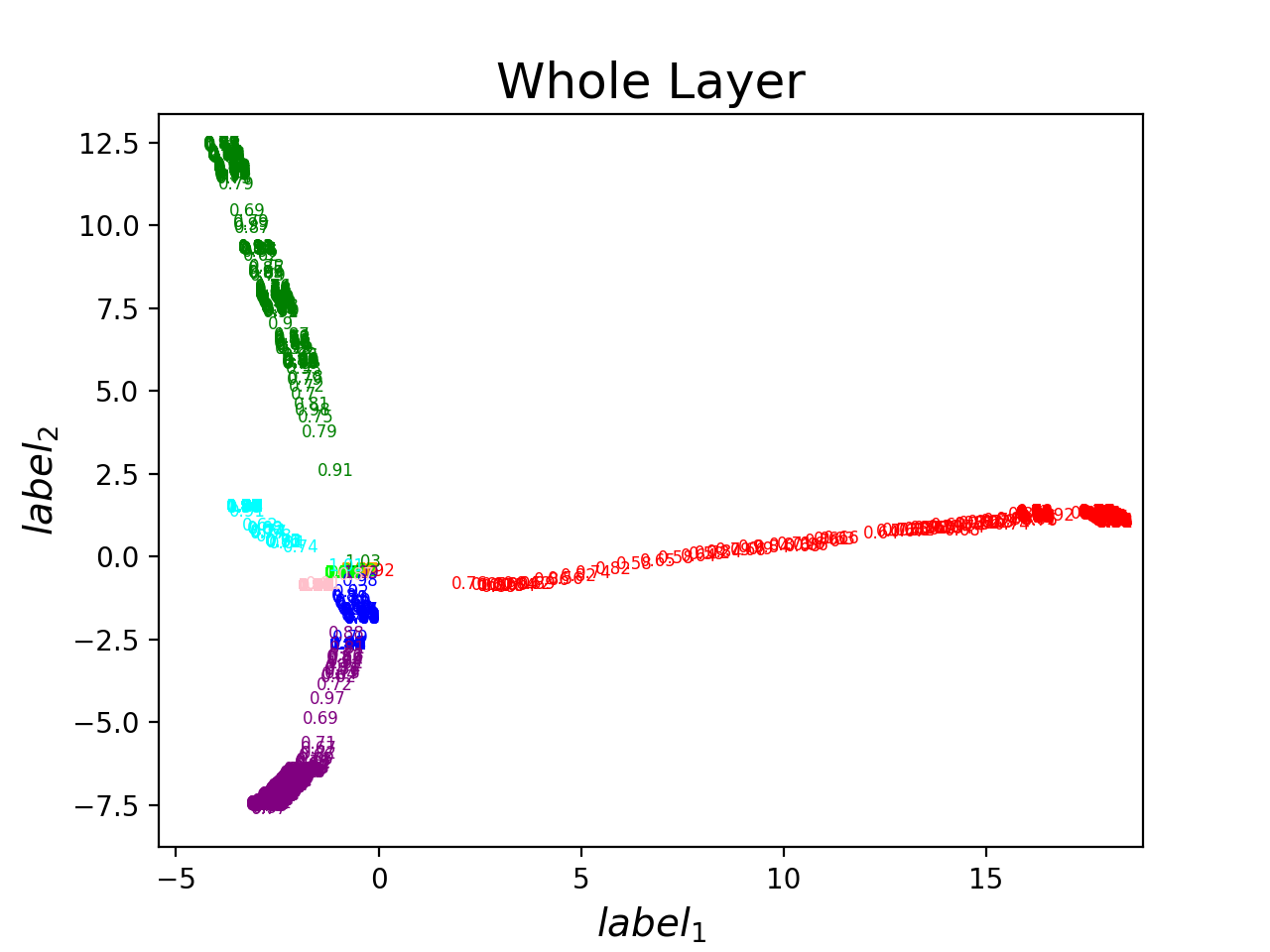
發散猜想 -> network找到不一樣的solution
Another Trial
X
Y
b2
b1,1
b1,2
b1,3
b1,10
w1,1
w1,2
w1,3
w1,10
w2,10
w2,3
w2,2
w2,1
h
做出來的結果究竟是掉到等價答案
還是不同的local minima?
. . .
| w1,1 <-> w1,2 |
| b1,1 <-> b1,2 |
| w2,1 <-> w2,2 |
Findings
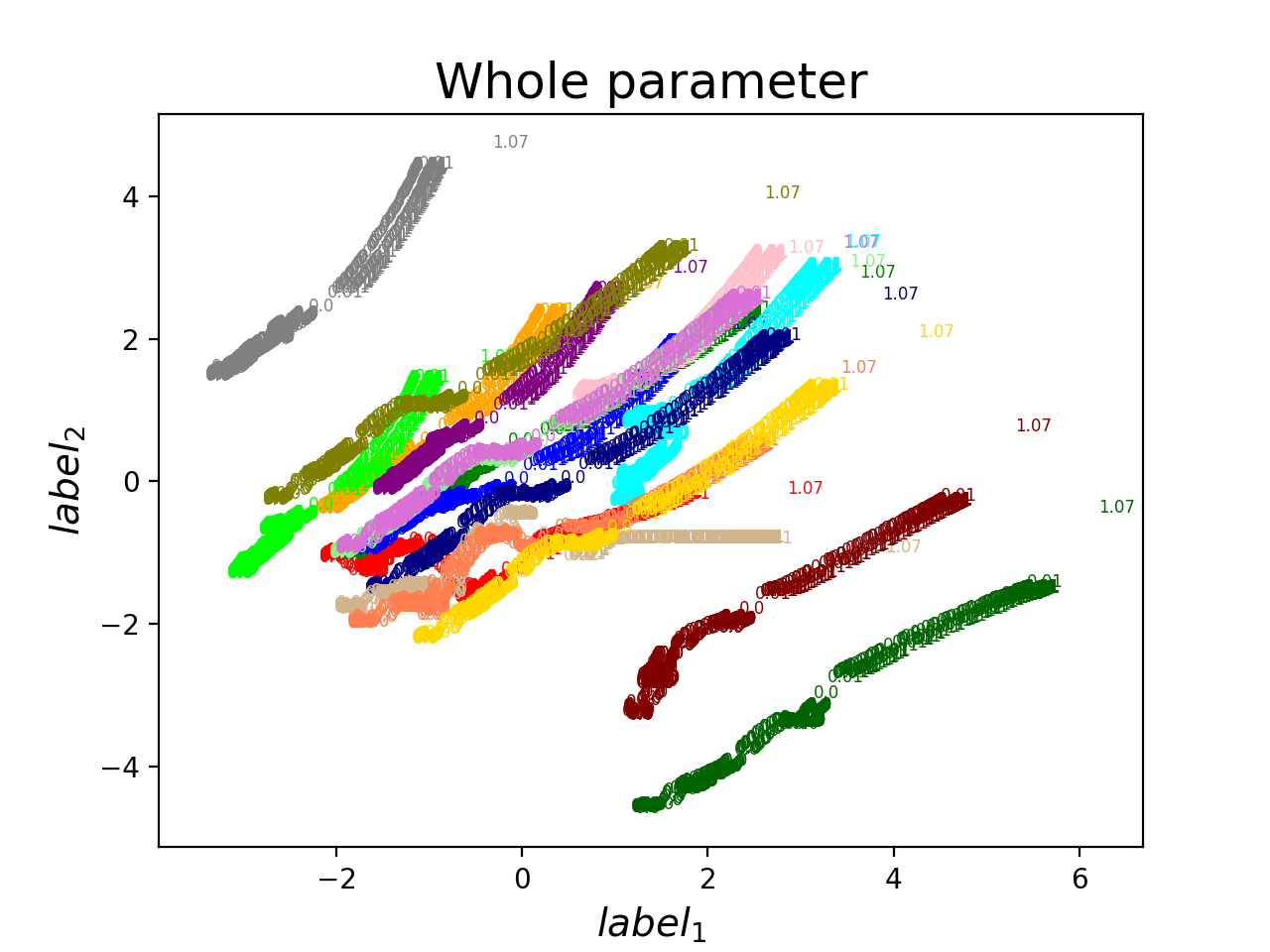
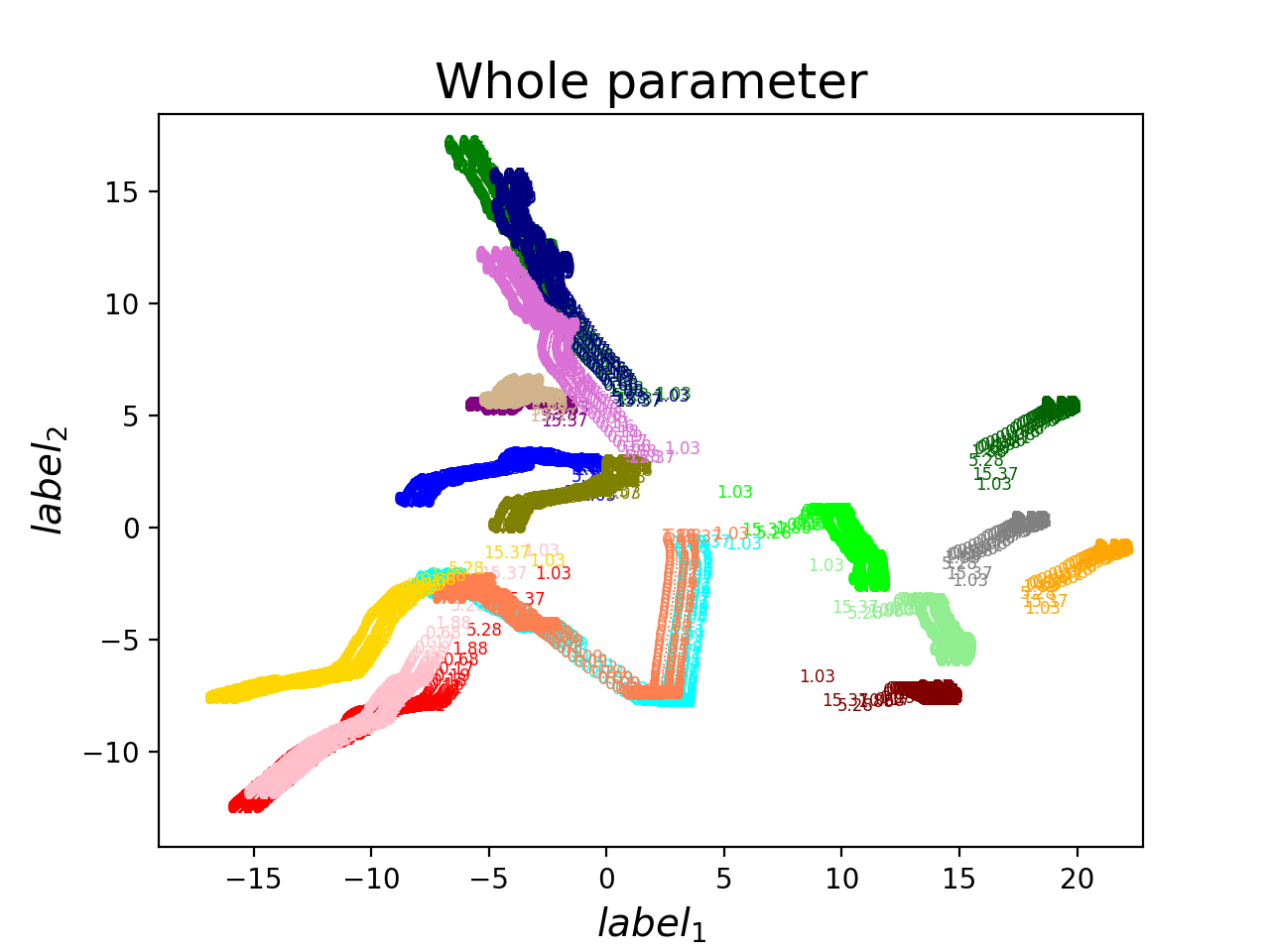
Train on [0, 1]
Train on [0, 10]
Result


Train on [0, 1]
Train on [0, 10]
The same !!!
TSNE ?
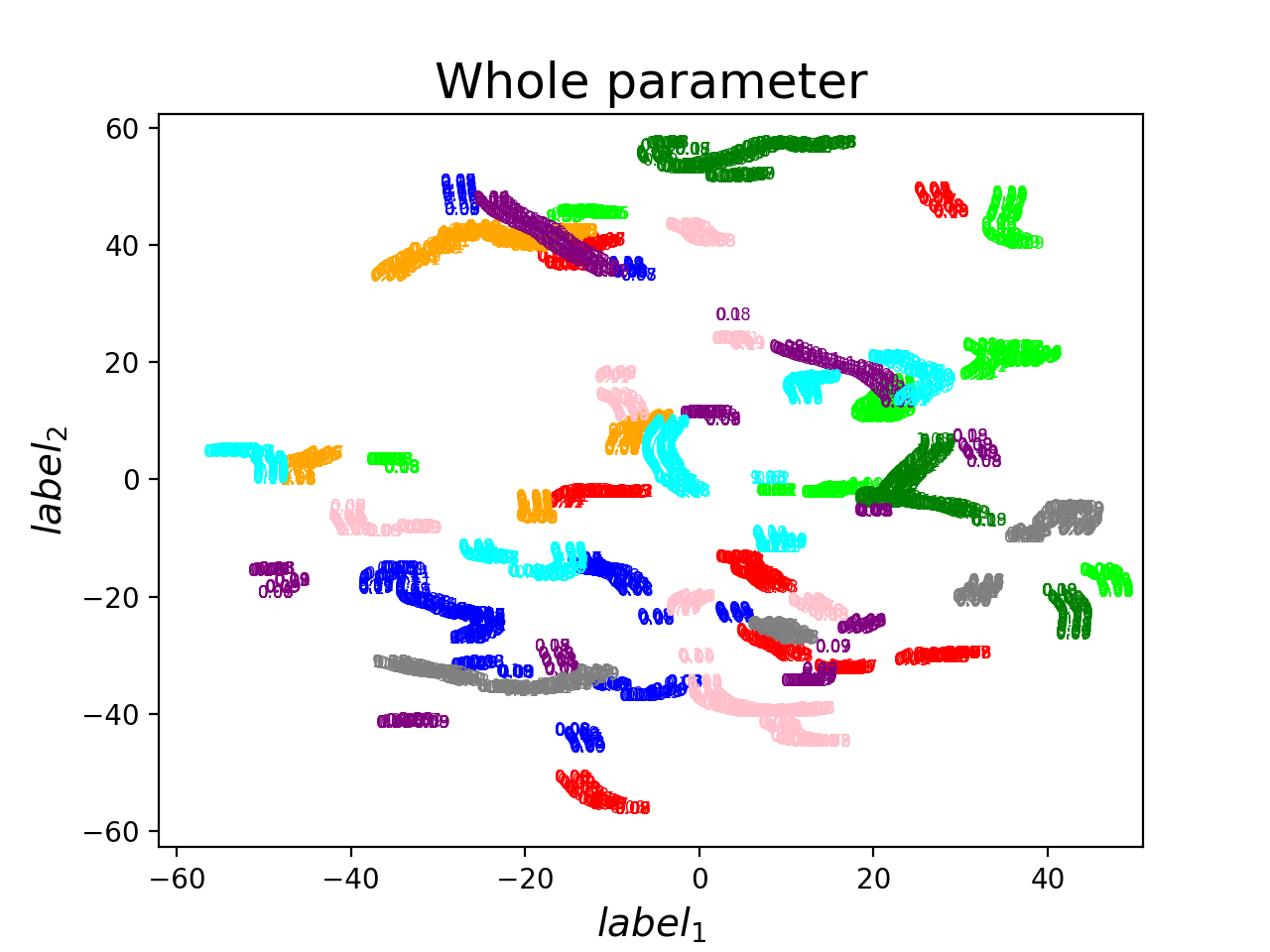
維度降太快爛掉了orz
PCA + TSNE -1
Train 4 times + Exchange 4
Only Exchange parameters

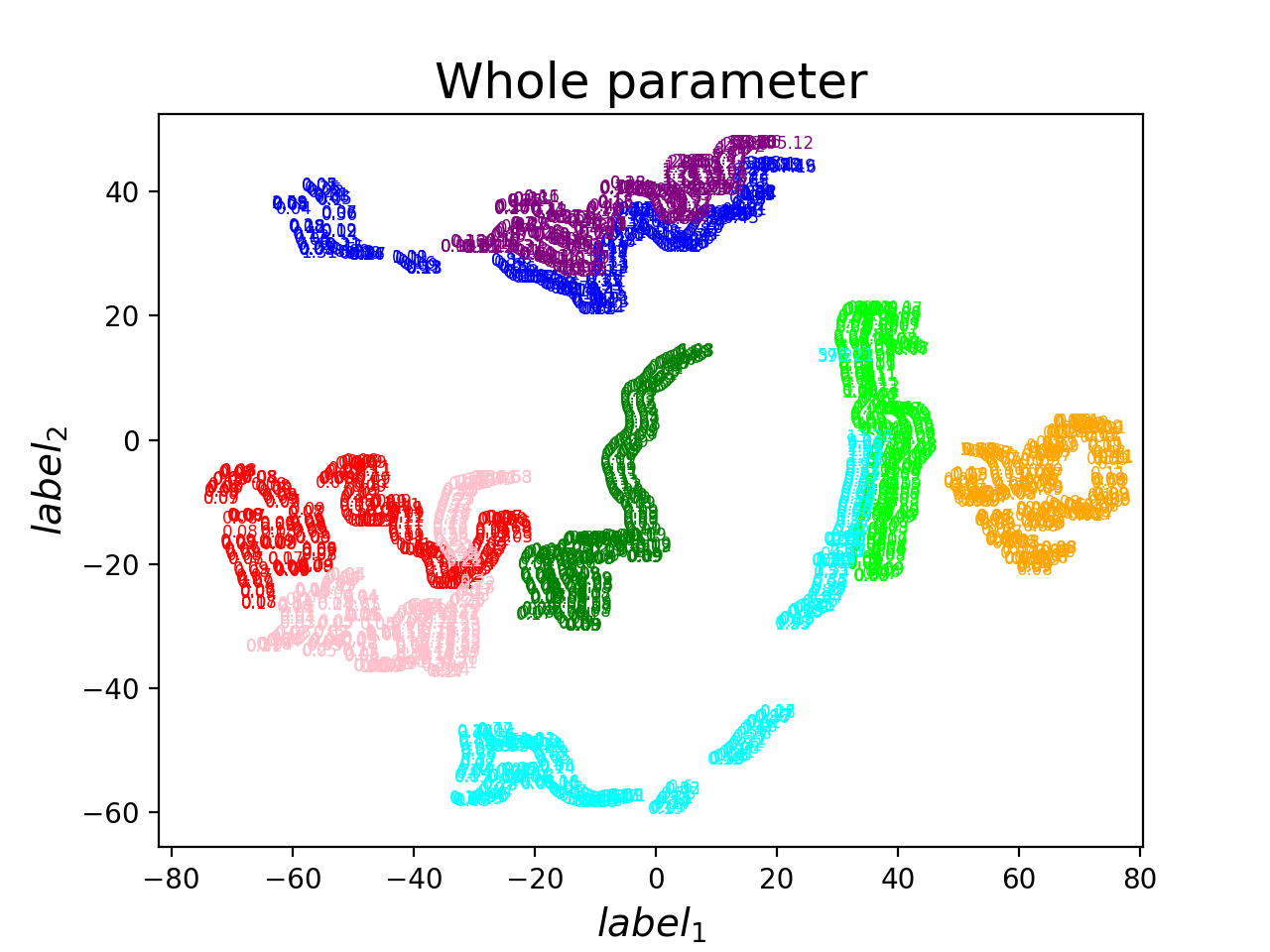
PCA + TSNE -2
Train 8 - 9次的結果 (no parameters exchange)
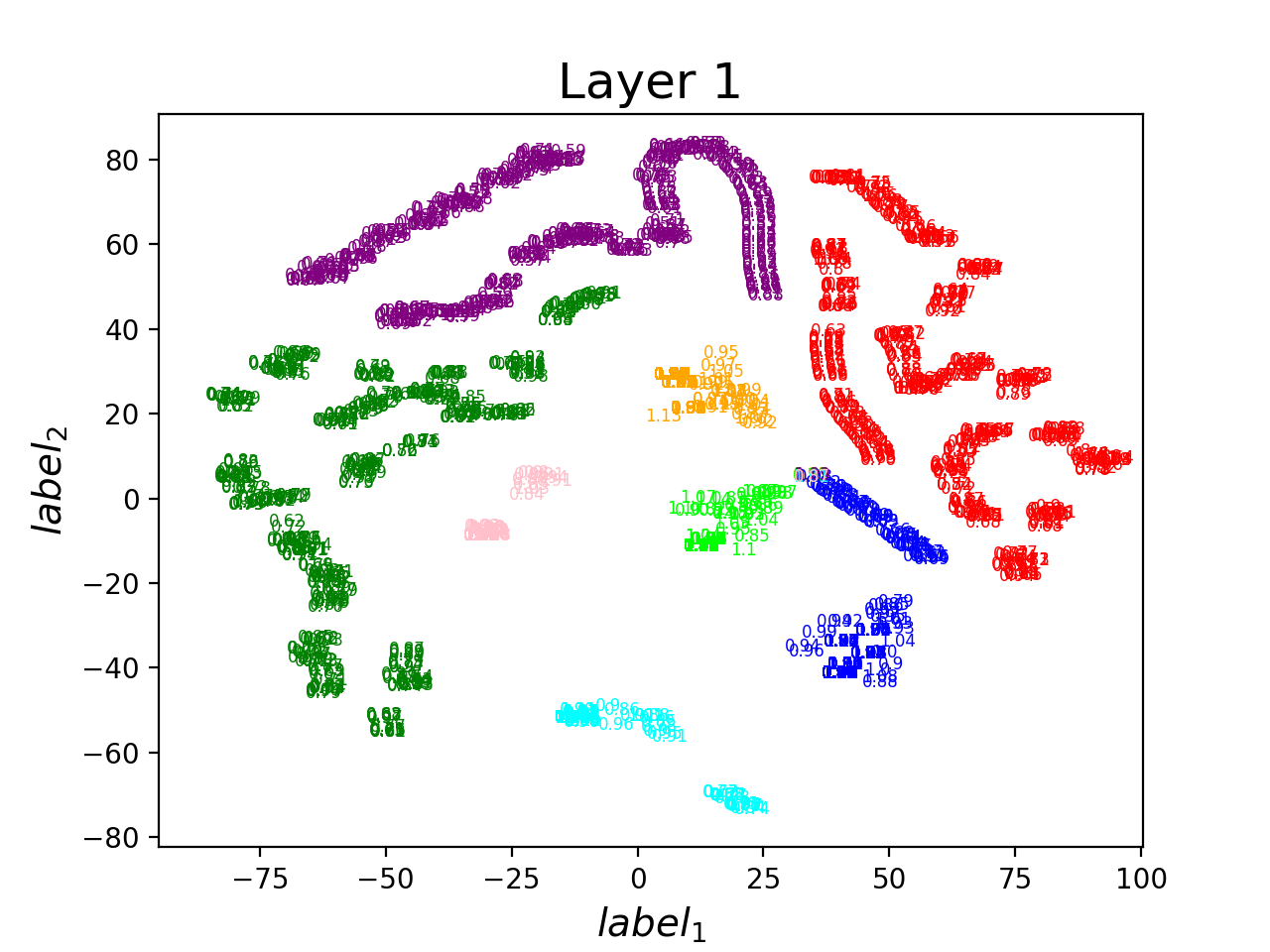
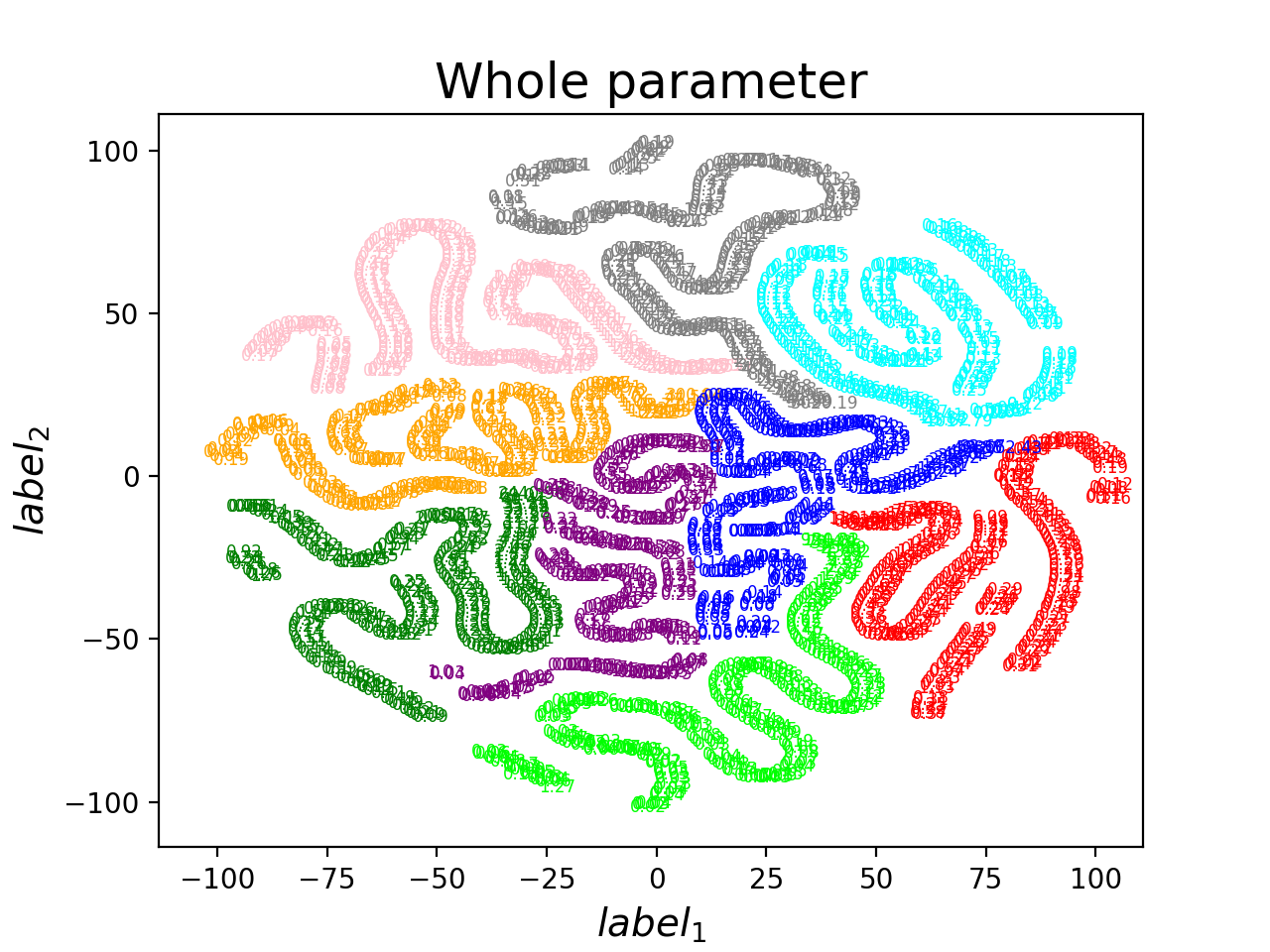
Conclusion
- initialize的位置跟training range不同應該會影響這個task的結果
- 用PCA visualize的話,直接換weight就可以看到類似的結果了
- TSNE降維一次降太多會爛掉
- PCA + TSNE好像可以確定哪些是相同的local minima,哪些不是
Visualize
Error Surface
Target Function
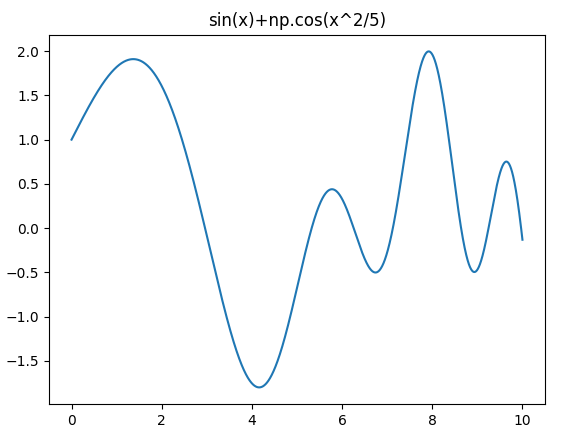
PCA(->10) & TSNE(->2)
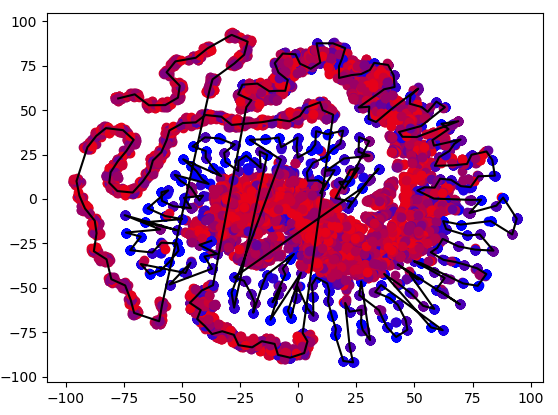
Dense with bias(1->4->4->1)(|params|=33)
New Target Function
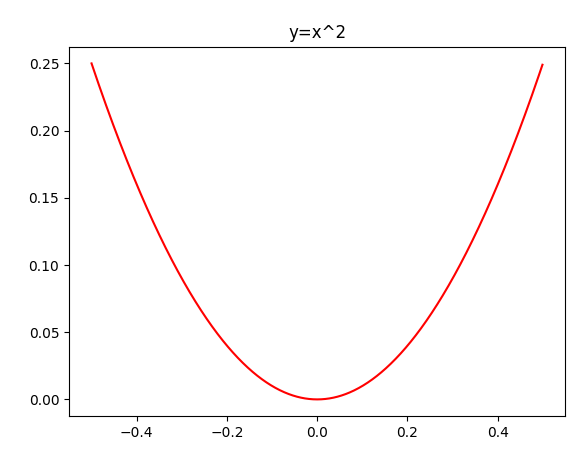
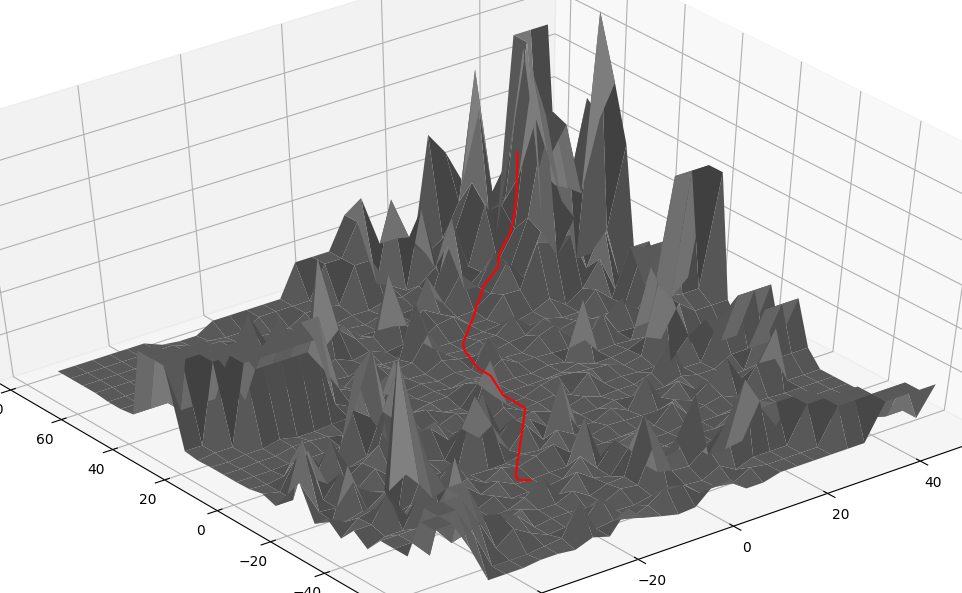
3D error surface (DNN 1,6,1 & act=cos)
Indicator of Generalization-
Flatness
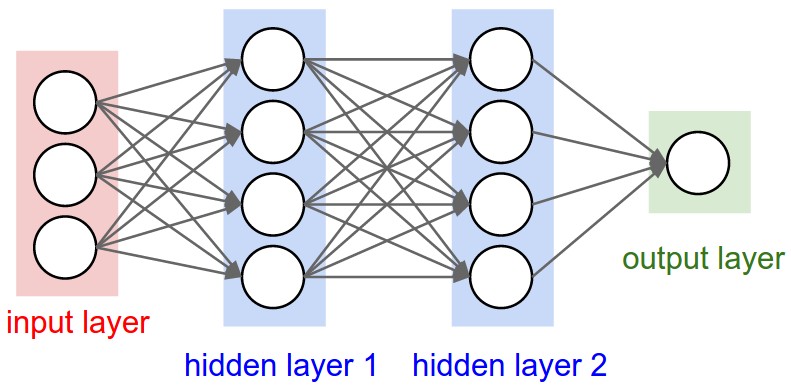
In some deep model... [28*28,5,5,5,5,5,5,5,10]
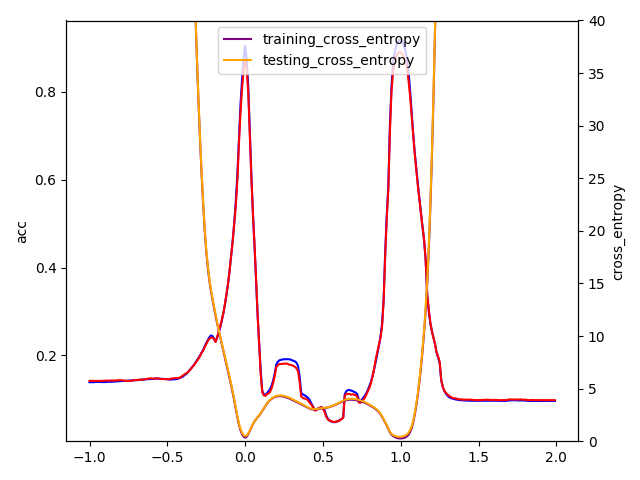
In some shallow model... [28*28,100,10]
Why There's Flattness?
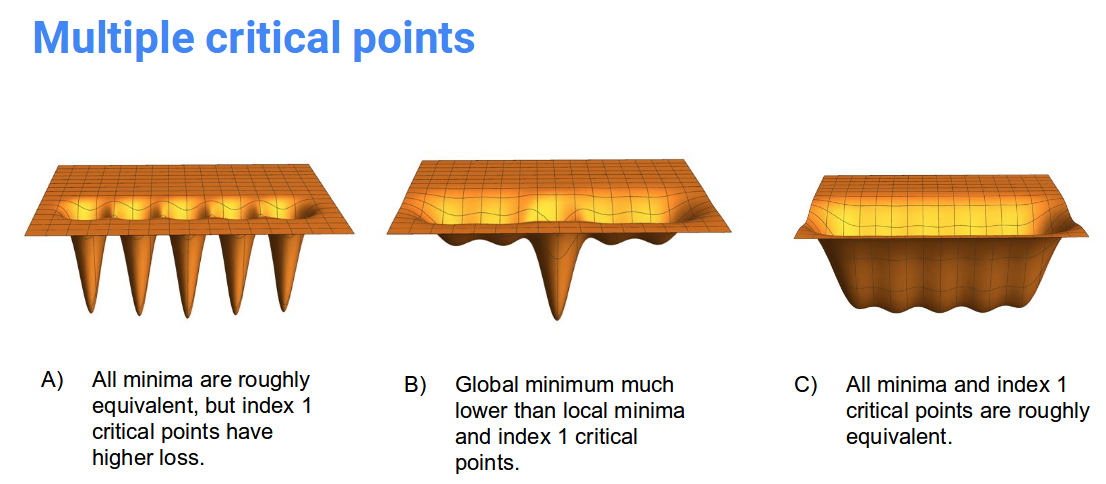
https://stats385.github.io/assets/lectures/Understanding_and_improving_deep_learing_with_random_matrix_theory.pdf
Interpolate Error Suface - t-SNE
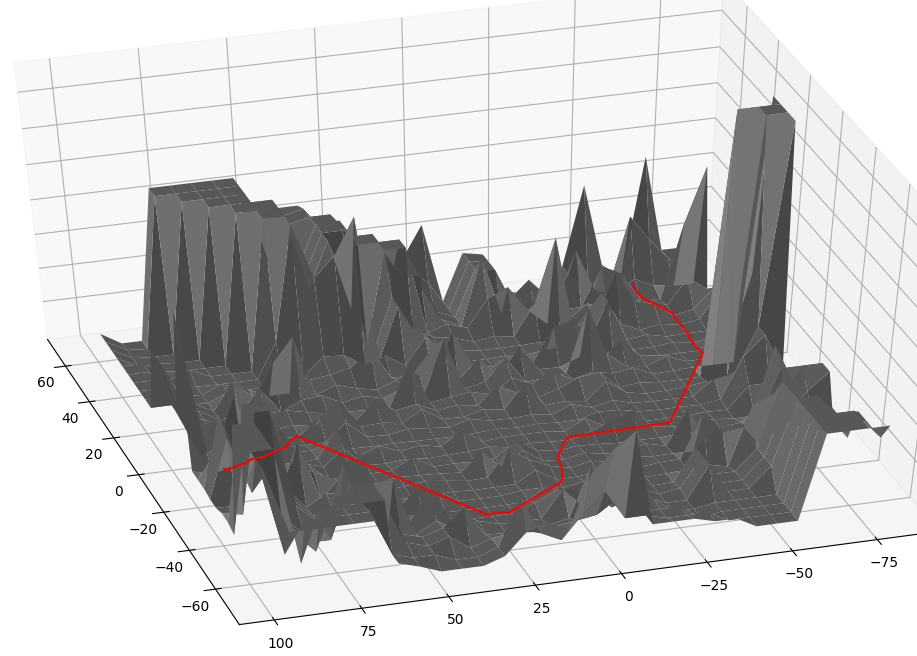
Interpolate Error Suface - PCA
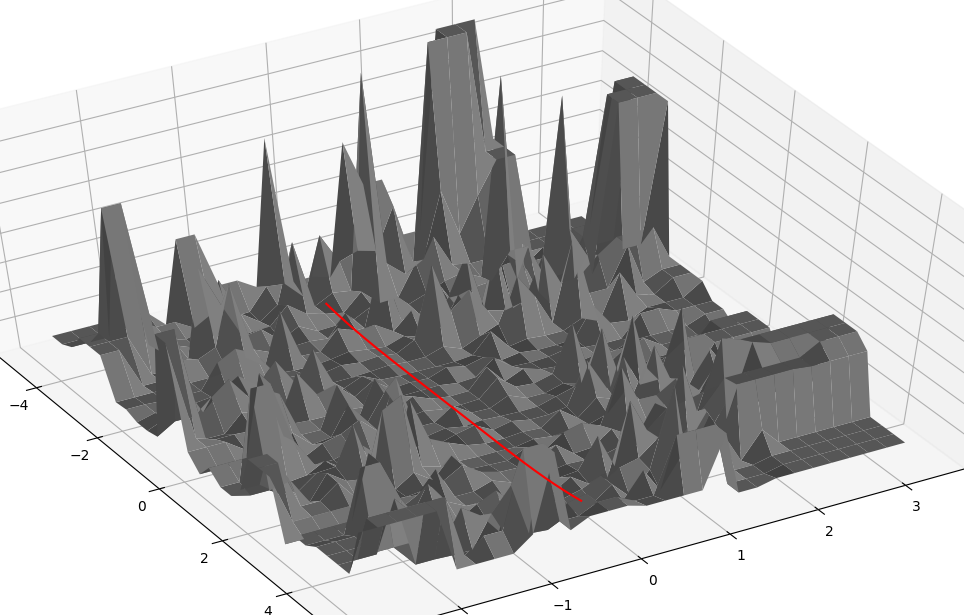
X_X
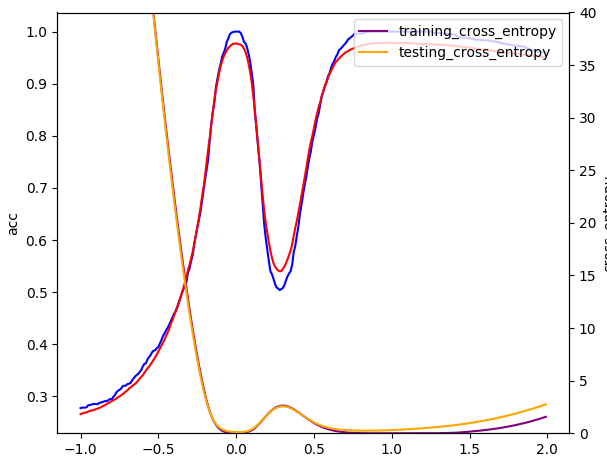
Really?
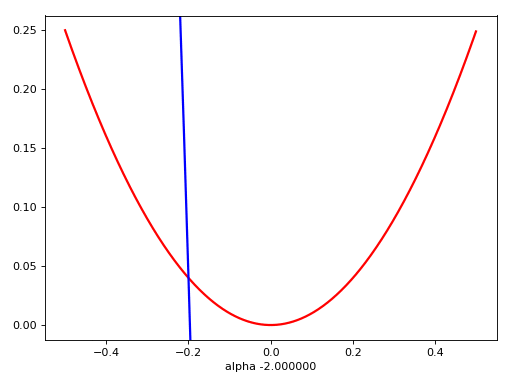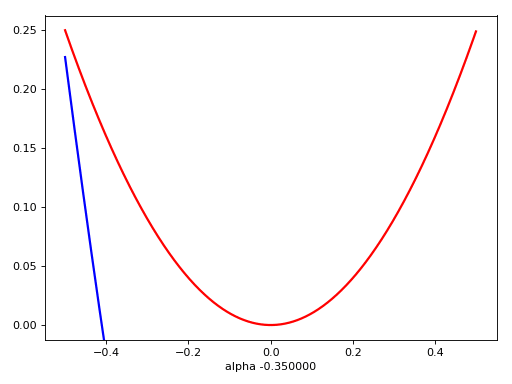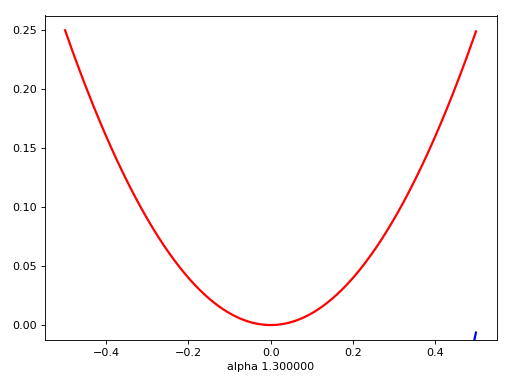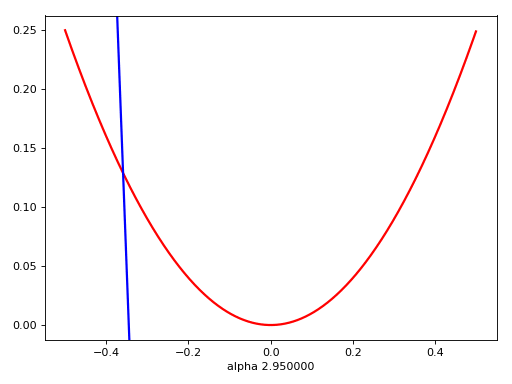
Flatness is False?
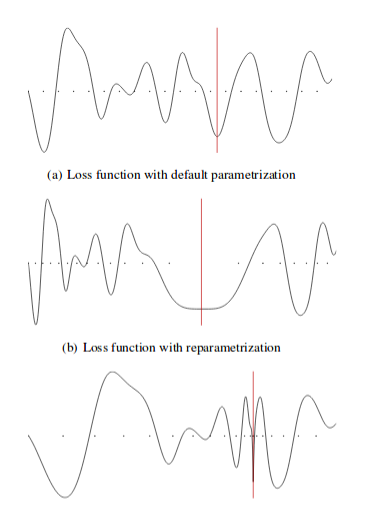
ACC != Loss
Flatness -x-> good minima
Maybe ...?
In highway..

S
w
w
w
w
w
S
S
S
S
老話一句:

Deep Learning 就是這麼神奇。
Indicator of Generalization-
Sensitivity
Why we need to know?
SGD + Momentum(or + Nesterov)
v.s.
Adam Family
Adam Family, e.g. Adam, Nadam, Adamax
solve local minima?
depends on data_noise?
U may be influenced by other hidden varibles.

How to solve it?
if dataset is too small....
Simulated annealing
(模擬退火)
What is the true story?
Before that...
他不是只有聽起來猛而已。
Can use in discrete problem!
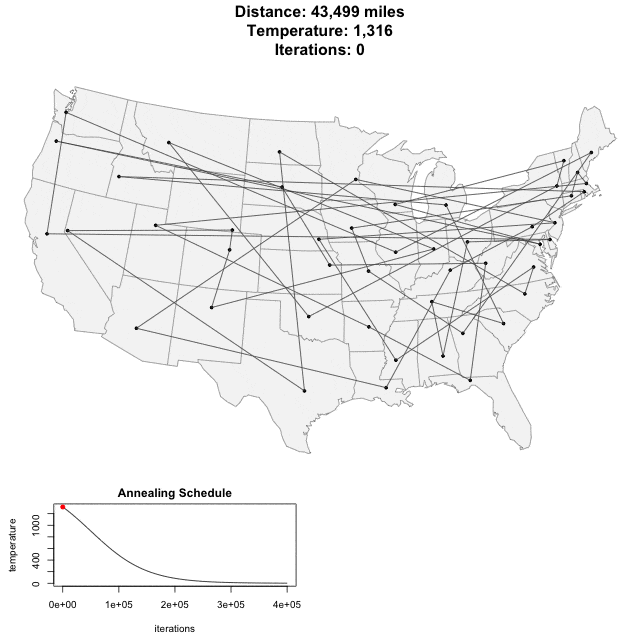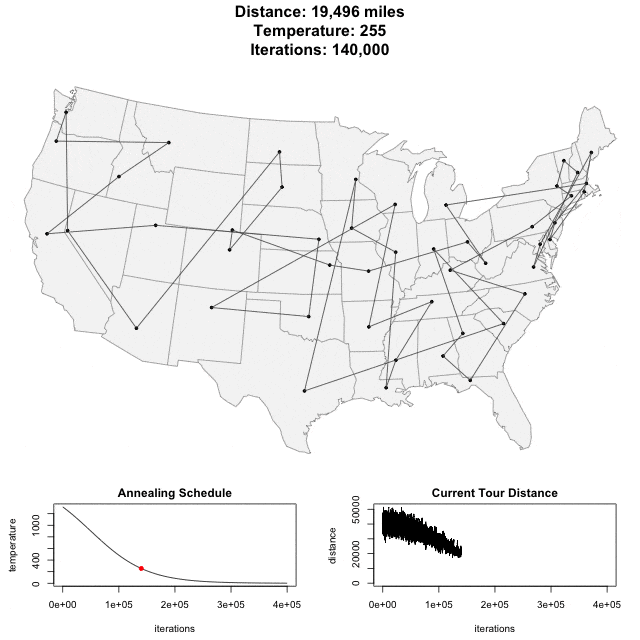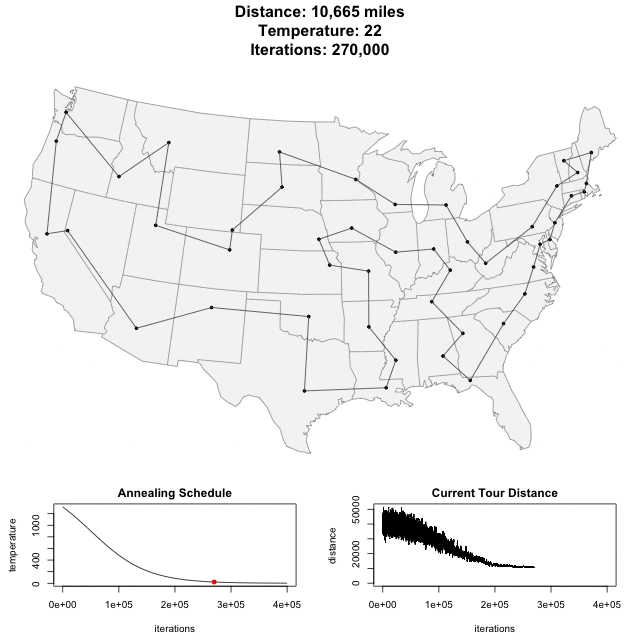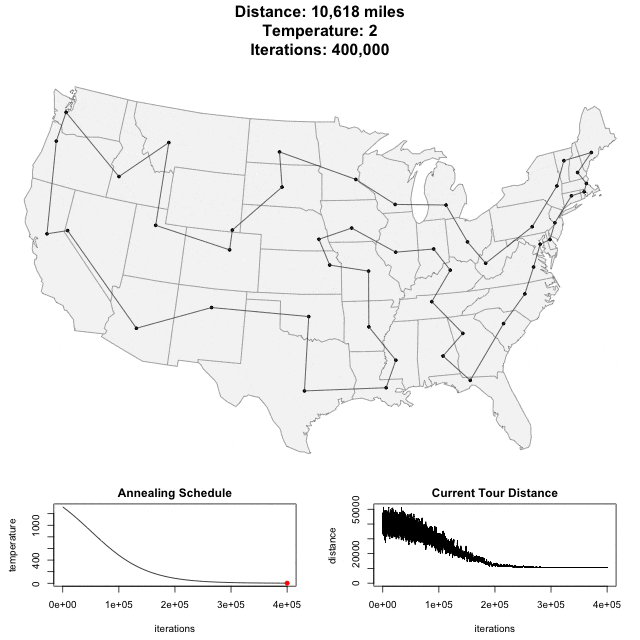
Simulated Annealing
Step1: Set initial x
Step2: x' = x + random()
Step3: change if P(x,x',T)
Step4: Repeated Step1-3.
Gradient Descent
Step by Step Explanation
Step1: Set initial state
Step2: x' = x + lr * GD
Step3: update x'
Step4: Repeated Step1-3.
When to Swap?
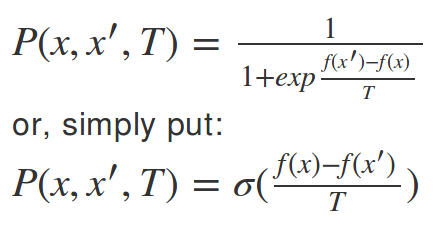
Temperature (T) = 5
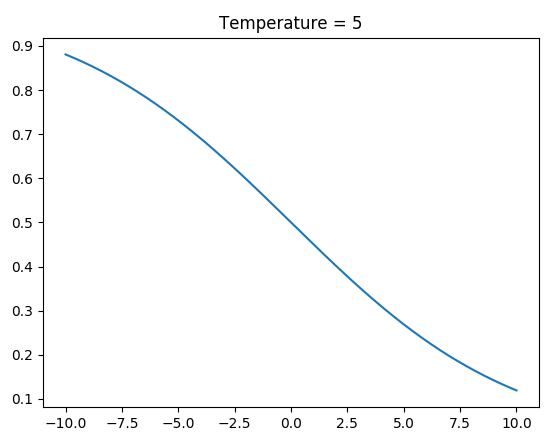
Temperature (T) = 1
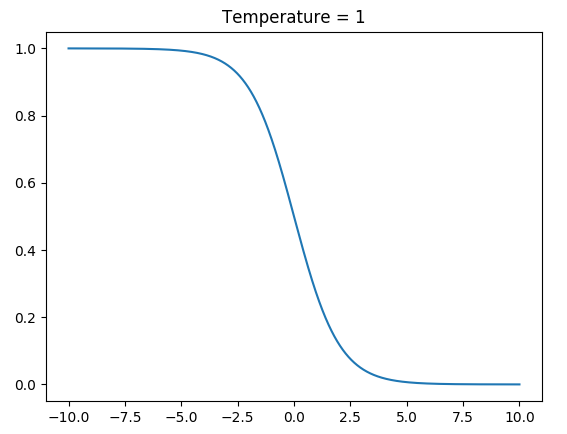
Power of Random
W...Why Still GD?
Doomsdays of Overfitting:
Gradient Noise
2. only SGD cannot beat the noise gradient:
https://openreview.net/pdf?id=rkjZ2Pcxe
1. Data augmentation v.s. Noise gradient ?
WOW! Mr. Keras!
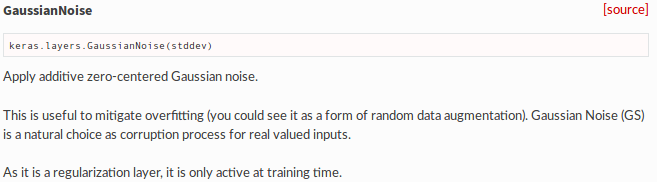
There is no convenient function in tensorflow & pytorch.
With Sharpness?
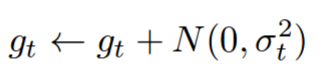
Noise Annealing
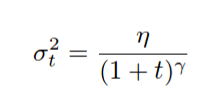
Performance - Noise/Dropout
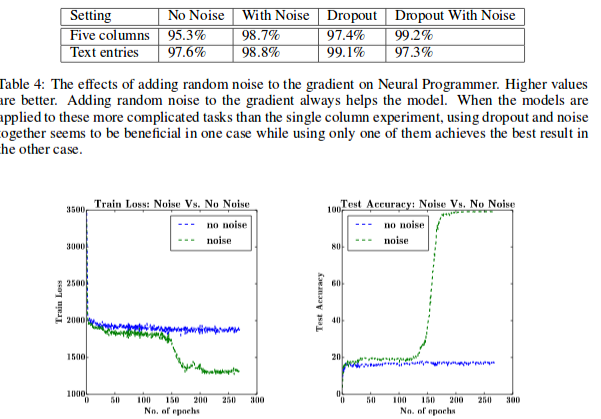
https://arxiv.org/pdf/1511.06807.pdf
Q&A?
