Time Complexity

Arvin Liu @ Sprout 2021

階段考TLE了啦 QQ...

階段考TLE了啦 QQ...

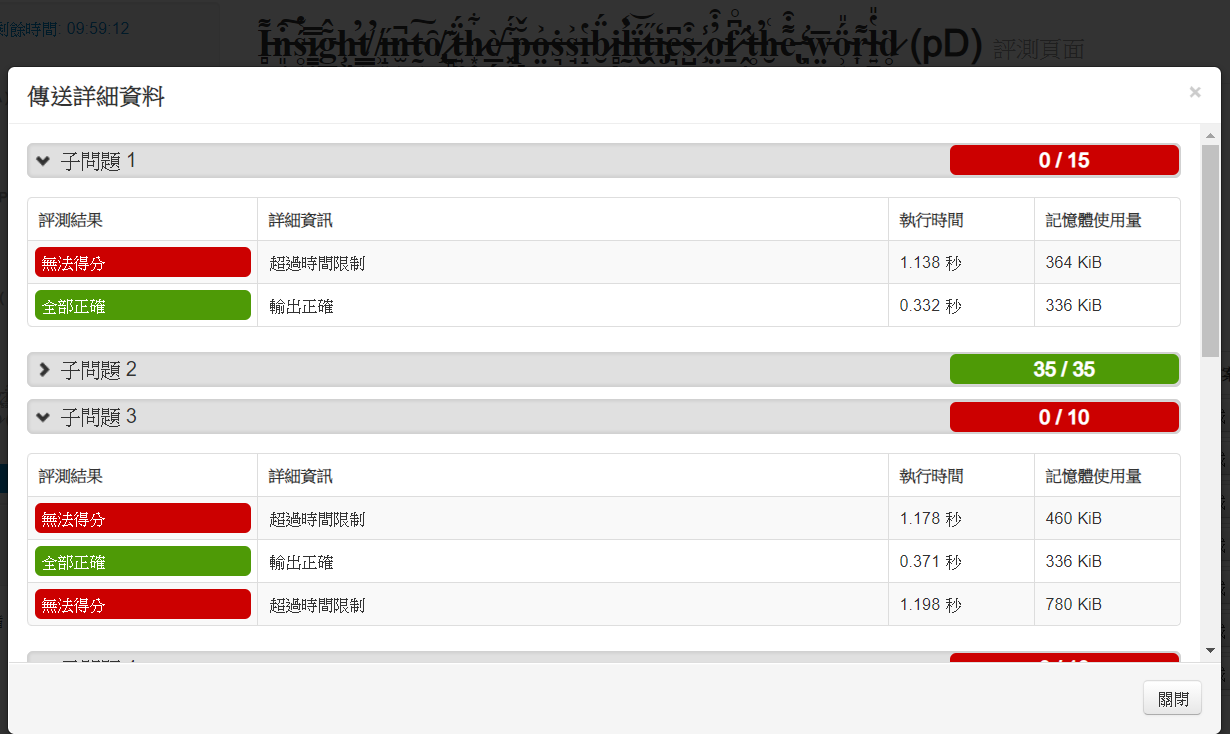
可不可以預判TLE呢?

要是能重來，我就不會浪費時間寫這題了>_<

預測時間

預測時間? 算算看指令數有多少

int n, sum = 0;
cin >> n;
for (int i=1; i<=n; i+=1)
  sum += i;
cout << sum;

宣告

3次

輸入輸出

2次

判斷 i <= n

+=

n, i, sum

cin >> n;

cin << sum;

n+1次

因為 i 會
從 1 跑到 n+1

2n次

因為 i+n次

sum也+n次

指令數量 : 3n + 6 次

預測時間? 算算看指令數有多少

int n;
cin >> n;
for(int i=1; i<=n; i++){
  for(int j=0; j<n-i; j++) cout << " ";
  for(int j=0; j<i; j++) cout << i;
  cout << " ";
  for(int j=0; j<i; j++) cout << i;
  cout << "\n";
}

指令數量 :                     次 

我也不知道

題目: 893 - 數字塔

去算那種枝微末節的指令數真的有用嗎?

誰算得出來==

當然，神如Jason就算得出來。

所以我們需要估計時間

指令數

n = 10
n = 10^3
n = 10^5
3n+6

大概是...

36
3006
300006
3n
\frac{n(n-1)}{2}
45
499500
4999950000
\frac 12 n^2
n \lceil \log_{10} n \rceil + n
20
4000
n \log_{10} n
110
1003000
10000500000
500000
n \lceil \log_{10} n \rceil + n^2
n^2

所以其實我們只要看最大的那一項就差不多了!

重看一次

int n;
cin >> n;
for(int i=1; i<=n; i++){
  for(int j=0; j<n-i; j++) cout << " ";
  for(int j=0; j<i; j++) cout << i;
  cout << " ";
  for(int j=0; j<i; j++) cout << i;
  cout << "\n";
}
n
n
n
\simeq 1.5 \times n^2 \text{次}

有沒有一個符號
表達估計指令數呢?

O

英文字母的第15個字

大O (big-Oh) 的定義

f(n) = Ο(g(n)) \leftrightarrow \\存在一個正常數c和n_0，\\\text{對於所有} n\ge n_0，\\ 使得f(n) \le c × g(n)。

看不懂? 沒關係。
就是取成長最快的項 再把係數拿掉就好了。

這裡的O，我們就稱之為複雜度，表示程式要跑多少次指令。

例如 100n^2 - 100000 n + 10 \log n + \pi \sqrt n = O(n^2)
f(n) = Ο(g(n)) \leftrightarrow 存在一個正常數c和n_0，\text{對於所有} n \ge n_0，\\ 使得f(n) \le c × g(n)。

 = 取成長最快的項 再把係數拿掉就好了。

指令數 時間複雜度
6
\overbrace{n+n+n+n+...+n}^n
n \lceil \log_{10} n \rceil + n
n \lceil \log_{10} n \rceil + n^2
O(1)
O(n^2)
O(n \log n)
O(n^2)
2^n + 3^n + n^{100}
O(3^n)
n \log \log n + 1000000 \times n
O(n \log \log n)
1 + \frac 12 + \frac 13 + \frac 14 + ... \frac 1n
O(\log n)
n + \frac n2 + \frac n4 + \frac n8 + ... + 1
O(n)

大O (big-Oh) 的定義

小小補充

n + \frac n2 + \frac n4 + \frac n8 + ... + 1 為甚麼是O(n) ?
它介於n \sim 2n-1之間 \rightarrow O(n)
\frac 12 + \frac 14 + \frac 18 + ... + \frac 1\infin = 1

小小補充-2

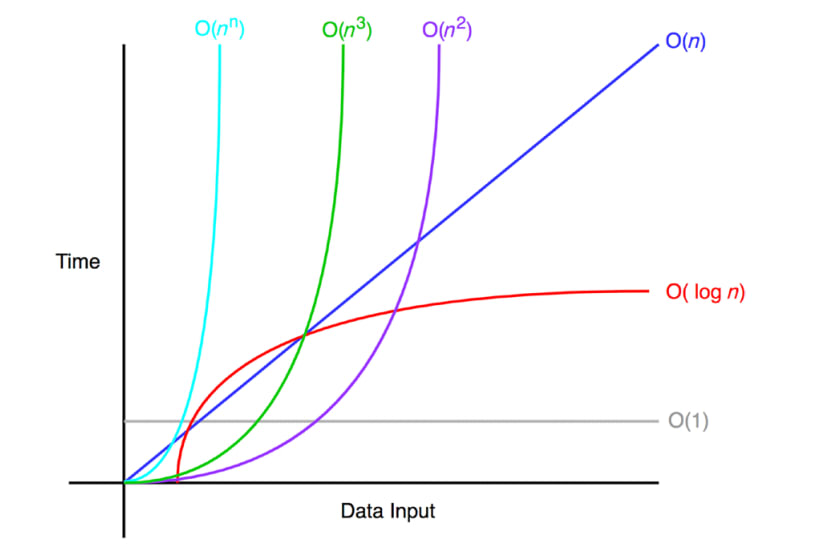
看起來好像很厲害的成長速率圖

所以那個TLE呢?

Got TLE?

Time Limit Exceeded

想一個解法

最差時間複雜度

計算code的指令數

TLE or 

... WA?

O(n\log n) \\ O(n^2)

估算
複雜度

代入測資

總而言之就是帶進去看有1秒沒有超過         就對了!

10^8
1s \le 10^8?

你還沒寫code啊，小老弟

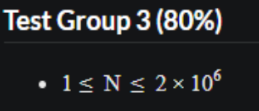
比較常看到的複雜度 - 範圍

時間複雜度 n 的範圍
O(n)
10^7, 10^8
O(n^2)
10^3, 5\times 10^3
O(n \sqrt n)
5 \times 10^4, 10^5
O(n \log n)
2 \times 10^6
O(1)
一個可以存的數字?

題外話:你怎麼念O(1)?

題外話:你怎麼念O(1)?

有if怎麼辦?

指令數可能每次都不一樣...

if (rand() % 2 == 0) {
  一個歐恩平方的函式();
} else {
  一個歐恩的函式();
}
一半O(n)，一半O(n^2)?

公O小?

很多的複雜度

最佳複雜度

最差複雜度

平均複雜度

什麼意思?

就...跑最快的時候啊

就...跑最慢的時候啊

就...平均的時候啊

期望值的次數

很多的複雜度

if (rand() % 2 == 0) {
  一個歐恩平方的函式();
} else {
  一個歐恩的函式();
}
哪種複雜度? 複雜度多少?
最佳複雜度
最差複雜度
平均複雜度
O(n)
O(n^2)
O(n^{1.5})

絕對不是             ，是

O(n^2)

偷渡一個排序 - Bogo Sort

排序是什麼? 就是把數字由小到大排。

什麼是Bogo Sort?

猴子表示: 要排序乾我?

Bogo Sort:
叫一隻猴子把
寫有數字的卡牌往空中一撒，
然後撿起來看順序對不對。

沒有? 再撒一次!

所以這個算法又稱猴子排序。

Bogo Sort 的複雜度?

哪種複雜度? 複雜度多少?
最佳複雜度
最差複雜度
平均複雜度
O(n)
O(\infin)
O(n \times n!)
is_sorted = False
while not is_sorted:
  shuffle(ary)       # O(n)
  if ary.is_sort():  # O(n)
    is_sorted = True # O(1)

shuffle:
洗牌/打亂順序

因為只有

\frac {1}{n!}

機率排對。

總而言之...

我們平常講O都是講最差複雜度，小心誤用。

O小好嗎?

一個奇怪的比較

指令數 時間複雜度
n
\frac{n(n-1)}{2}
10000000000 n
O(n)
O(n^2)
O(n)

平常情況下
10000000000 n 比 n*(n-1)/2 還要慢，

但是時間複雜度卻比較低。

O只是重要參考，但不代表真實情況(?)

Examples

一個你看過的例子

  • 假設說一開始的n個數字:
[1, 7, 11, 3, 5, 6, 9]
  • 那麼接下來詢問3次。
    • 詢問 2 -> 回答不存在。
    • 詢問 3 -> 回答存在。
    • 詢問 7 -> 回答存在。
題目:\\ 給n個數字，數字範圍在[0, M]之間。\\ 之後詢問Q次，每次詢問一個數字y。\\ 回答y在不在之前的n個數字裡面。

一個你看過的例子

一個最簡單但很慢解法:

用大小為n的陣列紀錄，每次詢問就用for看y在不在這個陣列裡面。

步驟 輸入到陣列 每次詢問 總共
最差複雜度 O(N) O(N) O(QN)
題目:\\ 給n個數字，數字範圍在[0, M]之間。\\ 之後詢問Q次，每次詢問一個數字y。\\ 回答y在不在之前的n個數字裡面。

一個你看過的例子

題目:\\ 給n個數字，數字範圍在[0, M]之間。\\ 之後詢問Q次，每次詢問一個數字y。\\ 回答y在不在之前的n個數字裡面。

一個有趣，很快的解法:

輸入x時讓陣列A[x] = true，
判斷時用A[y]決定有沒有出現過。

索引值 1 2 3 4 5 6 7 8 9
A裡面的值 T F T F F F T T F
假設輸入了 [1, 7, 3, 3, 1, 8]
步驟 清空A陣列 設定A陣列 每次詢問 總共
最差複雜度 O(M) O(N) O(1) O(M+N+Q)

一個你看過的例子

一個最簡單但很慢解法:

用大小為n的陣列紀錄，每次詢問就用for看y在不在這個陣列裡面。

一個有趣，很快的解法:

輸入x時讓陣列A[x] = true，
判斷時用A[y]決定有沒有出現過。

最差時間複雜度

O(QN)
O(N+M+Q)

你所想的算法

當\begin{cases} M \gt QN，用第一個算法。 \\ M \le QN，用第二個算法。 \end{cases}

結束啦!

騙你的(?)

還有喔?

步驟 排序
最差複雜度 O(NlogN)
題目:\\ 給n個數字，數字範圍在[0, M]之間。\\ 之後詢問Q次，每次詢問一個數字y。\\ 回答y在不在之前的n個數字裡面。

一個有趣，很快，不用管M的解法:

用大小為n的陣列排序，
再來用二分搜尋法判斷有沒有存在。

假設輸入了 [1, 7, 3, 3, 1, 8]
每次詢問 總共
O(logN) O((N+Q)logN)
排序後的值 1  1 3 3 7 8

小小整理

預處理 預處理時間複雜度 詢問 單次詢問時間複雜度 總時間複雜度
直接存起來 O(N) 一個一個比對 O(N) O(QN)
開一個陣列紀錄存過誰 O(N+M) 直接看紀錄陣列就好了 O(1) O(N+M+Q)
存起來後排序 O(NlogN) 二分搜尋法 O(logN) O((N+Q)logN)
題目:\\ 給n個數字，數字範圍在[0, M]之間。\\ 之後詢問Q次，每次詢問一個數字y。\\ 回答y在不在之前的n個數字裡面。

你還想的到其他算法嗎?

Made with Slides.com