Dr. Ashish Tendulkar

Machine Learning Techniques

IIT Madras

Models of Classification

Classification methods

  1. Discriminant functions learn direct mapping between feature vector \(\mathbf{x}\) and label \(y\).
  2. Generative and discriminative models learn conditional probability distribution \(p(y|\mathbf{x})\) and assigns label based on that.
    • Generative classifiers use Bayes theorem on class conditional densities \( p(\mathbf{x}|y)\) for features and prior probabilities of classes \(p(y)\).
    • Discriminative classifiers use parametric models.
  3. Instance based models compare the test examples with the training examples and assign class labels based on certain measure of similarity.

Part I: Classification setup

Classification set up

  • Predict class label \(y\) of an example based on the feature vector \(\mathbf{x}\).
  • Class label \(y\) is a discrete quantity unlike a real number in regression set up.

Nature of class label

  • Label is a discrete quantity - precisely an element in some finite set of class labels.
\begin{aligned} Y &= \{0, 1\} \\ Y &=\{-1, +1\} \\ Y &= \{\text{yes}, \text{no}\} \\ Y &= \{\text{apple}, \text{mango}, \text{banana}, \text{orange}\} \end{aligned}
  • Depending on the nature of the problem, we have one or more labels assigned to each example.

Types of classification

  1. Single label classification - where each example has exactly one label. 
    • e.g. is the applicant eligible for loan?
    • Label set: {yes, no}.
    • Label either yes or no.
  2. Multi-label classification - where each example has one or more labels.

    • e.g. identifying different types of fruits in a picture.

Label representation

  1. Single label classification: Label is a scalar quantity and is represented by \(y\).
  2. Multi-label classification: One or more labels hence vector representation \(\mathbf{y}\).
\mathbf{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_\color{blue}{k} \end{bmatrix}

Label set: \(Y = \{y_1, y_2, \ldots, y_k\}\) has \(k\) elements/labels.

Depending on the presence of the label, the corresponding label is set to 1.

Example: Single label classification (Binary)

  • Is the application eligible for loan?
  • Label set: \(\{yes, no\}\), usually converted to \(\{1, 0\}\)
    • Label: either \(yes\ (1)\) or \(no (0)\).
  • Training example:
    • Feature vector: \(\mathbf{x}\) - features for loan application like age of applicant, income, number of dependents etc.
    • Label: \(y\)

Example: Single label classification (Multiclass)

  • Types of iris flower
  • Label set: \(Y = \{versicolor, setosa, virginica\}\)
  • Label: exactly one label from set \(Y\).

Example: Single label classification (Multiclass)

  • Types of iris flower

versicolor

setosa

virginica

Image Source: Wikipedia.org

Label encoding in multiclass setup

Use one-hot encoding scheme for label encoding.

 

  • Make use of a vector \(\mathbf{y}\) with components equal to the number of labels in the label set.
  • In iris example, this would become:
\mathbf{y} = \begin{bmatrix} y_{versicolor} \\ y_{setosa} \\ y_{virginica} \\ \end{bmatrix}

Example: Label encoding (single label)

Let's assume that the flower has label versicolor, we will encode it as follows:

\mathbf{y} = \begin{bmatrix} y_{versicolor} = 1\\ y_{setosa} = 0\\ y_{virginica} = 0\\ \end{bmatrix}

Note that the component of \(\mathbf{y}\) corresponding to the label versicolor is 1, every other component is 0.

\mathbf{y} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}

Example: Multi-label Classification

  • Label all fruits from an image.
  • Label set: List of fruits e.g. \(\{apple,guava, mango, orange, banana, strawberry, \}\)
  • Label: One or more fruits as they are present in the image.
\mathbf{y} = \begin{bmatrix} y_{apple} \\ y_{guava} \\ y_{mango} \\ y_{orange} \\ y_{banana} \\ y_{strawberry} \\ \end{bmatrix}

Example: Multi-label Classification

Sample image

Image source: Wikipedia.org

Example: Multi-label Classification

Apple

Banana

Orange

Different fruits in the images are:

Example: Multi-label Classification

  • Let's assume that the labels are \(\mathbf{apple}\), \(\mathbf{orange}\) and \(\mathbf{banana}\).
\mathbf{y} = \begin{bmatrix} y_{apple} = 1\\ y_{guava} = 0\\ y_{mango} = 0\\ y_{orange} = 1\\ y_{banana} = 1\\ y_{strawberry} = 0\\ \end{bmatrix}
\mathbf{y} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0\\ \end{bmatrix}

becomes

Training Data: Binary Classification

  • Let's denote \(D\) as a set of \(n\)  pairs of a features vector \(\mathbf{x}_{m \times 1}\) and a label \(y\), to represent examples.
D = \left\{ (\mathbf{X}, \mathbf{y})\right\} = \left\{ (\mathbf{x}^{(i)}, y^{(i)})\right\}_{i=1}^{n}
  • \(\mathbf{X}\) is a feature matrix corresponding to all the training examples and has shape \(n \times m\).
    • In this matrix, each feature vector is transposed and represented as a row in this matrix. 

Training Data: Binary Classification

D = \left\{ (\mathbf{X}, \mathbf{y})\right\} = \left\{ (\mathbf{x}^{(i)}, y^{(i)})\right\}_{i=1}^{n}
\mathbf{X}_{n \times m} = \begin{bmatrix} - \left(x^{(1)}\right)^T - \\ - \left(x^{(2)}\right)^T - \\ \vdots \\ - \left(x^{(n)}\right)^T - \\ \end{bmatrix}

Concretely, the feature vector for \(i\)-th training example \(\mathbf{x}^{(i)}\) can be obtained by \(\mathbf{X}[i]\):

Training Data: Binary Classification

D = \left\{ (\mathbf{X}, \mathbf{y})\right\} = \left\{ (\mathbf{x}^{(i)}, y^{(i)})\right\}_{i=1}^{n}
\mathbf{y} = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)} \\ \end{bmatrix}
  • \(\mathbf{y}\) is a label vector of shape \(n \times 1\). 
  • The \(i\)-th entry in this vector gives label for \(i\)-th example, which is denoted by \(y^{(i)}\).

Training Data: Multi-class classification

D = \left\{ (\mathbf{X}, \mathbf{Y})\right\} = \left\{ (\mathbf{x}^{(i)}, \mathbf{y}^{(i)})\right\}_{i=1}^{n}

\(D\): Set of \(n\) pairs of a feature vector \(\mathbf{x}\) and a label vector \(\mathbf{y}\) representing examples.  

\mathbf{X}_{n \times m} = \begin{bmatrix} - \left(\mathbf{x}^{(1)}\right)^T - \\ - \left(\mathbf{x}^{(2)}\right)^T - \\ \vdots \\ - \left(\mathbf{x}^{(n)}\right)^T - \\ \end{bmatrix}

\(\mathbf{X}\) is an \(n \times m\) feature matrix.

\(\mathbf{Y}\) is a label matrix of shape \(n \times k\), where \(k\) is the total number of classes in label set.

\mathbf{Y} = \begin{bmatrix} - \left(\mathbf{y}^{(1)}\right)^T - \\ - \left(\mathbf{y}^{(2)}\right)^T - \\ \vdots \\ - \left(\mathbf{y}^{(n)}\right)^T - \\ \end{bmatrix}

Training Data: Multi-label classification

D = \left\{ (\mathbf{X}, \mathbf{Y})\right\} = \left\{ (\mathbf{x}^{(i)}, \mathbf{y}^{(i)})\right\}_{i=1}^{n}

\(D\): Set of \(n\) pairs of a feature vector \(\mathbf{x}\) and a label vector \(\mathbf{y}\) representing examples.  

\mathbf{X}_{n \times m} = \begin{bmatrix} - \left(\mathbf{x}^{(1)}\right)^T - \\ - \left(\mathbf{x}^{(2)}\right)^T - \\ \vdots \\ - \left(\mathbf{x}^{(n)}\right)^T - \\ \end{bmatrix}

\(\mathbf{X}\) is an \(n \times m\) feature matrix.

\(\mathbf{Y}\) is a label matrix of shape \(n \times k\), where \(k\) is the total number of classes in label set.

\mathbf{Y} = \begin{bmatrix} - \left(\mathbf{y}^{(1)}\right)^T - \\ - \left(\mathbf{y}^{(2)}\right)^T - \\ \vdots \\ - \left(\mathbf{y}^{(n)}\right)^T - \\ \end{bmatrix}

Multi-class and multi-label classification 

  • Multi-class classification: For \(\left(\mathbf{y}^{(i)}\right)^T\), exactly one entry corresponding to the class label is 1.
  • Multi-label classification: For \(\left(\mathbf{y}^{(i)}\right)^T\), more than one entries corresponding to the class labels can be 1.

Differs in the content of label vector

Part II: Discriminant Functions

Discriminant functions learn direct mapping between feature vector \(\mathbf{x}\) and label \(y\).

  \(\mathbf{x}\)                      Discriminant Function                             \(y\)

Model

In a binary classification set up with \(m\) features, the simplest discriminant function is very similar to the linear regression:

\begin{aligned} y &= w_0 + w_1 x_1 + \ldots + w_m x_m \\ &= w_0 + \mathbf{w}^T \mathbf{x} \end{aligned}

label

bias

weight vector

feature vector

Here label \(y\) is a discrete quantity unlike a real number in the linear regression set up.

Let's look at this discriminant function from geometric perspective.

Geometric Interpretation

Geometrically, the simplest discriminant function, \(y = w_0 + \mathbf{w}^T \mathbf{x}\) represents a hyperplane in \(m-1\) dimensional space where \(m\) is the number of features.

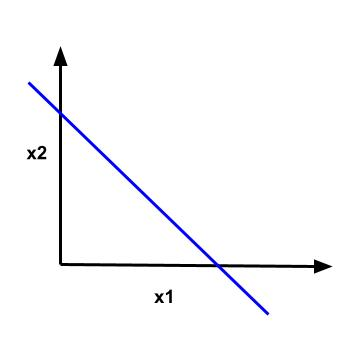
# features (m) Discriminant function 
1 Point
2 Line
3 Plane 
4 Hyperplane in 3D space
... ...
m Hyperplane in (m-1)-D space

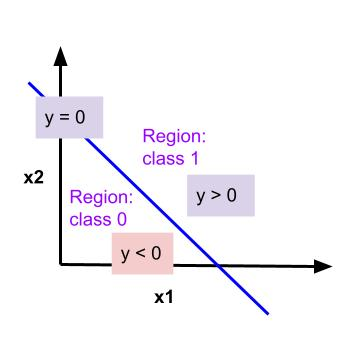
(m-1)-D hyperplane (which is line in this case) divides feature space into two regions one for each class:

  • Region for class 1, where \(y > 0\)
  • Region for class 2, where \(y < 0\)

The decision boundary between two classes is represented with (m-1)-D hyperplane: \(w_0 + \mathbf{w}^T\mathbf{x} =  0 \).

On decision boundary, \(y = 0\)

What does \(\mathbf{w}\) represent?

Consider two points \(\mathbf{x}^{(A)}\) and \(\mathbf{x}^{(B)}\) on the decision surface, we will have

\mathbf{w}^T (\mathbf{x}^{(A)} - \mathbf{x}^{(B)}) = 0
y^{(A)} = w_0 + \mathbf{w}^T \mathbf{x}^{(A)} = 0 \\ y^{(B)} = w_0 + \mathbf{w}^T \mathbf{x}^{(B)} = 0

Since \(y^{(A)} = y^{(B)} = 0\), \(y^{(A)} - y^{(B)}\) results into the following equation:

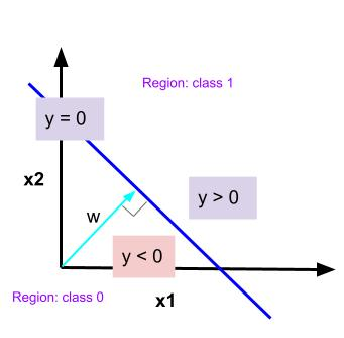
The vector \(\mathbf{w}\) is orthogonal to every vector lying within the decision surface, hence it determines the orientation of the decision surface.

\mathbf{w}^T (\mathbf{x}^{(A)} - \mathbf{x}^{(B)}) = 0

What does \(w_0\) represent?

For points on decision surface, we have

\begin{aligned} w_0 + \mathbf{w}^T \mathbf{x} &= 0 \\ \mathbf{w}^T \mathbf{x} &= - w_0 \\ \end{aligned}
\dfrac{\mathbf{w}^T \mathbf{x}}{||\mathbf{w}||} = - \dfrac{w_0}{||\mathbf{w}||}

Normalizing both sides with the length of the vector \(||\mathbf{w}||\), we get normal distance from the origin to the decision surface:

\(w_0\) determines the location of the decision surface

What does \(y\) represent?

\(y\) gives signed measure of perpendicular distance of the point \(\mathbf{x}\) from the decision surface.

Summary of geometric interpretation

  • \(w_0\) determines the location of the decision surface.
  • \(\mathbf{w}\) determines the orientation of the decision surface.
  • \(y\) gives signed measure of perpendicular distance of the point \(\mathbf{x}\) from the decision surface.
  • Decision surface divides feature space into two regions.

Now that we understand discriminant functions geometrically, let's explore how to classify an example \(\mathbf{x}\) with discriminant functions.

Inference

y =\left\{ \begin{aligned} 1, & \ \text{if}\ w_0 + \mathbf{w}^T \mathbf{x} > 0 \\ 0, & \ \text{otherwise} \end{aligned}\right. % y =\left\{ % \begin{array}{@{}ll@{}} % 1, & \text{if}\ w_0 + \mathbf{w}^T \mathbf{x} > 0 \\ % 0, & \text{otherwise} % \end{array}\right.

Discriminant function assigns label 1 to an example with feature vector \(\mathbf{x}\) if \((w_0 + \mathbf{w}^T\mathbf{x}) > 0 \) else assigns label 0.

Multiple classes

Assuming the number of classes to be \(k > 2\), we can build discriminant functions in two ways:

 

  • One-vs-rest: Build \(k-1\) discriminant functions. Each discriminant function solves two class classification problem: class \(c_k\) vs \(not \ c_k\).
  • One-vs-one: One discriminant function per pair of classes.  Total functions = \({k \choose 2} = \frac{k  (k-1)}{2}\)  

Issues with one-vs-rest

  • Each discriminant function separates \(C_k\) and not \(C_k\).
  • Region of ambiguity is in green.

Issues with one-vs-one

  • \(k(k-1)/2\) discriminant functions for each class pair \(C_i\) and \(C_j\).
  • Each discriminant function separates \(C_i\) and \(C_j\).
  • Each point is classified by majority vote.
  • Region of ambiguity is in green.

How do we fix it?

A single \(k\)-class discriminant comprising \(k\) linear functions as follows:

\begin{aligned} y_k &= w_{k0} + w_{k1} x_1 + \ldots + w_{km} x_m \\ &= w_{k0} + \mathbf{w_k}^T \mathbf{x} \end{aligned}
\begin{aligned} y_\color{blue}{1} &=& w_{\color{blue}{1}\color{black}{0}} + \mathbf{w_\color{blue}{1}}^T \mathbf{x} \\ y_\color{blue}{2} &=& w_{\color{blue}{2}\color{black}{0}} + \mathbf{w_\color{blue}{2}}^T \mathbf{x} \\ \vdots \\ y_\color{blue}{k} &=& w_{\color{blue}{k}\color{black}{0}} + \mathbf{w_\color{blue}{k}}^T \mathbf{x} \end{aligned}

Concretely:

Classification in \(k\)-discriminant functions

Assign label \(y_k\) to example \(\mathbf{x}\) if \(y_k > y_j, \forall j \ne k\)

\begin{aligned} {\color{red}(w_{k0} - w_{j0})} + {\color{blue}(\mathbf{w}_k - \mathbf{w}_j)^T} \mathbf{x} = 0 \end{aligned}

The decision boundary between classes \(y_k\) and \(y_j\) corresponds to \(m-1\) dimensional hyperplane:

This has the same form as the decision boundary for the two class cases:

{\color{red}w_0} + {\color{blue}\mathbf{w}^T} \mathbf{x} = 0

Now that we have a model of linear discriminant functions, we will study two approaches for learning the parameters of the model:

  • Least squares
  • Perceptron

Evaluation measures

  • Confusion matrix
  • Precision, recall, F1 scores, accuracy
  • AUC of ROC and PR curves

Least square classification

Least square classification adapts linear regression for classification.

We use least square error as a loss function.

Least square error

The error at \(i\)-th training point is calculated as follows:

\begin{aligned} e^{(i)} &= (\mathrm{\color{blue}{actual\ label} - \color{red}{predicted\ label}})^2 \\ &= \left (\color{blue}{y^{(i)}} - \color{red}{h_{\mathbf{w}}(\mathbf{x}^{(i)})} \color{black}\right)^2 \\ &= \left (\color{blue}{y^{(i)}} - \color{red}{\mathbf{w}^T \mathbf{x}^{(i)}} \color{black}\right)^2 \end{aligned}

The total loss is the sum of square of errors between actual and predicted labels at each training point.

\begin{aligned} J(\mathbf{w}) &= \sum_{i=1}^{n} e^{(i)} \\ &= \mathbf{e}^T\mathbf{e} \\ &= (\mathbf{y - Xw})^T (\mathbf{y - Xw}) \end{aligned}

Note that the loss is dependent on the value of \(\mathbf{w}\) - as these value changes, we get a new model, which will result in different prediction and hence affects the error at each training point.

Optimization

Normal equation

Calculate derivative of loss function \(J(\mathbf{w})\) w.r.t. weight vector \(\mathbf{w}\). [refer to linear regression material for detailed derivation]

\dfrac{\partial J(\mathbf{w})}{\partial \mathbf{w}} = 2(\mathbf{X}^T \mathbf{X} \mathbf{w} - \mathbf{X}^T \mathbf{y})

Set \(\dfrac{\partial J(\mathbf{w})}{\partial \mathbf{w}}\) to 0 and solve for \(\mathbf{w}\):

\begin{aligned} 2(\mathbf{X}^T \mathbf{X} \mathbf{w} - \mathbf{X}^T \mathbf{y}) &= 0\\ \mathbf{w} &= \left( \mathbf{X}^T \mathbf{X} \right)^{-1} \mathbf{X}^T \mathbf{y} \end{aligned}

Whenever \(\mathbf{X}^T \mathbf{X}\) is not full rank, we calculate pseudo-inverse: \(\left( \mathbf{X}^T \mathbf{X} \right)^{-1} \mathbf{X}^T\)

Gradient Descent

We derive weight update rule in vectorized format as follows:

\begin{aligned} \mathbf{w}_{k+1} &:= \mathbf{w}_k - \alpha \color{blue} {\frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}} \\ \mathbf{w}_{k+1} &:= \mathbf{w}_k - \alpha \color{blue} {\left(- 2 \mathbf{X}^T \mathbf{y} + 2 \mathbf{X}^T \mathbf{X} \mathbf{w}\right)} \\ \mathbf{w}_{k+1} &:= \mathbf{w}_k - \alpha \left( 2 \mathbf{X}^T \mathbf{X} \mathbf{w} - 2 \mathbf{X}^T \mathbf{y} \right) \end{aligned}

We will implement this update rule in gradient descent algorithm in colab.

Implementation from scratch and demo

def predict(X, w):
  z = X @ w
  return np.array([1 if z_val >= 0 else 0 for z_val in z]) 
def fit(X, y):
  return np.linalg.pinv(X) @ y

Inference

Optimization through normal equation

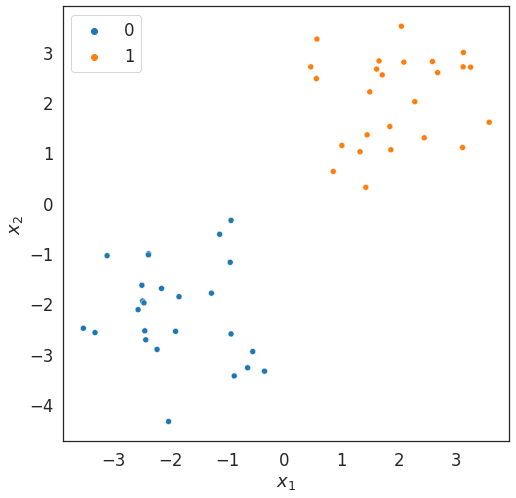
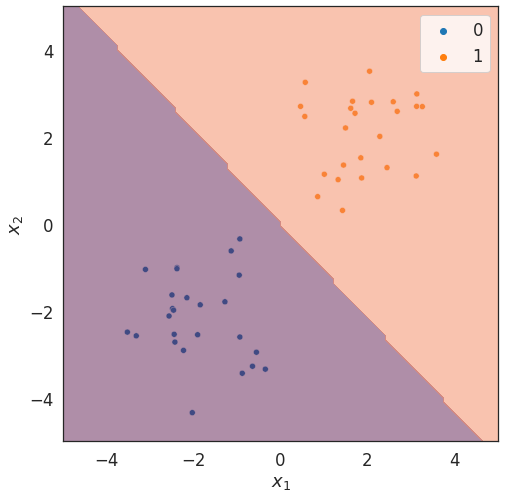
Training data

Decision boundary via LSC

Colab: Least square classification

Made with Slides.com