On Mutual Information Estimation
Too Boring; Didn't Watch
- Good black-box lower bounds on entropy are only possible when the entropy is small, otherwise require \(\color{red} \exp(H)\) samples
- Good black-box lower bounds on the Mutual Information are only possible when the MI is small, otherwise require \(\color{red} \exp(\text{MI})\) samples
- Good lower bounds are known when we know at least one marginal \(p(z)\)
- Good upper bounds are known when we know both \(p(x|z)\) and \(p(z)\) densities
- Alternative dependence measures might be interesting
Mutual Information
- A measure of dependence between two variables \(I(X, Z)\)
- \( I(X, Z) := H(Z) - H(Z|X) \)
- \( I(X, Z) := \text{KL}(p(x, z) \mid\mid p(x) p(z) ) \)
- Captures the idea of amount of "information" one r.v. carries about the other
Applications
- A natural measure of posterior collapse in VAEs $$\text{MI}[p_\theta(x,z)] = \mathbb{E}_{p_\theta(x)} \text{KL}(p_\theta(z|x) \mid\mid p(z))$$
- Representation Learning [2,3,4] $$ I(X, E_\theta(X)) \to \max_\theta $$
- Controlling dependence
- Demographic Parity in Fairness [17] $$ I(Y; C | X) = 0 $$
- Uncertainty Estimation
- Information Bottleneck [5]
- And more
Mutual Information Estimation
Lower bounds
| Unknown p(z) | Known p(z) | |
|---|---|---|
| Unknown p(x|z) | Hard | Doable |
| Known p(x|z) | Hard | Good |
Upper bounds
| Unknown p(z) | Known p(z) | |
|---|---|---|
| Unknown p(x|z) | Hard | Hard |
| Known p(x|z) | Doable | Good |
Black-box Lower Bounds
what are they good for?
Black-box Lower Bounds [6]
- \( I(X, Z) := \text{KL}(p(x, z) \mid\mid p(x) p(z) ) \)
- Can use lower bounds on KL
- Nguyen-Wainwright-Jordan (NWJ) [8] Lower Bound $$ \text{KL}(p(x) \mid\mid q(x)) \ge \mathbb{E}_{p(x)} f(x) - \mathbb{E}_{q(x)} \exp(f(x)) + 1 $$
- Donsker-Varadhan (DV) [7] Lower Bound $$ \text{KL}(p(x) \mid\mid q(x)) \ge \mathbb{E}_{p(x)} f(x) - \log \mathbb{E}_{q(x)} \exp(f(x)) $$
- InfoNCE [2] Lower Bound $$ \text{MI}[p(x, z)] \ge \mathbb{E}_{p(x, z_0)} \mathbb{E}_{p(z_{1:K})} \log \frac{\exp(f(x, z_0))}{\tfrac{1}{K+1} \sum_{k=0}^K \exp(f(x, z_k)) } $$
All these lower bounds have been shown to be very poor!
Formal Limitations [Unpublished]
Theorem [1]: Let \(B\) be any distribution-free high-confidence lower bound on \(\mathbb{H}[p(x)]\) computed from a sample \(x_{1:N} \sim p(x)\). More specifically, let \(B(x_{1:N}, \delta)\) be any real-valued function of a sample and a confidence parameter \(\delta\) such that for any \(p(x)\), with probability at least \((1 − \delta)\) over a draw of \(x_{1:N}\) from \(p(x)\), we have $$\mathbb{H}[p(x)] \ge B(x_{1:N}, δ).$$ For any such bound, and for \(N \ge 50\) and \(k \ge 2\), with probability at least \(1 − \delta − 1.01/k\) over the draw of \(x_{1:N}\) we have $$B(x_{1:N}, \delta) ≤ \log(2k N^2)$$
Good black-box lower bounds on \(\mathbb{H}\) require exponential number of samples!
$$ I(X, Z) = {\color{red} H(X)} - H(X|Z) \overset{\text{discrete } X}{\le} {\color{red} H(X)} $$
The NWJ Bound
- Recall the bound is: for any \(f(x)\) $$ \text{KL}(p(x) \mid\mid q(x)) \ge \mathbb{E}_{p(x)} f(x) - \mathbb{E}_{q(x)} \exp(f(x)) + 1 $$
- The optimal critic \(f(x)\) is $$ f^*(x) = \ln \tfrac{p(x)}{q(x)} $$
- The Monte Carlo estimate for \(x_{1:N}^{(p)} \sim p(x), x_{1:M}^{(q)} \sim q(x) \) and the optimal critic is $$ \frac{1}{N} \sum_{n=1}^N \ln \tfrac{p(x_n^{(p)})}{q(x_n^{(p)})} - \frac{1}{M} \sum_{m=1}^M \left[ \tfrac{p(x_m^{(q)})}{q(x_m^{(q)})} - 1 \right]$$
- The second term has zero expectation, but contributes variance $$ \text{Var}\left[ \frac{1}{M} \sum_{m=1}^M \left[ \tfrac{p(x_m^{(q)})}{q(x_m^{(q)})} - 1 \right] \right] = \frac{\chi^2(p(x) \mid\mid q(x))}{M} \ge \frac{\exp(\text{KL}(p(x) \mid\mid q(x))) - 1}{M}$$
- To drive the variance down one needs exponential number of samples \(M\)
The DV Bound
- Recall the bound is: for any \(f(x)\) $$ \text{KL}(p(x) \mid\mid q(x)) \ge \mathbb{E}_{p(x)} f(x) - \log \mathbb{E}_{q(x)} \exp(f(x)) $$
- The optimal critic \(f(x)\) is the same $$ f^*(x) = \ln \tfrac{p(x)}{q(x)} $$
- The Monte Carlo estimate for \(x_{1:N}^{(p)} \sim p(x), x_{1:M}^{(q)} \sim q(x) \) and the optimal critic is $$ \frac{1}{N} \sum_{n=1}^N \ln \tfrac{p(x_n^{(p)})}{q(x_n^{(p)})} - \log \left[ \frac{1}{M} \sum_{m=1}^M \tfrac{p(x_m^{(q)})}{q(x_m^{(q)})} \right]$$
- A biased estimate. The bias is non-negative and can be shown [10] to satisfy $$ \mathbb{E}_{q(x_{1:M})} \log \left[ \frac{1}{M} \sum_{m=1}^M \tfrac{p(x_m)}{q(x_m)} \right] = O\left( \text{Var}\left[ \frac{1}{M} \sum_{m=1}^M \tfrac{p(x_m^{(q)})}{q(x_m^{(q)})} \right] \right) $$
- To reduce the bias one'd need exponential number of samples \(M\)
The InfoNCE Bound
- Recall the bound is: for any \(f(x, z)\) $$ \text{MI}[p(x, z)] \ge \mathbb{E}_{p(x, z_0)} \mathbb{E}_{p(z_{1:K})} \log \frac{\exp(f(x, z_0))}{\tfrac{1}{K+1} \sum_{k=0}^K \exp(f(x, z_k)) } $$
- The optimal critic \( f^*(x, z) = \ln p(x|z) \)
- The bound can be shown to upper-bounded by \(\log (K+1)\): $$ \mathbb{E}_{p(x, z_0)} \mathbb{E}_{p(z_{1:K})} \log \frac{\exp(f(x, z_0))}{\tfrac{1}{K+1} \sum_{k=0}^K \exp(f(x, z_k)) } \le \log (K+1) $$
- Once again, one have to use exponential number of samples to have a good estimate of the MI
Example
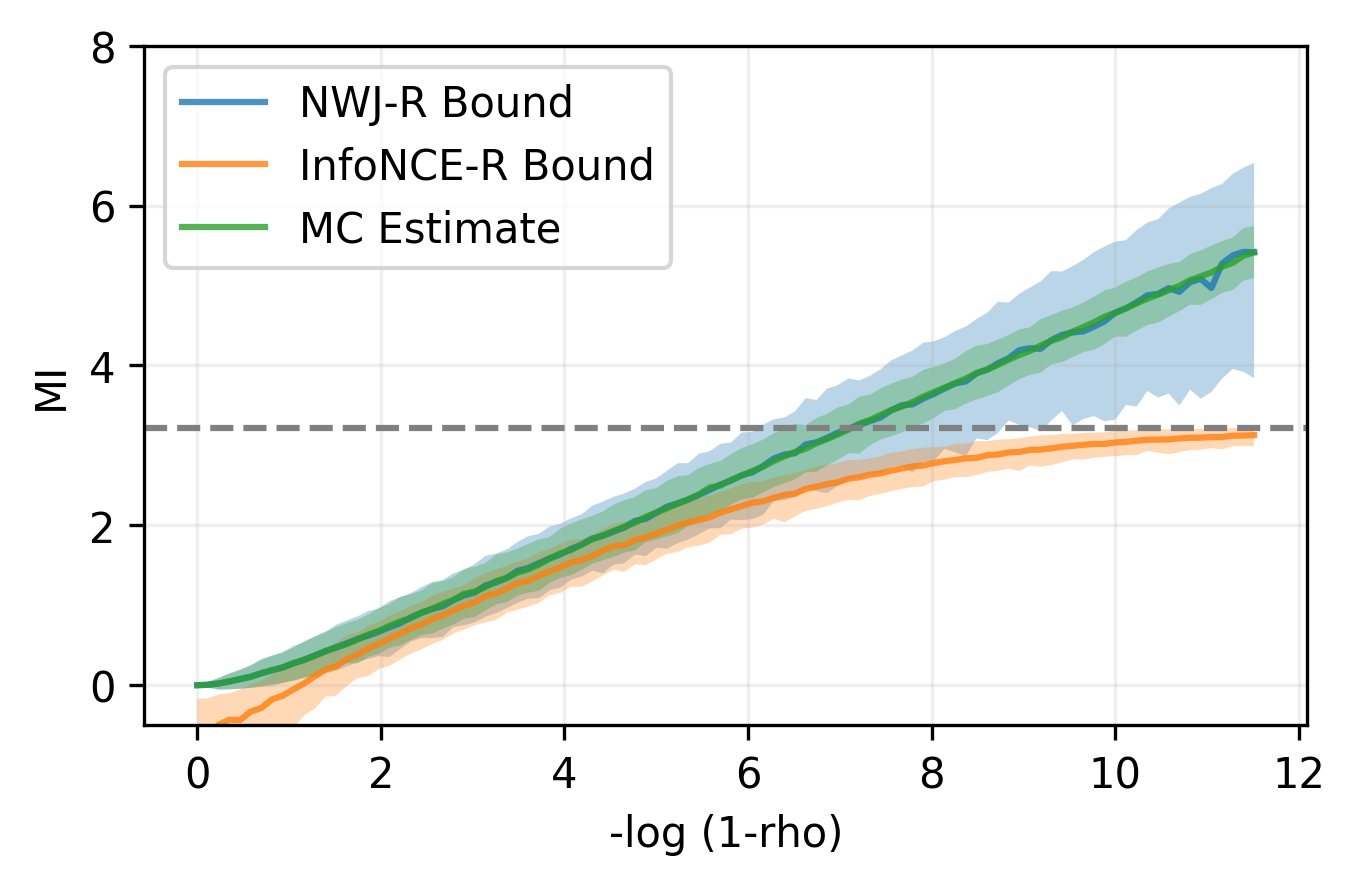
But why do they work?
- These methods have been reported to work empirically
- Despite negative results presented in this section
- "On Mutual Information Maximization for Representation Learning"
- Use MI to learn informative representations
- Tighter bounds do not translate into better representations
- Invertible representations keep improving
- Encoders initialized to be invertible become ill-conditioned
- Metric Learning seems to be a better interpretation
Does not agree with the MI-maximizing interpretation
Better Lower Bounds
by imposing more restrictions
Dissecting the Mutual Information
- Recall the equivalent definitions of the Mutual Information:
- \( \text{MI}[p(x, z)] := \text{KL}(p(x, z) \mid\mid p(x) p(z) ) \)
- \( \text{MI}[p(x, z)] := \mathbb{E}_{p(x, z)} \log p(x, z) - \mathbb{E}_{p(x)} \log p(x) - \mathbb{E}_{p(z)} \log p(z) \)
- \( \text{MI}[p(x, z)] := \mathbb{E}_{p(x, z)} \log p(z | x) - \mathbb{E}_{p(z)} \log p(z) \)
- \( \text{MI}[p(x, z)] := \mathbb{E}_{p(x, z)} \log p(x | z) - \mathbb{E}_{p(x)} \log p(x) \)
- Two ways to evade the dreadful Formal Limitations theorem:
- Avoid lower-bounding the intractable entropy
- Assume the marginal \(p(z)\) is known
Avoiding lower-bounds on entropies
- One of the equivalent definitions of the Mutual Information: $$ \text{MI}[p(x, z)] := \mathbb{E}_{p(x, z)} \log p(z | x) - \mathbb{E}_{p(z)} \log p(z) $$
- Assume the second term is tractable
- Upper-bound the conditional entropy
- Upper bounds are easy (and efficient): $$ 0 \le \text{KL}(p(x) \mid\mid q(x)) = \mathbb{E}_{p(x)} \log \tfrac{p(x)}{q(x)} \Rightarrow -\mathbb{E}_{p(x)} \log p(x) \le -\mathbb{E}_{p(x)} \log q(x) $$
- This leads us to the Barber-Agakov [9] lower bound on the MI: $$ \text{MI}[p(x, z)] \ge \mathbb{E}_{p(x, z)} \log q(z | x) - \mathbb{E}_{p(z)} \log p(z) $$
Assume the marginal is known
- Another equivalent definition of the Mutual Information: $$ \text{MI}[p(x, z)] := \mathbb{E}_{p(x, z)} \log p(x | z) - \mathbb{E}_{p(x)} \log p(x) $$
- Use known \(p(z)\) to lower-bound the second term
- Let \(\hat\rho(x,z)\) be any unnormalized pdf and \(q(z|x)\) be normalized
- IWHVI [12] upper bound + importance sampling: $$ \log p(x) \le \mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \log \tfrac{1}{K+1} \sum_{k=0}^K \frac{\rho(x, z_k)}{q(z_k|x)} + \text{KL}(p(x,z) \mid\mid \rho(x, z)) $$
- Hence $$ \boxed{ \mathbb{E}_{p(x, z)} \log \frac{p(x|z)}{p(x)} \ge \mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \log \frac{\hat\rho(x, z_0)}{\tfrac{1}{K+1} \sum_{k=0}^K \frac{\hat\rho(x, z_k)}{q(z_k|x)} } - \mathbb{E}_{p(z)} \log p(z) }$$
Multisample Lower Bound
$$ \text{MI}[p(x, z)] \ge \mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \log \frac{\hat\rho(x, z_0)}{\tfrac{1}{K+1} \sum_{k=0}^K \frac{\hat\rho(x, z_k)}{q(z_k|x)} } - \mathbb{E}_{p(z)} \log p(z)$$
- \(\hat\rho(x,z) \) approximates the joint distribution \(p(x,z)\)
- \(q(z|x)\) approximates the posterior distribution \(p(z|x)\)
-
For \(K=0\) we recover the Barber-Agakov lower bound
- Essentially, a fancy cross-entropy estimator for \(\log p(z|x)\)
- \(q(z|x)\) is enhanced by Self-Normalized Importance Sampling
-
\(q(z|x) = p(z)\) and \(\hat\rho(x, z) = \exp(f(x, z)) p(z) \) recover the InfoNCE lower bound
- Similar to SIVI [13]
- Explains its inefficiency due to poor choice of \(q(z|x)\)
Example
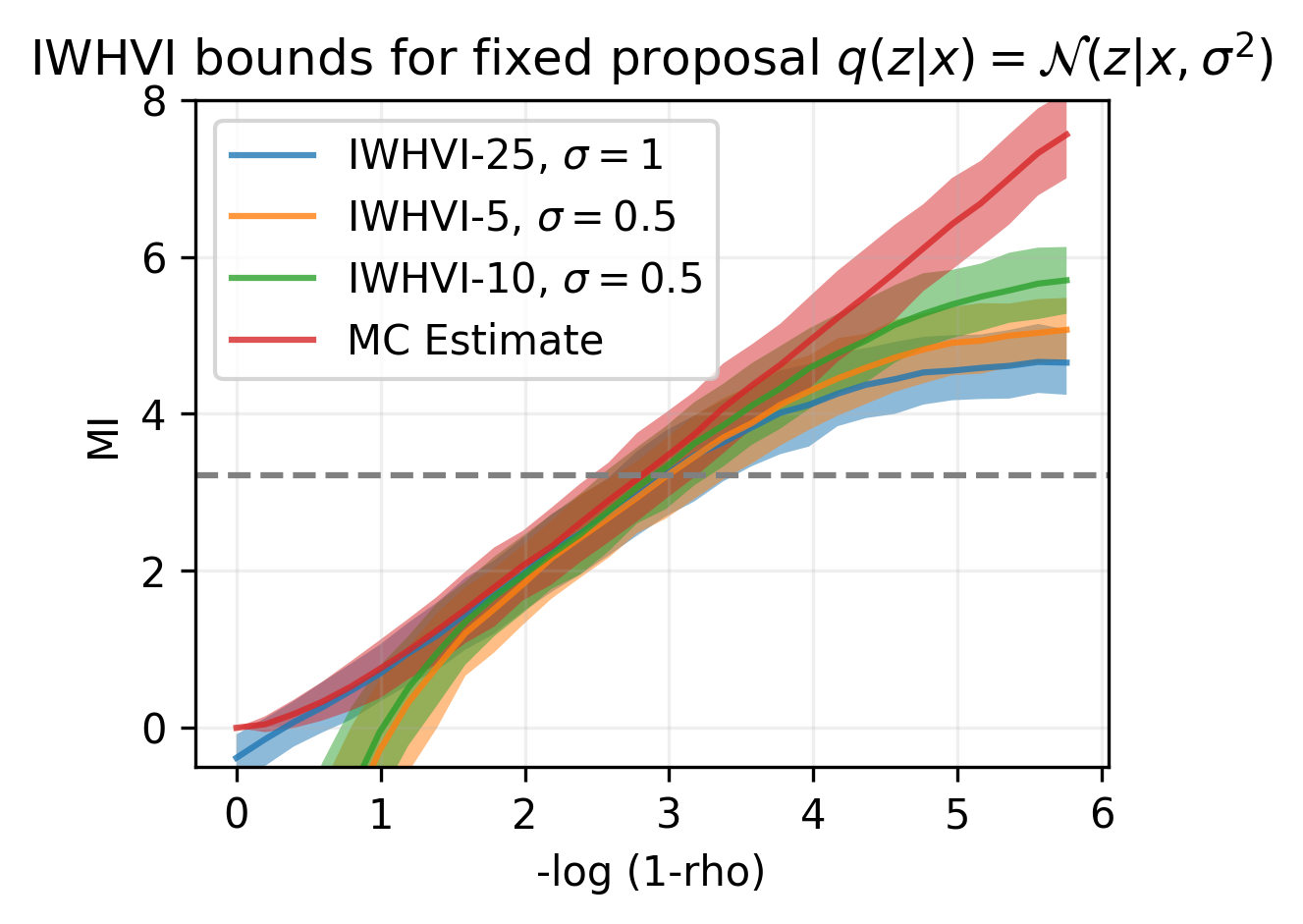
Upper Bounds
because sometimes we want to minimize
An Upper Bound on the Mutual Information
- Recall the equivalent definitions of the Mutual Information:
- \( I(X,Z) := H(X) - H(X|Z) = \mathbb{E}_{p(x, z)} \log p(x|z) - \mathbb{E}_{p(x)} \log p(x) \)
- Need a lower bound on the conditional entropy
- The theorem forbids any black-box efficient lower bounds
- Assume the conditional \(p(x|z)\) and the prior \(p(z)\) are known
- Can use IWAE [11] lower bound on \(\log p(x)\) to obtain the following upper bound: $$ \text{MI}[p(x,z)] \le \mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \frac{p(x|z_0)}{\tfrac{1}{K} \sum_{k=1}^K \tfrac{p(x,z_k)}{q(z_k|x)} } $$
- Where \(q(z|x)\) is a normalized variational distribution
- Putting \(q(z|x) = p(z) \) frees us from knowing the prior density \(p(z)\) $$ \text{MI}[p(x,z)] \le \mathbb{E}_{p(x, z_0)} \mathbb{E}_{p(z_{1:K})} \frac{p(x|z_0)}{\tfrac{1}{K} \sum_{k=1}^K p(x|z_k) } $$
A Sandwich Bound on the MI
$$\mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \frac{p(x|z_0)}{\tfrac{1}{K+1} \sum_{k=0}^K \tfrac{p(x,z_k)}{q(z_k|x)} } \le \text{MI}[p(x,z)] \le \mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \frac{p(x|z_0)}{\tfrac{1}{K} \sum_{k=1}^K \tfrac{p(x,z_k)}{q(z_k|x)} } $$
- A multisample variational sandwich bound
- Variational distribution \(q(z|x)\) approximates the true posterior \(p(z|x)\)
- \(K\) samples are used to improve the variational approximation
Alternative Dependency Measures
because the MI is not ideal
Alternative Measures
- Once again, the Mutual Information is:
$$ \text{MI}[p(x,z)] := \text{KL}(p(x,z) \mid\mid p(x)p(z) ) $$
- Has information-theoretic interpretation
- Suffers from inability to efficiently lower-bound the entropy
- One might consider other divergences between \(p(x,z)\) and \(p(x) p(z)\):
- Reverse KL: \( \text{KL}(p(x)p(z) \mid\mid p(x,z)) \)
- Any \(f\)-divergence: \( D_f(p(x,z) \mid\mid p(x)p(z)) \)
- \(p\)-Wasserstein: \(W_p( p(x,z) \mid\mid p(x)p(z) ) \) [14]
- (Seem to) Lack information-theoretic interpretation
Lautum Information
- While the Mutual Information is $$ \text{MI}[p(x,z)] := \text{KL}(p(x,z) \mid\mid p(x)p(z) ) $$
- The Lautum Information[15] is defined as $$ \text{LI}[p(x,z)] := \text{KL}(p(x)p(z) \mid\mid p(x, z) ) $$
-
\(\text{LI}[p(x,z)] = \mathbb{E}_{p(x)p(z)} \log \frac{p(x)}{p(x|z)} = -\mathbb{E}_{p(x)p(z)} \log p(x|z) -\mathbb{H}[p(x)] \)
- Lacks information-theoretic interpretation
- The entropy term allows some bounds
- Good black-box cross-entropy upper bounds
- Good distribution-dependent lower bounds
- The cross-entropy term is hard to deal with
Lower Bounds on the Lautum Information
- Recall the Lautum Information $$ \text{LI}[p(x,z)] = \mathbb{E}_{p(x)} \log p(x) - \mathbb{E}_{p(x)p(z)} \log p(x|z)$$
-
Simple cross-entropy lower bound: $$ \text{LI}[p(x,z)] \ge \mathbb{E}_{p(x)} \log q(x) - \mathbb{E}_{p(x)p(z)} \log p(x|z)$$
- Requires expressive tractable \(q(x)\)
-
Hierarchical multisample cross-entropy lower bound, \(q(x) := \int p(x|z) \rho(z) dz\): $$ \text{LI}[p(x,z)] \ge \mathbb{E}_{p(x)} \mathbb{E}_{q(z_{1:K}|x)} \log \frac{1}{K} \sum_{k=1}^K \frac{p(x|z_k) \rho(z_k)}{q(z_k|x)} - \mathbb{E}_{p(x)p(z)} \log p(x|z)$$
- \(\rho(z)\) approximates the marginal \(p(z)\)
- \(q(z|x)\) approximates the posterior \(p(z|x)\)
Upper Bounds on the Lautum Information
- The Lautum Information $$ \text{LI}[p(x,z)] = \mathbb{E}_{p(x)} \log p(x) - \mathbb{E}_{p(x)p(z)} \log p(x|z)$$
- No efficient lower bounds on the entropy unless we know \(p(z)\)
- IWHVI bound gives $$ \text{LI}[p(x,z)] \le \mathbb{E}_{p(x, z_0)} \mathbb{E}_{q(z_{1:K}|x)} \log \frac{1}{K+1} \sum_{k=0}^K \frac{p(x, z_k)}{q(z_k|x)} - \mathbb{E}_{p(x)p(z)} \log p(x|z)$$
- \(q(z|x)\) approximates the posterior \(p(z|x)\)
AIS-based Bounds
- All bounds we've considered essentially followed from lower and upper bounds on marginal log-likelihood given by Self-Normalized Importance Sampling (SNIS)
- Alternatively, one might consider Annealed Importance Sampling (AIS) [16]
- SNIS and AIS can be seen as non-parametric procedures that improve \(q(z|x)\)
- SNIS tries \(K\) different samples and selects the best-looking one
- Embarrassingly parallel
- Works with discrete random variables
- AIS takes a sample and runs several steps of HMC to move it towards \(p(z|x)\)
- Potentially more efficient in high-dimensional spaces
- Gradient-based MCMC only works in continuous spaces
- Sequential in nature
- SNIS tries \(K\) different samples and selects the best-looking one
Conclusion
- The MI is hard to estimate reliably in a black-box case
- Because the entropy is hard to estimate
- Black-box lower bounds on KL are bad for the same reason
- Knowing a marginal distribution \(p(z)\) enables efficient lower bounds
- Knowing the full joint distribution \(p(x,z)\) enables efficient upper bounds
- These bounds can be made tighter by using more computation
- We've developed SNIS-based bounds, AIS is also promising
- Alternative measures of dependency might not suffer from the entropy estimation problem
- As usual, for more see my blog
References
[1]: David McAllester, Karl Stratos. Formal Limitations on the Measurement of Mutual Information.
[2]: Aaron van den Oord, Yazhe Li, Oriol Vinyals. Representation Learning with Contrastive Predictive Coding.
[3]: R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, Yoshua Bengio. Learning deep representations by mutual information estimation and maximization.
[4]: Philip Bachman, R Devon Hjelm, William Buchwalter. Learning Representations by Maximizing Mutual Information Across Views.
[5]: Naftali Tishby, Noga Zaslavsky. Deep Learning and the Information Bottleneck Principle.
[6]: Ben Poole, Sherjil Ozair, Aaron van den Oord, Alexander A. Alemi, George Tucker. On Variational Bounds of Mutual Information.
[7]: Donsker, M. D. and Varadhan, S. S. Asymptotic evaluation of certain markov process expectations for large time.
[8]: Nguyen, X., Wainwright, M. J., and Jordan, M. I. Estimating divergence functionals and the likelihood ratio by convex risk minimization.
[9]: Barber, D. and Agakov, F. The im algorithm: A variational approach to information maximization.
[10]: Justin Domke, Daniel Sheldon. Importance Weighting and Variational Inference.
[11]: Yuri Burda, Roger Grosse, Ruslan Salakhutdinov. Importance Weighted Autoencoders.
[12]: Artem Sobolev, Dmitry Vetrov. Importance Weighted Hierarchical Variational Inference.
[13]: Mingzhang Yin, Mingyuan Zhou. Semi-Implicit Variational Inference.
[14]: Sherjil Ozair, Corey Lynch, Yoshua Bengio, Aaron van den Oord, Sergey Levine, Pierre Sermanet. Wasserstein Dependency Measure for Representation Learning.
[15]: Daniel P. Palomar, Sergio Verdu. Lautum Information.
[16]: Roger B. Grosse, Zoubin Ghahramani, Ryan P. Adams. Sandwiching the marginal likelihood using bidirectional Monte Carlo.
[17]: AmirEmad Ghassami, Sajad Khodadadian, Negar Kiyavash. Fairness in Supervised Learning: An Information Theoretic Approach.