Thoughts on linear types and compilers

Arnaud Spiwack

Pure languages

f :: a -> b -- A mathematical function
f x = … 
  -- Can't mutate x
  -- Can't read a file
  -- Can't print on stdout

Common subexpressions

Both are the same

Inlining

f x = e

…
f u
…

f x = e

…
e[x\u]
…

SSA is kind of about purity

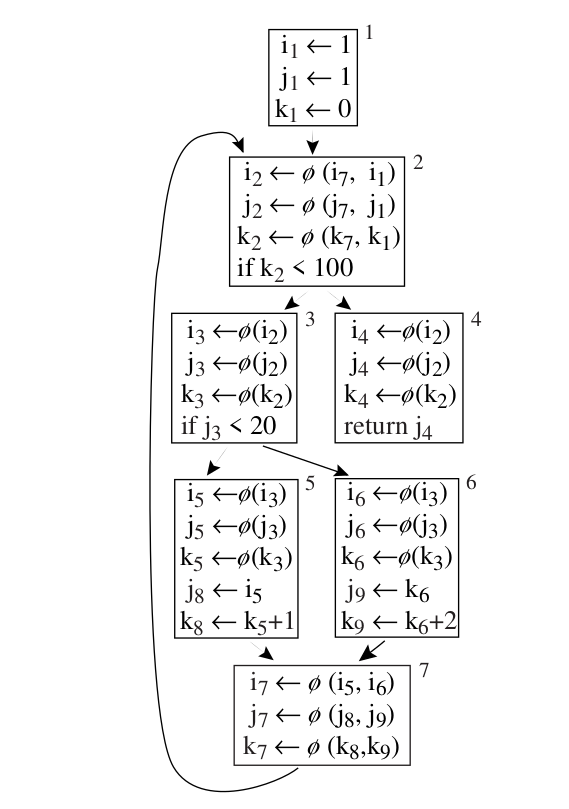
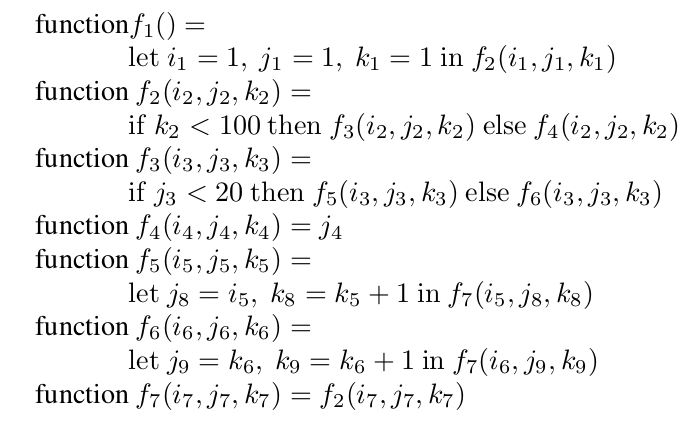
SSA is Functional Programming — Andrew Appel

\approx

Linear types

{-# LANGUAGE LinearTypes #-}

f :: a ⊸ b
f x = … -- consumes x exactly once

Since GHC 9.0

Linear types, by examples (1/3)

id x = x

✓

linear

dup x = (x,x)

✗

not linear

swap (x,y) = (y,x)

✓

linear

forget x = ()

✗

not linear

Linear types, by examples (2/3)

f (Left x) = x
f (Right y) = y

✓

linear

✓

linear

✗

not linear

h x b = case b of
  True -> x
  False -> x

g z = case z of
  Left x -> x
  Right y -> y

k x b = case b of
  True -> x
  False -> ()

✓

linear

Linear types, by examples (3/3)

f x = dup x

✓

linear

✗

not linear

h u = u 0

g x = id (id x)

k u = u (u 0)

✓

linear

✗

not linear

Mutable arrays

Linear Haskell — Bernardy, Boespflug, Newton, Peyton Jones, Spiwack

IO Monad

type IO a = RealWorld™ -> (a, RealWorld™)


readLine :: Handle -> IO String

type IO a = RealWorld™ ⊸  (a, RealWorld™)


readLine :: Handle -> IO String

Abstract machines

\langle c | \kappa \rangle

Code

Stack

Continuation-passing(ish)

Seel also A dissection of L — Arnaud spiwack

\begin{array}{lcl} u\,v & \leadsto & \mu(\kappa).\,\langle u | v \cdot \kappa \rangle \\[3mm] \lambda x.\,u & \leadsto & \mu(v \cdot \kappa).\,\langle u[x\mapsto v] | \kappa \rangle \end{array}

https://slides.com/aspiwack/edinburgh-201103

https://www.tweag.io/blog/tags/linear-types/