Linearly Qualified Types
Arnaud Spiwack, Csongor Kiss,
Jean-Philippe Bernardy, Nicolas Wu,
Richard A. Eisenberg

Generic Inference for Capabilities and Uniqueness
Linear Haskell
Design sketch
2017
2018
POPL paper
Merged in GHC
2020
2021
GHC 9.0.1 released
Today
2022
Linear Haskell 101
A -> BA %1 -> B(plus polymorphism stuff, but not for today)
Regular function
Linear function
If the result is consumed exactly once, the argument is consumed exactly once
Pure mutable arrays
swap :: Int -> Int -> MArray a %1 -> MArray A
swap i j as =
let
!(as', Ur ai) = get i as
!(as'', Ur aj) = get j as'
as''' = set i aj as''
as'''' = set j ai as'''
in
as''''val swap : [a] duplicable a
=> (i: int, j: int, as: marray a) -> () =
let ai = get (as, i) in
let aj = get (as, j) in
set (as, i, aj);
set (as, j, ai)Mezzo
Haskell
Constraints
nub :: Eq a => [a] -> [a]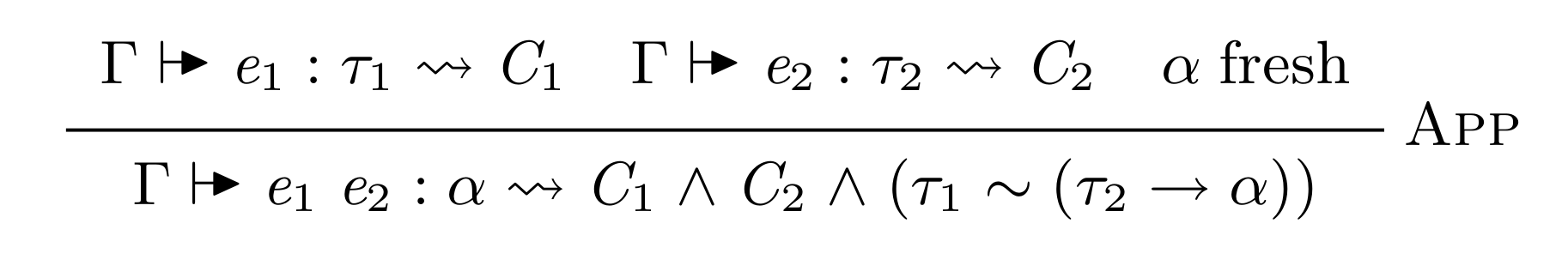
Constraints
Linear Constraint
set :: RW n %1 => Int -> a -> MArra…swap :: RW n %1 => Int -> Int -> MArray n a -> () ⧀ RW n
swap i j as =
let
!Ur ai = get i as
!Ur aj = get j as
!() = set i aj as
!() = set j ai as
in
()Scope functions
newMArray :: Int -> (MArray a %1 -> Ur b) %1 -> Ur bfromList :: [a] -> Array a
fromList as =
unUr $ newMArray (length as) $ \arr ->
let arr' = foldr (uncurry set) (zip [1..] as) arr in
freeze arr'
Linearly constraint
newMArray :: Linearly %1 => Int -> MArray afromList :: Linearly %1 => [a] -> Array a
fromList as =
let arr = newArray (length as) in
let arr' = foldr (uncurry set) (zip [1..] as) arr in
unUr $ freeze arr'
Draw the rest of the owl
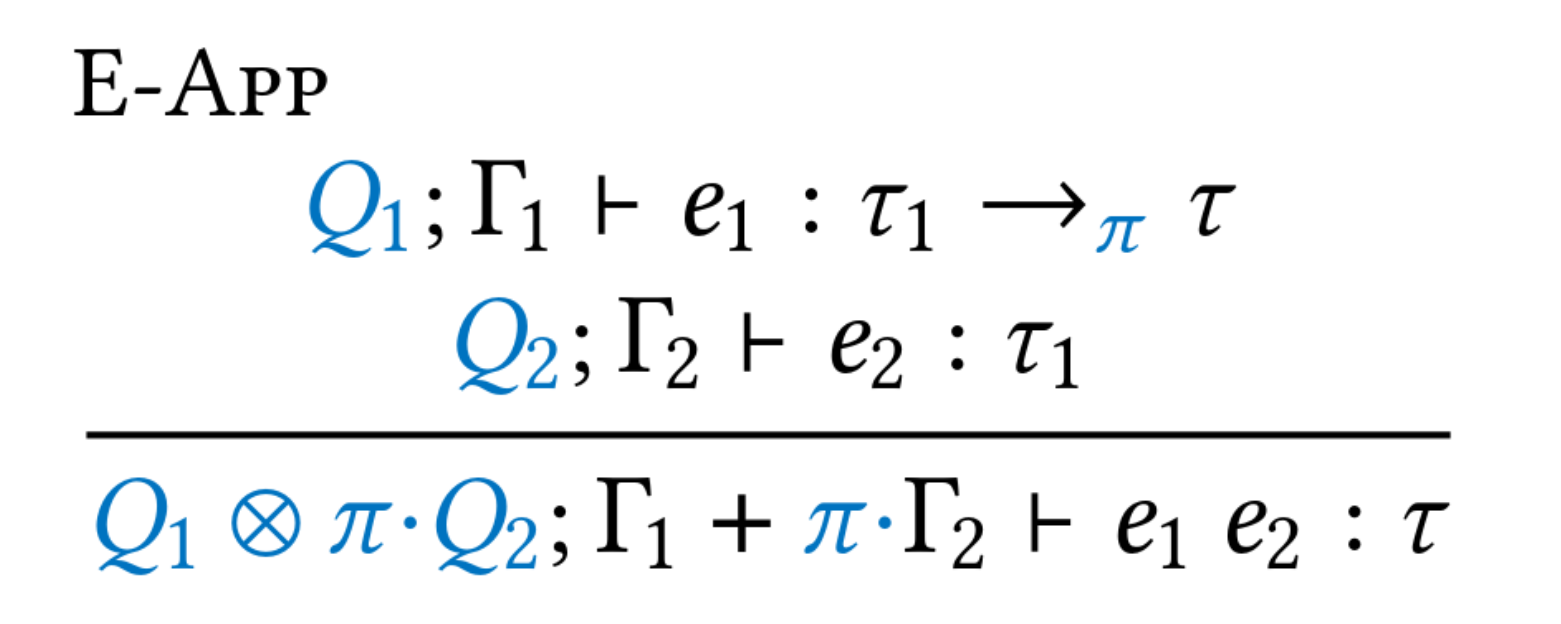
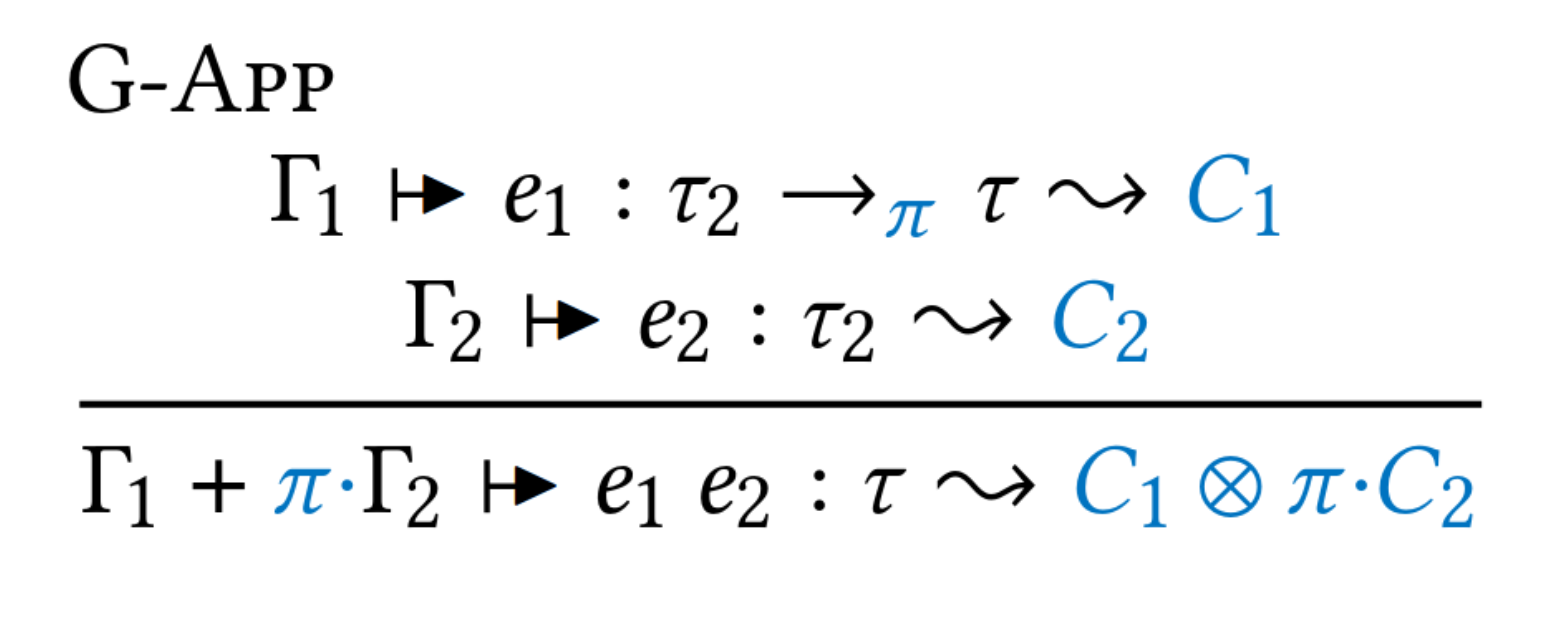
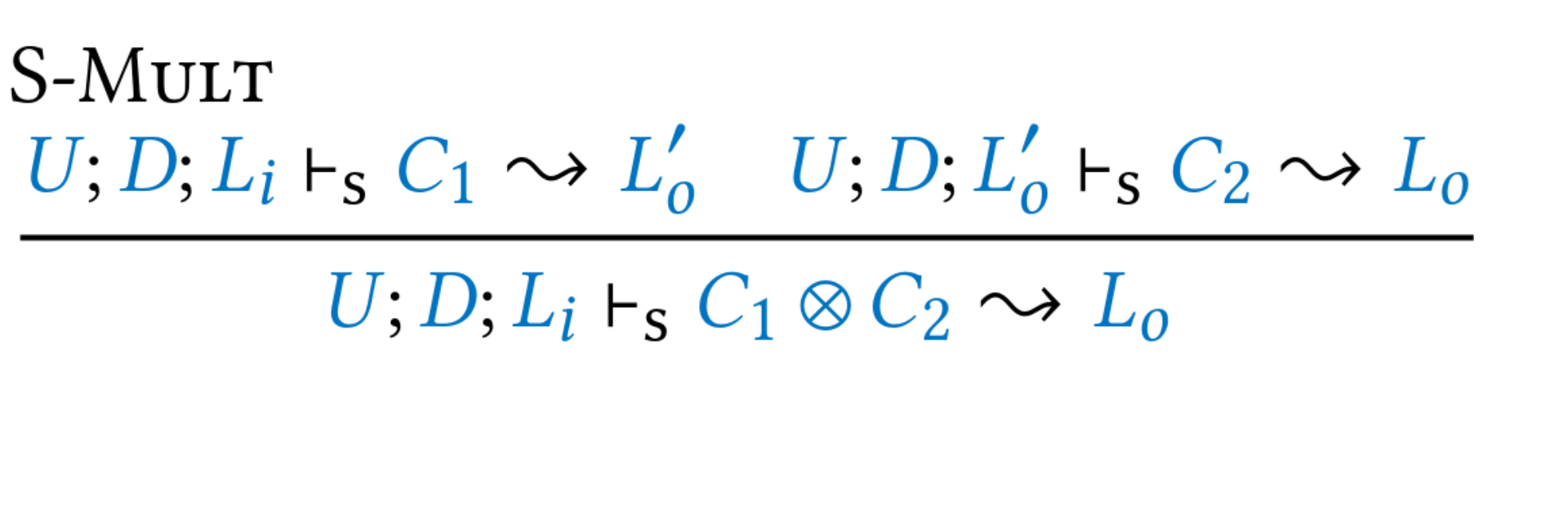
+
Declarative system
Constraint generation
Constraint solving
Inferred as
soundness
https://slides.com/aspiwack/icfp2022
https://www.tweag.io/blog/tags/linear-types/

https://dl.acm.org/doi/10.1145/3547626
