Linear constraints

Arnaud Spiwack

Joint with: Jean-Philippe Bernardy, Richard Eisenberg, Csongor Kiss, Ryan Newton, Simon Peyton Jones, Nicolas Wu

Prolific literature…

… but not much delivery

That's about it

… until GHC 9.0

GHC 9.0.1 User's Guide

Linear Haskell

 a ⊸ b

Since GHC 9.0

{-# LANGUAGE LinearTypes #-}

Completely normal Haskell + an extra type

(+ stuff for polymorphism)

(but we won't talk about it today)

Consume exactly once

f :: A ⊸ B

Linear Haskell — Jean-Philippe Bernardy, Richard Newton, Simon Peyton Jones, Arnaud Spiwack

 f u
 u

If            is consumed exactly once
then      is consumed exactly once

What does “consume exactly once” mean?

evaluate x

apply x and consume the result exactly once

decompose x and consume both components exactly once

Base type

Function

Pair

The creative step

f :: A ⊸ A ⊸ !Int ⊸ B
g :: !B ⊸ C

h :: !A ⊸ C
h (!x) = g (!(f x x (!42)))
f :: A -> A -> Int -> B
g :: B -> C

h :: A -> C
h x = g (f x x (42))

vs

Linear types seem to require deep changes to the language

(e.g. Rust)

Linear types, by examples (1/3)

id x = x

✓

linear

dup x = (x,x)

✗

not linear

swap (x,y) = (y,x)

✓

linear

forget x = ()

✗

not linear

Linear types, by examples (2/3)

f (Left x) = x
f (Right y) = y

✓

linear

✓

linear

✗

not linear

h x b = case b of
  True -> x
  False -> x
g z = case z of
  Left x -> x
  Right y -> y
k x b = case b of
  True -> x
  False -> ()

✓

linear

Linear types, by examples (3/3)

f x = dup x

✓

linear

✗

not linear

h u = u 0
g x = id (id x)
k u = u (u 0)

✓

linear

✗

not linear

Application class 1

Making more things pure

Example: safe mutable arrays

Mutable arrays: the ST way

array :: Int -> [(Int,a)] -> Array a
array size pairs = runST $ do
  fma <- newMArray size
  forM pairs (write ma)
  return (unsafeFreeze ma)
newMArray    :: Int -> ST s (MArray s a)
read         :: MArray s a -> Int -> ST s a
write        :: MArray s a -> (Int, a) -> ST s ()
unsafeFreeze :: MArray s a -> ST s (Array a)
forM         :: Monad m => [a] -> (a -> m ()) -> m ()
runST        :: (∀s. ST s a) -> a

Allocate

Fill

Freeze

 unsafeFreeze

                      is unsafe!

The same, in Linear Haskell

array :: Int -> [(Int,a)] -> Array a
array size pairs = newMArray size $ \ma ->
  freeze (foldl write ma pairs)
newMArray :: Int -> (MArray a ⊸ Ur b) ⊸ Ur b
write     :: MArray a ⊸ (Int,a) -> MArray a
read      :: MArray a ⊸ Int -> (MArray a, Ur a)
freeze    :: MArray a ⊸ Ur (Array a)
foldl     :: (a ⊸ b ⊸ a) -> a ⊸ [b] ⊸ a

Allocate

Fill

Freeze (safe!)

See Data.Array.Mutable.Linear in linear-base

Threading style

write :: MArray a ⊸ (Int,a) -> MArray a

Can't do

write ma (1, True); write ma (2, False); …

Each write returns a new array

Scope passing style

newMArray :: Int -> (MArray a ⊸ Ur b) ⊸ Ur b

This is what ensures that references to arrays are unique

Unrestricted

data Ur a where
  Ur :: a -> Ur a

compare with

data Id a where
  Id :: a ⊸ Id a

Data types are linear by default

Scope passing style (continued)

newMArray :: Int -> (MArray a ⊸ Ur b) ⊸ Ur b

Don't work:

newMArrayDirect :: Int ⊸ MArray a
newMArrayLeaky :: Int -> (MArray a ⊸ b) ⊸ b

If the result is consumed exactly once
then the argument is consumed exactly once

Remember

Application class 2

Protocols in types

Example: files

I/O protocols

Files

  • ensure you close a file
  • ensure no read after close

Malloc

  • ensure you free a block
  • ensure no read after close

Sockets

  • ensure bind a socket before reading from it
  • ensure you close it
  • ensure you don’t read or bind after close

Files

openFile  :: FilePath -> IOL Handle
readLine  :: Handle ⊸ IOL (Handle, Ur String)
closeFile :: Handle ⊸ IOL ()
firstLine :: FilePath -> IOL (Ur String)
firstLine fp = do
  h <- openFile fp
  (h, Ur xs) <- readLine h
  closeFile h
  return $ Ur xs

Monads already have scope

do { x <- u ; v} = u >>= \x -> v
(>>=) :: IOL a ⊸ (a ⊸ IOL b) ⊸ IOL b

About the type of monads see A Tale of Two Functors or: How I learned to Stop Worrying and Love Data and Control — Arnaud Spiwack

Linear constraints

Coming back to files

openFile  :: FilePath -> IOL Handle
readLine  :: Handle ⊸ IOL (Handle, Ur String)
closeFile :: Handle ⊸ IOL ()
firstLine :: FilePath -> IOL (Ur String)
firstLine fp = do
  h <- openFile fp
  (h, Ur xs) <- readLine h
  closeFile h
  return $ Ur xs

The same 🙁

(Inter)Mezzo

Programming with permissions in Mezzo — François Pottier, Jonathan Protzenko

Doesn't return a new copy of ys

Constraints

show :: Show a => a -> String

A constraint

Prolog-like language

Constrained

With paramodulation

Idea: teach constraints linear logic

Files with linear constraints

Linear Constraints — Jean-Philippe Bernardy, Richard Eisenberg, Csongor Kiss, Arnaud Spiwack, Nicolas Wu

openFile  :: FilePath -> IOL (exists h. Ur (Handle h) <=%1 Open h)
readLine  :: Open h %1=> Handle -> IOL (Ur String)
closeFile :: Open h %1=> Handle -> IOL ()
firstLine :: FilePath -> IOL (Ur String)
firstLine fp = do
  Pack! h <- openFile fp
  Pack! xs <- readLine h
  closeFile h
  return $ Ur xs

Constraint generation

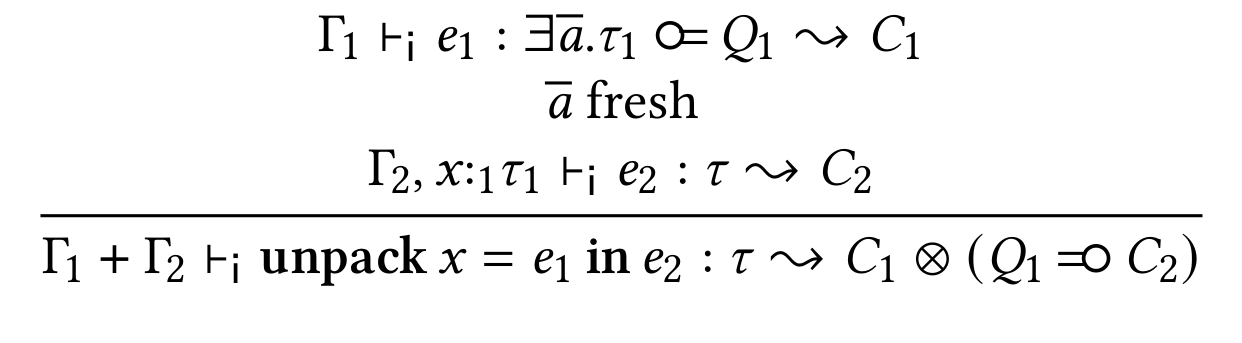
Constraints are generated (as in GHC)

in a linear logic (new!)

C₂ to be proved under linear assumption Q₁

Constraint generation (case)

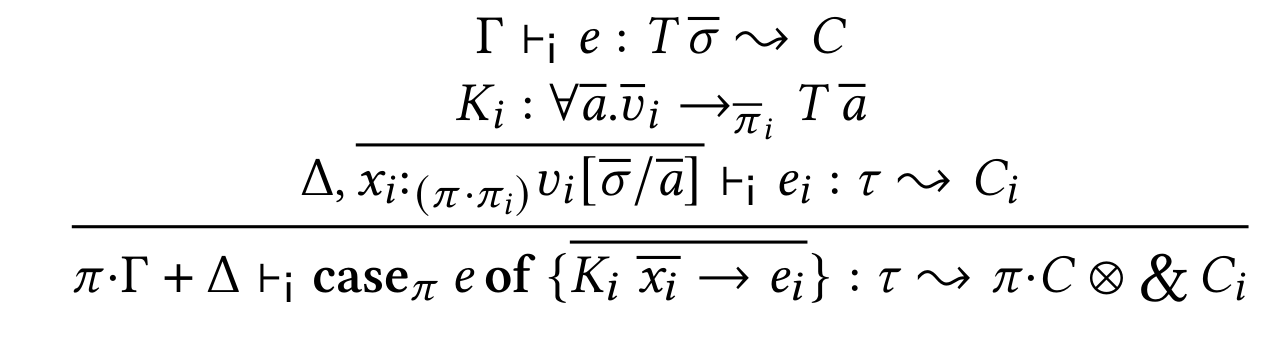
Additive conjunction

Constraint resolution

“Hereditary Harrop” fragment of Linear Logic

Logic Programming in a Fragment of Intuitionistic Linear Logic — Joshua Hodas and Dale Miller

Efficient resource management for linear logic proof search — Iliano Cervesato, Joshua Hodas, Frank Pfenning

Reduces non-determinism to one rule

↳ add a strategy (“guess free”)

Will support current extension (“quantified constraints”)

Notion: uniform proof

↳ Originally: completeness of goal-oriented search

↳ For Linear Constraints: soundness(!!) of constraint generation

https://slides.com/aspiwack/lix202103

https://www.tweag.io/blog/tags/linear-types/

\chi

https://arxiv.org/abs/2103.06127