Destination calculus

Thomas Bagrel & Arnaud Spiwack

A linear λ-calculus for purely functional memory writes

Map isn't tail recursive

let rec map f = function
  | [] -> []
  | a::l -> (f a) :: (map f l)

let mapk f l =
  let rec mapk k = function
    | [] -> k []
    | a::l -> map (fun l' -> (f a) :: l') l
  in
  mapk (fun l' -> l') l

let mapr f l =
  let rec rev acc = function
    | [] -> acc
    | a::l -> rev (a::acc) l
  and mapr acc = function
    | [] -> rev [] acc
    | a::l -> rev_map ((f a) :: acc) l
  in
  mapr [] l

😱

Solutions?

Tail recursion with one pass and mutation

type 'a mlist =
  | Nil
  | Cons of 'a * 'a mlist ref

let mapm f =
  let rec mapm (h,r) = function
    | Nil -> (r := Nil; !h)
    | Cons (a, l) -> begin
       let r' := ref Nil in
       r := (a :: r');
       mapm (h, r') !l
    end
  in
  let r := ref Nil in
  mapm (r, r)

Tail recursion modulo constructor

let[@tail_mod_cons]
  rec map f = function
  | [] -> []
  | a::l -> (f a) :: (map f l)

let mapm f =
  let rec mapm (h,r) = function
    | Nil -> (r := Nil; !h)
    | Cons (a, l) -> begin
       let r' := ref [] in
       r := (a :: r');
       mapm (h, r') !l
    end
  in
  let r := ref [] in
  mapm (r, r)

compiler
magic

Tail Modulo Cons – Frédéric Bour, Basile Clément, Gabriel Scherer

Linear one-hole contexts

let mapm f =
  let rec mapm (h,r) = function
    | Nil -> (r := Nil; !h)
    | Cons (a, l) -> begin
       let r' := ref Nil in
       r := (a :: r');
       mapm (h, r') !l
    end
  in
  let r := ref Nil in
  mapm (r, r)

interp

let mapk f l =
  let rec mapk k = function
    | [] -> k []
    | a::l -> map (fun l' -> (f a) :: l') l
  in
  mapk (fun l' -> l') l

Linear

Linear
no pattern-match

\alpha\hat{\multimap}\beta

A functional representation of data structures with a hole – Yasuhiko Minamide

The Functional Essence of Imperative Binary Search Trees – Anton Lorenzen, Daan Leijen, Wouter Swierstra, and Sam Lindley

Breadth-first traversal

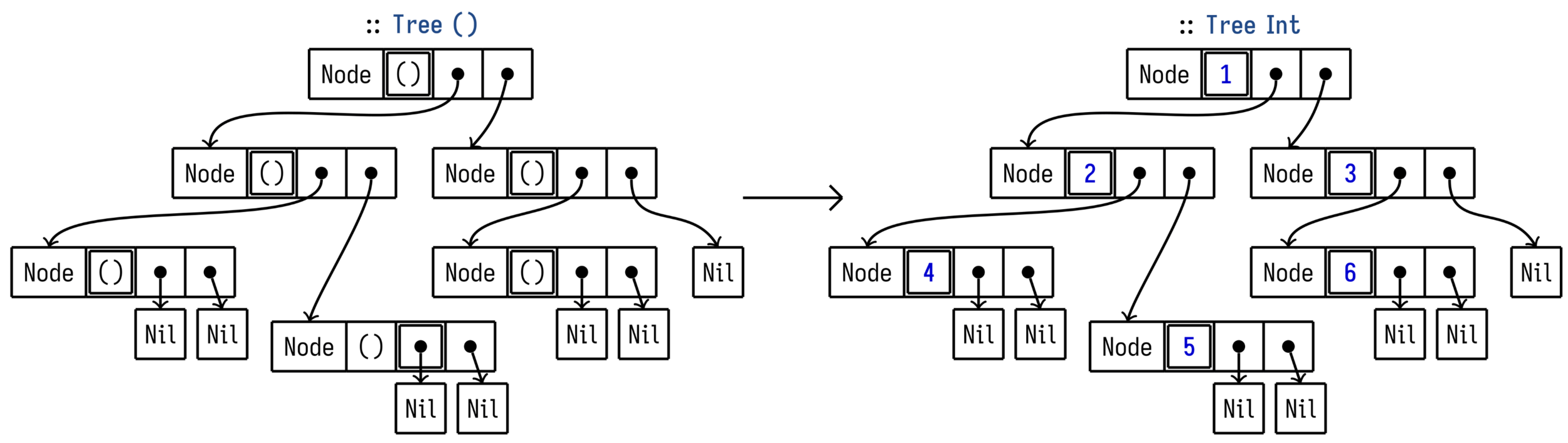
Destinations

\alpha\mathop{\hat{\multimap}}\beta

\alpha\multimap\beta

\beta\multimap\alpha^\bot

\beta\ltimes\lfloor\alpha\rfloor

= Ampar b (Dest a)

Breadth-first traversal with destinations

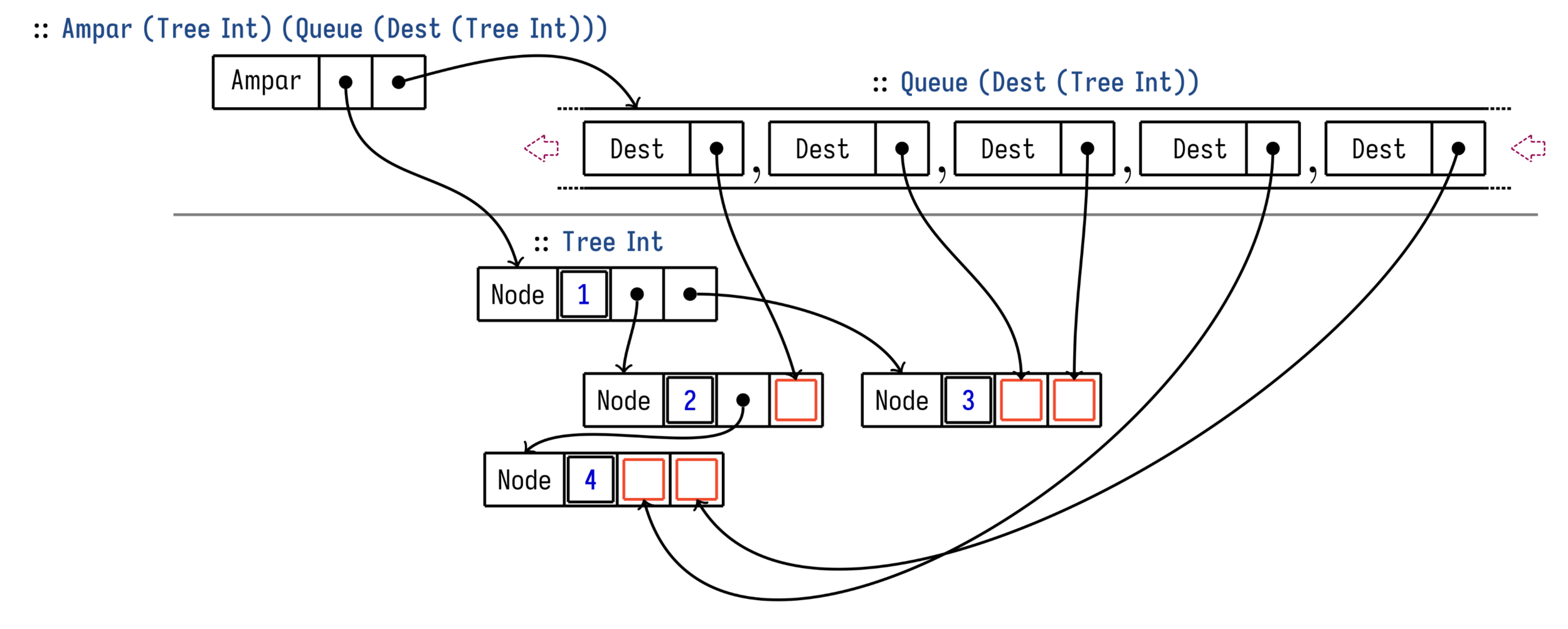
The linearity contract

\alpha\multimap\beta

When you evaluate

then you evaluate

But what if you put the argument in a Dest and make it 🪄 disappear?

A solution for the ages

https://slides.com/aspiwack/oopsla2025

https://www.tweag.io/blog/tags/linear-types/

https://dl.acm.org/doi/abs/10.1145/3720423

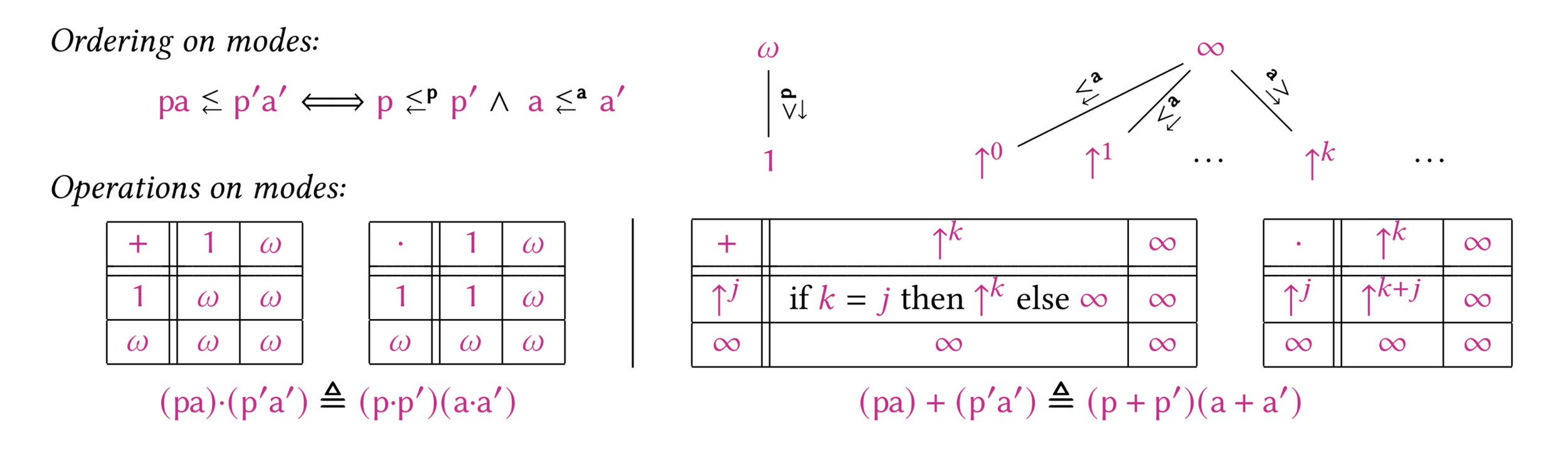
Ages are implicit in most typing rules

Only semiring operations

Ages where relevant

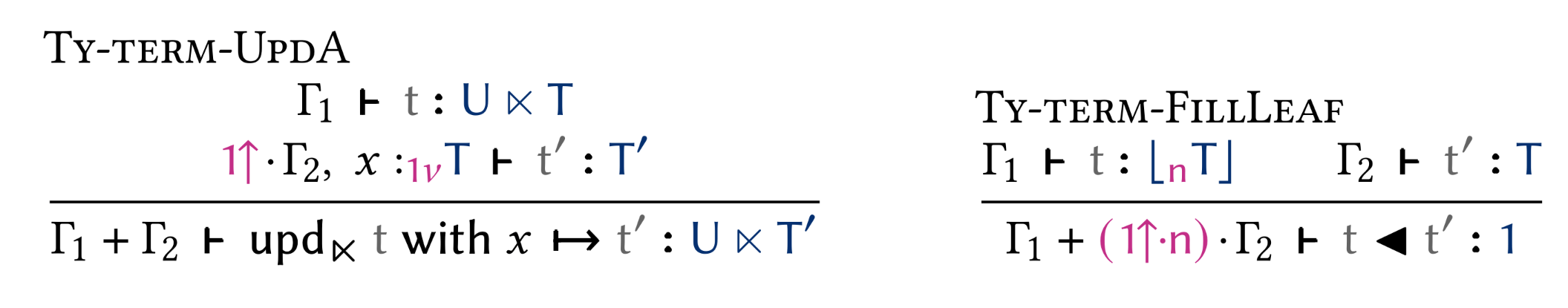
How to segfault (without ages)

let outer :: Ampar (Dest ()) ()
    outer = (newAmpar tok1) `updWith` \(dd :: Dest (Dest ())) →
              let inner :: Ampar () ()
                  inner = (newAmpar tok2) `updWith` \(d :: Dest ()) →
                            dd &fillLeaf d
               in fromAmpar' inner
 in fromAmpar' outer