NumPy - Python's missing array class
NumPy
NumPy is a fantastic package to have in your programming toolbox
Where Python falls short on performance, NumPy steps in to provide C/Fortran speeds
What is NumPy?
NumPy provides a powerful N-dimensional array class
import numpy as np
a = np.array([1,2,3,4])Fast C and Fortan speed operations
a = np.array([1,2,3])
np.sum(a)Use NumPy when you have large collections of regular data
Talk Outline
I'm going to present features of NumPy and include many examples
Then discuss integrations of NumPy with packages like SciPy, Matplotlib, and Pandas
Ask questions along the way!

np.array
Numpy's array class is powerful!
>>> import numpy as np
>>> a = np.array([-3,5,1,4])
>>> a[0]
-3
>>> a[:2] # supports slicing like lists
array([-3, 5])
>>> b = np.array([[3,2,4], [2,1,5]]) # 2x3 array
>>> b
array([[3, 2, 4],
[2, 1, 5]])
>>> b.shape
(2, 3)
Similar to a python list which is an ordered collection of data
shape explains the dimensionality
np.array : <feature>
Features of numpy's array class
np.array : dtype
NumPy arrays are typed
Typing is part of what gives NumPy it's speed
The any array generation function will accept dtype=? and you can specify a type
also an astype method which allows you to cast
>>> a = np.array([1,2,3], dtype=float)
>>> a
array([ 1., 2., 3.])
>>> a.dtype
dtype('float64')
>>> a.astype(str)
array(['1.0', '2.0', '3.0'], dtype='|S32')
>>> np.array([True, False, False])
array([ True, False, False], dtype=bool)
>>> np.array([{1:2}, {3:4}])
array([{1: 2}, {3: 4}], dtype=object)
>>> np.array(['s1', 50, 'longer_string'])
array(['s1', '50', 'longer_string'], dtype='|S13')
>>> np.array(['5', 50, '100'], dtype=int)
array([ 5, 50, 100])
>>> np.array(['5', 50, 'fail'], dtype=int)
ValueError: invalid literal for long() with base 10: 'fail'
np.array : slicing
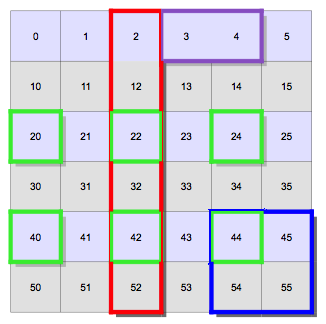
>>> a = np.array([array to the right])
>>> a[0, 3:5]
array([3, 4])
>>> a[ :, 2 ]
array([2, 12, 22, 32, 43, 52])
>>> a[4:, 4:]
array([[44, 45],
[54, 55]])
>>> a[ ::-1, 2 ] # reversed
array([52, 42, 32, 22, 12, 2])
>>> a[2::2, 2::2]
array([[22, 24],
[42, 44]])
= np.arange(0,60).reshape((6, -1))[:,:6]
np.array : element-wise operations
An operation is performed on each element of the array not the entire array
>>> a = np.array([2,3,5])
>>> a*2
array([4,6,10])
>>> a+5
array([7,8,10])
np.array : shape and reshaping
Each array has a shape
shapes can be modified to produce new arrays
>>> a = np.array([[1, 2, 3, 4],
[10, 12, 13, 14],
[20, 22, 23, 24]
])
>>> a
array([[ 1, 2, 3, 4],
[10, 12, 13, 14],
[20, 22, 23, 24]])
>>> a.shape
(3, 4)
>>> a.size
12
>>> a.reshape((4,3))
array([[ 1, 2, 3],
[ 4, 10, 12],
[13, 14, 20],
[22, 23, 24]])
>>> a.reshape(2, -1)
array([[ 1, 2, 3, 4, 10, 12],
[13, 14, 20, 22, 23, 24]])
>>> a.ravel()
array([ 1, 2, 3, 4, 10, 12,
13, 14, 20, 22, 23, 24])
np.array : Transpose
For a multidimensional array you can transpose the elements (e.g. (i,j) to (j,i))
>>> a = np.array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
>>> a.T
array([[ 0, 5, 10, 15],
[ 1, 6, 11, 16],
[ 2, 7, 12, 17],
[ 3, 8, 13, 18],
[ 4, 9, 14, 19]])
Array Generation
- arange -- much like python's range
- linspace -- break up range into number of elements
- ones, zeros -- creates an array of ones or zeros
- repeat -- an element that number of times
- empty -- empty array
- ?_like -- a few like zeros_like which create from another
>>> np.arange(0, 6, 1.5) # 1
array([ 0. , 1.5, 3. , 4.5])
>>> np.linspace(0, 6, 4) # 2
array([ 0., 2., 4., 6.])
>>> np.ones(5) # 3
array([ 1., 1., 1., 1., 1.])
>>> np.zeros((3,3)) # 3 with shape
array([[ 0., 0., 0.],
[ 0., 0., 0.],
[ 0., 0., 0.]])
>>> np.repeat(3.14, 3) # 4
array([ 3.14, 3.14, 3.14])
>>> np.empty((2,2)) # 5
array([[ 0., 0.],
[ 0., 0.]])
>>> np.zeros_like(np.arange(5)) # 6
array([0, 0, 0, 0, 0])
Fancy Indexing
In addition to slicing you can do fancy indexing
This includes using a list of indices or an boolean array
These create views of the data which can be assigned to
>>> a = np.array([2, 4, 6, 8, 10, 12, 14])
>>> a[[0,3,5]]
array([2, 8, 12])
>>> idx = [0, 3, 5]
>>> a[idx]
array([2, 8, 12])
>>> mask = np.array([True, False, False, True, True, False, True])
>>> a[mask]
array([2, 8, 10, 14])
>>> a[mask] = 0
array([0, 4, 6, 0, 0, 12, 0]) Masking
Can create masks of the data based on logic
supports logic operations with &(and), |(or), ~(not)
np.logical_xor
>>> a = np.arange(0,20).reshape(5, 4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
>>> mask_1 = a > 10
>>> mask_1
array([[False, False, False, False],
[False, True, True, True],
[ True, True, True, True]], dtype=bool)
>>> mask_2 = a <= 18
>>> mask_2
array([[ True, True, True, True],
[ True, True, True, True],
[False, False, False, False]], dtype=bool)
>>> mask_1 & mask_2
array([[False, False, False, False],
[False, True, True, True],
[False, False, False, False]], dtype=bool)
>>> a[mask_1 & mask_2]
array([12, 13, 14])Masking
Use masking to create fast subsets of data
>>> data = {}
>>> data['heights'] = np.array([75., 70., 63.5, 67., 79., 64., 73.]) # inches
>>> data['gender'] = np.array(['m', 'f', 'm', 'm', 'f', 'f', 'm'])
>>> mask = data['heights'] < 72.0
>>> data['gender'][mask]
array(['f', 'm', 'm', 'f'])
pro-tip: create all your masks first then apply them
Mask Checks
- any -- are any True?
- all -- are all True?
- where -- return index of where is True.
>>> a = np.array([0, 1, 1, 0, 0, 1], dtype=bool)
>>> a
array([False, True, True, False, False, True], dtype=bool)
>>> np.all(a)
False
>>> np.any(a)
True
>>> np.where(a)
(array([1, 2, 5],)
Broadcasting
Broadcasting is a concept with rules which allows functions to combine arrays of different shapes
Technically this is how the element wise operations perform
(e.g. a + 1)
>>> a = np.arange(20).reshape(10, -1)
>>> a
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7],
[ 8, 9],
[10, 11],
[12, 13],
[14, 15],
[16, 17],
[18, 19]])
>>> b = np.array([1, 1])
>>> a+b
array([[ 1, 2],
[ 3, 4],
[ 5, 6],
[ 7, 8],
[ 9, 10],
[11, 12],
[13, 14],
[15, 16],
[17, 18],
[19, 20]])
>>> a.shape
(10, 2)
>>> b.shape
(2,)
Combining Arrays
Several utilities exist for combining arrays together
You will most likely need to be aware of the array shapes
>>> a = np.array([[1,2],[3,4]])
>>> b = np.array([[4,5],[6,7]])
>>> np.hstack((a,b))
array([[1, 2, 4, 5],
[3, 4, 6, 7]])
>>> np.vstack((a, b))
array([[1, 2],
[3, 4],
[4, 5],
[6, 7]])
>>> np.dstack((a, b))
array([[[1, 4],
[2, 5]],
[[3, 6],
[4, 7]]])
>>> np.concatenate((a.ravel(),b.ravel())
array([1, 2, 3, 4, 4, 5, 6, 7])
>>> np.concatenate((a.ravel(), b))
ValueError: all the input arrays must
have same number of dimensions
Functions : never import math again
Numpy has math functions
sin, cos, tan, sum, power, sqrt, etc.
Can use the numpy function on numbers
>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> np.sqrt(a)
array([ 0., 1., 1.41421356, 1.73205081, 2.])
>>> np.arctan(a)
array([ 0., 0.7853, 1.10714, 1.2490, 1.3258])
>>> a[3] = 20
>>> np.max(a)
20
>>> a[1] = np.nan
>>> np.max(a)
np.nan
>>> np.nanmax(a)
20
>>> np.sqrt(4)
2
Functions : Basic stats
Numpy supports some basic statistics including mean, standard deviation, convolution
even do polynomial fitting
>>> a = np.array([3,-1,4,0,3,20]
>>> np.mean(a)
4.8333
>>> np.std(a)
7.0099
>>> x = np.arange(-10, 10, 0.6)
>>> y = np.random.normal(0, 3, len(x))
>>> coefficients = np.polyfit(x, y, 3)
>>> np.polyval(coefficients, np.arange(10, 15, 0.3))
>>> x2 = np.arange(-10, 10, 3)
>>> y2 = np.interp(x2, x, y)
Functions : Ordering
Numpy has math functions
sin, cos, tan, sum, power, sqrt, etc.
Can use the numpy function on numbers
>>> a = np.array([3,-1,4,0,3,20]
>>> np.argsort(a)
array([1, 3, 0, 4, 2, 5])
>>> idx = np.argsort(a)
>>> a[idx]
array([-1, 0, 3, 3, 4, 20])
>>> np.sort(a)
array([-1, 0, 3, 3, 4, 20])
>>> a.sort()
>>> a
array([-1, 0, 3, 3, 4, 20])Functions : random number generation
Numpy has a module for random numbers
>>> np.random.random(5)
array([ 0.3577, 0.8275, 0.94499, 0.768, 0.2198])
>>> np.random.normal(0, 1, 10)
array([ 0.142 , -0.1082, -0.5035, 0.0059,
0.0165, -0.4864, 0.5475,
0.269 , -0.9024, 0.3165])
>>> np.random.uniform(0, 5, 10)
array([ 0.5204, 4.051 , 0.1581, 4.9441,
1.8538, 3.1539, 1.7153,
0.7021, 1.6248, 2.4531])Functions : reading and writing
Functions which will output as a text file
genfromtxt will read in csv data
>>> a = np.random.random(5)
>>> np.savetxt('data.txt', a)
>>> a = np.genfromtxt('data.txt')Integration
Pandas - Good if you have 2-dim data want to index by something other than integers
Scipy - Has many more statistics and model fitting which is all built on numpy
Matplotlib - Good for visualizing arrays
Discuss
Thanks!
gregersen.dylan@gmail.com
astrodsg.github.io