生活中的Computer science
Lesson 5: 不過就是排序,有什麼難的?
演算法概論
演算法是什麼?
解決問題的方法
輸入 -> 方法 -> 輸出
問題:給一個數字,問說是不是質數
輸入:37
演算法:把每個小於它的數拿來除,看能否整除
輸出:Yes
問題:給一個數字,求排列組合
輸入:123
演算法:把數字的位置調換,直到出現所有組合
輸出:123, 132, 213, 231, 312, 321
演算法只是解決問題的方法
你不一定要懂程式
(但懂了會比較聽得懂)
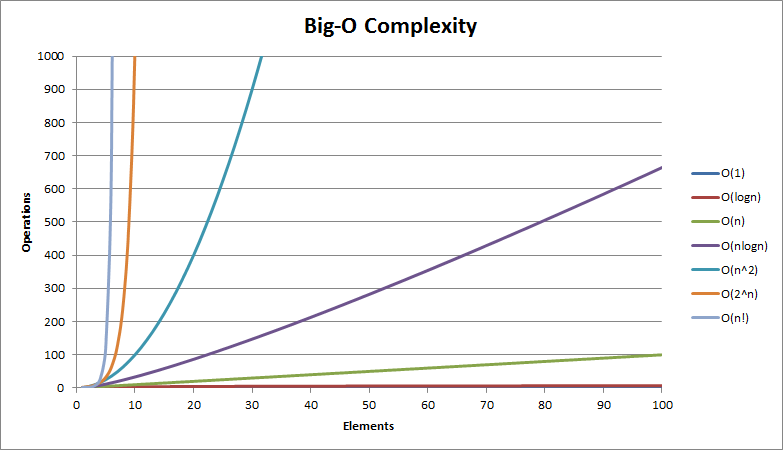
怎麼評估演算法的好壞?
時間複雜度
平均狀態下,一個演算法需要多少時間來完成
搜尋
你有一個數列,當中有n個數字
一共有m次查詢,問你這個數字是否存在
n = 10
數列: 10, 1, 93, 12, 94, 11, 102, 4, 2, 38
怎麼查?
阿不就每次都從第一筆看到最後一筆嗎
時間複雜度:O(nm)
如果n跟m差不多的話,可以看作是O(n^2)
每次要找數字,都一定要從第一個查到最後一個
有沒有更好的做法?
如果我們的數列是排序過的,會發生什麼事?
10, 1, 93, 12, 94, 11, 102, 4, 2, 38
排序過後: 1, 2, 4, 10, 11, 12, 38, 93, 94, 102
利用排序過後的特性(後面一定大於前面)
可以做些什麼事情?
大家有玩過終極密碼嗎
關主先指定一個數字跟範圍
例如說1~100,答題者不斷猜數字,猜中就贏了
最快的方法是什麼?
終極密碼(假設答案是1)
- 第一次猜50,範圍變1~49
- 第二次猜25,範圍變1~24
- 第三次猜12,範圍變1~11
- 第四次猜6,範圍變1~5
- 第五次猜3,範圍變1~2
- 第六次猜2,範圍變1~1
- 第七次猜1,猜中
終極密碼(假設答案是27)
- 第一次猜50,範圍變1~49
- 第二次猜25,範圍變26~49
- 第三次猜37,範圍變26~36
- 第四次猜31,範圍變26~31
- 第五次猜28,範圍變26~27
- 第六次猜26,範圍變27~27
- 第七次猜27,猜中
假設現在有2個數字,猜2次一定可以猜中
假設現在有4個數字,猜3次一定可以猜中
假設現在有8個數字,猜4次一定可以猜中
1 2 3 4 5 6 7 8,如果我猜4,答案有三種
第一種是答案就是4,那就中了
第二種是範圍變成剩1, 2, 3可以猜
第三種是範圍變成剩5, 6, 7, 8可以猜
依據上面所推出的,4個數字猜3次一定可以猜中
以此類推,16個數字,猜5次一定中
32個數字,猜6次,64個猜七次,128個猜八次
所以100個數字,猜7次一定可以猜中
回到我們剛才的搜尋
1, 2, 4, 10, 11, 12, 38, 93, 94, 102
一共十個數字
假設現在要找3有沒有在裡面
先找最中間的數字,12,發現3<12
所以如果3在數列裡,範圍一定是12的左邊
1, 2, 4, 10, 11, 12, 38, 93, 94, 102
再找範圍內最中間的數字,4,發現3<4
所以如果3在數列裡,範圍一定是4的左邊,
1, 2, 4, 10, 11, 12, 38, 93, 94, 102
再找範圍內最中間的數字,2,發現2>3
所以如果3在數列裡
範圍一定是2的右邊,4的左邊
發現範圍裡面沒數字了,所以找不到
1, 2, 4, 10, 11, 12, 38, 93, 94, 102
二分搜尋法
Binary Search
藉由排序過後的特性,一直從中間切切切切切
就不必從頭到尾找數字,而是能更有方法、效率地去找
時間複雜度從原本的O(n^2)變成
選擇排序法
Selection Sort
從還沒排序的數列裡面找到最小的,然後移到最左邊
泡沫排序法
Bubble Sort
由左到右兩兩比較,把比較大的數字往右邊移
也因為這樣,可以想成是比較大的數字會「浮上來」
因此取名叫做泡沫排序法
插入排序法
Insertion Sort
其實就是你玩撲克牌的時候,會用到的排序法
從左邊開始,把每一張牌都插入到應該在的位置
合併排序法
Merge Sort
有一種方法叫做Divide and Conquer
把大問題分割成小問題,把小問題解決以後,大問題也解決了
假設你現在有個數列是1, 4, 3, 7, 9, 2, 5, 8
分割成兩半,1, 4, 3, 7跟9, 2, 5, 8
個別做好排序以後,就是1, 3, 4, 7跟2, 5, 8, 9
那現在要怎麼把兩個排序好的數列變成一個?
很簡單,你先看兩邊最左邊的數字,發現1比較小
於是就放1,再來看左邊第二個跟右邊第一個,取2
接著左二(3)跟右二(5),取左二
再來左三(4)跟右二(5),取左三
再來左四(7)跟右二(5),取右二
以此類推
最後就可以組合出一個排序好的數列
快速排序法
Quick Sort
顧名思義,就是很快的排序法
挑選一個基準點(pivot)
保證左邊的數字都小於它,右邊的數字都大於它
然後對左右兩邊重複此項操作
特殊的排序法
100萬個數字
數字範圍都在1~100以內
如何排序?
計數排序
Count Sort
因為數字的範圍遠比數字數量小太多了
所以我們可以用計數的方法
算算個1有幾個, 2有幾個...100有幾個
就可以達成排序的效果了