Building a Rendering Engine in Tensorflow
Twitter: @awildtaber, Github: ataber
Full blog post on Medium, username @awildtaber
Geometric Representations
- Polygonal (Meshes)
- Parametric (Boundary Representation)
- Implicit (Function Representation)
Parametric Representation
Represent geometry as the image of a function
Easy to get local data
Just walk in the u or v direction
Hard to query point membership
Requires solving a hard computational geometry problem every time
Hard to perform boolean operations
Modeling complex shapes requires many parametric patches
Which means exploding memory cost for things like microstructures

Implicit Representation
Represent geometry as the kernel of a function
Easy to perform boolean operations
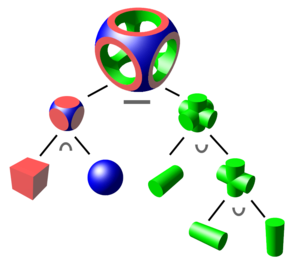
Can model essentially arbitrary complexity with low storage overhead

Rendering is time-consuming
You trade space for time
User interaction is not intuitive
Everything is inherently global
Signed Distance Functions
Special case of implicit representations
The magnitude of the function underestimates the distance to the nearest surface
Underestimation is important because there are some surfaces (looking at you, ellipse) which do not have closed-form distance functions
When (x,y,z) is inside (outside) the surface, the function's sign is positive (negative)
Prior Art
An Example
from math import sqrt
def cylinder(radius):
def equation(x, y, z):
return radius - sqrt(x**2 + y**2)
return equation
my_cylinder = cylinder(1)
assert(my_cylinder(0, 0, 0) == 1) # 1 unit inside cylinder
assert(my_cylinder(1, 0, 0) == 0) # on wall
assert(my_cylinder(2, 0, 0) == -1) # 1 unit outside cylinderAn Example
def intersection(f, g):
def intersected(x, y, z):
return min(f(x, y, z), g(x, y, z))
return intersected
def plane(normal, offset):
def equation(x, y, z):
a, b, c = normal
return x*a + y*b + z*c + offset
return equation
my_plane = plane([0, 0, 1], 0) # as in: this is myPlane get theseSnakes off it!
my_cylinder = cylinder(1)
cut_cylinder = intersection(my_cylinder, my_plane)
assert(cut_cylinder(0, 0, -2) == my_plane(0, 0, -2)) # like a plane below z = 0
assert(cut_cylinder(0, 1, 2) == my_cylinder(0, 1, 2)) # like a cylinder above z = 0Build Geometry with Closures
Combine primitives lazily
Build a syntax tree in the language of geometries and operations
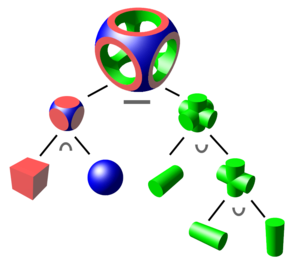
Rendering Signed Distance Functions
Solving a bunch of equations
Polygonization
Populate a grid with values of the function and use that grid to approximate the surface with triangles
Raytracing
Setup a camera in space, and for each pixel, send a ray to intersect the surface. Draw the intersected points to the screen
Polygonization
Marching Cubes

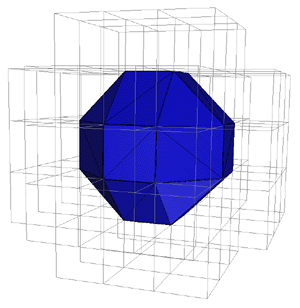
Raytracing
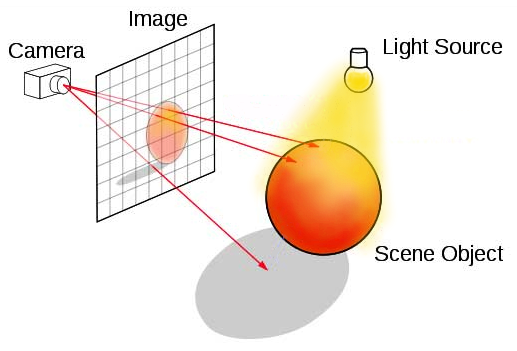

How can Tensorflow help?
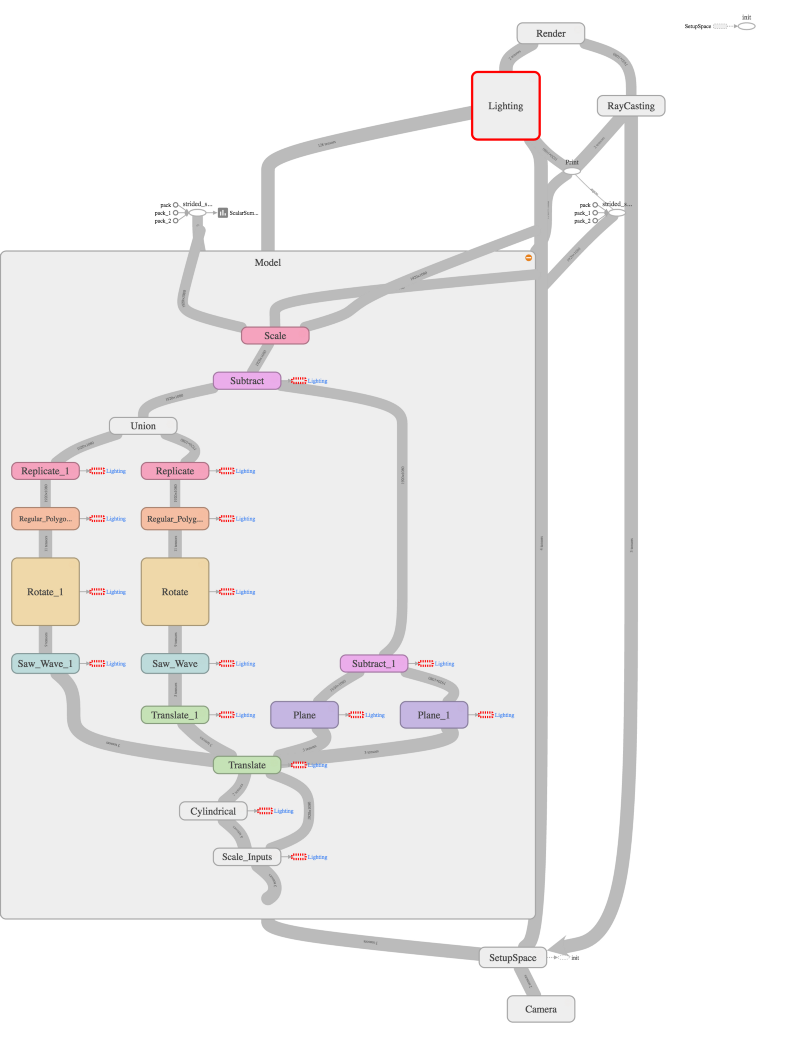
Our representations are trees, and therefore graphs
We would like to:
- Reuse computation results automatically
- Perform efficient computations on large tensors
- Parallelize!
Tensorflow comes with:
- Common subexpression elimination
- Automatic differentiation
- Compilation to GPU code
Easy to implement*
import tensorflow as tf
cylinder_tf = my_cylinder(tf.constant(0.0), tf.constant(1.0), tf.constant(2.0))
session = tf.Session()
cylinder_tf_result = session.run(cylinder_tf)
assert(cylinder_tf_result == my_cylinder(0, 1, 2))*Some Tensorflow-specific functions are needed like tf.maximum instead of max
Works with tf.Variable and tf.Placeholder too!
Polygonizing SDFs in Tensorflow
Input a tensor for each coordinate
min_bounds = [-1,-1,-1] # the geometric coordinate bounds
max_bounds = [1,1,1]
output_shape = [200,200,200]
resolutions = list(map(lambda x: x*1j, output_shape))
mi0, mi1, mi2 = min_bounds
ma0, ma1, ma2 = max_bounds
r0, r1, r2 = resolutions
space_grid = np.mgrid[mi0:ma0:r0,mi1:ma1:r1,mi2:ma2:r2]
space_grid = space_grid.astype(np.float32)
x = tf.Variable(space_grid[0,:,:,:], trainable=False, name="X-Coordinates")
y = tf.Variable(space_grid[1,:,:,:], trainable=False, name="Y-Coordinates")
z = tf.Variable(space_grid[2,:,:,:], trainable=False, name="Z-Coordinates")
draw_op = function(x,y,z)
session = tf.Session()
session.run(tf.initialize_all_variables())
volumetric_grid = tf.session.run(draw_op)
marching_cubes(volumetric_grid) # => list of faces and vertices for renderingTensorboard!
Raytracing SDFs in Tensorflow
Solve the equations for t:
First build image plane
def vector_fill(shape, vector):
return tf.pack([
tf.fill(shape, vector[0]),
tf.fill(shape, vector[1]),
tf.fill(shape, vector[2]),
])
resolution = (1920, 1080)
aspect_ratio = resolution[0]/resolution[1]
min_bounds, max_bounds = (-aspect_ratio, -1), (aspect_ratio, 1)
resolutions = list(map(lambda x: x*1j, resolution))
image_plane_coords = np.mgrid[min_bounds[0]:max_bounds[0]:resolutions[0],min_bounds[1]:max_bounds[1]:resolutions[1]]
# Find the center of the image plane
camera_position = tf.constant([-2, 0, 0])
lookAt = (0, 0, 0)
camera = camera_position - np.array(lookAt)
camera_direction = normalize_vector(camera)
focal_length = 1
eye = camera + focal_length * camera_direction
# Coerce into correct shape
image_plane_center = vector_fill(resolution, camera_position)
# Convert u,v parameters to x,y,z coordinates for the image plane
v_unit = [0, 0, -1]
u_unit = tf.cross(camera_direction, v_unit)
uc, vc = image_plane_coords
center = image_plane_center
image_plane = center + uc * vector_fill(resolution, u_unit) + vc * vector_fill(resolution, v_unit)First build image plane
def vector_fill(shape, vector):
return tf.pack([
tf.fill(shape, vector[0]),
tf.fill(shape, vector[1]),
tf.fill(shape, vector[2]),
])
resolution = (1920, 1080)
aspect_ratio = resolution[0]/resolution[1]
min_bounds, max_bounds = (-aspect_ratio, -1), (aspect_ratio, 1)
resolutions = list(map(lambda x: x*1j, resolution))
image_plane_coords = np.mgrid[min_bounds[0]:max_bounds[0]:resolutions[0],min_bounds[1]:max_bounds[1]:resolutions[1]]
# Find the center of the image plane
camera_position = tf.constant([-2, 0, 0])
lookAt = (0, 0, 0)
camera = camera_position - np.array(lookAt)
camera_direction = normalize_vector(camera)
focal_length = 1
eye = camera + focal_length * camera_direction
# Coerce into correct shape
image_plane_center = vector_fill(resolution, camera_position)
# Convert u,v parameters to x,y,z coordinates for the image plane
v_unit = [0, 0, -1]
u_unit = tf.cross(camera_direction, v_unit)
uc, vc = image_plane_coords
center = image_plane_center
image_plane = center + uc * vector_fill(resolution, u_unit) + vc * vector_fill(resolution, v_unit)
Then build rays
# Populate the image plane with initial unit ray vectors
initial_vectors = image_plane - vector_fill(resolution, eye)
ray_vectors = normalize_vector(initial_vectors)
t = tf.Variable(tf.zeros_initializer(resolution, dtype=tf.float32), name="ScalingFactor")
space = (ray_vectors * t) + image_plane
# Name TF ops for better graph visualization
x = tf.squeeze(tf.slice(space, [0,0,0], [1,-1,-1]), squeeze_dims=[0], name="X-Coordinates")
y = tf.squeeze(tf.slice(space, [1,0,0], [1,-1,-1]), squeeze_dims=[0], name="Y-Coordinates")
z = tf.squeeze(tf.slice(space, [2,0,0], [1,-1,-1]), squeeze_dims=[0], name="Z-Coordinates")
evaluated_function = function(x,y,z)
Then build rays
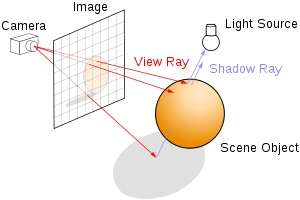
The iteration operation
Made exquisitely simple because we're using SDF's!
epsilon = 0.0001
distance = tf.abs(evaluated_function)
distance_step = t - (tf.sign(evaluated_function) * tf.maximum(distance, epsilon))
ray_step = t.assign(distance_step)Just run ray_step as many times as necessary to get convergence
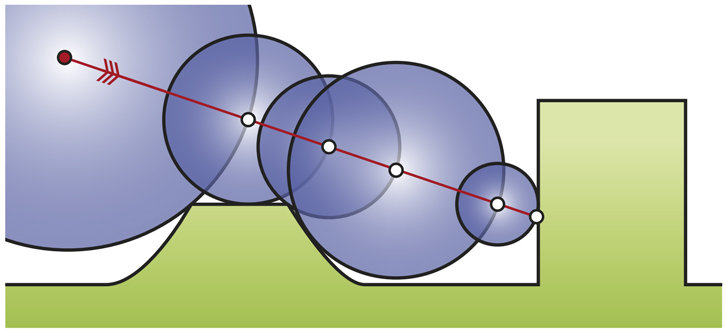
Use automatic differentiation to calculate surface normals for shading
Since the function's value increases as you get closer to the surface, it's derivative always points inward.
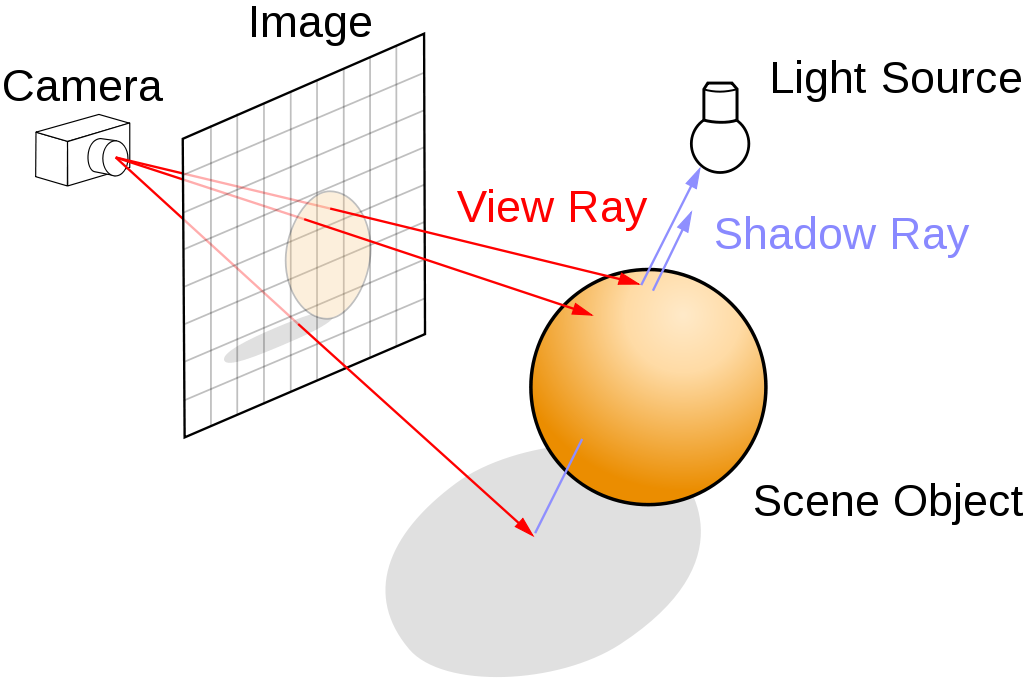
Code elided, but here's pictures!
Convert to image
# Mask out pixels not on the surface
epsilon = 0.0001
bitmask = tf.less_equal(distance, epsilon)
masked = color_modulated_by_light * tf.to_float(bitmask)
sky_color = [70, 130, 180]
background = vector_fill(resolution, sky_color) * tf.to_float(tf.logical_not(bitmask))
image_data = tf.cast(masked + background, tf.uint8)
image = tf.transpose(image_data)
render = tf.image.encode_jpeg(image)Running the iteration
session = tf.Session()
session.run(tf.initialize_all_variables())
step = 0
while step < 50:
session.run(ray_step)
step += 1
session.run(render) # <= returns jpeg data you can write to diskResult in GIF form
Each frame a parameter in the model changes
Tensorboard!
Why is this interesting?
Topology Optimization

Use tf.Variables in creating the representation and use optimization routines to increase strength to weight ratio
If you want to train on synthetic images, consider rendering them in Tensorflow
That way you have the image data in a tensor and you can calculate per-pixel gradients
Tensorflow is a powerful, generic graph computation framework
With a day job as a neural network library
Thank you!
Full blog post on Medium, username @awildtaber
Twitter: @awildtaber, github: ataber
Many thanks to Íñigo Quilez, Matt Keeter, and the Hyperfun project for inspiration/ideas