遞迴 Recursion
Laurice
遞迴是什麼?
在計算機科學中是指一種通過重複將問題分解為同類的子問題而解決問題的方法

遞迴是什麼?
在計算機科學中是指一種通過重複將問題分解為同類的子問題而解決問題的方法


遞迴是什麼?費氏數列
0, 1, 1, 2, 3, 5, 8, 13, 21.....
定義好第一項及第二項後,接下去的都是前兩項和
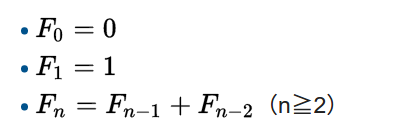
重複的工作:把前兩個數加起來
遞迴是什麼---以程式的角度來看
int my_recursion(int a){
return my_recursion(a*a);
}
int main(){
my_recursion(100);
return 0;
}簡單來說,就是函數自己呼叫自己
可是為什麼可以這樣?因為每次做的事情都一樣!!
這個程式在做什麼?
不斷的回傳my_recursion(a*a)
所以他什麼時候會停....
遞迴是什麼---以程式的角度來看
#include<iostream>
int my_recursion(int a){
//std::cout << a << '\n';
if(a > 1000)
return a * a;
return my_recursion(a * a);
}
int main(){
my_recursion(10);
return 0;
}必備元素
中止條件
遞迴條件
中止條件定義了我們在什麼情況下要停止遞迴,直接回傳值
遞迴是什麼---以程式的角度來看
小練習
我想知道一個數要用2除幾次才會小於1,可以用遞迴告訴我答案嗎?
int divide_by_two_count(double a){
//中止條件 if ..... return .....
a = a / 2;
// 我到底應該回傳什麼東西給上一層呢?
return //??????
}
int main(){
int count = divide_by_two_count(40);
return 0;
}遞迴應用
1. 費波那契數列
2. 巴斯卡三角形
3. 最大公因數
費氏數列
怎麼用遞迴算出費氏數列的第n項?
1. 先想中止條件
2. 再想我到底要遞迴什麼?
//我想知道第n項是什麼
int fibonacci(int n){
//中止條件
//if n == ..... return ....
//遞迴條件
//return fibonacci(?) + fibonacci(?)
}
int main(){
int fibo_n = fibonacci(6);
return 0;
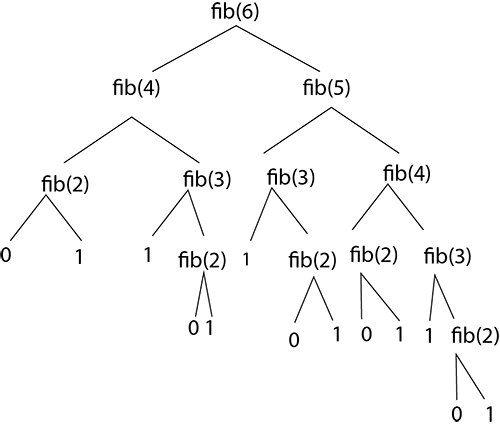
}費氏數列
怎麼用遞迴算出費氏數列的第n項?
1. 先想中止條件
2. 再想我到底要遞迴什麼?
//我想知道第n項是什麼
int fibonacci(int n){
//中止條件
if(n==0)
return 0;
if(n==1)
return 1;
//遞迴條件
return fibonacci(n-1) + fibonacci(n-2)
}
int main(){
int fibo_n = fibonacci(6);
return 0;
}
巴斯卡三角形
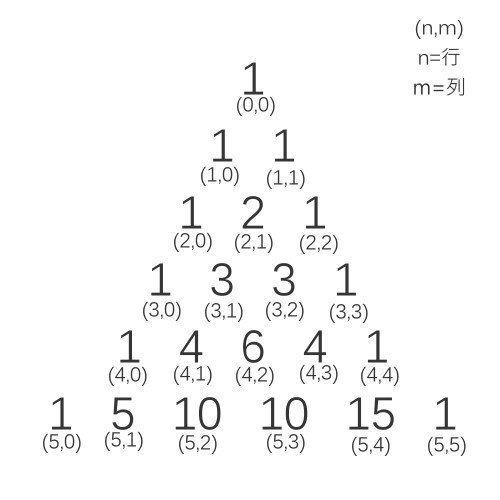
怎麼用遞迴算出三角形上的(n, m)?
1. 先想中止條件
(中止條件可以不只一個喔)
2. 再想我到底要遞迴什麼?
巴斯卡三角形

思路:
1. 哪裡要停?三角形尖端!!
2. 哪裡跟別人不一樣?邊界
3. 遞迴什麼?左上+上方就是自己
各組派人來填code吧嘿嘿嘿
巴斯卡三角形
#include<iostream>
using namespace std;
int recurrsion(int x, int y){
if(x == y) return 1;
else if (y == 0) return 1;
else{
return(recurrsion(x-1, y) + recurrsion(x-1, y-1));
}
}
int main(){
cout << recurrsion(5, 3) << endl;
return 0;
}
最大公因數 Greatest Common Divisor
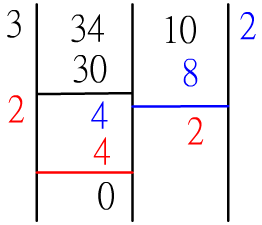
已知 a > b
根據輾轉相除法我們知道
1. 如果a被b整除
GCD(a, b) = b
2. 如果a不被b整除 GCD(a, b) = GCD(b, a%b)
最大公因數 Greatest Common Divisor
已知 a > b
根據輾轉相除法我們知道
1. 如果a被b整除 GCD(a, b) = b
2. 如果a不被b整除 GCD(a, b) = GCD(b, a%b)
int gcd(a, b){
int k = a % b;
if(k == 0)
return(b); //終止條件:b整除a
return gcd(b, k); //遞迴條件 gcd(a, b) = gcd(b, a%b)
}遞迴的效率與總結
遞迴效率
先試試看求費氏數列第100項!!
遞迴效率

每層遞迴計算很多重複的,我們可以把算過的存起來,沒算過的再算就好啦
遞迴效率
int fibonacci(int n, int fib[]) {
if(n == 0) return 0; //終止條件
if(n == 1) return 1; //終止條件
if(fib[n] == 0) //沒算過才遞迴算
fib[n] = fibonacci(n‐1, fib) + fibonacci(n‐2, fib);
return fib[n];
}
int main() {
int fib[10000] = {0}; //記得初始化
std::cout << fibonacci(100, fib);
}不過這個跑出來的答案有問題QQ 為什麼呢?
總結
1. 遞迴函數就是在函數的定義裏面呼叫自己的函數。
2. 遞迴函數至少需要包含終止條件與遞迴條件兩個部份。
3. 遞迴可以讓程式與數學定義相契合,程式碼較為簡潔易懂。
4. 遞迴可能會重複計算相同的東西多次,造成效能的浪費。
5. 將結果儲存下來可以減少計算量,提升效能。
6. 遞迴太多層電腦可能會死給你看~