Advertising Coq
Proofs ≈ Programs

Hindsight is 2020
What I believed
about Proofs:
- Magic Incantations
- Memorize and recite
- Nothing to do with programming
What I now know
about Proofs:
- Formally verifiable
- It is a skill
- It is programming
Coq is for
- Mathematicians
- Computer Scientists
- Gamers
Coq is for Mathematicians
- Reasoning Tool
- Explore new areas
- Keep track
- Automatically Check Proofs
- Avoid Mistakes
- Do not have to convince anyone
Trust the Computer

"I now do my mathematics with a proof assistant" - Vladimir Voevodsky (Fields Medal Winner)
Reasoning Tool
"The areas I found of value and of beauty, I didn't have tools to explore" - Vladimir Voevodsky
Proofs aided by Coq
- Four Colour Theorem
- Kepler conjecture
- Feit-Thompson theorem on finite groups
- Fundamental theorem of Algebra
- Wave Equation Resolution Scheme
Coq is for Computer Scientists
- Reasoning Tool
- Programming Language Design
- Optimization
-
Better Sleep
- Security
- Hardware
Unit Testing
assert (reverse [1,2]) [2,1]
assert (reverse []) []
assert (reverse [1,2,1]) [1,2,1]Property Based Testing
import Test.QuickCheck
property_double_reverse :: [Int] -> Bool
property_double_reverse xs =
reverse (reverse xs) == xs
main = quickCheck property_double_reverseVerification with Proofs
Theorem double_reverse:
forall {A: Type} (xs: list A),
reverse (reverse xs) = xs.
Proof.
...Proofs for Programs
Coq is for Gamers

Geekiest Computer Game
deMorgen Demo
Theorem deMorgen:
forall x y: bool,
not (x || y) = (not x) && (not y).Induction Demo
Inductive nat: Set :=
| O : nat (* zero *)
| S : nat -> nat (* 1 + nat *)
.
(* 3 = S (S (S O))) *)
Fixpoint sum_to_n (n: nat): nat :=
match n with
| O => O
| (S n') => n + sum_to_n n'
end.
(* sum_to_n 3 = 3 + 2 + 1 + 0 *)Pairing Sums
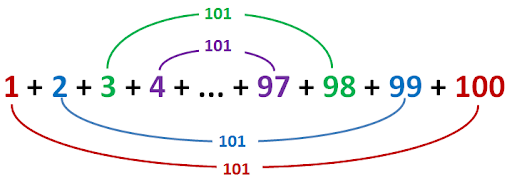
Theorem sum_to_n_shortcut_works:
forall (n: nat),
2 * sum_to_n n = n * (S n)."the overall payoff in terms of student engagement and performance on exams far exceeded my hopes"
- Using a Proof Assistant to Teach Programming Language Foundations
"Experience shows that many students do not have a very clear view of what is a proof" - Toward the use of a proof assistant to teach mathematics
"Computerized feedback ... can ease the burden on instructors and help students learn more efficiently." - Thesis - Andrew J. Haven (MIT)
Teaching Assistant
Curry-Howard Isomorphism

Inductive Predicates Demo
Free Book:
Theorem contains_correct:
forall (x: string) (xs: list string),
contains x xs = true <-> Contains x xs.
Proof.
...
Inductive BonusPoints ...: Prop :=
| bonus_points:
Contains you all_contributors ->
BonusPoints you all_contributors.
Law of Excluded Middle
Theorem lem: forall (A: Prop), A \/ not A.
Proof.
(* Calculus of Inductive Constructions *)
Abort.- Classical math misses the notion of uncomputable functions
- Constructive math ≈ programming
5 Stages of Accepting Constructive Math
Five Stages of Accepting Constructive Mathematics - Andrej Bauer
Theorem proof_by_contradiction:
forall P, not not P -> P."I want to prove that this diagram commutes,
lets suppose it doesn't" - no Category Theorist ever
"I need an algorithm, lets suppose it is not computable" - no Computer Scientist ever
Our work on Regexes
Regex
Set of Strings
Derived
Regex
Derived
Set Of Strings
- LEM for Regexes
- Coinduction for Finite number of states
derive
Derive
denote
denote
Quick Start
Recommended Start
- Coq Art Book: Interactive Theorem Proving and Program Development
Coq'Art: The Calculus of Inductive Constructions -
Yves Bertot and Pierre Castéran - Download Coq
- VSCode (VSCoq) or
Emacs (Proof General)

More Pie
Proof Assistants
- Lean
- Isabelle
- Coq
Dependent Types
- Adga
- Idris
- Pie
Dependent Types?
- Scala
- Haskell
- Typescript

Qed.
Thank you for providing input for this presentation