Modularization of Algorithms on
Complex Data Structures
An Encoding of
Typesafe
Extensible
Functional
Objects
Jonathan Immanuel Brachthäuser

Duality
Allowing modularly defined
folds (tree traversals) by choosing a
first-class extensible representation of
algebras.

Duality
Allowing modularly defined
folds (tree traversals) by choosing a
first-class extensible representation of
algebras.
Allowing modularly defined
unfolds (object definitions) by choosing a
first-class extensible representation of
coalgebras.
vs.





Extensibility at Runtime

In code
trait CoffeeMachine {
def makeCoffee: Coffee
}trait Grinder {
def grind(beans: Beans): Powder
}trait Steamer {
def steam: Steam
def foam(m: Milk): MilkFoam
}trait WaterLineConnected { self: CoffeeMachine => }trait EspressoMachine { self: CoffeeMachine with Compressor => }




Possible in Scala
new CoffeeMachine with Grinder with Steamer {}Not Possible In scAla
val cm = new CoffeeMachine
cm.makeCoffee
cm extends(Grinder) extends(Steamer)Aspects of modularity


Static Modularity
Temporal Modularity
Examples
Runtime Component Adaption
Incremental Construction
Monkey Patching
Debugging / Tracing
Our Solution
An Encoding of Functional Objects that is Typesafe and Extensible
Our Solution
An Encoding of Functional Objects that is Typesafe and Extensible
Why an encoding?
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
- Helps understanding a language feature by using already known semantics
- Can be used as a library, does not require a special compiler
- Allows reuse of existing infrastructure
- Flexibility to modify and experiment with the semantics
Why an encoding?
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
- Helps understanding a language feature by using already known semantics
- Can be used as a library, does not require a special compiler
- Allows reuse of existing infrastructure
- Flexibility to modify and experiment with the semantics
Encoding objects
In Scala?
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
What are Objects?
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
Interface
trait Counter {
def get: Int
def inc: Unit
}Implementation
trait CounterImpl extends Counter {
var count: Int // state
def get: Int = count
def inc: Unit = { count += 1 }
}Instantiation
def newCounter(init: Int): Counter =
new CounterImpl { var count = init }Infinite tree of observations
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE

val c = newCounter(0) // c0
c.get //=> 0
c.inc // c1
c.get //=> 1
c.inc // c2
// ...ScalA
Encoding
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait Counter {
def get: Int
def inc: Unit
}trait CounterF[State] {
def get: Int
def inc: State
}Interface
Endofunctor
ScalA
Encoding
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait Counter {
def get: Int
def inc: Unit
}trait CounterF[State] {
def get: Int
def inc: State
}trait CounterImpl extends Counter {
var count: Int
def get: Int = count
def inc: Unit = { count += 1 }
}val CounterImpl = count => new CounterF[Int] {
def get: Int = count
def inc: Int = count + 1
}Interface
Endofunctor
Implementation
Coalgebra
ScalA
Encoding
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait Counter {
def get: Int
def inc: Unit
}trait CounterF[State] {
def get: Int
def inc: State
}trait CounterImpl extends Counter {
var count: Int
def get: Int = count
def inc: Unit = { count += 1 }
}val CounterImpl = count => new CounterF[Int] {
def get: Int = count
def inc: Int = count + 1
}def newCounter(init: Int): Counter =
new CounterImpl { var count = init }def newCounter(init: Int): Fix[CounterF] =
unfold(CounterImpl, init)Interface
Endofunctor
Implementation
Coalgebra
Instantiation
Unfolding
Coalgebraic Encoding
In a Nutshell
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
val obj: Fix[F] = unfold(impl: S => F[S], init: S)fixed point
coalgebra
inital state
interface functor
Modularization
Split object implementation into modular components.
Use late bound self-references to articulate dependencies.
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
Modularization
Split object implementation into modular components.
Use late bound self-references to articulate dependencies.
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait OpenCoAlg[Self[_], Prov[_], S] {
def apply[T](priv: Lens[T, S]): CoAlg[Self, T] => CoAlg[Prov, T]
}provided interface
required interface
late bound self-reference
type CoAlg[F[_], S] = S => F[S]Modularization
Split object implementation into modular components.
Use late bound self-references to articulate dependencies.
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait OpenCoAlg[Self[_], Prov[_], S] {
def apply[T](priv: Lens[T, S]): CoAlg[Self, T] => CoAlg[Prov, T]
}provided interface
required interface
late bound self-reference
type CoAlg[F[_], S] = S => F[S]type CompleteCoAlg[F[_], S] = OpenCoAlg[F, F, S]An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait SkipF[State] {
def skip: State
}Example For Static Extensibility
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
trait SkipF[State] {
def skip: State
}val SkipImpl = new OpenCoAlg[CounterF, SkipF, Unit] {
def apply[S](priv: Lens[S, Unit]) = self => state => new SkipF[S] {
def skip = self.apply(self.apply(state).inc).inc
}
}Example For Static Extensibility
dependency on Counter
using it in the implementation
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
val CounterImpl = ...
val SkipImpl = ...
val both = compose(
CounterImpl,
SkipImpl)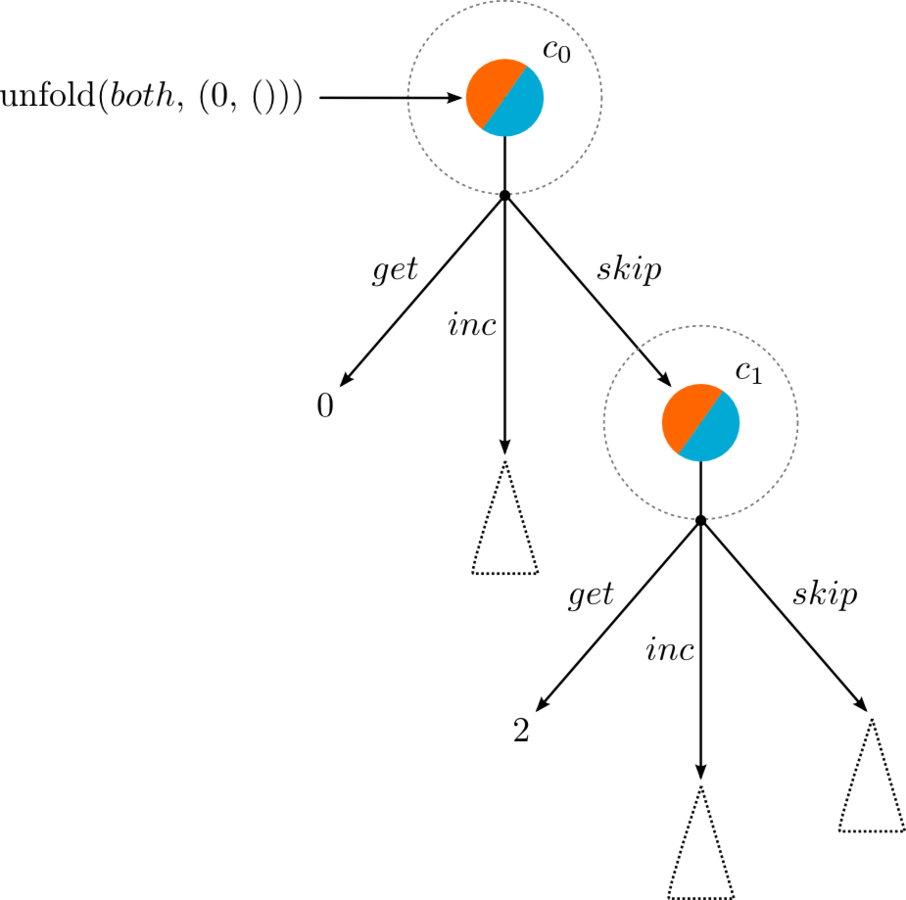
Instantiating the Composite
What about Extensibility?
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
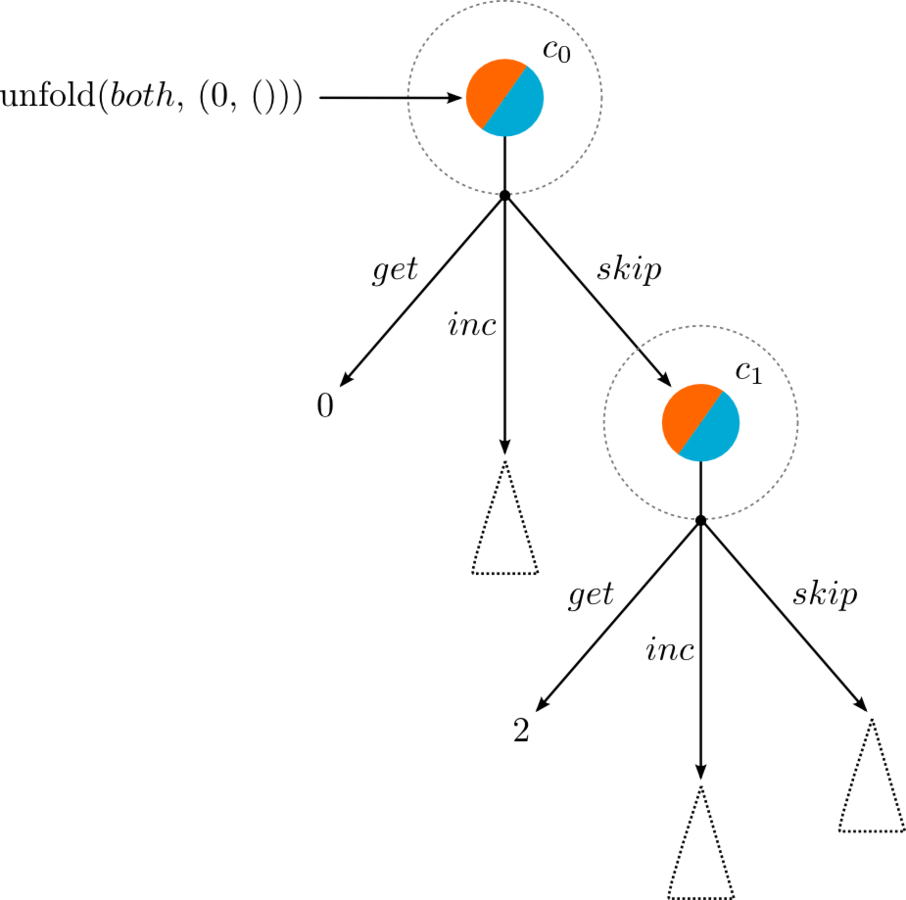
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
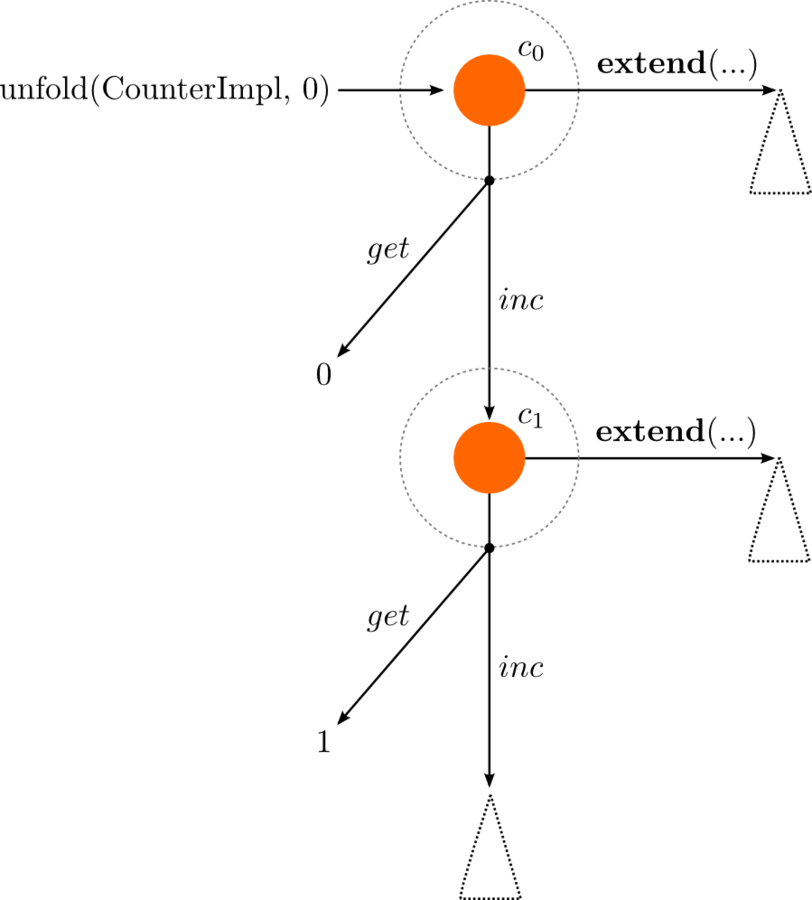
val c0 = unfold(CounterImpl, 0)
val c1 = c0.out.incAn encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
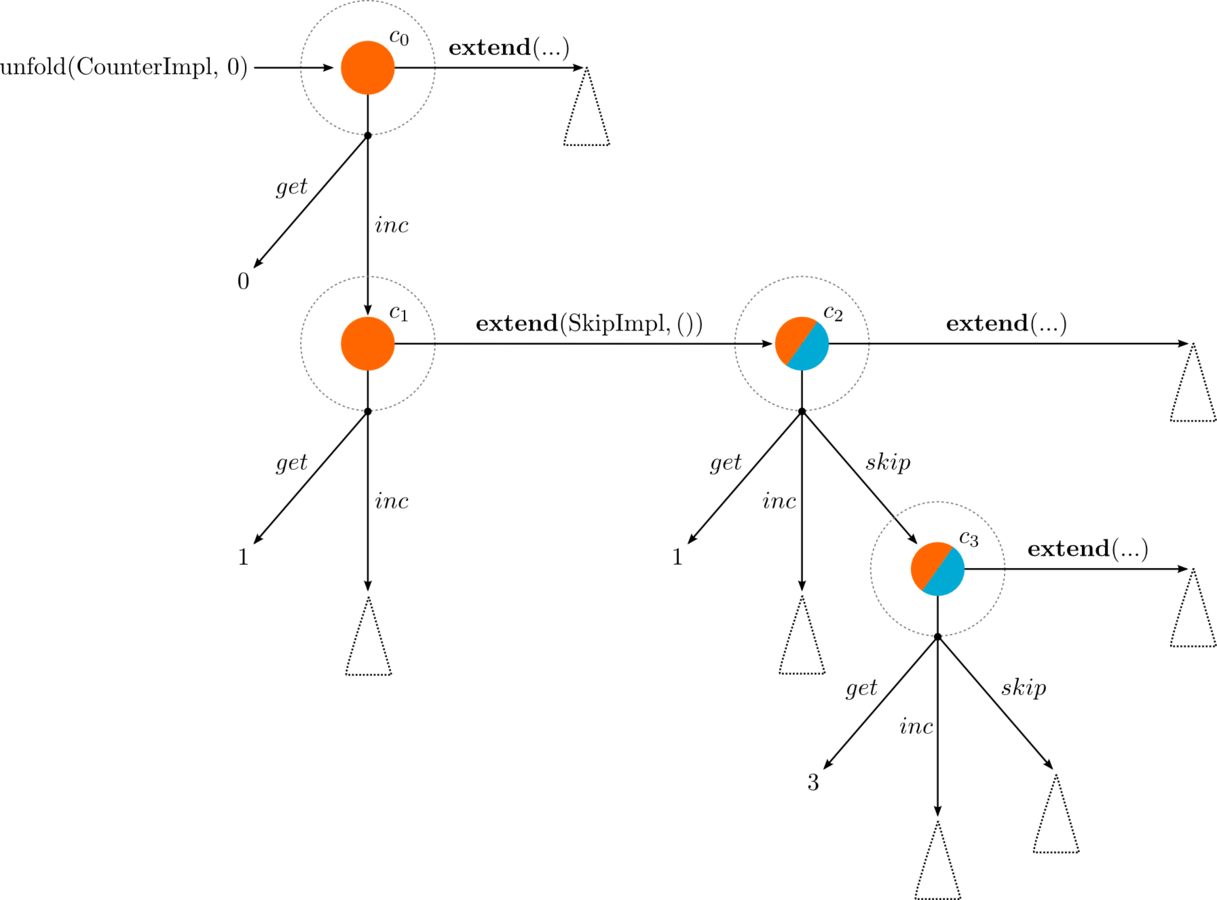
val c0 = unfold(CounterImpl, 0)
val c1 = c0.out.inc
val c2 = c1.extend(SkipImpl, ())
val c3 = c2.out.skipThe type changes: Fix[CounterF] to Fix[CounterF with SkipF]
An encoding of FUNCTIONAL OBJECTS THAT IS TYPESAFE AND EXTENSIBLE
unfold(co1, s1) extend(co2, s2)
is implemented by
unfold(compose(co1, co2), (s1, s2))
The extensibility is enabled by...
... defining static composition of coalgebra components:
1. by pointwise application with the tupled state,
2. composing the resulting interface implementations.
... implementing extend in terms of compose, thus
NoW Possible In scAla
val cm1 = unfold( CoffeeMachine )
val cm2 = cm1.makeCoffee
val cm3 = cm2 extends(Grinder) extends(Steamer)Extensions to the ENcoding
- Allow references to the extended base coalgebra,
imitating super-calls.
- Allow selective open-recursion by passing the current
as well as the late bound self-reference.
Conclusions
We have shown
- how to encode extensible objects in Scala.
It seems
- that object algebras can be dualized meaningfully.
In the future
- we would like to investigate the duality formally,
- improve the usability by optimizing performance and
syntactic overhead.
Thank you!