Research

• We need an optimal strategy
• There are two existing strategies
• Both of them are using T-Splines

The 1st Strategy

• Utilizes h refinements and T-spline basis functions

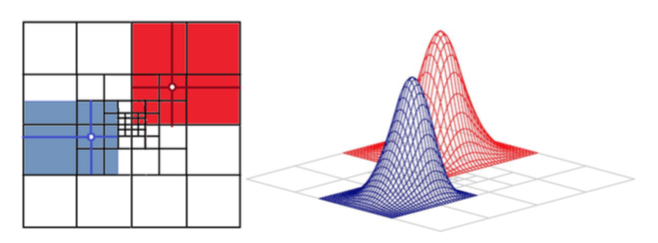
• For the point singularity the supports of T-spline basis functions from all the levels of the mesh overlap, which results in O(N^3) computational complexity of the solution

The 2nd Strategy

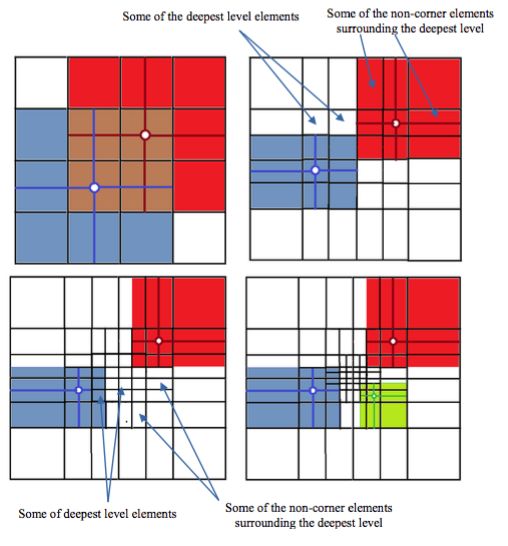
• additional h refinements to the first one, so that T-spline basis functions do not overlap and therefore the computational complexity is reduced to O(N)
• N for the second strategy is larger than for the first one

The 3rd Strategy

• No global C1 continuity of the solution anymore
• The third adaptive strategy uses h refinements with B-spline basis functions [1 and C0 separators (recursively repeated knots). 

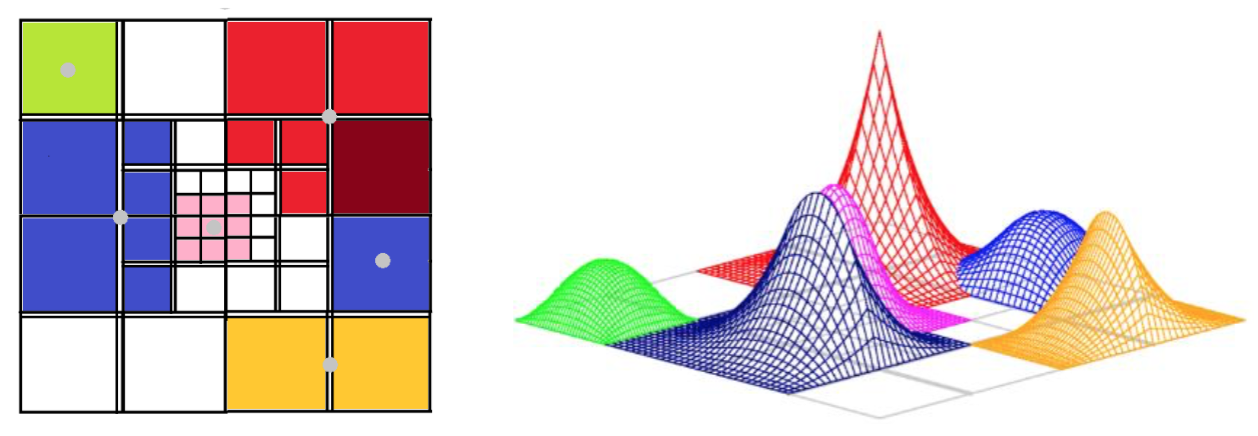
• We show that the computational cost of the third strategy is also linear, but we no longer preserve C1 global continuity of the solution

Code

Computations

• The 1st Strategy

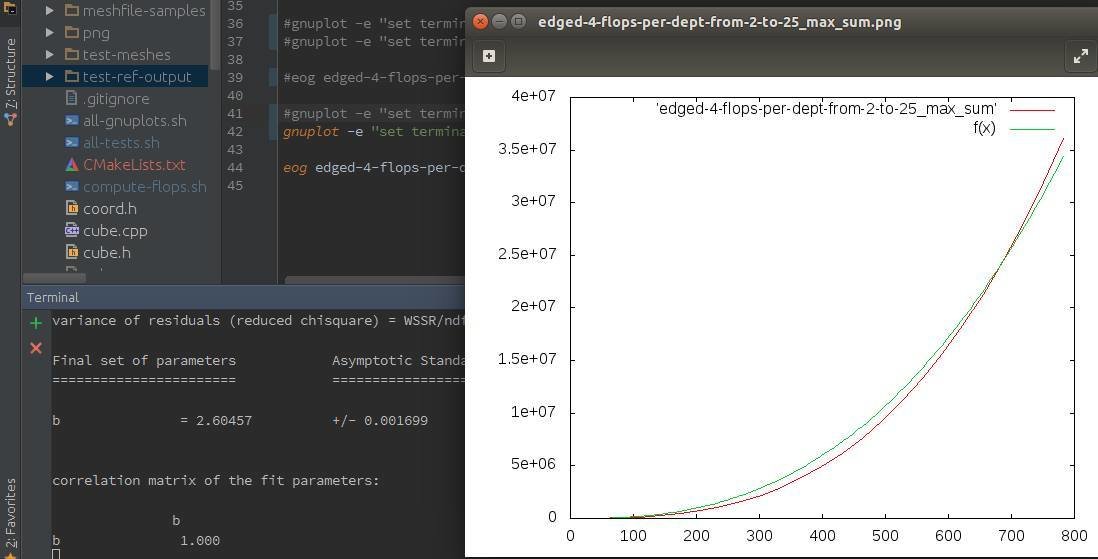
Computations

• The 1st Strategy

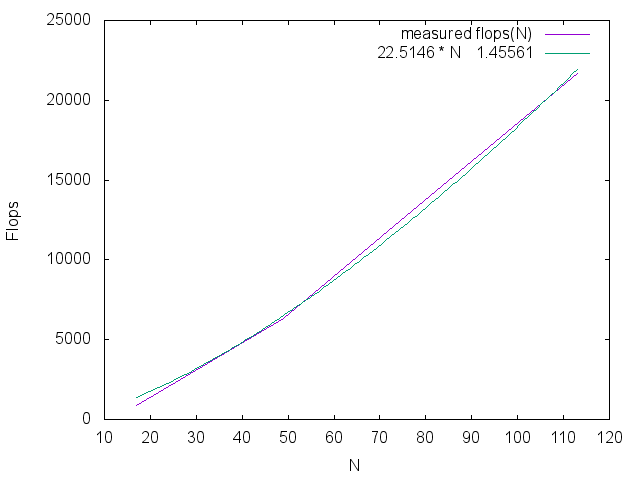
Abstract

Paper