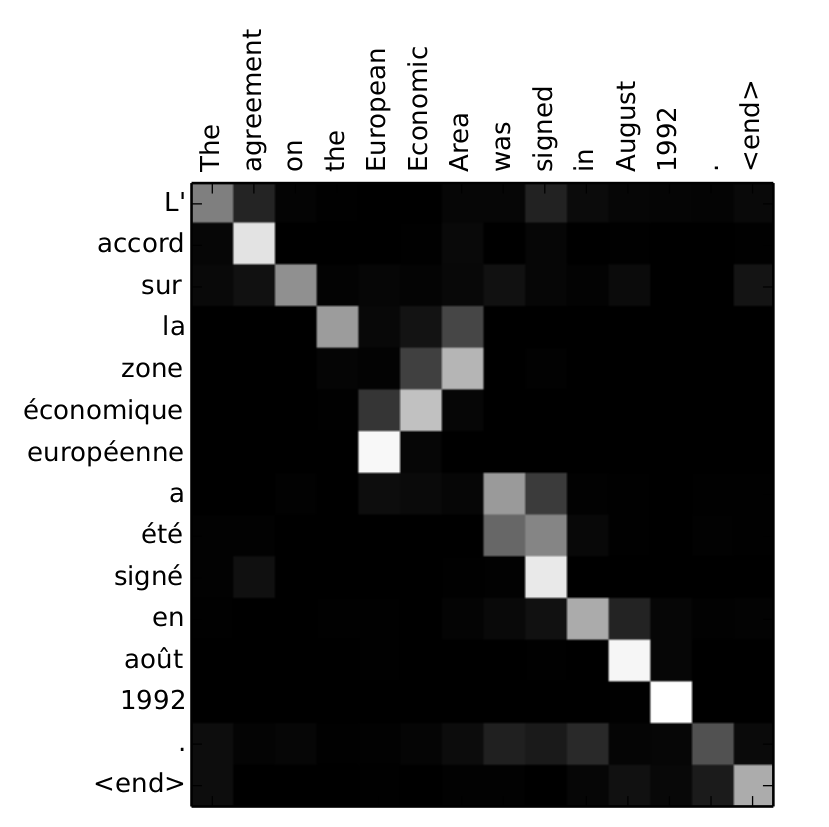Atenção

Overview

  • Motivação

  • O que é atenção?

  • Funções score

  • Atenção Global e Local

  • Atenção visual

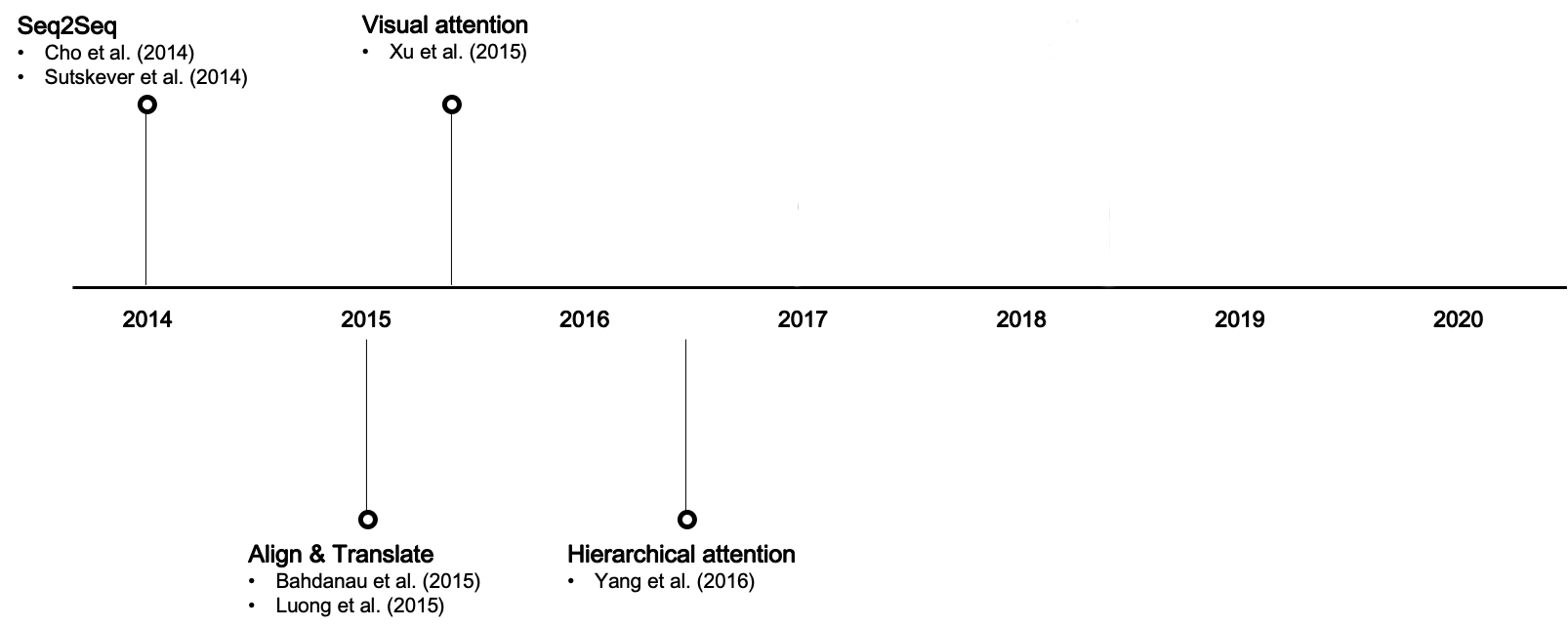
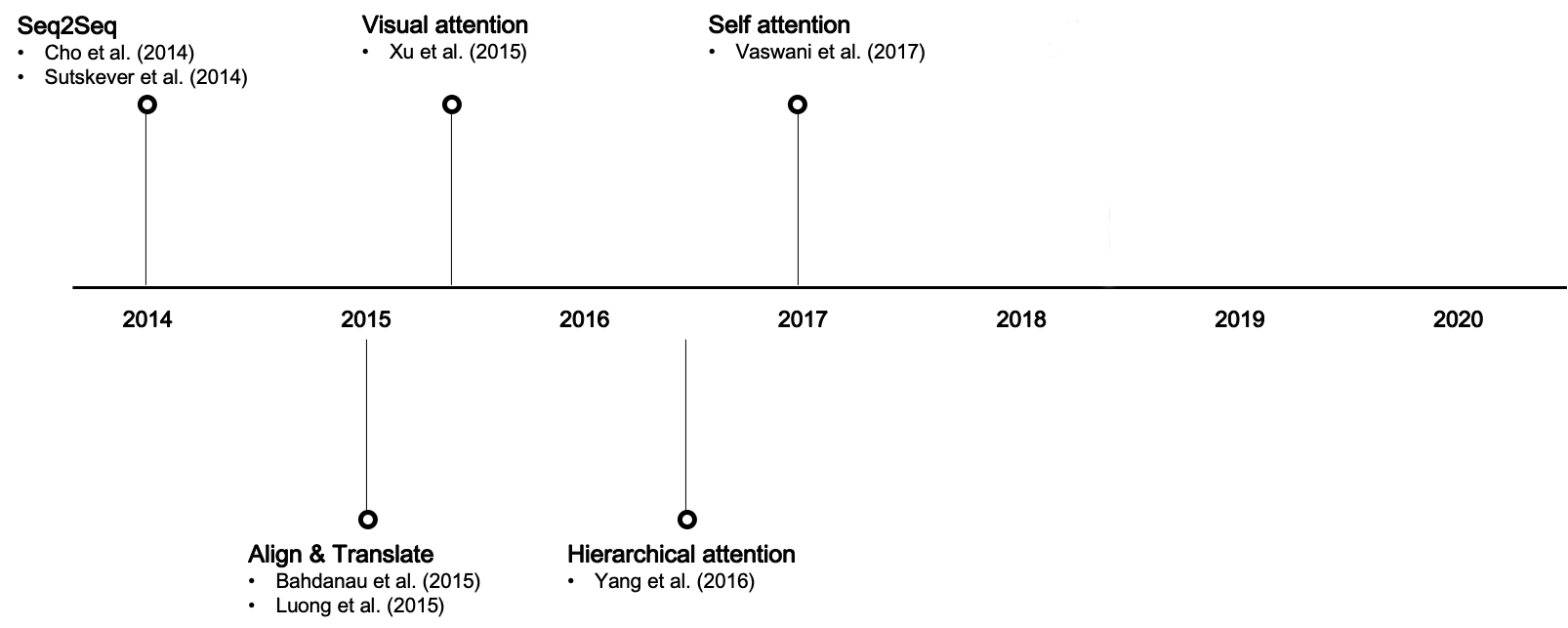
  • Atenção hierárquica

 

Motivação

Como vimos, redes recorrentes apresentam dificuldades  em capturar relações de longa distância.

LSTM e GRU ajudam mas não resolvem o problema completamente.

 

Intuição: seq2seq não captura a estrutura interna da linguagem

Motivação

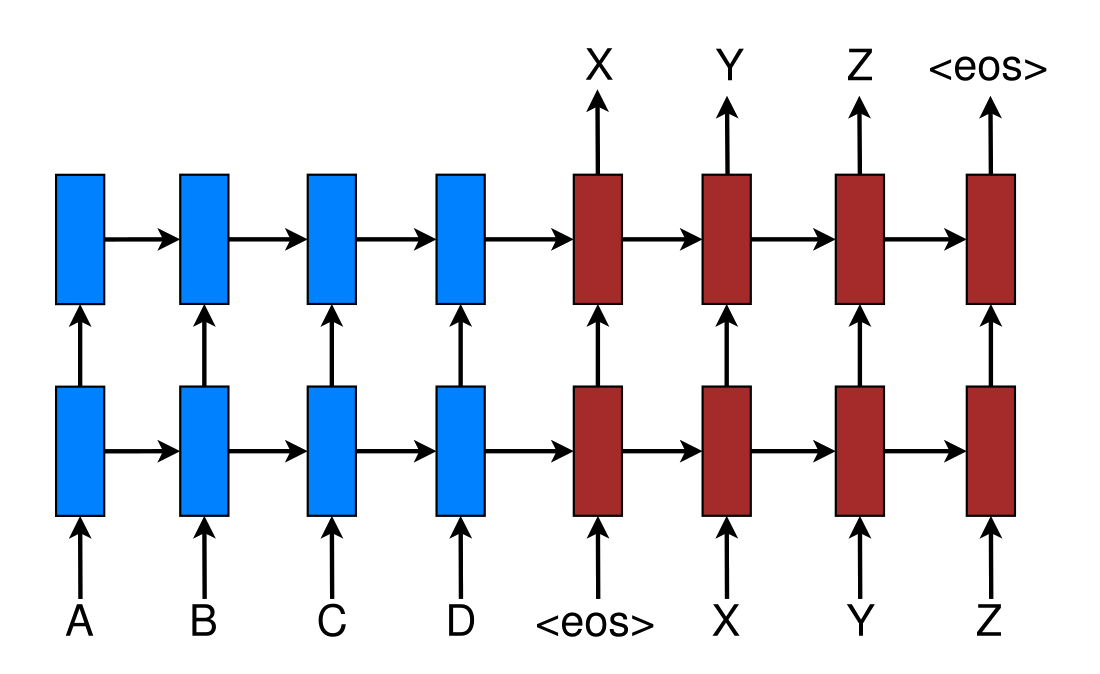
Todo encoder-decoder possui um gargalo informacional, toda informação capturada no encoder deve ser representada em apenas um vetor.


 

Como podemos melhorar isso?

Atenção

Intuitivamente, atenção pode ser vista como uma medida de relevância entre os elementos de um input e de um output.

Nos permite capturar o contexto mais relevante para cada etapa do decoder, de maneira independente da distância entre os tokens.

Em termos estatísticos, atenção mede correlação.

Atenção

 

No contexto de traduções, atenção também pode ser vista como uma espécie de alinhamento.

 

Ok, mas e como calculamos atenção?

Existem diversas variações do conceito de atenção. Mas todos seguem um mesmo esqueleto para se chegar em pesos de atenção.

Um modelo genérico de Atenção

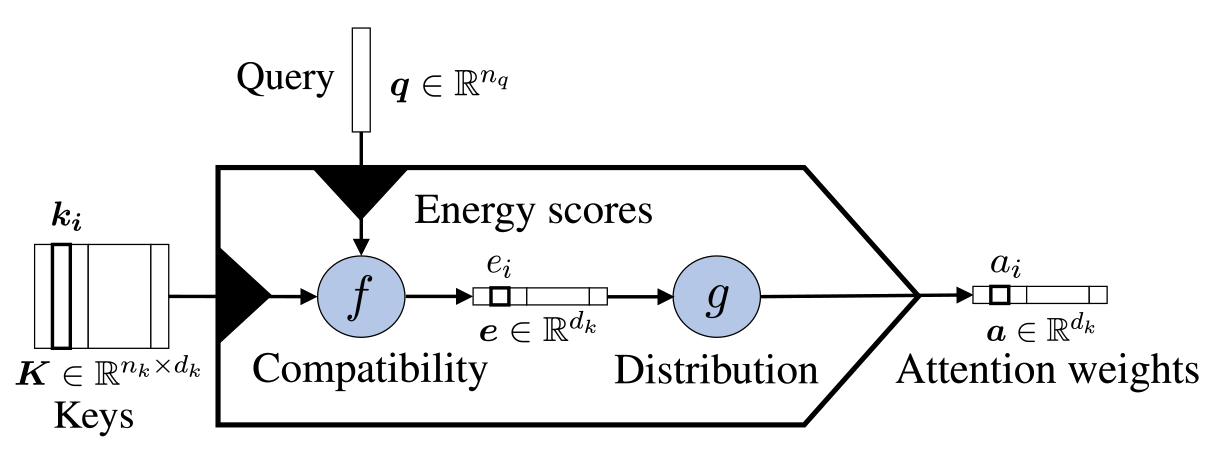
De maneira geral, para criar um modelo de atenção é necessário definir 3 coisas:

  • Key, Query, Value

  • Função Score

  • Função de Distribuição

Key, Query & Value

Key e Query são os parâmetros da função score, são os objetos sobre os quais desejamos calcular a atenção, ou seja, correlacionar numericamente.

 

Keys e Values podem ser os mesmos elementos (como em Luong et. al. 2015)

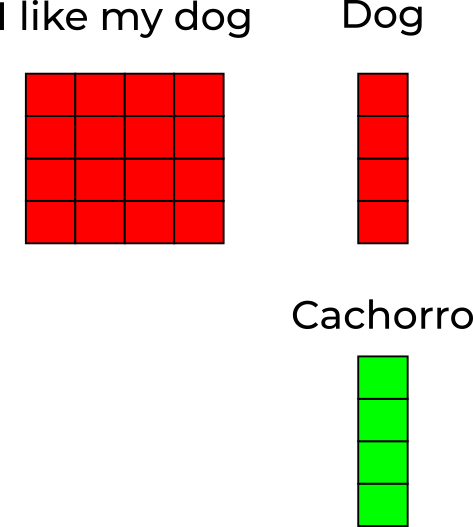
Value são os valores em que aplicaremos os pesos de atenção calculados.

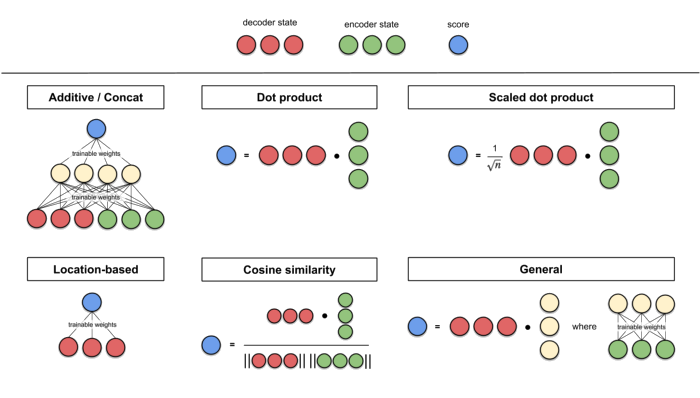
Funções Score

Funções de distribuição

Definem a distribuição dos pesos de atenção, sendo Softmax a mais tradicional.

 

Também pode ser utilizado para delimitar o escopo da atenção (global vs local).

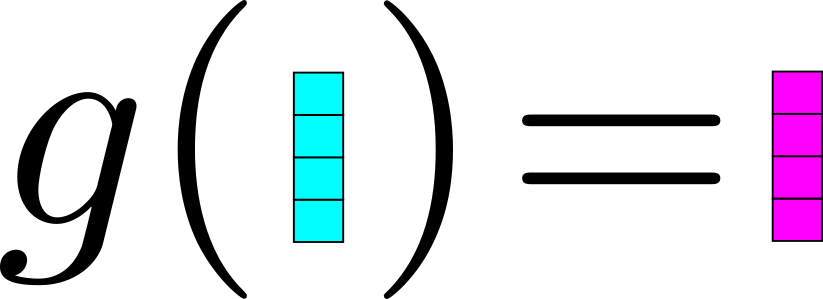
Um exemplo:

Luong et. al. 2015

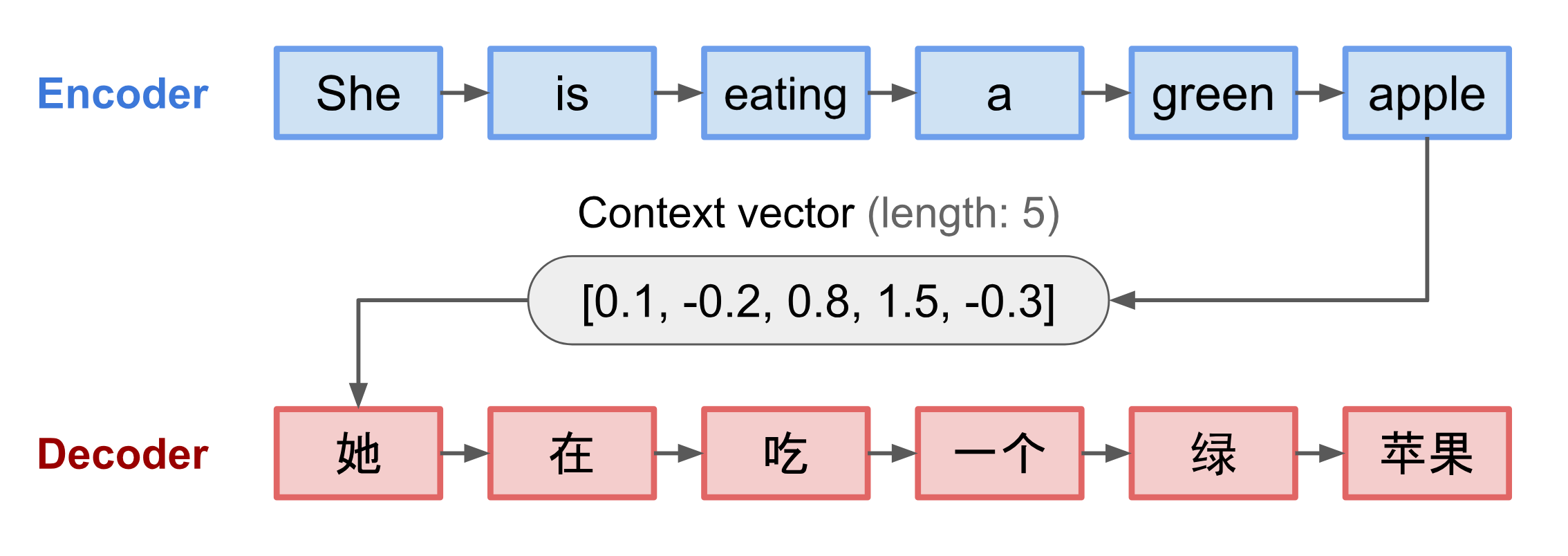
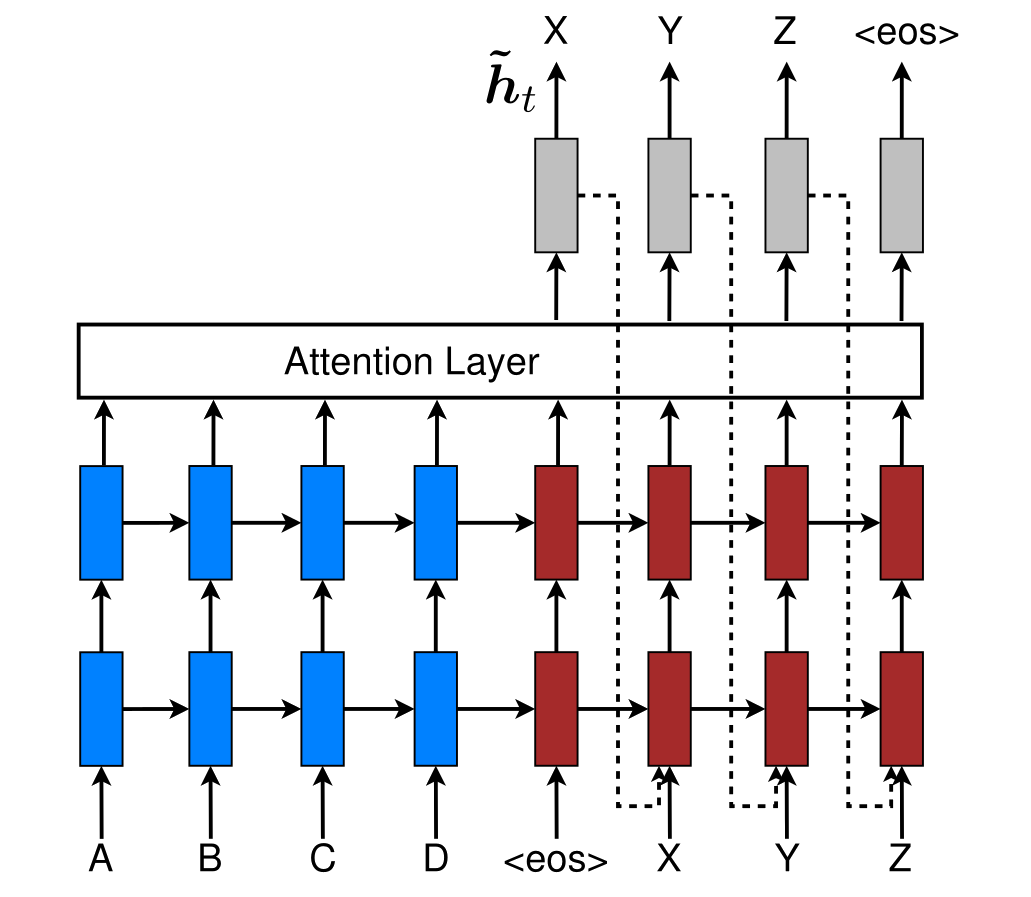
Vamos tomar uma arquitetura encoder decoder comum: um único código para a sentença de entrada

E adicionar uma camada de atenção.

Um código adaptado para cada token de saída

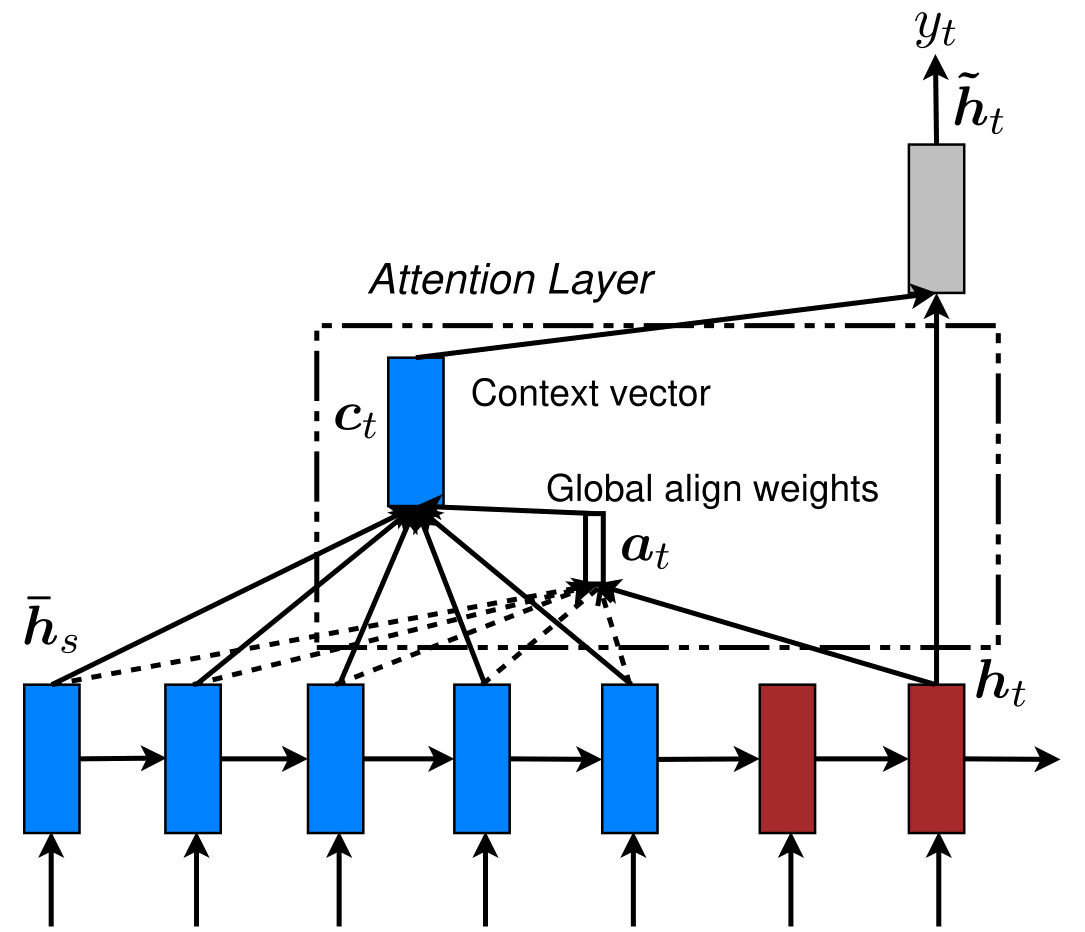
A cada etapa nós utilizamos um vetor contexto \(C_t\) e o \(h_t\) anterior para calcularmos a palavra seguinte \(y_t\).

\(C_t\) é específico para cada etapa e é calculado a partir do \(h_t\) atual do decoder (Query) e todos os \(\bar{h}_s\) do encoder (Keys).

 

Para cada par \((h_t, \bar{h}_s)\) nós calculamos seu score

score(h_t, \bar{h}_s) = h_t^\top \bar{h}_s

E então calculamos o softmax de todos eles

a_t(s)= \frac{exp(score(h_t, \bar{h}_{s}))}{\sum_{{{s}}'} exp(score(h_t, \bar{h}_{{s}'}))}

Após obtermos os pesos de atenção \(a_t\), podemos calcular \(c_t\) ao tomarmos a média ponderada dos \(\bar{h}_s\) do encoder (Values)
 

c_t =\frac{\sum_s \bar{h}_i a_i}{|s|}

Essa matriz representa os pesos \(a_t\) para cada etapa de tradução.

Um modelo genérico de Atenção

  • Key, Query, Value

  • Função Score

  • Função de Distribuição

Luong et. al. 2015

  • Key, Query, Value              

  • Função Score                      

  • Função de Distribuição      

\((\bar{h}_s,h_t,\bar{h}_s )\)

produto escalar

softmax

Um modelo genérico de Atenção

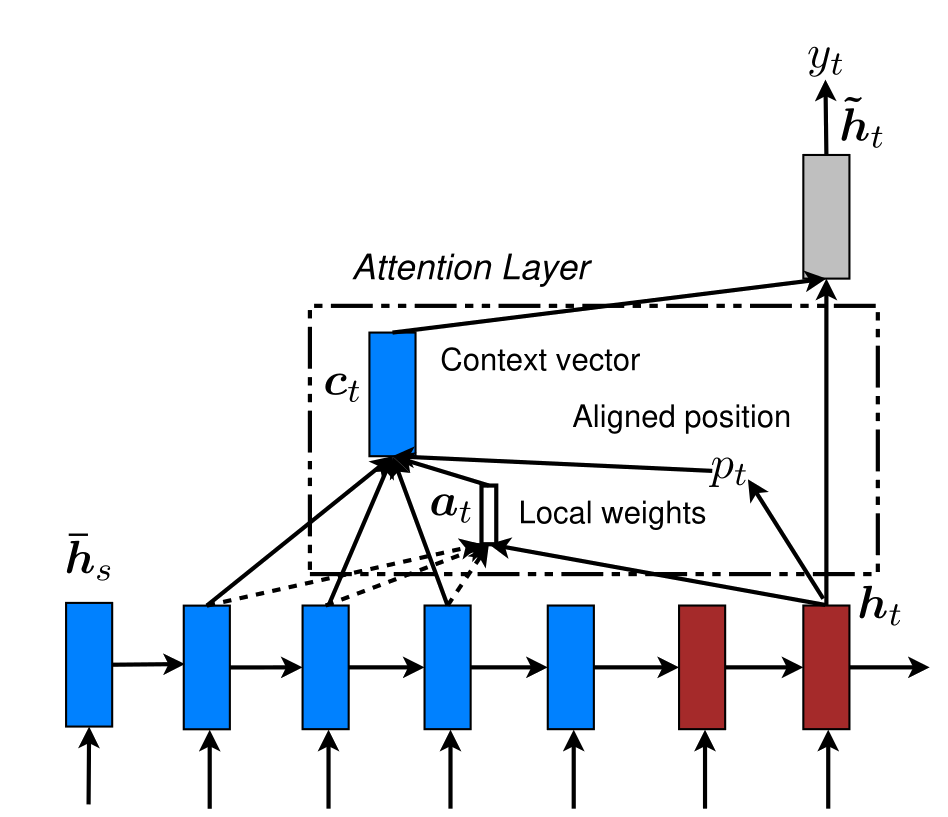
Global

Local

Modelo Formal de Atenção

Considere \(h_1 , \ldots , h_k\) os estados escondidos do encoder e  \(h'_1 , \ldots , h'_m\) os do decoder

 

$$\hat{y}_t = {softmax}(W h_t +b)$$

\(\tilde{h}_t = {tanh}(W_x[c_t;h'_t]+b_x)\)

\(c_t = attend(h_1, \ldots, h_k, h'_t)\)

\(h'_t = f_{dec}(x'_t,h'_{t-1})\)

\( x'_t = word2vec(y_{t-1})\)

Foco na Atenção

\(attend(h_1, \ldots, h_k, h'_t) = \sum_{i=1}^{k} \alpha_{t,i} \cdot h_i\)

\[\alpha_t = softmax[s_1\\\qquad\vdots\\\qquad s_k]\]

\[s_i = score(h'_t,h_i)\]

\(score(h'_h,h_i) = h'_t{}^\top\cdot h_i\)

Atenção Visual

Atenção nos permite associar partes do input mais importantes para o output. Por exemplo, qual legenda você daria para essas fotos?

 

Atenção Visual

E agora?

Atenção Visual

Atenção nos ajuda a interpretar melhor nossos modelos e entender qual foi seu processo de decisão.

Atenção Visual

Atenção nos ajuda a interpretar melhor nossos modelos e entender qual foi seu processo de decisão.

A dog is standing on a hardwood floor.

Global

Local

Atenção Hierárquica

Self-Attention & Transformer

Próxima aula!