DEEP LEARNING FOR MEDICAL DATA

Andrew Beam, PhD

Department of Biomedical Informatics

February 23rd, 2018

twitter: @AndrewLBeam

WHAT IS DEEP LEARNING?

WHAT IS DEEP LEARNING?

Deep learning is a specific kind of machine learning

- Machine learning automatically learns relationships using data

- Deep learning refers to large neural networks 

- These neural networks have millions of parameters and hundreds of layers (e.g. they are structurally deep)

- Most important: Deep learning is not magic!

WHAT IS A NEURAL NET?

NEURAL NETWORK STRUCTURE

NEURAL NETWORK STRUCTURE

Say we want to build a model to predict the likelihood of a have a heart attack (MI) based on blood pressure (BP) and BMI 

NEURAL NET STRUCTURE

A neural net is a modular way to build a classifier

BP
BPBP
BMI
BMIBMI

Inputs

Output

Probability of MI

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

Inputs

Output

BP
BPBP
BMI
BMIBMI

Probability of MI

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

A neuron does two things, and only two things

BP
BPBP
BMI
BMIBMI

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

Weight for

A neuron does two things, and only two things

Weight for

1) Weighted sum of inputs

w_1*BP + w_2*BMI
w1∗BP+w2∗BMIw_1*BP + w_2*BMI
BP
BPBP
BMI
BMIBMI
BP
BPBP
BMI
BMIBMI

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

Weight for

A neuron does two things, and only two things

Weight for

1) Weighted sum of inputs

\phi(w_1*BP + w_2*BMI)
ϕ(w1∗BP+w2∗BMI)\phi(w_1*BP + w_2*BMI)

2) Nonlinear transformation

BP
BPBP
BMI
BMIBMI
BP
BPBP
BMI
BMIBMI
w_1*BP + w_2*BMI
w1∗BP+w2∗BMIw_1*BP + w_2*BMI

WHAT IS AN ARTIFICIAL NEURON?

\phi()
ϕ()\phi()

is known as the activation function

Sigmoid

Hyperbolic Tangent

WHAT IS AN ARTIFICIAL NEURON?

Summary: A neuron produces a single number that is a nonlinear transformation of its input connections

A neuron does two things, and only two things

= a number

BP
BPBP
BMI
BMIBMI

WHAT IS AN ARTIFICIAL NEURON?

Summary: A neuron produces a single number that is a nonlinear transformation of its input connections

A neuron does two things, and only two things

= a number

BP
BPBP
BMI
BMIBMI

This simple formula allows for an amazing amount of expressiveness

PERCEPTRON BY HAND

PERCEPTRONS

Let's say we'd like to have a single neural learn a simple function

y

X_1
X1X_1
X_2
X2X_2
X1 X2 y
0 0 0
0 1 1
1 0 1
1 1 1
w_1
w1w_1
w_1
w1w_1
b
bb

Observations

PERCEPTRONS

How do we make a prediction for each observations?

y

X_1
X1X_1
X_2
X2X_2
X1 X2 y
0 0 0
0 1 1
1 0 1
1 1 1
w_1
w1w_1
w_1
w1w_1
b
bb

Assume we have the following values

w1 w2 b
1 -1 0

Observations

Predictions

For the first observation:

Assume we have the following values

w1 w2 b
1 -1 0
X_1 = 0, X_2 = 0, y =0
X1=0,X2=0,y=0X_1 = 0, X_2 = 0, y =0

Predictions

For the first observation:

Assume we have the following values

w1 w2 b
1 -1 0
X_1 = 0, X_2 = 0, y =0
X1=0,X2=0,y=0X_1 = 0, X_2 = 0, y =0

First compute the weighted sum:

h = w_1*X_1 + w_2*X_2 + b
h=w1∗X1+w2∗X2+bh = w_1*X_1 + w_2*X_2 + b
h = 1*0 + -1*0 + 0 = 0
h=1∗0+−1∗0+0=0h = 1*0 + -1*0 + 0 = 0
h = 0
h=0h = 0

Predictions

For the first observation:

Assume we have the following values

w1 w2 b
1 -1 -0.5
X_1 = 0, X_2 = 0, y =0
X1=0,X2=0,y=0X_1 = 0, X_2 = 0, y =0

First compute the weighted sum:

h = w_1*X_1 + w_2*X_2 + b
h=w1∗X1+w2∗X2+bh = w_1*X_1 + w_2*X_2 + b
h = 1*0 + -1*0 + -0.5
h=1∗0+−1∗0+−0.5h = 1*0 + -1*0 + -0.5
h = -0.5
h=−0.5h = -0.5

Transform to probability:

p = \frac{1}{1+\exp(-h)}
p=11+exp(−h)p = \frac{1}{1+\exp(-h)}
p = \frac{1}{1+\exp(-0.5)}
p=11+exp(−0.5)p = \frac{1}{1+\exp(-0.5)}
p = 0.38
p=0.38p = 0.38

Predictions

For the first observation:

Assume we have the following values

w1 w2 b
1 -1 -0.5
X_1 = 0, X_2 = 0, y =0
X1=0,X2=0,y=0X_1 = 0, X_2 = 0, y =0

First compute the weighted sum:

h = w_1*X_1 + w_2*X_2 + b
h=w1∗X1+w2∗X2+bh = w_1*X_1 + w_2*X_2 + b
h = 1*0 + -1*0 + -0.5
h=1∗0+−1∗0+−0.5h = 1*0 + -1*0 + -0.5
h = -0.5
h=−0.5h = -0.5

Transform to probability:

p = \frac{1}{1+\exp(-h)}
p=11+exp(−h)p = \frac{1}{1+\exp(-h)}
p = \frac{1}{1+\exp(-0.5)}
p=11+exp(−0.5)p = \frac{1}{1+\exp(-0.5)}
p = 0.38
p=0.38p = 0.38

Round to get prediction:

\hat{y} = round(p)
y^=round(p)\hat{y} = round(p)
\hat{y} = 0
y^=0\hat{y} = 0

Predictions

Putting it all together:

h = w_1*X_1 + w_2*X_2 + b
h=w1∗X1+w2∗X2+bh = w_1*X_1 + w_2*X_2 + b
p = \frac{1}{1+\exp(-h)}
p=11+exp(−h)p = \frac{1}{1+\exp(-h)}
\hat{y} = round(p)
y^=round(p)\hat{y} = round(p)

Assume we have the following values

w1 w2 b
1 -1 -0.5
X1 X2 y h p
0 0 0 -0.5 0.38 0
0 1 1
1 0 1
1 1 1
\hat{y}
y^\hat{y}

Fill out this table

Room for Improvement

Our neural net isn't so great... how do we make it better?

 

 

What do I even mean by better?

Room for Improvement

Let's define how we want to measure the network's performance.

 

There are many ways, but let's use squared-error:

 

 

 

(y - p)^2
(y−p)2(y - p)^2

Room for Improvement

Let's define how we want to measure the network's performance.

 

There are many ways, but let's use squared-error:

 

 

 

Now we need to find values for                  that make this error as small as possible

(y - p)^2
(y−p)2(y - p)^2
w_1, w_2, b
w1,w2,bw_1, w_2, b

ALL OF ML IN ONE SLIDE

Our task is learning values for                 such the the difference between the predicted and actual values is as small as possible.

w_1, w_2, b
w1,w2,bw_1, w_2, b

Learning from Data

So, how we find the "best" values for 

w_1, w_2, b
w1,w2,bw_1, w_2, b

Learning from Data

So, how we find the "best" values for 

 

hint: calculus

w_1, w_2, b
w1,w2,bw_1, w_2, b

Learning from Data

Recall (without PTSD) that the derivative of a function tells you how it is changing at any given location.

 

If the derivative is positive, it means it's going up.

 

If the derivative is negative, it means it's going down. 

Learning from Data

Simple strategy:

​​- Start with initial values for

- Take partial derivatives of loss function

with respect to

- Subtract the derivative (also called the gradient) from each

w_1, w_2, b
w1,w2,bw_1, w_2, b
w_1, w_2, b
w1,w2,bw_1, w_2, b

Learning Rules for each Parameter

gw_1 = (p - y)*(p*(1-p)*X_1)
gw1=(p−y)∗(p∗(1−p)∗X1)gw_1 = (p - y)*(p*(1-p)*X_1)
gw_2 = (p - y)*(p*(1-p)*X_2)
gw2=(p−y)∗(p∗(1−p)∗X2)gw_2 = (p - y)*(p*(1-p)*X_2)
g_b = (p - y)*(p*(1-p))
gb=(p−y)∗(p∗(1−p))g_b = (p - y)*(p*(1-p))

Gradient for 

Gradient for 

Gradient for 

w^{new}_1 = w^{old}_1 - \sum gw_1
w1new=w1old−∑gw1w^{new}_1 = w^{old}_1 - \sum gw_1

Update for 

Update for 

Update for 

w^{new}_2 = w^{old}_2 - \sum gw_2
w2new=w2old−∑gw2w^{new}_2 = w^{old}_2 - \sum gw_2
b^{new} = b^{old} - \sum g_b
bnew=bold−∑gbb^{new} = b^{old} - \sum g_b
w_1
w1w_1
w_1
w1w_1
w_2
w2w_2
w_2
w2w_2
b
bb
b
bb

Learning Rules for each Parameter

gw_1 = (p - y)*(p*(1-p)*X_1)
gw1=(p−y)∗(p∗(1−p)∗X1)gw_1 = (p - y)*(p*(1-p)*X_1)
gw_2 = (p - y)*(p*(1-p)*X_2)
gw2=(p−y)∗(p∗(1−p)∗X2)gw_2 = (p - y)*(p*(1-p)*X_2)
g_b = (p - y)*(p*(1-p))
gb=(p−y)∗(p∗(1−p))g_b = (p - y)*(p*(1-p))

Gradient for 

Gradient for 

Gradient for 

w^{new}_1 = w^{old}_1 - \sum gw_1
w1new=w1old−∑gw1w^{new}_1 = w^{old}_1 - \sum gw_1

Update for 

Update for 

Update for 

w^{new}_2 = w^{old}_2 - \sum gw_2
w2new=w2old−∑gw2w^{new}_2 = w^{old}_2 - \sum gw_2
b^{new} = b^{old} - \sum g_b
bnew=bold−∑gbb^{new} = b^{old} - \sum g_b
w_1
w1w_1
w_1
w1w_1
w_2
w2w_2
w_2
w2w_2
b
bb
b
bb

Fill in new table!

A Simple Perceptron in R

train <- function(X,y,w,b,iter=10,lr=1) {
  w_new <- w
  b_new <- b
  for(i in 1:iter) {
    preds <- plogis(X %*% w_new + b_new)

    grad_w1 <- (preds - y)*preds*(1 - preds)*X[,1]
    grad_w2 <- (preds - y)*preds*(1 - preds)*X[,2]
    grad_b <- (preds - y)*(preds*(1 - preds))
    
    w_new[1] <- w_new[1] - lr*sum(grad_w1)
    w_new[2] <- w_new[2] - lr*sum(grad_w2)
    b_new <- b_new - lr*sum(grad_b)
    error <- (y - preds)^2
    print(paste0("Error at iteration ",i,": ",mean(error)))
  }
  return(list(w=w_new,b=b_new))
}

X <- rbind(c(0,0),c(0,1),c(1,0),c(1,1))
y <- c(0,1,1,1)
w <- as.vector(c(1,-1))
b <- -0.5

train(X,y,w,b)

Another Example

X1 X2 y
0 0 0
0 1 0
1 0 0
1 1 1

Final Example

X1 X2 y
0 0 0
0 1 1
1 0 1
1 1 0

What Happened?

Why didn't this work?

What Happened?

Why didn't this work?

Is this relationship "harder" in some sense?

What Happened?

Why didn't this work?

Is this relationship "harder" in some sense?

Let's plot it and see.

NEURAL NETWORK STRUCTURE

BP
BPBP
BMI
BMIBMI

Inputs

Output

Neural nets are organized into layers

Probability of MI

NEURAL NETWORK STRUCTURE

BP
BPBP
BMI
BMIBMI

Inputs

Output

Neural nets are organized into layers

Probability of MI

NEURAL NETWORK STRUCTURE

Inputs

Output

Input Layer

Neural nets are organized into layers

BP
BPBP
BMI
BMIBMI

Probability of MI

NEURAL NETWORK STRUCTURE

Inputs

Output

Neural nets are organized into layers

1st Hidden Layer

Input Layer

BP
BPBP
BMI
BMIBMI

Probability of MI

NEURAL NETWORK STRUCTURE

Inputs

Output

Neural nets are organized into layers

A single hidden unit

1st Hidden Layer

Input Layer

BP
BPBP
BMI
BMIBMI

Probability of MI

NEURAL NETWORK STRUCTURE

Inputs

Output

Input Layer

Neural nets are organized into layers

1st Hidden Layer

A single hidden unit

2nd Hidden Layer

BP
BPBP
BMI
BMIBMI

Probability of MI

NEURAL NETWORK STRUCTURE

Inputs

Output

Input Layer

Neural nets are organized into layers

1st Hidden Layer

A single hidden unit

2nd Hidden Layer

Output Layer

BP
BPBP
BMI
BMIBMI

Probability of MI

IN CLASS ASSIGNMENT

MODERN DEEP LEARNING

Neural networks are one of the oldest ideas in machine learning and AI

- Date back to 1940s

- Long history of "hype" cycles - boom and bust

- Were *not* state of the are machine learning technique for most of their existence

- Why are they popular now?

MODERN DEEP LEARNING

Several key advancements have enabled the modern deep learning revolution

GPU enable training of huge neural nets on extremely large datasets

 

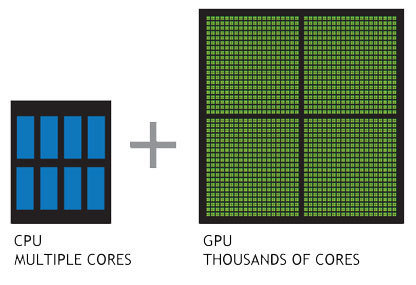
Several key advancements have enabled the modern deep learning revolution

MODERN DEEP LEARNING

Transfer Learning

Train big model

 

 

 

 

on large dataset

Refine model

 

 

 

 

on smaller dataset

Several key advancements have enabled the modern deep learning revolution

Methodological advancements have made deeper networks easier to train

 

Architecture

Optimizers

Activation Functions

MODERN DEEP LEARNING

Several key advancements have enabled the modern deep learning revolution

Easy to use frameworks dramatically lower the barrier to entry

Automatic differentiation allows easy prototyping

MODERN DEEP LEARNING

+

CONVOLUTIONAL NEURAL NETWORKS

CONVOLUTIONAL NEURAL NETS (CNNs)

Dates back to the late 1980s

  • Responsible for Deep Learning revival 
  • Invented by in 1989 Yann Lecun at Bell Labs - "Lenet"
  • Integrated into handwriting recognition systems
    in the 90s
  • Huge flurry of activity after the Alexnet paper

THE BREAKTHROUGH (2012)

Imagenet Database

  • Millions of labeled images
  • Objects in images fall into 1 of a possible 1,000 categories
  • Relatively high-resolution
  • Bounding boxes giving exact location of object - useful for both classification and localization

 Large Scale Visual

Recognition Challenge (ILSVRC)

  • ​Annual Imagenet Challenge starting in 2010
  • Successor to smaller PASCAL VOC challenge
  • Many tracks including classification and localization
  • Standardized training and test set. Competitors upload predictions for test set and are automatically scored

THE BREAKTHROUGH (2012)

Pivotal event occurred in 2012 which laid the blueprint for successful deep learning model

  • Massive amounts of labeled images
  • Training with GPUs
  • Methodological innovations that enabled training deeper networks while minimizing overfitting 

THE BREAKTHROUGH (2012)

In 2011, a misclassification rate of 25% was near state of the art on ILSVRC

 

In 2012, Geoff Hinton and two graduate students, Alex Krizhevsky and Ilya Sutskever, entered ILSVRC with one of the first deep neural networks trained on  GPUs, now known as "Alexnet"

 

Result: An error rate of 16%, nearly half what the second place entry was able to achieve.

The computer vision world immediately took notice

THE ILSVRC AFTERMATH (2012-2014)

Alexnet paper has ~ 16,000 citations since being published in 2012!

Most algorithms expect "tabular" data

WHY CNNS WORK

y X1 X2 X3 X4
0 7 52 17 654
0 23 2752 4 1
1 786 27 0 5
0 354 7527 89 68

The problem with tabular data

What is this a picture of?

WHY CNNS WORK

What is this a picture of?

The problem with tabular data

WHY CNNS WORK

What is this a picture of?

Tabular data throws away too much information!

The problem with tabular data

WHY CNNS WORK

CONVOLUTIONAL NEURAL NETS

Images are just 2D arrays of numbers

Goal is to build f(image) = 1

CONVOLUTIONAL NEURAL NETS

CNNs look at small connected groups of pixels using "filters"

Image credit: http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution

Images have a local correlation structure

 

Near by pixels are likely to be more similar than pixels that are far away

 

CNNs exploit this through convolutions of small image patches

WHY DO CNNs WORK SO WELL?

  • Based on solid image priors
  • Exploit properties of images, e.g. local correlations and invariances
  • ​Mimic generative distribution with augmentation to reduce over fitting
  • Results in end-to-end visual recognition system trained with SGD on GPUs: pixels in -> classifications out

CNNs exploit strong prior information about images

CASE STUDY

DIABETIC RETINOPATHY

In 2016 Google built a deep learning model to automatically diagnose patients with diabetic retinopathy

  • Input data: Labeled fundus photographs of the eye
  • ​Large database of 128,000 images they created for this project
  • Hired ophthalmologists to annotate the images ($$$)

DIABETIC RETINOPATHY

DIABETIC RETINOPATHY

Why did this work so well?

- Huge dataset of over 100,000 images

- High quality annotations - each image was rated by 3-7 opthamologists

- Transfer learning - neural network was originally trained on Imagenet!

- For the cost of a GPU (~$1,000) it's possible to read 240 million images/day at accuracy on par with best ophthalmologists!

DIABETIC RETINOPATHY

Implications

- Many subsequent studies have followed this formula

- Ingredients: Deep learning + high quality database of ~100,000 medical images + transfer learning

- Many medical imaging tasks in radiology, pathology, dermatology, and opthamology can be fully automated in a similar manner

- Similar results emerging from non-image data

How will this technology change medical practice, reimbursement, and other policies?

AUTOMATIC X-RAY READING

https://arxiv.org/pdf/1711.05225.pdf

SUMMARY & CONCLUSIONS

CONCLUSIONS

  • Deep learning models are like legos, but you need to know what blocks you have and how they fit together
  • Could potentially impact many fields -> understand concepts so you have deep learning "insurance"
  • Impact of medical imaging seems inevitable
  • Prereqs: Data (lots) + GPUs (more = better)

Additional Resources

 http://beamandrew.github.io

Made with Slides.com