排序, 枚舉, greedy, 二分搜

8/24 暑假資讀[4]

becaido

講師介紹

建國中學陳柏凱
OJ handle：becaido
經歷：2021 北市賽佳作
　　　2022 TOI 1!
　　　資訊燒雞

因為想學習基本演算法所以當基本演算法講師

演算法?!

>> 演算法（英語：algorithm），在數學（算學）和電腦科學之中，指一個被定義好的、計算機可施行其指示的有限步驟或次序，常用於計算、數據處理和自動推理。演算法是有效方法，包含一系列定義清晰的指令，並可於有限的時間及空間內清楚的表述出來。 --- by Wiki

簡單來說，對於一個特定種類的問題，對於任何符合條件的輸入，我們都能使用一個固定的方法去解決它，並在有限時間輸出。

來舉個例子

給你一個正整數 \(n\)，請你計算 \(1 + 2 + \dots + n\)

輸入：\(n\)

↓

(演算法)

↓

輸出：加總後的結果

我們可以用一個從 \(1 \sim n\) 的 for 迴圈
來加總出想要的東西

int main() {
    // 輸入
    int n;
    cin >> n;
    
    // 執行演算法
    int sum = 0;
    for (int i = 1; i <= n; i++) sum += i;
    
    // 輸出
    cout << sum << '\n';
}

這樣我們就設計出了一個時間複雜度 \(O(n)\) 的演算法！

也就是說，我們寫的程式也能叫做演算法！(通常)

這個程式有什麼缺點?

C++ 中的 int 只能存 \(-2^{31}\sim 2^{31}-1\)

一個演算法應該要不管給定數字的大小，都能在特定的複雜度內求出結果，但受限於電腦硬體的限制，我們實際寫出的演算法往往只能處理特定大小的輸入，於是我們有時也必須優化時間與空間複雜度。

優化 1：程式在 \(n \geq 65536\) 時就會溢位，於是將 int 改成 long long

int main() {
    int n;
    cin >> n;
    
    long long sum = 0; // long long 可以存下 -2^63 ~ 2^63 - 1 的數字
    for (int i = 1; i <= n; i++) sum += i;
    
    cout << sum << '\n';
}

有沒有更快的方法？

有方法優化嗎？(給你們 5 秒想)

在寫一道題目時，我們能想到簡單但是複雜度差的演算法，或許可以拿到部分分

但是若要拿到更多分，我們必須想出複雜度更好，也就是不會 TLE 或是 MLE 的演算法

優化2：相信大家都知道最後的結果可以化簡成 \(\frac{n\times (1 + n)}{2}\)
可以 \(O(1)\) 算出來

int main() {
    int n;
    cin >> n;
    
    long long sum;
    sum = 1ll * n * (n + 1) / 2; // 1ll 是要將型別轉換成 long long

    cout << sum << '\n';
}

題目有給 \(n\) 的範圍嗎？沒有。

這樣要怎麼知道它會不會給一個很大的數字

一個好的題目應該要把輸入的範圍、條件詳細列出來，這樣才能設計出適合的演算法。

剛剛那題，若要使 int 存得下 \(n\)，題目就應該標明 \(1 \leq n < 2^{31}\)。

額外延伸：\(1 \leq n < 2^{63}\) 怎麼做

大數乘法

2. 邪惡黑魔法 __int128

__int128

但有時候必須要用到(之後不知會不會講到那裡)，這時可以自己寫輸入輸出。

優點：可以存 \(-2^{127}\sim 2^{127}-1\) 的數字

缺點：運算速度慢、無法用 cin, cout 輸入輸出、
　　　有些地方無法編譯。

好到不真實(試試你的編譯器能不能編譯這個程式)

#include <bits/stdc++.h> // 萬用標頭檔
using namespace std;

void out (__int128 x) {
    char s[49];
    int len = 0;
    do {
        s[++len] = x % 10 + '0';
        x /= 10;
    } while (x);
    for (int i = len; i >= 1; i--) cout << s[i];
    cout << '\n';
}

int main() {
    long long n;
    cin >> n;
    
    __int128 ans;
    ans = (__int128) n * (n + 1) / 2;

    out (ans);
}

排序

sort

例題：給你一個長度為 \(n \leq 1000\) 的陣列 \(a_1 \sim a_n (-10^9 \leq a_i \leq 10^9)\)，請你把這個陣列由小到大排好並輸出。

要如何排序呢？先想想看如何找最小值。

想法：每次找出數列最小值，把它放到最前面，在繼續找剩下數字的最小值，直到全部排好。

Code：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1005;

int n;
int a[SIZE];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    for (int i = 1; i <= n; i++) {
        int mn = a[i], pos = i;
        for (int j = i; j <= n; j++) {
            if (a[j] < mn) {
                mn = a[j];
                pos = j;
            }
        }
        swap (a[i], a[pos]);
    }

    for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n]; // i == n 時輸出 '\n'，否則輸出 ' '
}

每次找最小值要 \(O(n)\)，要找 \(n\) 次，時間複雜度 \(O(n^2)\)。

例題：給你一個長度為 \(n \leq 10^5\) 的陣列 \(a_1 \sim a_n (-100 \leq a_i \leq 100)\)，請你把這個陣列由小到大排好並輸出。

原本的 \(O(n^2)\) 似乎不行了，注意到 \(a_i\) 的範圍，似乎有可以利用的地方？

假設遇到 \(a_i\)，那我們就把 \(cnt_{a_i}\) 加一，因為 C++ 的下標不能是負數，我們就把每個數字都加 \(100\)，輸出時減 \(100\) 就可以。

Code：

#include <bits/stdc++.h>
using namespace std;

const int MAX = 200;

int n;
int cnt[MAX + 5];

int main() {
    cin >> n;
    while (n--) {
        int x;
        cin >> x;
        cnt[x + 100]++;
    }

    for (int i = 0; i <= 200; i++) {
        while (cnt[i]--) {
            cout << i - 100 << ' ';
        }
    }
    cout << '\n';
}

時間複雜度 \(O(n + C)\)，\(C\) 為陣列數字的值域。

例題：給你一個長度為 \(n \leq 10^5\) 的陣列 \(a_1 \sim a_n (-10^9 \leq a_i \leq 10^9)\)，請你把這個陣列由小到大排好並輸出。

原本的方法都不行了 \(\text{QQ}\)，有沒有一個函式能幫我們自動排好啊？

在講 C++ 裡的函式之前，我們先來講要如何自己寫一個 \(O(n\times \log(n))\) 的排序。

假設我們有兩個排序好的陣列，要如何將它們合併呢？

那要如何把一個沒排序的陣列變成兩個排序好的小陣列呢？

其實就只要看兩個陣列裡開頭的元素，把比較小的放到前面就可以了。

可以寫一個遞迴函式，將陣列分成兩半遞迴下去，直到陣列長度等於一。排好之後就可以合併了！這個方法稱為 Merge Sort。

每次會把陣列分一半，所以每個數字最多會被計算到 \(\log(n)\) 次，時間複雜度 \(O(n\times \log(n))\)。

Code：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n;
int a[SIZE], tmp[SIZE];

void MergeSort (int l, int r) {
    if (l == r) return;

    // 遞迴計算
    int mid = (l + r) / 2;
    MergeSort (l, mid);
    MergeSort (mid + 1, r);

    // 合併陣列
    int p1 = l, p2 = mid + 1;
    for (int i = l; i <= r; i++) {
        if (p1 > mid) tmp[i] = a[p2++]; // 左邊陣列已用完
        else if (p2 > r) tmp[i] = a[p1++]; // 右邊陣列已用完
        else {
            if (a[p1] <= a[p2]) tmp[i] = a[p1++];
            else tmp[i] = a[p2++];
        }
    }
    for (int i = l; i <= r; i++) a[i] = tmp[i];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    MergeSort (1, n);

    for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n];
}

現在來講 C++ 裡好用的排序函式，
<algorithm> 裡的 sort。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n;
int a[SIZE];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    sort (a + 1, a + n + 1);

    for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n];
}

時間複雜度 \(O(n\times \log(n))\)

平常預設排序的方式是傳入陣列起始位置與終止位置，由小排到大。

如何由大排到小呢？sort 預設的比較方法是 less<>，我們可以把它改成 greater<>

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n;
int a[SIZE];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    sort (a + 1, a + n + 1, greater<int>());

    for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n];
}

也可以對字串按照字典序排大小，vector 也可以！

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n;
string s[SIZE];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> s[i];

    sort (s + 1, s + n + 1);

    for (int i = 1; i <= n; i++) cout << s[i] << '\n';
}

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n;
vector<int> v[SIZE];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int k;
        cin >> k;
        while (k--) {
            int x;
            cin >> x;
            v[i].push_back (x);
        }
    }

    sort (v + 1, v + n + 1);

    for (int i = 1; i <= n; i++) {
        for (int x : v[i]) cout << x << ' ';
        cout << '\n';
    }
}

例題：給你一個長度為 \(n \leq 10^5\) 的陣列 \(a_1 \sim a_n (0 \leq a_i \leq 10^9)\)，請你把這個陣列按照 \(a_i \bmod k\) 由大到小排好並輸出，若兩個數字 \(\bmod\ k\) 一樣，那按照數字大小由小排到大。

似乎只能自己寫比較函式了，我們可以寫一個函式，或是直接用 C++ 中 lambda 的語法。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n, k;
int a[SIZE];

// 自訂比較函式
bool cmp (int x, int y) {
    int mx = x % k, my = y % k;
    if (mx != my) return mx > my;
    return x < y;
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort (a + 1, a + n + 1, cmp);
    for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n];
}

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n, k;
int a[SIZE];

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> a[i];
    
    sort (a + 1, a + n + 1, [] (int x, int y) {
        int mx = x % k, my = y % k;
        return mx != my ? mx > my : x < y;
    });
    
    for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n];
}

例題：有 \(n \leq 10^5\) 個人，每個人有一個英文名字(以小寫字母表示)，和一個年紀。

請對每個人以年紀由大到小排好，若年紀相同，則以名字的字典序由小到大排好。

我們可以把每個人的名字和年紀用一個 struct 存起來，除了可以用剛剛的自訂比較函式，也可以使用運算子重載，自己定義 < 要怎麼比較。

Code：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

struct Person {
    string name;
    int age;
    bool operator < (const Person &x) const { // 運算子重載
        if (age != x.age) return age > x.age;
        return name < x.name;
    }
} p[SIZE];

int n;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> p[i].name >> p[i].age;
    sort (p + 1, p + n + 1);
    for (int i = 1; i <= n; i++) cout << p[i].name << ' ' << p[i].age << '\n';
}

練習：

好多裸題：ZJ a233, TIOJ 1287, TIOJ 1328, TIOJ 1682, ZJ d190, ZJ a104

類裸題：ZJ f277, ZJ e544, ZJ e927, ZJ d550, ZJ a528, ZJ a915, ZJ d750, ZJ a225, TIOJ 1585, ZJ c531, ZJ c635, ZJ c634, ZJ c633, ZJ c630, ZJ a539

ZJ i399 - 1. 數字遊戲 (2022 6月 APCS)

TIOJ 2193 - A. 原始人排序 (2021 TOI pA)

Merge Sort：TIOJ 1080, ZJ d542, ZJ c260

TIOJ 1720 - 餐廳評鑑 (2010 TOI pE)

ZJ h873

枚舉

枚舉也叫做暴力 (brute force)，也就是在解題時窮舉答案，在範圍小的時候很常用，但是其複雜度往往會很高，於是在範圍大的時候往往只能拿到部分分，如何水到部分分就變得很重要。

在枚舉的時候應該要好好想一下自己現在要枚舉的是什麼。

例題：ABC 258 B - Number Box

給你一個 \(N \times N\) 的矩陣，第 \(i\) 行第 \(j\) 列有一個數字 \(A_{i, j}\)，可以選擇一個出發點走 \(N\) 步，方向可以選擇 \(8\) 方位的其中一個，把路上遇到的數字接起來，問可以接到的最大數字。

\(1 \leq N \leq 10\)
\(1 \leq A_{i, j} \leq 9\)

看到 \(N\) 很小，就知道可以枚舉。

我們可以先將每個方位的 \(x\) 移動量與 \(y\) 移動量用陣列存好，之後直接枚舉陣列的下標。

可以枚舉出發點與走的方位，走 \(N\) 步後更新答案。

該枚舉什麼？

Code：

#include <bits/stdc++.h>
using namespace std;

const int dx[8] = {-1, 0, 0, 1, -1, -1, 1, 1};
const int dy[8] = {0, -1, 1, 0, -1, 1, -1, 1};

// 轉換數字，n+1 -> 1，0 -> n
int turn (int num, int n) {
    return num == 0 ? n : num == n + 1 ? 1 : num;
}

int main() {
    int n;
    cin >> n;

    string a[n + 1];
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] = " " + a[i];
    }

    string ans = string (n, '0'); // 初始化答案
    for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) { // 枚舉出發點
        for (int k = 0; k <= 7; k++) { // 枚舉方位
            string s;
            for (int x = i, y = j, cnt = 1; cnt <= n; x = turn (x + dx[k], n), y = turn (y + dy[k], n), cnt++) {
                s += a[x][y];
            }
            ans = max (ans, s); // 更新答案
        }
    }
    cout << ans << '\n';
}

例題：ZJ a010 - 因數分解

給一個數字 n，請你對他質因數分解。

\(2 \leq n \leq 10^8\)

原始的想法：枚舉 \(i = 2\sim n\)，看 \(i\) 是否可以整除 \(n\)，若可以，將 \(n\) 變成 \(\frac{n}{i}\)，繼續看 \(i\) 是否能整除 \(n\) 直到無法整除，換 \(i+1\dots\) 。

或許可以縮小枚舉範圍試試看。

怎麼辦 \(\dots\)

時間複雜度 \(O(n)\)，太慢了！

一個數字 \(n\) 最多會有多少 \(\geq \sqrt{n}\) 的質因數？

一個？現在來證明不會多於一個：

於是我們只要枚舉 \(2\leq i \leq \sqrt{n}\) 就好了，最後若 \(n≠ 1\)，那它就是那一個 \(> \sqrt{n}\) 的質因數。

但是 \(p_1, p_2 \geq \sqrt{n}\)，所以 \(n = k\times p_1^{t_1}\times p_2^{t_2} > n\)，矛盾。

若 \(n\) 有兩個不同質因數 \(p_1, p_2 \geq \sqrt{n}\)，那 \(n\) 可以表示成 \(k\times p_1^{t_1}\times p_2^{t_2}\)，\(t_1, t_2 \geq 1\)

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    bool f = 0; // 之前是否有輸出數字
    for (int i = 2, sq = sqrt (n); i <= sq; i++) { // sqrt (n) 在一開始先計算好，避免大量的 sqrt 運算
        int cnt = 0;
        while (n % i == 0) {
            cnt++;
            n /= i;
        }
        if (cnt > 0) {
            if (f == 0) f = 1;
            else cout << " * ";
            if (cnt == 1) cout << i;
            else cout << i << '^' << cnt;
        }
    }

    if (n > 1) {
        if (f == 1) cout << " * ";
        cout << n;
    }
    cout << '\n';
}

Code：\(O(\sqrt{n})\)

練習題：CSES 1081

枚舉 0/1 狀態

有的時候當題目給的 \(n \leq 20\) 時，我們可以考慮枚舉狀態

於是就可以枚舉 \(i = 0 \sim 2^n - 1\)

什麼是枚舉狀態呢？一個數字以二進位表示會有許多 \(0, 1\)，那就可以把為 0 的位元當作不取這個數字，把為 1 的位元當作要取這個數字。

例題：有 \(n\) 個人，想從他們裡面挑出一些人，假設挑出 \(k\) 人，須滿足 \(L\leq k \leq R\)，第 \(i\) 個人與第 \(j\) 個人若被挑出來，那就會有 \(a_{i, j}\) 的快樂值 \((a_{i, i} = 0, a_{i, j} = a_{j, i})\)，想問快樂值最大可以是多少？

\(1 \leq L \leq R \leq n \leq 20\)
\( -100 \leq a_{i, j} \leq 100\)

想法：可以利用位元枚舉選了哪些人，算出答案後更新。

#include <bits/stdc++.h>
using namespace std;

const int INF = 1e9; // 設定一個極大的數字

int main() {
    int n, L, R;
    cin >> n >> L >> R;

    int a[n][n];
    for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) cin >> a[i][j];

    int ans = -INF;
    for (int i = 0, I = 1 << n; i < I; i++) {
        int cnt = __builtin_popcount (i); // 計算二進制裡有多少 1
        if (cnt < L || cnt > R) continue;
        int sum = 0;
        for (int j = 0; j < n; j++) {
            if ((i >> j & 1) == 0) continue;
            for (int k = j + 1; k < n; k++) {
                if (i >> k & 1) {
                    sum += a[j][k];
                }
            }
        }
        ans = max (ans, sum);
    }
    cout << ans << '\n';
}

Code：\(O(n^2\times 2^n)\)

練習題：CSES 1623, TIOJ 2060, ZJ b002, ZJ f991

枚舉排列(字典序)

有的時候想要把所有可能的排列按照字典序一個一個找出來，除了自己慢慢寫一個遞迴或是迴圈，還可以怎麼枚舉？

利用 <algorithm> 裡的 next_permutation, prev_permutation 就可以了

具體方法就是先把陣列排序好，用一個 do-while 迴圈，等到到了最大字典序後，它的回傳值就會自動使迴圈停止，甚至可以自己寫一個比較函式。假設數列長度是 \(n\)，每個相同的數字有 \(a_i\) 個，那根據排列組合，枚舉的複雜度為 \(O(\frac{n!}{a_1!a_2!\dots a_k!})\)

例題：給你一個長度為 \(n\leq 10\) 的數列 \(a_1\sim a_n (1\leq a_i \leq 9)\)，問你有多少種排列可以使這個排列的數字全部接起來後，是 k 的倍數 \((1 \leq k \leq 7122)\)

Code：\(O(n\times \frac{n!}{\prod(每個數字出現幾次)!})\)

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, k;
    cin >> n >> k;

    int a[n + 1];
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort (a + 1, a + n + 1); // 排序

    int ans = 0;
    do {
        int sum = 0;
        for (int i = 1; i <= n; i++) {
            sum = (10 * sum + a[i]) % k;
        }
        ans += (sum == 0);
    } while (next_permutation (a + 1, a + n + 1)); //

    cout << ans << '\n';
}

練習題：TIOJ 1113, ZJ a524, ZJ d436, ZJ e446, ZJ e942

ZJ c272

例題：CSES 1628 - Meet in the Middle

給你一個長度為 \(n \leq 40\) 的陣列 \(a_1 \sim a_n\)，問有多少個子集合的數字總和為 \(x\)。

可以用剛剛的位元枚舉，但是 \(2^{40}\) 太大了，該怎麼辦呢？

不如我們把陣列分兩半，看看可以做什麼事。

Code：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 20;
const int MAX = 1 << SIZE;

int n, m, x;
int a[SIZE], b[SIZE];
long long ans;
long long A[MAX], B[MAX];

int main() {
    cin >> n >> x;
    m = n / 2, n = n - m; // 將陣列分成兩半
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0; i < m; i++) cin >> b[i];

    for (int i = 0; i < (1 << n); i++) {
        for (int j = 0; j < n; j++) {
            if (i >> j & 1) {
                A[i] += a[j];
            }
        }
    }
    for (int i = 0; i < (1 << m); i++) {
        for (int j = 0; j < m; j++) {
            if (i >> j & 1) {
                B[i] += b[j];
            }
        }
    }

    sort (A, A + (1 << n));
    sort (B, B + (1 << m));

    int sum = 0, pos = (1 << m) - 1; // B 現在跑到哪個位置
    for (int i = 0; i < (1 << n); i++) {
        if (i && A[i] == A[i - 1]) {
            ans += sum;
            continue;
        }
        sum = 0;
        while (pos >= 0 && A[i] + B[pos] > x) pos--;
        while (pos >= 0 && A[i] + B[pos] == x) pos--, sum++;
        ans += sum;
    }
    cout << ans << '\n';
}

我們可以在左邊的陣列裡由小到大看，那如果加總要是 \(x\)，右邊陣列的數字一定會越來越小，我們就可以在 \(O(n\times 2^{\frac{n}{2}})\) 的時間複雜度計算出答案。

分別計算兩邊可以組合出什麼數字，排序了以後，就可以計算有多少可能了。

練習題：CF 525E, CF 1006F

遞迴枚舉

直接上練習題：

TIOJ 1235, TIOJ 1025, ZJ a160, ZJ b510, ZJ h098
CSES 1625

TIOJ 1719 - 商品特賣問題 (2010 TOI pD)

主要就是利用遞迴暴力搜索，有的時候看似極大的複雜度，透過剪枝，也就是對某些特定的情況判斷或是優先挑選比較小的分支去遞迴，那就可以在時限內通過。

greedy

貪心

解決問題時，一直運用某種策略，來得到最好的解。貪心法常常需要被證明，我們在解題時可以通過反證法、數學歸納法或是其他方法(也可以通靈)去證明，這裡會有幾個 greedy 的例子。

例題：ZJ b231 - TOI2009 第三題：書

有 \(n\) 本書需要印刷並裝訂，有 \(n\) 臺裝訂機，但只有一臺印刷機，給每本書印刷、裝訂所需時間，問最快多久可以全部裝訂完。

遇到這題該怎麼辦呢？我們需要找出一種印刷順序使得總時間最短。

如果我們按照裝訂時間由大到小排會是好的嗎？接下來就是證明。

假設現在有兩本書，印刷時間分別為 \(a_1, a_2\)，裝訂時間分別為 \(b_1, b_2\)，\(b_1 < b_2\) 且 \(b_1\) 在前面，假設在 \(a_1\) 前的印刷時間總和為 \(X\)，在 \(a_2\) 前的印刷時間總和為 \(Y\)，那原本的答案為
\(\max(X + a_1 + b_1, Y + a_2 + b_2)\)，

若交換了兩本書，那答案會變成

\(\max(X + a_2 + b_2, Y - a_1 + a_2 + a_1 + b_1)\)
\(X + a_2 + b_2\) 比 \(Y + a_2 + b_2\) 小，\(Y + a_2 + b_1\) 也比 \(Y + a_2 + b_2\) 小，於是我們便證明了把裝訂時間大的放在前面肯定會比較好。

Code：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1005;

int n, ans;
pair<int, int> p[SIZE];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> p[i].first >> p[i].second;
    sort (p + 1, p + n + 1, [] (pair<int, int> p1, pair<int, int> p2) {
        return p1.second > p2.second;
    });
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum += p[i].first;
        ans = max (ans, sum + p[i].second);
    }
    cout << ans << '\n';
}

例題：TIOJ 1861 - 蘿莉切割問題

有 \(n\) 個人，每個人想要長度為 \(a_i\) 的木頭，你有一個長度為 \(L = \sum\limits_{i = 1}^{n}a_i\) 的木頭，將長度為 \(x\) 的木頭切成兩塊時要花 \(x\) 單位的力氣，問最後將木頭全部切完後最少需要花的力氣。

這要如何 greedy 呢？不妨把問題變成把 \(a_1 \sim a_n\) 一直合併變成 \(L\)。

我們如果合併最小的兩個木頭會是好的嗎？

假設現在有三根木頭 \(a_1\leq a_2\leq a_3\)，那有三種合併方法，最後需要花的力氣分別為 \(2a_1+2a_2+a_3, 2a_1+a_2+2_a3, a_1+2a_2+2a_3\)，而最小的正是第一種合併方法，先將最小的兩個合併。

類似題：ABC 252 F

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio (false), cin.tie (0); // 輸入輸出優化
    int n;
    while (cin >> n) {
        priority_queue<int, vector<int>, greater<int>> pq; // min_heap
        long long ans = 0;
        while (n--) {
            int x;
            cin >> x;
            pq.push (x);
        }
        while (pq.size() >= 2) {
            int a, b;
            a = pq.top(), pq.pop();
            b = pq.top(), pq.pop();
            ans += a + b;
            pq.push (a + b);
        }
        cout << ans << '\n';
    }
}

於是我們可以用一個 priority_queue，每次挑最小的兩個合併。

Code：

練習題：ZJ c471, ZJ d418, ZJ f005, ZJ h927, TIOJ 1072, TIOJ 1440,
TIOJ 1441, TIOJ 2009, TIOJ 1030, ARC 135 A,
TIOJ 1788, TIOJ 1976, TIOJ 2266, CSES 2426, TIOJ 2220

二分搜

binary search

在講二分搜之前，好像都會先玩一個遊戲。

請你想一個策略，使得不管我想的數字是多少，都能使詢問的次數最小化。

現在我心裡想了一個數字 \(n(1\leq n \leq 10000)\)，每次你可以猜一個數字 \(x\)，我會回答你 \(x\leq n\) 或是 \(x > n\)。

假設現在答案可能的區間為 \([l, r]\)，我們猜了一個數字 \(x\)，那答案可能的區間會變成什麼？

我們可以一個一個猜，但是這樣太慢了！

如果 \(x \leq n\)，那區間會從 \([l, r]\) 變成 \([x, r]\)；

如果 \(x > n\)，那區間會從 \([l, r]\) 變成 \([l, x - 1]\)。

知道了這個以後，要如何選擇 \(x\) 呢？

每次選了 \(x\) 之後，會讓原本的區間分成兩半，但我們不知道會到大的區間還是小的區間。

於是我們讓兩個區間的大小盡量接近，這樣不管區間變怎樣都會至少縮小一半。

這樣查詢的次數就是 \(O(\log(n))\)，YA!

實作細節

我們知道要把區間變成一半了，那 \(x\) 具體要設多少呢？

哪一個是對的？(r = mid - 1, l = mid)

#include <bits/stdc++.h>
using namespace std;

int n; // the answer

bool bigger (int x) {
    cout << "guess " << x << '\n';
    return x > n;
}

int main() {
    cout << "the answer is ";
    cin >> n;
    cout << "you have to guess it\n";

    int l = 1, r = 10000;
    while (l < r) {
        cout << "before guess : [l, r] = " << "[" << l << ", " << r << "]\n";
        int mid = (l + r) / 2;
        if (bigger (mid)) r = mid - 1;
        else l = mid;
        cout << "after guess :  [l, r] = " << "[" << l << ", " << r << "]\n\n";
    }
    cout << "answer is " << l << '\n';
}

#include <bits/stdc++.h>
using namespace std;

int n; // the answer

bool bigger (int x) {
    cout << "guess " << x << '\n';
    return x > n;
}

int main() {
    cout << "the answer is ";
    cin >> n;
    cout << "you have to guess it\n";

    int l = 1, r = 10000;
    while (l < r) {
        cout << "before guess : [l, r] = " << "[" << l << ", " << r << "]\n";
        int mid = (l + r) / 2 + 1;
        if (bigger (mid)) r = mid - 1;
        else l = mid;
        cout << "after guess :  [l, r] = " << "[" << l << ", " << r << "]\n\n";
    }
    cout << "answer is " << l << '\n';
}

mid = (l + r) / 2

mid = (l + r) / 2 + 1

假設答案是 \(2217\)

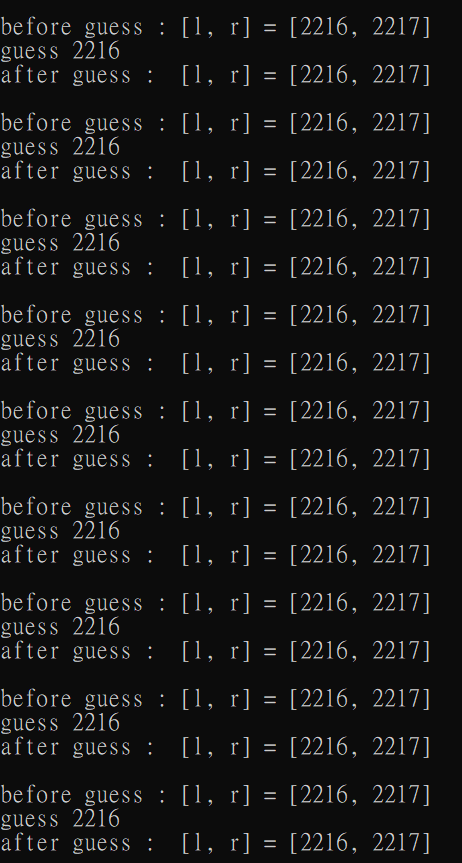
第一個程式：

卡住了...

第二個程式：

成功猜出

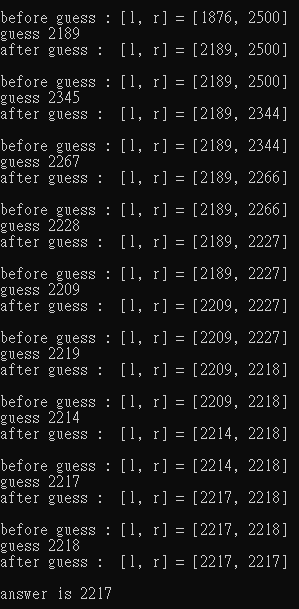
為什麼會這樣 \(\text{QQ}\)？

注意到第一個程式卡在了 \([2216, 2217]\)，每次會猜 \((2216 + 2217) / 2 = 2216\)，而 \(2216\leq n = 2217\)，所以把 \(l\) 設成 \(2216\)，無限迴圈...

我們可以知道在 r = mid - 1, l = mid 的情況，將 mid 設成 (l + r) / 2 + 1 會比較好

遊戲規則稍加改變，每次會回答你 \(x<n\) 或是 \(x\geq n\)。

如果 \(x<n\)，區間會從 \([l, r]\) 變成 \([x + 1, r]\)；

如果 \(x\geq n\)，區間會從 \([l, r]\) 變成 \([l, x]\)。

於是這次會變成 r = mid, l = mid + 1

哪一個是對的？(r = mid, l = mid + 1)

#include <bits/stdc++.h>
using namespace std;

int n; // the answer

bool bigger (int x) {
    cout << "guess " << x << '\n';
    return x >= n;
}

int main() {
    cout << "the answer is ";
    cin >> n;
    cout << "you have to guess it\n";

    int l = 1, r = 10000;
    while (l < r) {
        cout << "before guess : [l, r] = " << "[" << l << ", " << r << "]\n";
        int mid = (l + r) / 2;
        if (bigger (mid)) r = mid;
        else l = mid + 1;
        cout << "after guess :  [l, r] = " << "[" << l << ", " << r << "]\n\n";
    }
    cout << "answer is " << l << '\n';
}

mid = (l + r) / 2

mid = (l + r) / 2 + 1

#include <bits/stdc++.h>
using namespace std;

int n; // the answer

bool bigger (int x) {
    cout << "guess " << x << '\n';
    return x >= n;
}

int main() {
    cout << "the answer is ";
    cin >> n;
    cout << "you have to guess it\n";

    int l = 1, r = 10000;
    while (l < r) {
        cout << "before guess : [l, r] = " << "[" << l << ", " << r << "]\n";
        int mid = (l + r) / 2 + 1;
        if (bigger (mid)) r = mid;
        else l = mid + 1;
        cout << "after guess :  [l, r] = " << "[" << l << ", " << r << "]\n\n";
    }
    cout << "answer is " << l << '\n';
}

把答案換成 \(7122\)

第一個程式：

成功猜出

第二個程式：

卡住了...

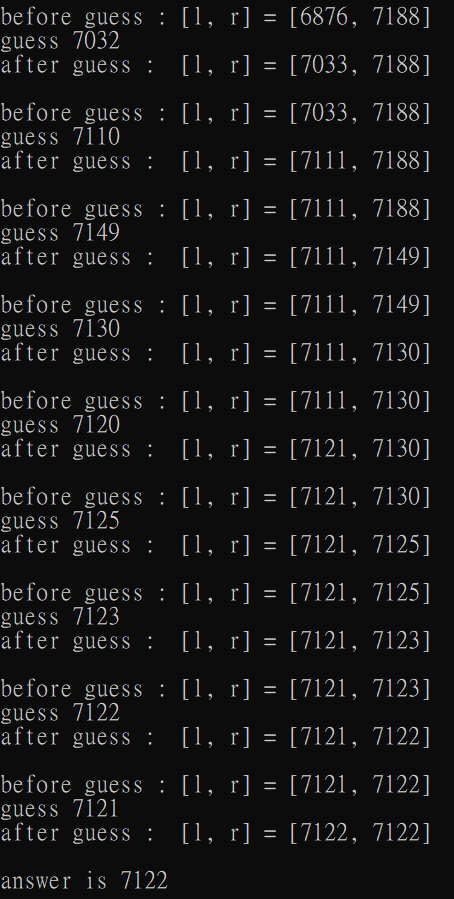
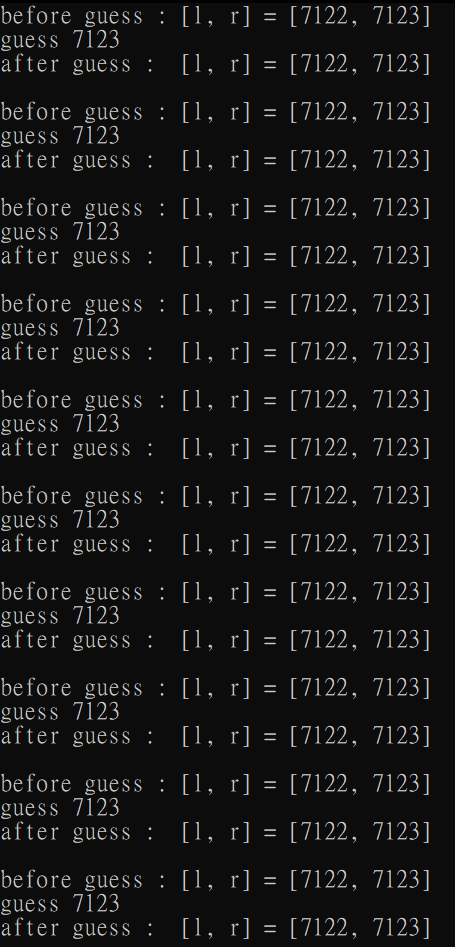
第二個程式卡在了 \([7122, 7123]\)，每次會猜
\((7122 + 7123) / 2 + 1 = 7123\)，而 \(7123\geq n = 7122\)，所以把 \(r\) 設成 \(7123\)，無限迴圈...

我們可以知道在 r = mid, l = mid + 1 的情況，將 mid 設成 (l + r) / 2 會比較好

那除了把方法背下來，或是把數字代進去看看會不會一直無限迴圈，有沒有什麼取 mid 的小訣竅？

就是當 l, r 裡有一個是 mid + 1 時，那就將 mid 設成 (l + r) / 2；

就是當 l, r 裡有一個是 mid - 1 時，那就將 mid 設成 (l + r) / 2 + 1。

(一個互補的概念)

反正如果你二分搜時一直卡住，那你就改改看取 mid 的方式，看看會不會比較好。

l, r 可能是負數

可以把 (l + r) / 2 變成 l + (r - l) / 2，變成正數後再進行除法的運算。

遇到什麼題目該用二分搜呢？

題目問你最大(小)的答案是多少，假設最大答案為 \(x\)，那代表 \(\leq x\) 的都能符合題目條件，\(>x\) 的都無法滿足條件。

例題：CF 1610 C - Keshi Is Throwing a Party

Waimai 有 \(n\) 個朋友，第 \(i\) 個朋友有 \(i\) 塊錢，若第 \(i\) 個朋友被 Waimai 邀請到派對，那派對裡最多只能有 \(a_i\) 人比他富有，最多只能有 \(b_i\) 人比他窮。

問最多可以邀請幾人？

假設最多可邀 \(x\) 人，那邀 \(1\sim x - 1\) 人可以嗎？

答案是可以的，因為人變少，比較富有的或比較窮的也會變比較少。

於是我們可以二分搜總共要邀請幾人。假設邀請了 \(x\) 人，那就去判斷可不可以。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 2e5 + 5;

int n;
int a[SIZE], b[SIZE];

// 判斷是否可以 x 人
bool ok (int x) {
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        if (b[i] >= cnt && a[i] >= x - cnt - 1) {
            cnt++;
        }
        if (cnt == x) return 1;
    }
    return 0;
}

void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];

    int l = 1, r = n;
    // 二分搜
    while (l < r) {
        int mid = (l + r) / 2 + 1;
        if (ok (mid)) l = mid;
        else r = mid - 1;
    }
    cout << l << '\n';
}

int main() {
    int tt;
    cin >> tt;
    while (tt--) solve();
}

Code：\(O(n\times\log(n))\)

例題：ZJ h084 - 4. 牆上海報 (2022 1月 APCS)

有 \(n\) 個寬度 \(1\)、高度 \(h_i\) 的木板，有 \(k\) 個海報，寬度為 \(w_1\sim w_k\)，高度為 \(1\)，想把它們都放在同一個高度，而且有木板地方才能放，問最高可以放的高度。

觀察：高度越高，可以放的空間只能越來越少，所以假設最高可放的高度是 \(x\)，那比 \(x\) 低的一定也可以。

Code：\(O(n\times \log(C))\)(\(C\) 為最大高度)

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 2e5 + 5;
const int KSIZ = 5005;
const int INF = 1e9;

int n, k;
int h[SIZE], w[KSIZ];

bool ok (int x) {
    int pos = 1, len = 0;
    for (int i = 1; i <= n; i++) {
        if (h[i] >= x) len++;
        else len = 0;
        if (len == w[pos]) {
            pos++;
            len = 0;
        }
        if (pos > k) return 1;
    }
    return 0;
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> h[i];
    for (int i = 1; i <= k; i++) cin >> w[i];

    int l = 1, r = INF;
    while (l < r) {
        int mid = (l + r) / 2 + 1;
        if (ok (mid)) l = mid;
        else r = mid - 1;
    }
    cout << l << '\n';
}

所以我們可以對高度二分搜，看當前的高度是否能放好海報。

例題：給你一個長度為 \(n\leq 10^5\) 的陣列，有 \(Q \leq 10^5\) 筆詢問，每次給你一個整數 \(x\)，請輸出陣列裡 \(\geq x\) 且最接近 \(x\) 的數字，若無，輸出 \(\text{ACorz}\)。

想法：先把陣列排序好，然後可以進行剛剛的二分搜。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n, q;
int a[SIZE];

int main() {
    cin >> n >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort (a + 1, a + n + 1);

    while (q--) {
        int x;
        cin >> x;
        if (x > a[n]) {
            cout << "ACorz\n"; // ACorz
            continue;
        }
        int l = 1, r = n;
        while (l < r) {
            int mid = (l + r) / 2;
            if (a[mid] >= x) r = mid;
            else l = mid + 1;
        }
        cout << a[l] << '\n';
    }
}

Code：

有沒有更簡短的作法呢？

lower_bound 會回傳第一個 \(\geq x\) 數字的位置，

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n, q;
int a[SIZE];

int main() {
    cin >> n >> q;
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort (a + 1, a + n + 1);

    while (q--) {
        int x;
        cin >> x;
        int pos = lower_bound (a + 1, a + n + 1, x) - a; // lower_bound 回傳的是指標，所以要扣掉陣列開頭的 a
        if (pos > n) cout << "ACorz\n";
        else cout << a[pos] << '\n';
    }
}

Code：

可以利用 <algorithm> 裡的 lower_bound 跟 upper_bound

upper_bound 會回傳第一個 \(> x\) 數字的位置。

例題：ZJ i401：3. 雷射測試 (2022 6月 APCS)

注意到 \(x, y\) 的範圍，我們可以直接開 \(60000\) 個 \(\text{vector}\)，並運用剛剛的 lower_bound。

Code：

#include <bits/stdc++.h>
using namespace std;

const int MAX = 6e4 + 5;

int n, ans;
vector<pair<int, int>> vx[MAX], vy[MAX];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int t, x, y;
        cin >> x >> y >> t;
        y += 30000;
        vx[x].emplace_back (y, t);
        vy[y].emplace_back (x, t);
    }
    vx[0].emplace_back (30000, 0);
    vy[30000].emplace_back (0, 0);
    for (int i = 0; i <= 60000; i++) {
        if (vx[i].size() >= 2) sort (vx[i].begin(), vx[i].end());
        if (vy[i].size() >= 2) sort (vy[i].begin(), vy[i].end());
    }
    int x = 0, y = 30000, d = 1;
    while (1) {
        if (d == 1) {
            int px = lower_bound (vy[y].begin(), vy[y].end(), make_pair (x, -1)) - vy[y].begin();
            if (px + 1 == vy[y].size()) break;
            x = vy[y][px + 1].first;
            if (vy[y][px + 1].second == 0) d = 2;
            else d = 4;
        } else if (d == 2) {
            int py = lower_bound (vx[x].begin(), vx[x].end(), make_pair (y, -1)) - vx[x].begin();
            if (py + 1 == vx[x].size()) break;
            y = vx[x][py + 1].first;
            if (vx[x][py + 1].second == 0) d = 1;
            else d = 3;
        } else if (d == 3) {
            int px = lower_bound (vy[y].begin(), vy[y].end(), make_pair (x, -1)) - vy[y].begin();
            if (px == 0) break;
            x = vy[y][px - 1].first;
            if (vy[y][px - 1].second == 0) d = 4;
            else d = 2;
        } else {
            int py = lower_bound (vx[x].begin(), vx[x].end(), make_pair (y, -1)) - vx[x].begin();
            if (py == 0) break;
            y = vx[x][py - 1].first;
            if (vx[x][py - 1].second == 0) d = 3;
            else d = 1;
        }
        ans++;
    }
    cout << ans << '\n';
}

進階題：OJDL 7156 - 雷射測試 2.0
同樣也是二分搜

對斜率(變化量)二分搜

例題：ZJ f990 - 距離

平面上有 \(n\leq 10^5\) 個點，有一條直線 \(y = mx + k\)，請你在直線上找出一點，使其與 \(n\) 個點的距離和最小。

把圖形畫出來看看長怎樣。

假設直線為 \(y = -x + 5\)，有 \(4 \) 個點 \((1, 3), (-2, 5), (3, -4), (2, 8)\)，那距離就是 \(\sqrt{(x - x_i)^2+(y - y_i)^2} = \sqrt{(x - x_i)^2 + (-x+5-y_i)^2}\)，把圖形畫出來看看。

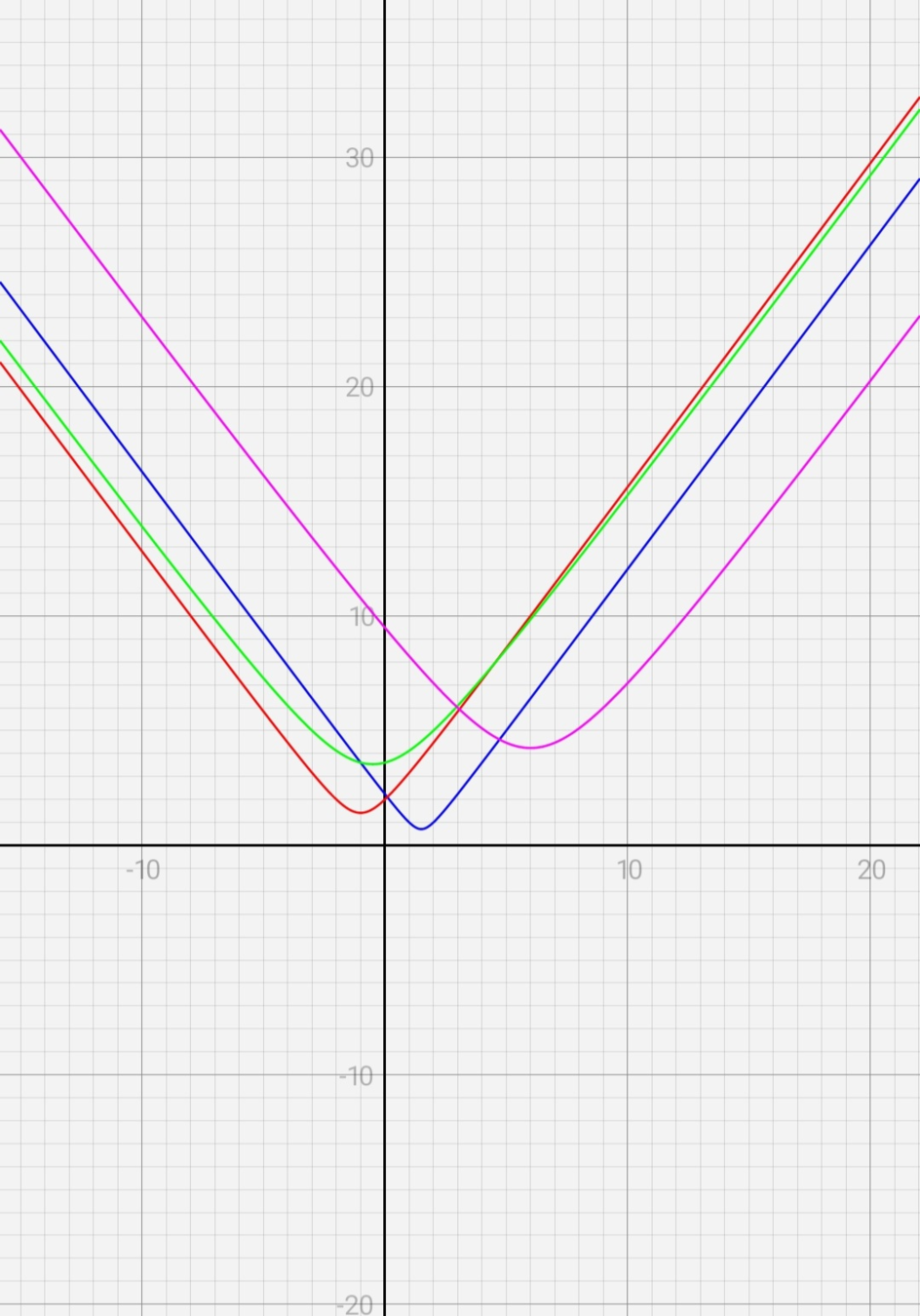
似乎都是凸函數，那把他們相加會怎樣？

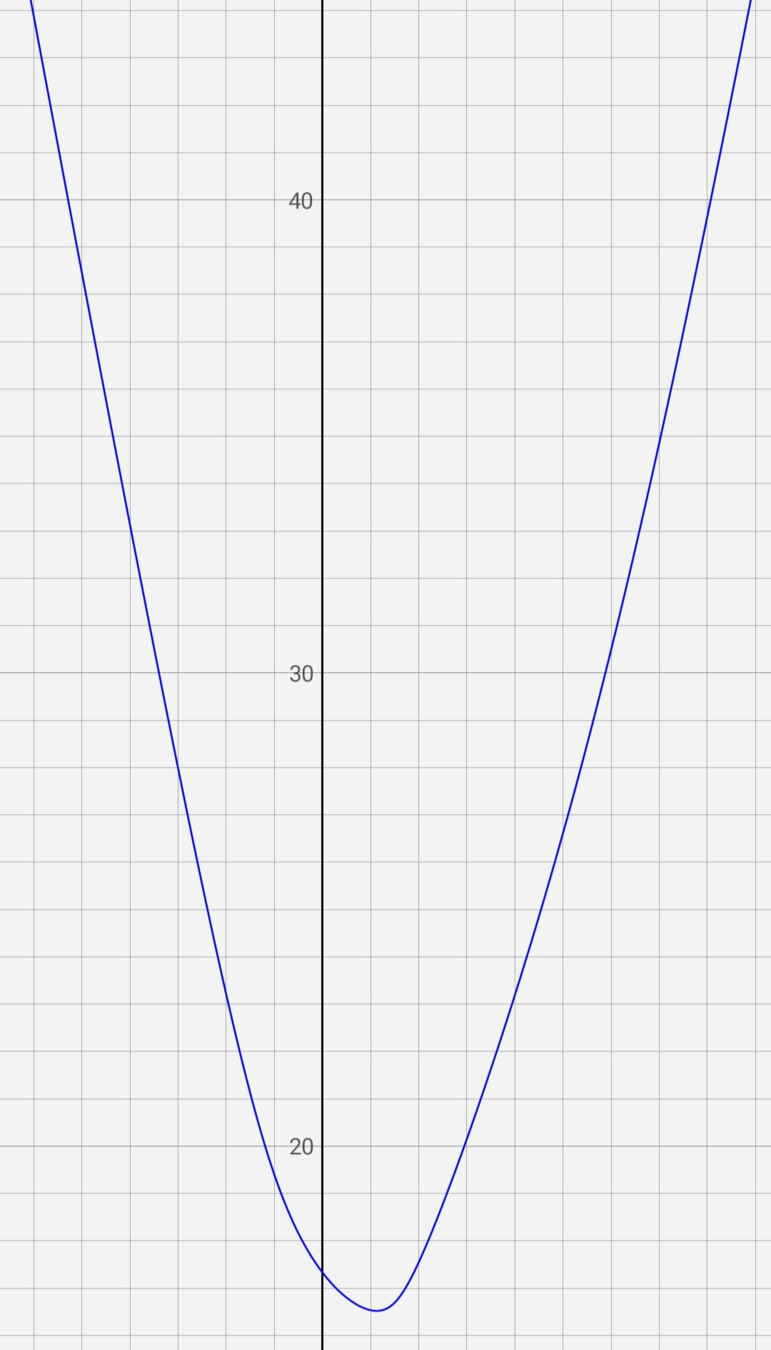
凸函數加凸函數還是一個凸函數

要怎麼二分搜？每次找兩個相近的點 \(x_1, x_2(x_1<x_2)\)，若 \(f(x_1) > f(x_2)\)，那答案應該在右側，否則在左側。

其實對斜率二分搜不限於凹凸函數，只要先遞減(增)後遞增(減)的都可以找到它的極值，運用的就是在極值左側和右側的增減性不同。

小數點的二分搜的方法有兩種，一種是搜到 \(l, r\) 的差距小於某個值時停止，一種是搜了特定次數後停止，以下是以兩種搜尋方式解剛剛那題

Code：差距小於某值

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;
const double MAX = 2e6;
const double eps = 1e-5;
const double delta = 1e-7;

int n, m, k;
int x[SIZE], y[SIZE];

double cal (double X) {
    double Y = m * X + k, sum = 0;
    for (int i = 1; i <= n; i++) sum += sqrt ((X - x[i]) * (X - x[i]) + (Y - y[i]) * (Y - y[i]));
    return sum;
}

void solve() {
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];

    double l = -MAX, r = MAX;
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (cal (mid) < cal (mid + delta)) r = mid;
        else l = mid + delta;
    }
    cout << fixed << setprecision (10) << l << '\n';
}

int main() {
    ios::sync_with_stdio (false), cin.tie (0);
    int tt;
    cin >> tt;
    while (tt--) solve();
}

Code：固定搜尋次數

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;
const int times = 50;
const double MAX = 2e6;
const double delta = 1e-7;

int n, m, k;
int x[SIZE], y[SIZE];

double cal (double X) {
    double Y = m * X + k, sum = 0;
    for (int i = 1; i <= n; i++) sum += sqrt ((X - x[i]) * (X - x[i]) + (Y - y[i]) * (Y - y[i]));
    return sum;
}

void solve() {
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];

    double l = -MAX, r = MAX;
    for (int t = 1; t <= times; t++) {
        double mid = (l + r) / 2;
        if (cal (mid) < cal (mid + delta)) r = mid;
        else l = mid + delta;
    }
    cout << fixed << setprecision (10) << l << '\n';
}

int main() {
    ios::sync_with_stdio (false), cin.tie (0);
    int tt;
    cin >> tt;
    while (tt--) solve();
}

其實還有一種跟斜率二分搜很像的技巧叫「三分搜」，礙於篇幅，就不細講，有興趣的同學可以去搜尋看看。

練習題：ZJ g875, ZJ b844, ZJ f029, ZJ f679, ZJ f815, ZJ f993
ZJ c575 - APCS 2017-0304-4基地台
 ZJ f581 - 3. 圓環出口 (2020 7月 APCS)
TIOJ 1337, TIOJ 1406, TIOJ 1635, TIOJ 1926, TIOJ 2184

TIOJ 2210, TIOJ 2240, CSES 1640, CSES 1641, CSES 1642

CF 1712D

TIOJ 2258 - H. 天竺鼠遊行 (2021 全國賽)
TIOJ 2194 - B. 掃地機器人 (2021 TOI)

TIOJ 1341 - [IOI 2007, Day 1] Aliens

TIOJ 1839 - [IOI 2013] 洞穴 Cave

補充

接下來會講常常用到的技巧

前綴和

前綴和的妙用

例題：給你一個長度 \(n\leq 10^5\) 的數列 \(a_1\sim a_n(|a_i| \leq 10^9)\)，有 \(q \leq 10^5\) 筆詢問，每次給你 \(l, r\) 問你 \(a_l + a_{l + 1} + \dots + a_r\)？

如果每次一個一個加，最後會是 \(O(n\times q)\) ，這樣無法通過，怎麼辦？

我們定義 \(pre_i = a_1 + \dots + a_i = \sum\limits_{j = 1}^i a_j, pre_0 = 0\)，

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n, q;
long long pre[SIZE];

int main() {
    cin >> n >> q;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        pre[i] = pre[i - 1] + x;
    }
    while (q--) {
        int l, r;
        cin >> l >> r;
        cout << pre[r] - pre[l - 1] << '\n';
    }
}

於是我們可以 \(O(n + q)\) 算出來了！

用 \(pre_r\) 減掉 \(pre_{l - 1}\) 就可以了！

那要如何用 \(pre\) 表示 \(\sum\limits_{j = l}^ra_j\)？

例題：(二維版本)給你一個 \(n\times n(n\leq 1000)\) 的二維陣列，第 \(i\) 行第 \(j\) 列的數字為 \(a_{i, j}(|a_{i,j}|\leq 10^9)\)，有 \(q\leq 10^5\) 筆詢問，給你 \(u, l, d, r\)，請你輸出 \(a_{u, l}\) 到 \(a_{d, r}\) 子矩陣的總和。

這次我們讓 \(pre_{i, j}\) 代表 \(\sum\limits_{k_1 = 1}^i\sum\limits_{k_2 = 1}^j a_{k_1, k_2}\)，

Code：\(O(n^2+q)\)

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1005;

int n, q;
long long pre[SIZE][SIZE];

int main() {
    cin >> n >> q;
    for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) {
        int x;
        cin >> x;
        pre[i][j] = x + pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1];
    }
    while (q--) {
        int u, l, d, r;
        cin >> u >> l >> d >> r;
        cout << pre[d][r] - pre[u - 1][r] - pre[d][l - 1] + pre[u - 1][l - 1] << '\n';
    }
}

那我們用 \(pre_{d, r}\) 扣掉 \(pre_{d, l - 1}, pre_{u - 1, r}\) 後，還要加上重複扣的部分 \(pre_{u - 1, l - 1}\)，這就是我們要的答案。

前綴和的妙用：最大連續子區間和

例題：給你一個長度為 \(n\leq 10^5\) 的陣列 \(a_1\sim a_n(|a_i|\leq 10^9)\)，請你求出個陣列裡連續元素和的最大值。

假設現在到了 \(i\)，\(pre_i\) 是固定的，那我們想要讓 \(pre_{l - 1}\) 最小，於是可以維護一個 \(mn\)。

大功告成！

我們可以把 \(a_l+a_{l+1}+\dots +a_r\) 變成 \(pre_r - pre_{l - 1}\)。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1005;
const long long INF = 1e18;

int n;
long long ans = -INF, sum, mn;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        sum += x;
        ans = max (ans, sum - mn);
        mn = min (mn, sum);
    }
    cout << ans << '\n';
}

這樣就可以去解 ZJ i402 - 4. 內積 (2022 6月 APCS) 了！

例題：ZJ b690 - 3. 棕櫚森林

給你長度為 \(n\leq 10^6\) 的陣列 \(a_1\sim a_n\)，問你有多少 \(l, r\) 使得區間 \([l, r]\) 的平均值為 \(\frac{P}{Q}\)。

我們可以先做轉換，把 \(a_i\) 變成 \(Q\times a_i - P\)，這樣就相當於求幾個區間區間和為 \(0\)。

#include <bits/stdc++.h>
using namespace std;

int n, p, q;
long long ans, sum;
unordered_map<long long, int> cnt;

int main() {
    ios::sync_with_stdio (false), cin.tie (0);
    cin >> n >> p >> q;
    sum = -p;
    cnt[sum]++;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        sum += 1ll * x * q - p;
        ans += cnt[sum];
        cnt[sum]++;
    }
    cout << ans << '\n';
}

而這又可以轉換成 \(pre_r - pre_{l-1} = 0, pre_{l - 1} = pre_r\)

我們用一個 unordered_map 即可。

例題：TIOJ 2162 - 辣椒頭大會

給 \(n\leq 2\times 10^5\) 個辣椒，每個辣椒有 \(a_i\) 與 \(b_i\)，假設你吃了區間 \([l, r]\) 的辣椒，會獲得的分數是 \(\frac{\sum\limits_{i=l}^ r a_i}{\sum\limits_{i=l}^ r b_i}\)，且規定要吃超過 \(L\) 個辣椒，問最大分數。

提示：令 \(\frac{\sum\limits_{i=l}^ r a_i}{\sum\limits_{i=l}^ r b_i} = x\)

當 \(\frac{\sum\limits_{i=l}^ r a_i}{\sum\limits_{i=l}^ r b_i} \geq x\) 時，\(\sum\limits_{i=l}^ r a_i \geq x\sum\limits_{i=l}^ r b_i\)，

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 2e5 + 5;
const int times = 50;
const double INF = 1e5;

int n, L;
int a[SIZE], b[SIZE];
double mn[SIZE];

bool ok (double x) {
    double sum = 0;
    for (int i = 1; i <= n; i++) {
        sum += a[i] - x * b[i];
        mn[i] = min (mn[i - 1], sum);
        if (i >= L && sum >= mn[i - L]) return 1;
    }
    return 0;
}

int main() {
    ios::sync_with_stdio (false), cin.tie (0);
    cin >> n >> L;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i];
    double l = 0, r = INF;
    for (int t = 1; t <= times; t++) {
        double mid = (l + r) / 2;
        if (ok (mid)) l = mid;
        else r = mid;
    }
    cout << fixed << setprecision (15) << l << '\n';
}

\(\sum\limits_{i = l}^r (a_i - xb_i) \geq 0\)，所以我們可以對 \(x\) 二分搜，然後找到所有長度 \(\geq L\) 的連續區間和的最大值，看它是否 \(\geq 0\)，就能得知答案！

練習題：前綴和常常搭配其他的算法使用，所以純前綴合的題目也不多。

ZJ e170, CSES 1646, TIOJ 2063

差分

差分的妙用

例題：ZJ e340 - 差分練習

令差分陣列 \(d_i = a_i - a_{i - 1}\)，給你 \(a_1\sim a_n\)，請你求 \(d_1\sim d_n\)。

其實就直接做就好了，會講這題是因為差分陣列可以用在許多地方。

例題：給你一個長度為 \(n \leq 10^5\) 的陣列 \(a\)，初始值皆為 \(0\)，有 \(q\leq 10^5\) 筆操作，每筆操作有 \(l, r, x(|x|\leq 10^9)\)，代表將 \(a_l \sim a_r\) 都增加 \(x\)。

最後請你輸出 \(a_1\sim a_n\)。

每次操作，差分陣列會發生什麼事：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

int n, q;
long long d[SIZE];

int main() {
    ios::sync_with_stdio (false), cin.tie (0);
    cin >> n >> q;
    while (q--) {
        int l, r, x;
        cin >> l >> r >> x;
        d[l] += x;
        d[r + 1] -= x;
    }
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum += d[i];
        cout << sum << " \n"[i == n];
    }
}

於是把差分陣列都算好後，最後就能加總推出原陣列了。

\(d_l\) 增加 \(x\)，\(d_{l + 1}\sim d_r\) 不變，\(d_{r + 1}\) 減少 \(x\)。

例題：CF 1700 C - Helping the Nature

給你一個長度為 \(n\leq 2\times 10^5\) 的陣列 \(a(|a_i|\leq 10^9)\)，有三種操作可以做：

1. 將 \(a_1\sim a_i\) 減少 \(1\)

2. 將 \(a_i\sim a_n\) 減少 \(1\)

3. 將 \(a_1\sim a_n\) 增加 \(1\)

問最少要做幾次操作可以使 \(a_1\sim a_n\) 都變成 \(0\)。

我們觀察差分陣列，三種操作後的差分陣列變化如下：

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 2e5 + 5;

int n;
long long d[SIZE];

void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> d[i];
    for (int i = n; i >= 1; i--) d[i] -= d[i - 1];
    long long ans = 0;
    for (int i = 2; i <= n; i++) {
        ans += abs (d[i]);
        if (d[i] < 0) d[1] -= abs (d[i]);
    }
    ans += abs (d[1]);
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio (false), cin.tie (0);
    int tt;
    cin >> tt;
    while (tt--) solve();
}

而把 \(a_1\sim a_n\) 都變成 \(0\) 就相當於把 \(d_1\sim d_n\) 都變成 \(0\)，於是我們可以從 \(d_2\) 掃到 \(d_n\)，若其為正值，執行操作 2. \(|d_i|\) 次；若其為負值，執行操作 1. \(|d_i|\) 次，並把 \(d_1\) 減少 \(|d_i|\)，最後不管 \(d_1\) 是正是負，都可以執行操作 2. 或操作 3. 讓它變成 \(0\)。

1. \(d_1\) 減少 \(1\)，\(d_{i + 1}\) 增加 \(1\)。

2. \(d_i\) 減少 \(1\)。

3. \(d_1\) 增加 \(1\)。

練習：TIOJ 1227

離散化

lisan

例題：有一個長度為 \(n\leq 10^{18}\) 的陣列 \(a\)，初始值皆為 \(0\)，有 \(m\) 筆操作與 \(q\) 筆詢問 \(m, q \leq 10^5\)，每筆操作會有 \(p\) 與 \(x(1\leq p \leq n, |x|\leq 10^9)\)，代表將 \(a_p\) 增加 \(x\)。每筆詢問會給 \(l, r\)，請你回答 \(a_l+a_{l + 1} + \dots + a_r\)。

\(n\) 好大喔，怎麼辦？

有被操作過的格子 \(\leq 10^5\) 個，所以詢問時只要考慮有被操作過的格子就好了，我們不如把格子們排序好，按照他們的大小重新給他們編號，這樣用前綴和就可以了。

每次問 \(l, r\) 時用二分搜找出對應到的新編號，就可以 \(O(\log(n))\) 回答。

運用到 unique 函式，搭配 vector 的 erase，就可以做出一個離散化的陣列。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 1e5 + 5;

long long n;
int m, q;
pair<long long, int> op[SIZE];
vector<long long> lis (1, 0);
long long pre[SIZE];

int main() {
    cin >> n >> m >> q;
    for (int i = 1; i <= m; i++) {
        auto &[p, x] = op[i];
        cin >> p >> x;
        lis.push_back (p);
    }

    sort (lis.begin(), lis.end());
    lis.erase (unique (lis.begin(), lis.end()), lis.end()); // 去除重複的元素
    n = lis.size() - 1;

    for (int i = 1; i <= m; i++) {
        auto [p, x] = op[i];
        p = lower_bound (lis.begin(), lis.end(), p) - lis.begin();
        pre[p] += x;
    }
    for (int i = 1; i <= n; i++) pre[i] += pre[i - 1];

    while (q--) {
        long long l, r;
        cin >> l >> r;
        l = lower_bound (lis.begin(), lis.end(), l) - lis.begin();
        r = upper_bound (lis.begin(), lis.end(), r) - lis.begin() - 1;
        cout << pre[r] - pre[l - 1] << '\n';
    }
}

有很多題都需要用到離散化，原理就是先全部輸入完後再做處理。

如果題目允許離線的話，那就很方便。

雙指針

two pointer

例題：CSES 2428 - Subarray Distinct Values

給一個長度為 \(n\leq 2\times 10^5\) 的陣列 \(a(1\leq a_i \leq 10^9)\)，問你有幾個子區間裡的數字種類不超過 \(k\) 種。

注意它有一個性質，當區間 \([l, r]\) 可以時，\([l, r - 1], [l, r - 2]\dots [l, l]\) 也可以，於是我們只要知道最右邊在哪裡就好了，而 \(l\) 變大時，\(r\) 必定不會變小，所以就可以讓 \(l\) 從 \(1\) 跑到 \(n\)，看 \(r\) 最遠可以延伸到哪裡，這樣就能 \(O(n)\) 做出來，然後因為要搭配 map，所以最後是 \(O(n\times\log(n))\)。

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 2e5 + 5;

int n, k;
int a[SIZE];
long long ans;
int now;
map<int, int> cnt;

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int l = 1, r = 0; l <= n; l++) {
        // 看 r 最遠可以到哪裡
        while (r < n && now + (cnt[a[r + 1]] == 0) <= k) {
            r++;
            now += cnt[a[r]] == 0;
            cnt[a[r]]++;
        }
        ans += r - l + 1;
        // 移除 a[l]
        cnt[a[l]]--;
        now -= cnt[a[l]] == 0;
    }
    cout << ans << '\n';
}

練習題：ZJ b542, TIOJ 2054

謝謝聆聽！