PHC6194 SPATIAL EPIDEMIOLOGY

Geographically Weighted Regression
Hui Hu Ph.D.
Department of Epidemiology
College of Public Health and Health Professions & College of Medicine
March 25, 2020
Geographically Weighted Regression
Lab: GWR
Geographically Weighted Regression
Traditional Regression Models
- If we apply a traditional regression model to spatial data, we usually assume a stationary process
- the same exposure has the same impact on the outcome in all parts of the study region
- The estimated coefficients are constant over space
- assume that the values of β are the same everywhere
y_i=\beta_0+\beta_1x_{1i}+...+\beta_nx_{ni}+\varepsilon_i
Measured Associations Might Vary Spatially
- Sampling variation
- Associations intrinsically different across space
- e.g. differences in attitudes, different political or other contextual effects
- Model misspecification
Geographically Weighted Regression
- To address the issue of spatial non-stationary directly and allow the associations to vary over space
- We can then estimate the values of β by:
- W(i) is a weight matrix specific to location i such that observations nearer to i are given greater weight than observations further away
y_i=\beta_{0(i)}+\beta_{1(i)}x_{1i}+...+\beta_{n(i)}x_{ni}+\varepsilon_i
\beta_{(i)}=(X^TW_{(i)}X)^{-1}X^TW_{(i)}Y
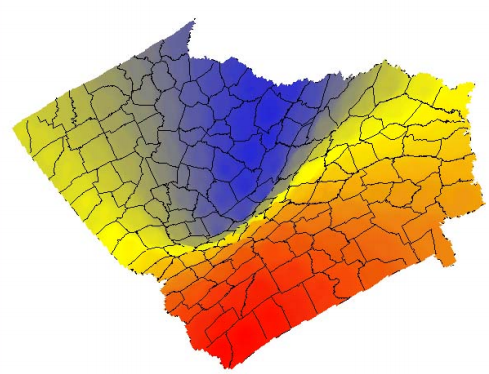
A Typical Spatial Weight Function
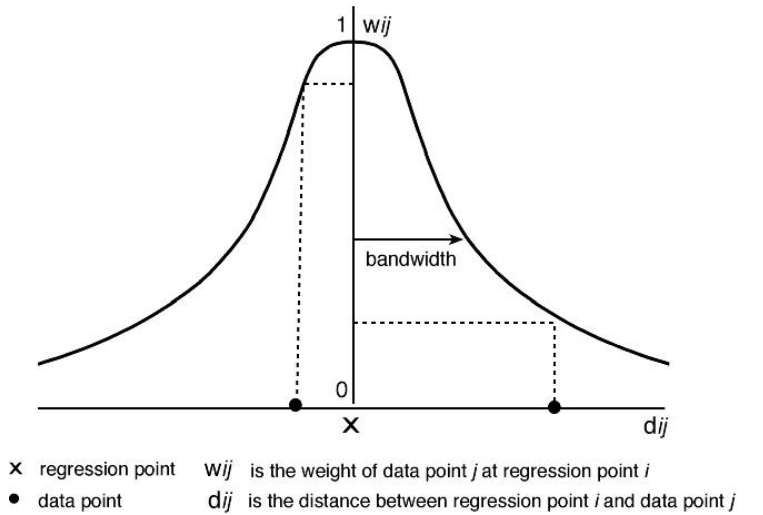
Spatial Weight Functions
- Numerous weight functions can be used
- usually use Gaussian or "Gaussian-like" functions to reflect the type of dependency found in most spatial processes
- can be either fixed or adaptive

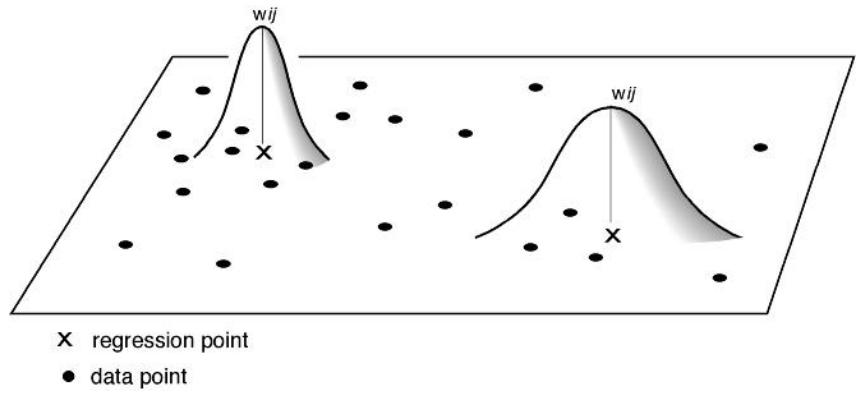
Fixed
Adaptive
W_{ij}=e^{- {{(d_{ij}/h)^2} \over 2}}
h is the bandwidth, as it increases, the gradient of the kernel becomes less steep and more data points are incuded
W_{ij}= \{
[1-(d_{ij}^2/h^2)]^2
0
if j is one of the Nth nearest neighbors of i
otherwise
Calibration
- Results of GWR appear to be relatively insensitive to the choice of weighting functions
- as long as it is a continuous distance-based function
- However, the results will be sensitive to the degree of distance-decay
- Therefore, an optimal value of either h or N has to be obtained
- through minimizing a cross-validated score or the AIC
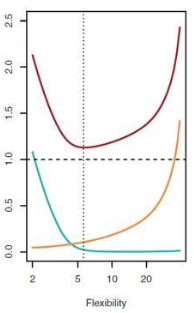
Bandwidth Selection
- Optimal bandwidth selection is a trade-off between bias and variance
- too small a bandwidth leads to large variance in the local estimates
- too large a bandwidth leads to large bias in the local estimates
Output from GWR
- Main output from GWR is a set of location-specific coefficient estimates which can be mapped and analyzed to provide information on spatial non-stationary in associations
- We can also use GWR to
- estimate local standard errors
- derive local t statistics
- calculate local goodness-of-fit measures
- perform tests to assess the significance of the spatial variation in the local parameter estimates
- perform tests to determine if the local model performs better than the global one