Deep Learning
chapter 4
Agenda
- 局部最小值
- 局部最小值對模型的問題
- 鞍點
- 梯度指往錯誤方向
- 以動量為基礎的最佳化作法
- 學習率自動調整
局部最小值
定義
- 求解 lost function 梯度,當梯度為零時,可以說該點是極大 or 極小值。當定義域內的所有極值都求出後,進行比較,除了最小的是全局極小值,其餘都是局部極小值。
- 當維度越多時局部極小值出現的機率也會更小。
局部最小值對模型的問題
學習速率並不好決定
- 過小
- 容易受到局部極小值的影響
- 學習速度過慢
- 過大
- 容易無法收斂

學習率過大
雖然步伐夠大跳出了局部極值,但到全域極值時,因為步伐太大,所以走不到最好的值(無法收斂)

學習濾過小
初始值不好,解就會掉到局部極小值
MBGD
藉由批量更新樣本計算梯度求 lost function 極值的作法。對整個 batch 計算梯度,雖然不會受到極端資料的影響,但是運算量大,資料量大會比較棘手。
容易收斂到局部極小值
SGD
隨機取樣時對每個樣本計算梯度,一次就只進行一次更新,不像BGD計算太多次,但是犧牲準確性,會讓 lost function震盪大。
有機會藉由震盪跳出局部極小值
鞍點

y=x^3
問題
- 小批量梯度遞減在遇到鞍點時很容易會停止,而當模形是多維度的時候,鞍點是很容易遇到的狀況。
想法
- 方向對!盡可能找到更多可能的局部最低點,讓整體得到的值更接近全局最低點。
- 速率快!加快學習率,讓突破鞍點的機會增加。
梯度指往錯誤方向
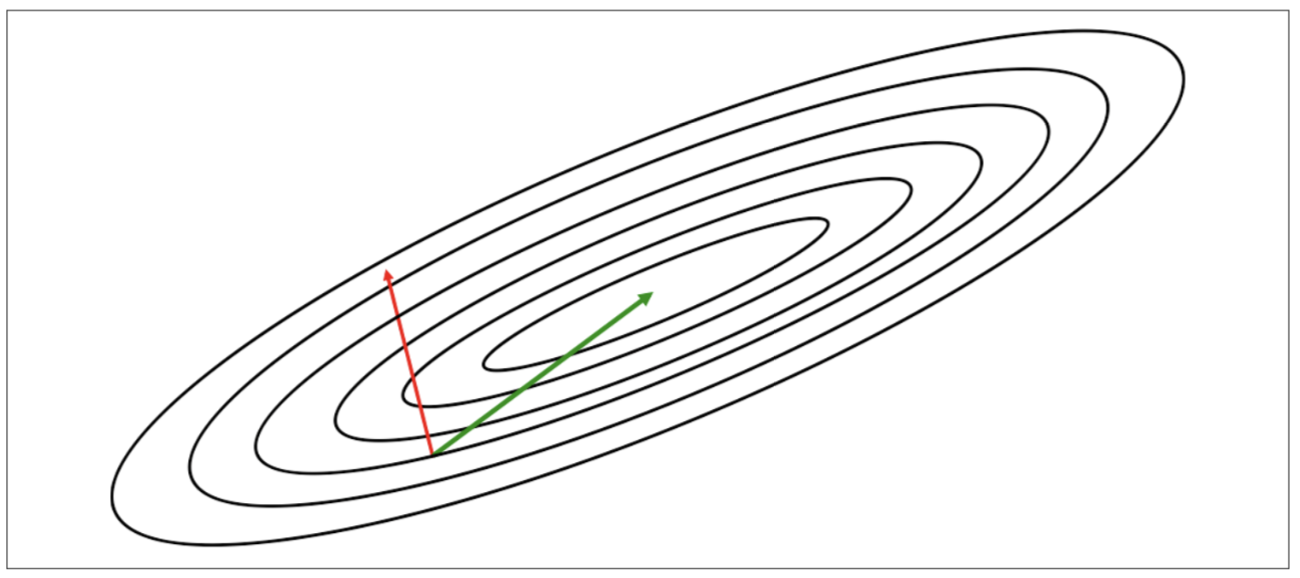
一階導函數的問題
由於梯度是誤差函數對於單一維度的導函數,所以並不能有效指往正確的方向

x
y
z

二階函數
& 海森矩陣


x
y
z
海森矩陣的病態問題
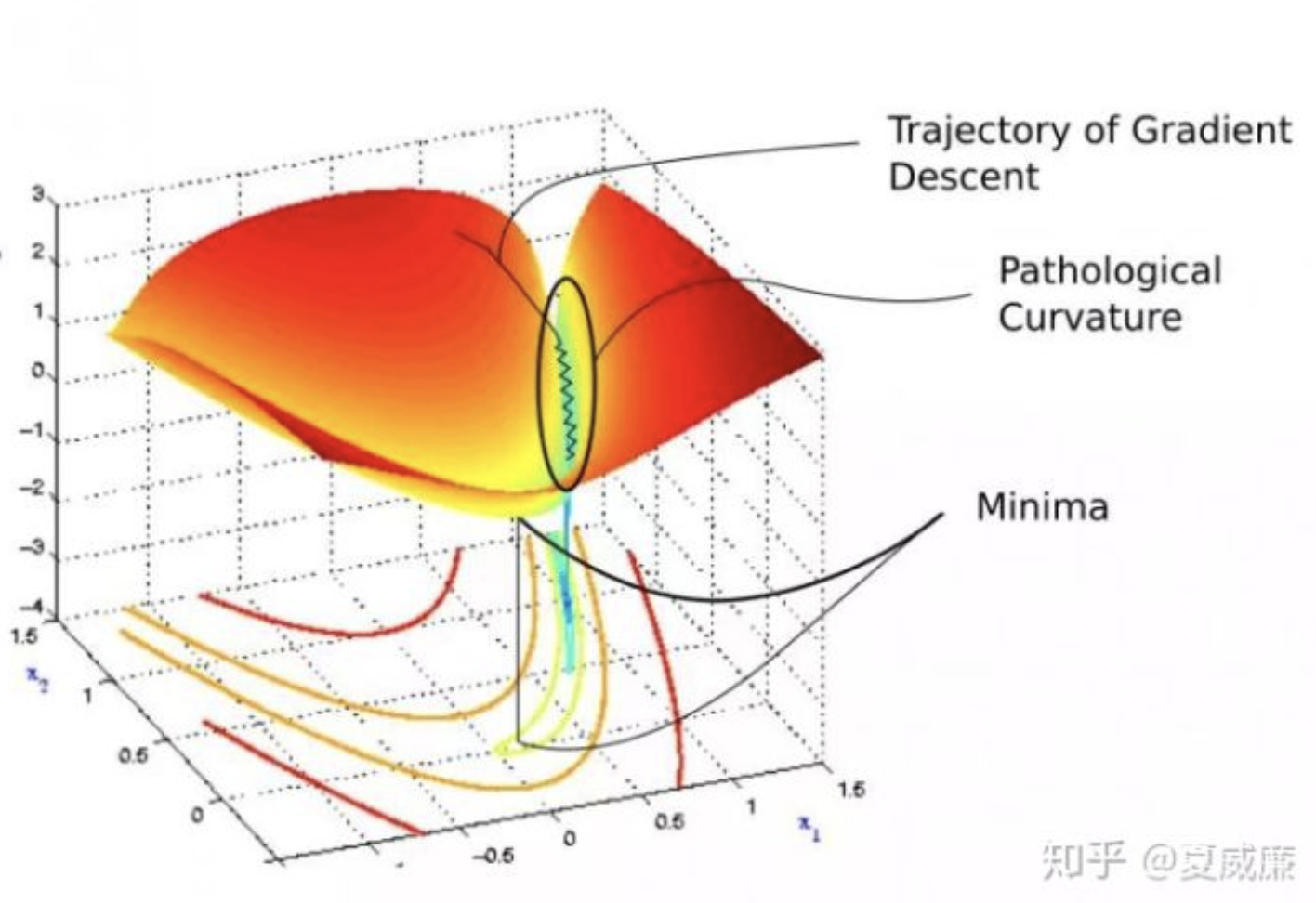

w1方向上的曲率太大了
拖累收斂的行進速度
計算海森矩陣的困難點
耗時耗空間!
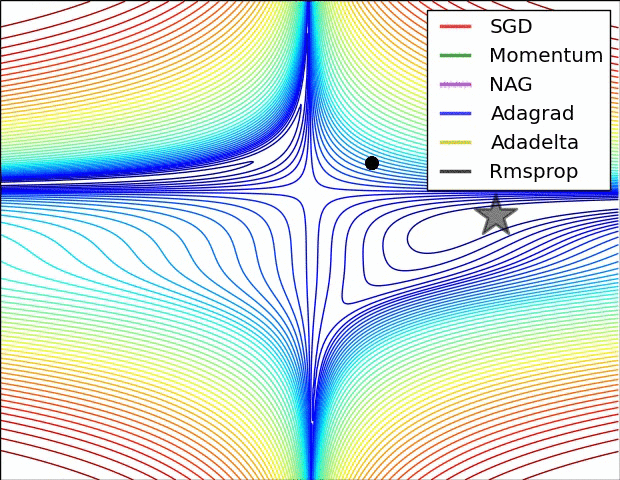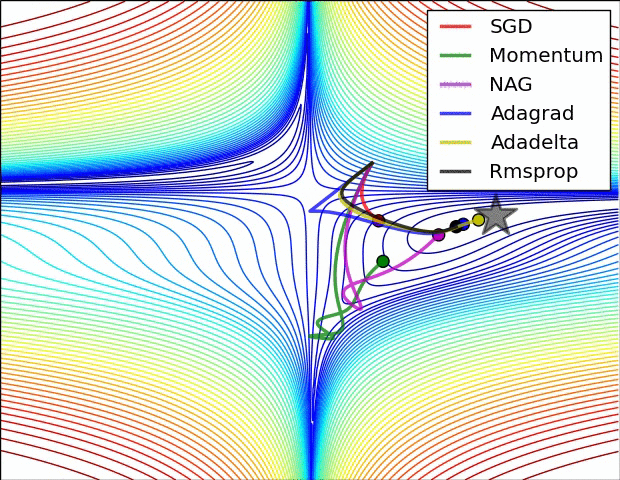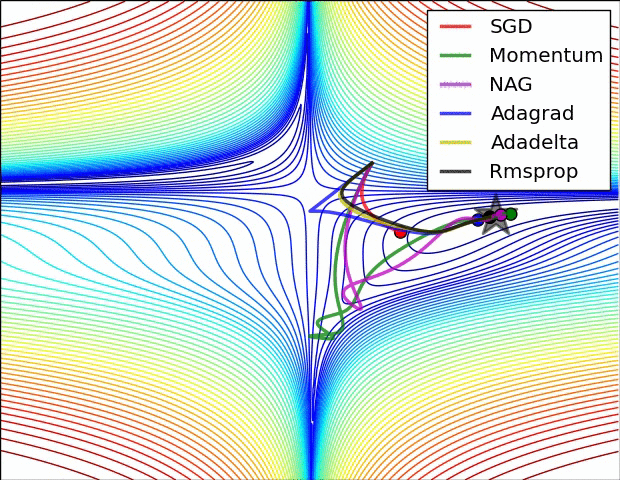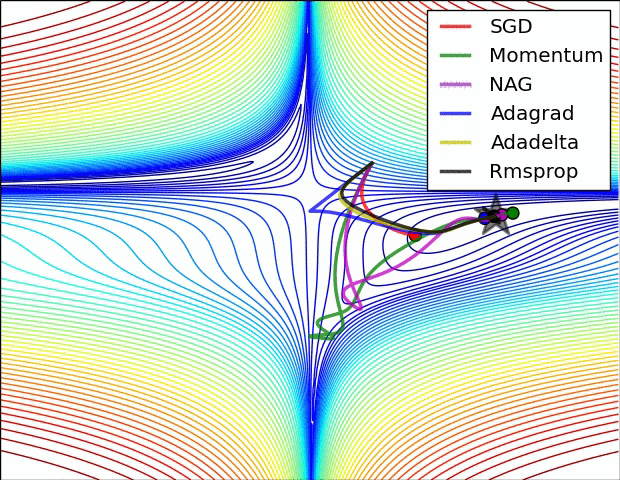
以動量為基礎的最佳化作法
(改善方向,也改善速率)
Main Algorithm
v_i = mv_{i-1} - \epsilon g_i
\theta_i = \theta_{i-1} + v_i
每一次計算更新值的時候,
考慮當下的梯度跟前一次的更新值
- 相較於小批量梯度遞減,可以大幅度加快學習速度
- 初始學習速率需要設定較低,因為動量的特性容易讓學習速率衝很快
- 改善病態曲率的震盪效應
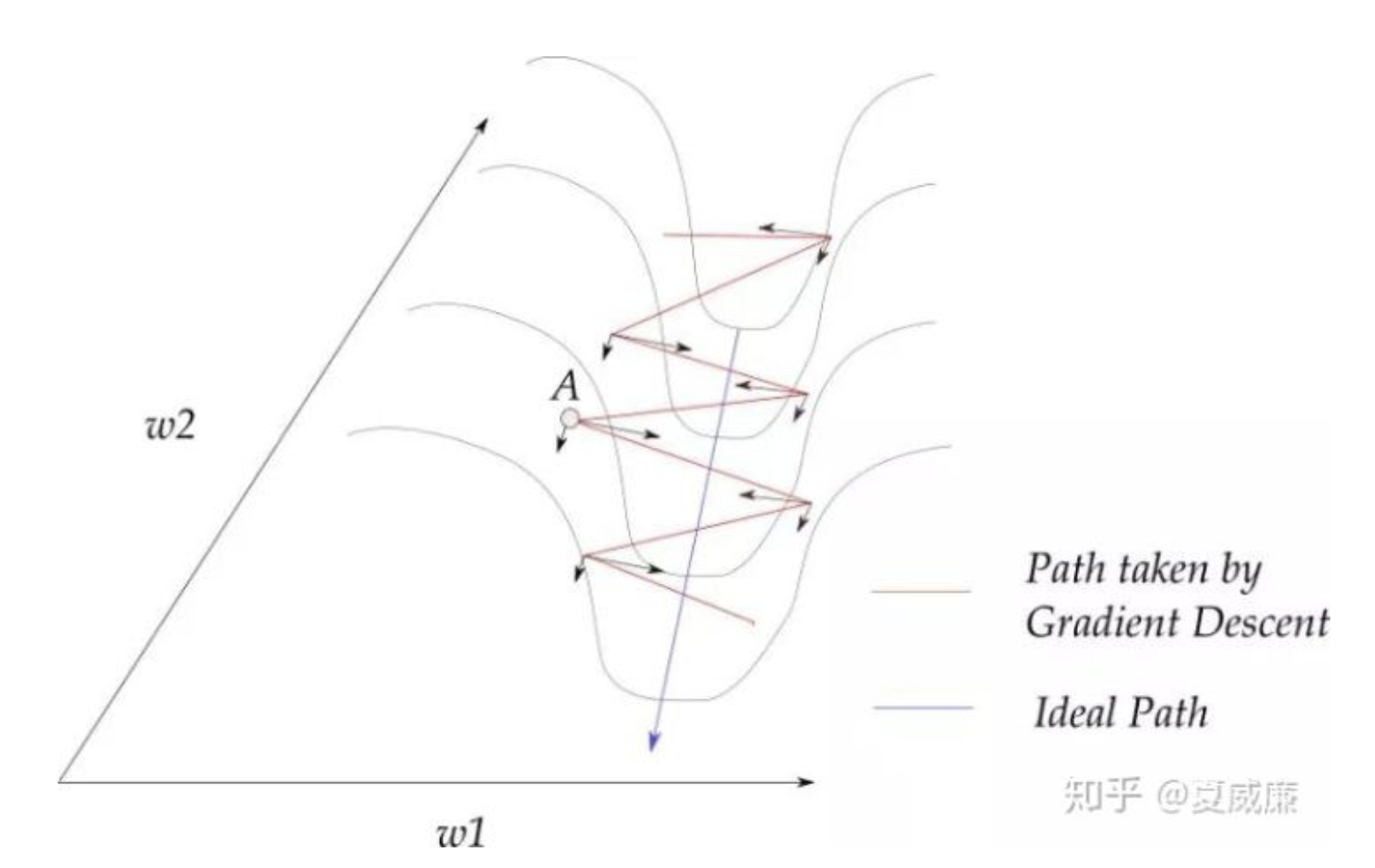
w1分量會相互抵銷,
進而強化往w2方向的移動速率!
學習率自動調整
AdaGrad
依照歷史梯度調整速率
RMSProp
依照平均歷史梯度調整速率
r_i = r_{i-1} + g_i \odot g_i
\theta_i = \theta_{i-1} - \frac {\xi}{\delta \oplus \sqrt {r_i}}\odot g
r_i = \rho r_{i-1} + (1 - \rho) g_i \odot g_i
\theta_i = \theta_{i-1} - \frac {\xi}{\delta \oplus \sqrt {r_i}}\odot g
能有效克服病態曲面
但容易使學習速率下降
解決AdaGrad太早收斂問題
但多了一個超參數增加變因
而且仍然依賴全局學習速率
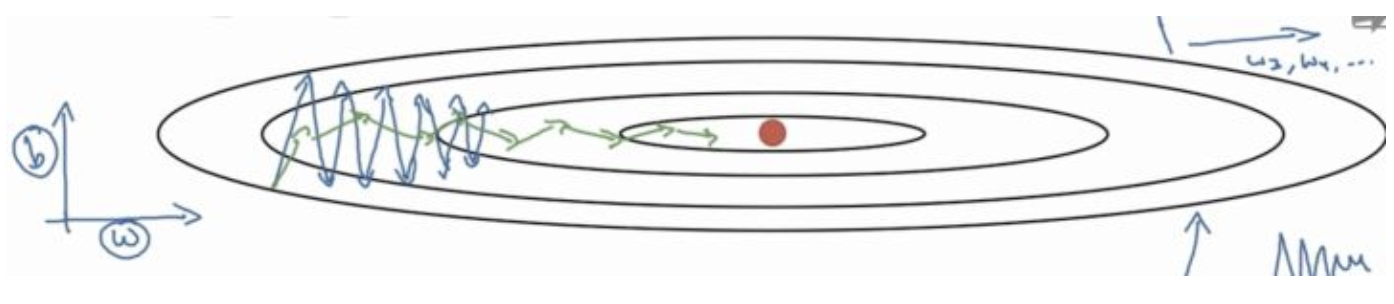
RMSProp
依照平均歷史梯度調整速率
Adam
依照平均歷史梯度&動量調整速率
\theta_i = \theta_{i-1} - \frac {\xi}{\delta \oplus \sqrt {r_i}}\odot g
r_i = \rho r_{i-1} + (1 - \rho) g_i \odot g_i
解決AdaGrad太早收斂問題
但多了一個超參數增加變因
而且仍然依賴全局學習速率
\theta_i = \theta_{i-1} - \frac {\xi}{\delta \oplus \sqrt {v_i}} {m_i}
加入動量之後能夠避免在病態曲率中無謂的震盪
小結
- 大多數的專家對於那一種方式比較好並無共識
- 這些演算法的出現主要是為了更容易訓練
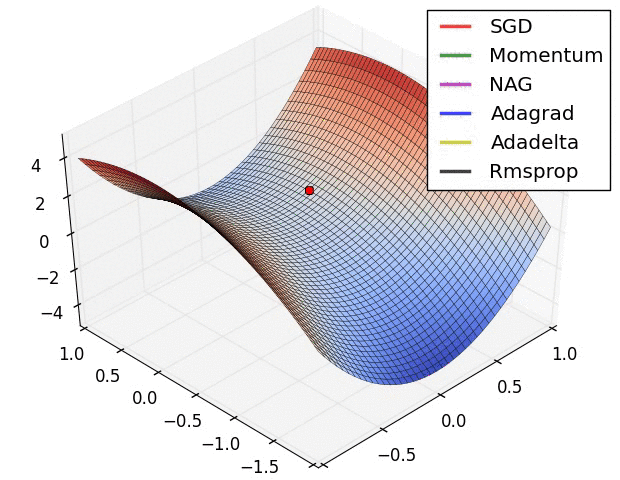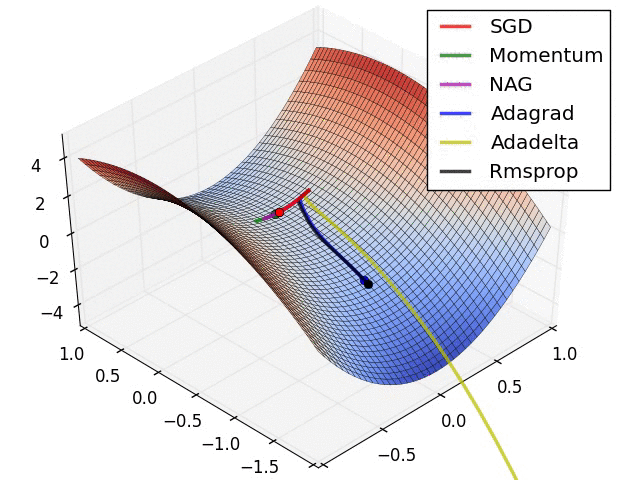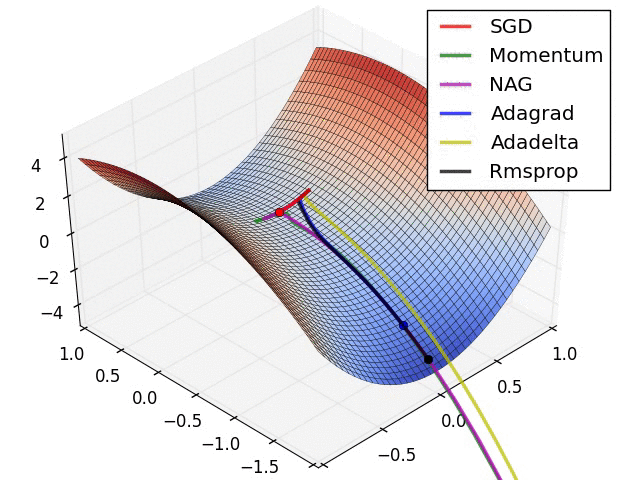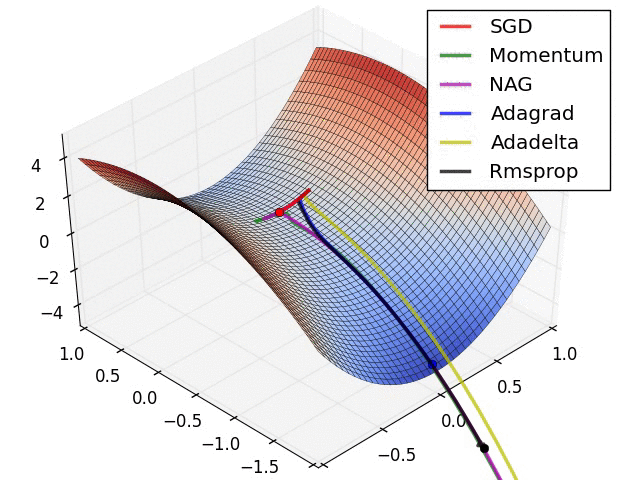

Reference
- https://reurl.cc/GpMbD
- https://zh.wikipedia.org/wiki/%E9%9E%8D%E9%BB%9E
- http://www.csuldw.com/2016/07/10/2016-07-10-saddlepoints/
- https://www.jiqizhixin.com/articles/2018-11-15-23
- https://www.jiqizhixin.com/articles/2018-07-29-6
- https://zhuanlan.zhihu.com/p/29920135
- https://blog.csdn.net/sinat_22336563/article/details/70432297