Starks explained to my grandma

Kindly note that she had a MS in mathematics though

Let's get cooking!

Low degree polynomial extension with its FRIed constraints

Ingredients

a problem to solve
an arithmetization of the problem
some notions about polynomials
having heard about finite fields
~ integers bounded by a prime number
knowing that if \( x_0 \) is a root of a polynomial \(f \), then \( f \) has the form
\( f: x \mapsto (x - x_0) \cdot g(x) \)

Step 1

Have a problem to solve

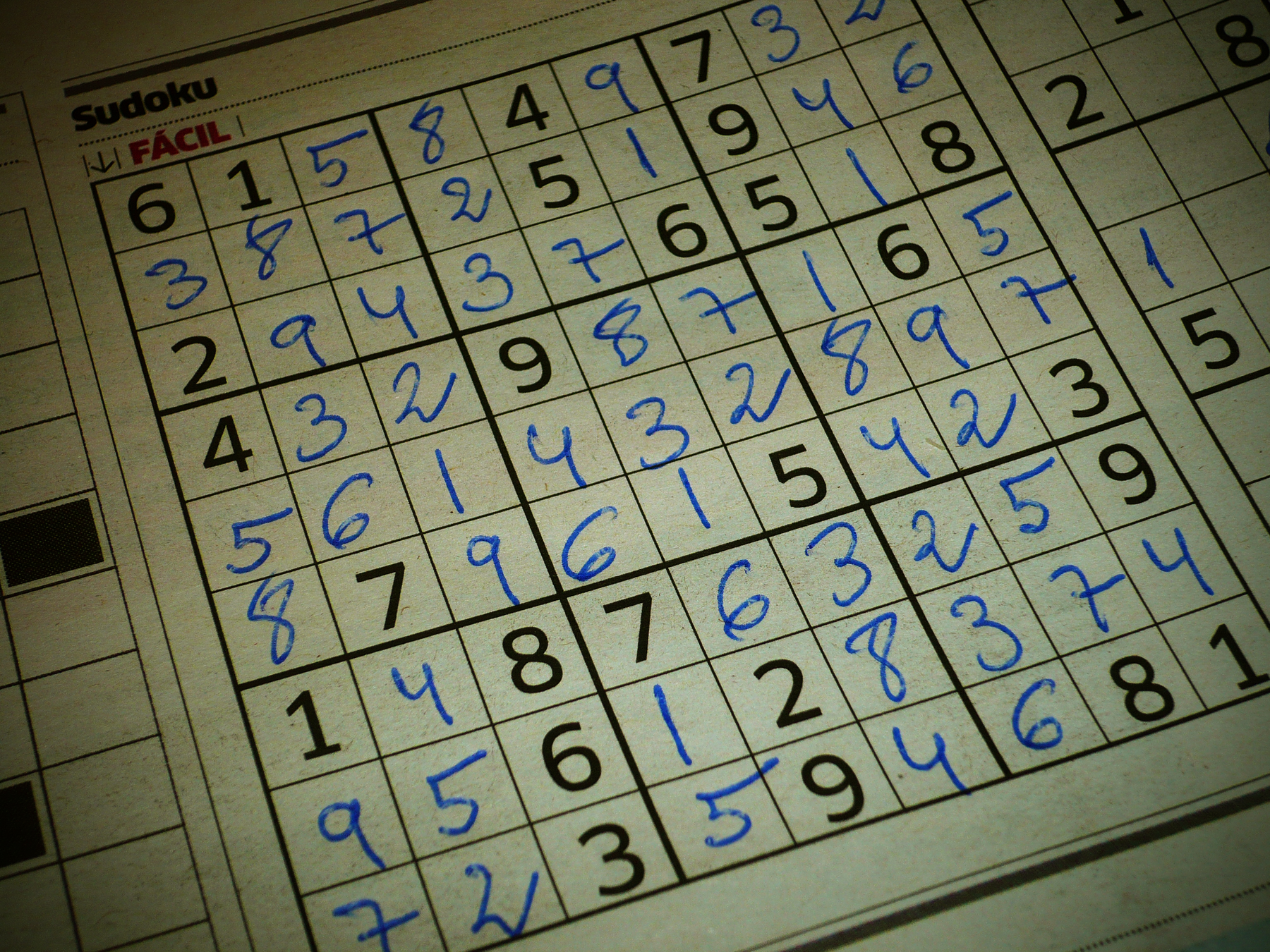
Given an incomplete sudoku grid, I know a valid solution to this grid

Step 2

Arithmetize it

\begin{bmatrix} x_0 & x_1 & \cdots & x_8 \\ x_9 & x_{10} & \cdots & x_{17} \\ \vdots & & \ddots & \vdots \\ x_{72} & x_{73} & \cdots & x_{80} \end{bmatrix}

(x_i - 1) \cdot (x_i - 2) \cdots (x_i - 9) =0 \quad \forall i \in [0, 80]

(x_i - 1) \cdot (x_{i+1} - 1) \cdots (x_{i+8} - 1) \\ + (x_i - 2) \cdot (x_{i+1} - 2) \cdots (x_{i+8} - 2) \\ + \cdots \\ + (x_i - 9) \cdot (x_{i+1} - 9) \cdots (x_{i+8} - 9) \\ =0 \quad \forall i \in {0, 8, \cdots, 72}

All values are in [1,9]

Lines are valid

The Low degree extension sauce

Where the actual Stark journey starts

Choose a special \( g \) value and associate all the Sudoku's \( x_i \) to its exponents

\begin{vmatrix} g^0 & x_0 \\ g^1 & x_1 \\ \cdots \\ g^{80} & x_{80} \end{vmatrix}

Step 1

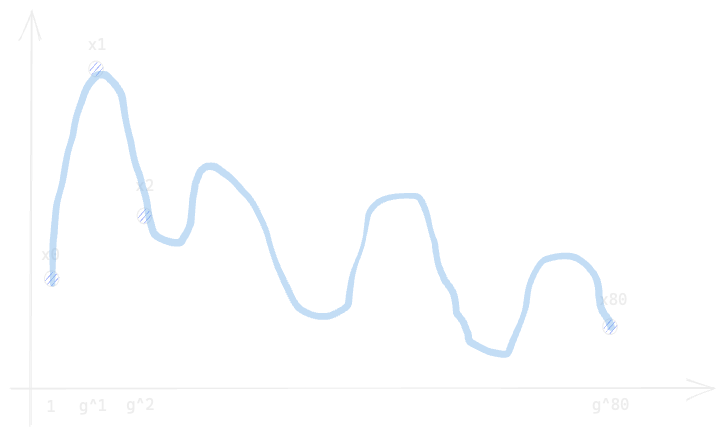
Interpolate a polynomial going through all those points, let's call it \( f \)

Step 2

Then add a shitload of points on the polynomial, say 10 times the original points

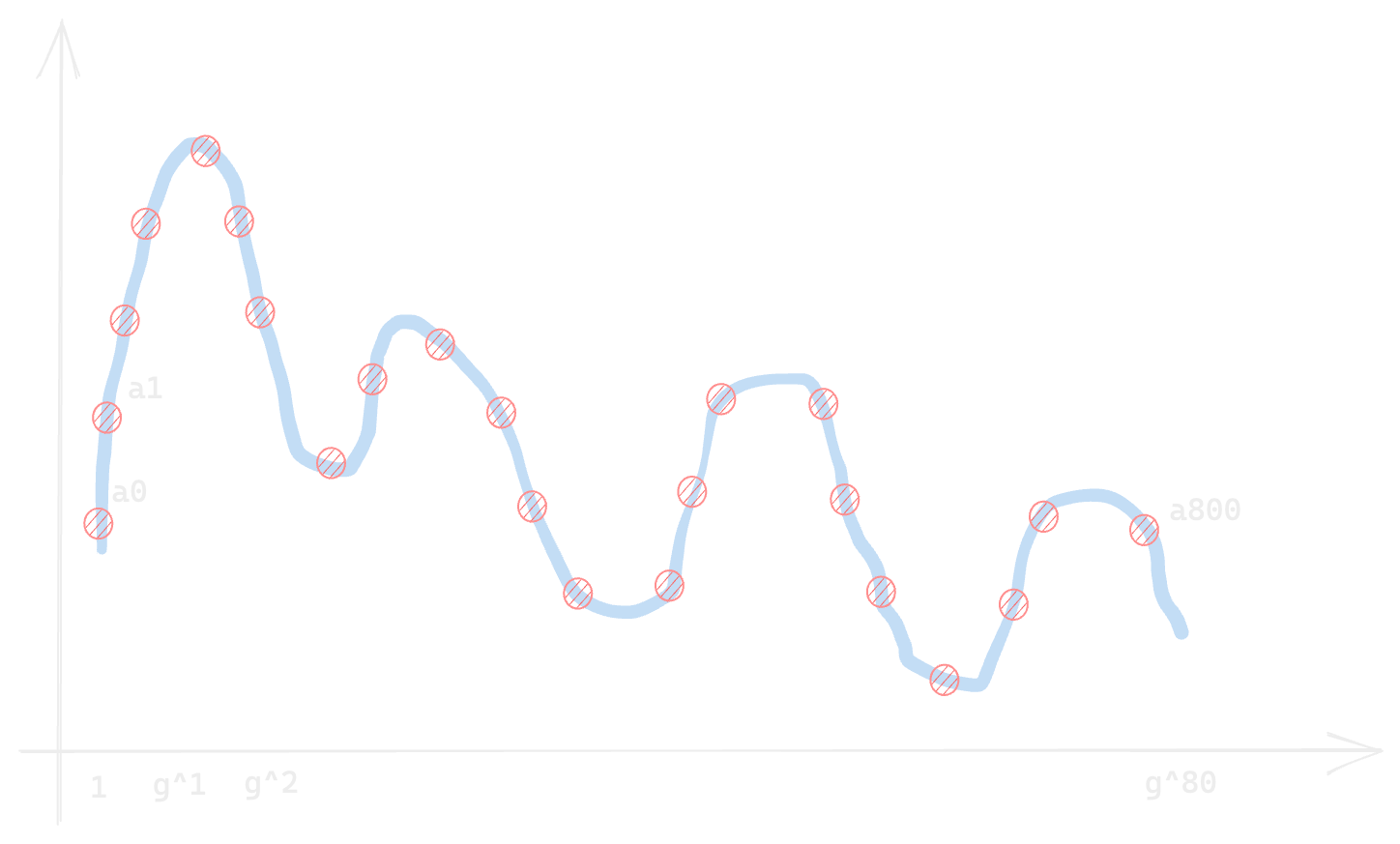
Step 3

Commit these points

Step 4

Prepare the boiled constraints

Transform your problem into polynomial constraints

(x_i - 1) \cdot (x_i - 2) \cdots (x_i - 9) =0 \quad \forall i \in [0, 80]

(f(g^i) - 1) \cdot (f(g^i) - 2) \cdots (f(g^i) - 9) =0 \quad \forall i \in [0, 80]

g^i \: \text{are roots of} \: (f(x) - 1) \cdot (f(x) - 2) \cdots (f(x) - 9)

\exists p_0: \begin{cases} p_0 \: \text{is a polynomial}\\ (f(x) - 1) \cdot (f(x) - 2) \cdots (f(x) - 9) = (x - g^0) \cdot (x - g^1) \cdots (x - g^{80}) * p_0(x) \end{cases}

p_0: x \mapsto \frac {(f(x) - 1) \cdot (f(x) - 2) \cdots (f(x) - 9)} {(x - g^0) \cdot (x - g^1) \cdots (x - g^{80})} \; \text{is a polynomial}

Step 1

Group the constraints

cp: x \mapsto \alpha \cdot p_0 + \beta \cdot p_1 + \gamma \cdot p_2 \; \text{is a polynomial}

Let's say you have \( p_0 \), \( p_1 \) and \( p_2 \) contraints

Choose 3 random numbers \( \alpha , \beta \ , \gamma \)

Commit evaluations of \( cp \)

Step 2

FRI the constraints

or proving that \( cp \) is a polynomial

Proving that \( cp \) is a polynomial is hard, let's prove that it's close to a polynomial of low degree \( d \) instead

What's FRI anyways?

Proving \( f \) is close to a polynomial of low degree \( d \)

Proving \( g \) is close to another polynomial of low degree \( d / 2 \)

Receive a random number \( \alpha \) from the verifier

Separate \( f \) between odd and even exponents

\( f(x) = g(x^2) + x \cdot h(x^2) \)

f'(y) = g(y) + \alpha \cdot h(y)

Commit evaluations of \( f' \)

Step 1

Rince and repeat

dividing the degree \( d \) until \( d = 0 \)

...and commit the constant value of \( f \)

Step 2

Let it simmer for 2 hours

and serve it warm to the verifier

What are we serving to the verifier?

The trace commitment: \( Merkle(x_i \in [0, 80]) \)
The \( cp \) commitment: \( Merkle(cp(x)) \)
The commitment at all FRI steps
The constant value after applying FRI until \( d = 0 \)

What to serve with this?

Starkware's Stark101: https://starkware.co/stark-101/
Vitalik's Starks article series: https://vitalik.ca/general/2017/11/09/starks_part_1.html
Proving Brainf*ck: https://aszepieniec.github.io/stark-brainfuck/

Bon appétit !

No time left for questions but do reach out to me for easy questions or Eli for hard ones