Text
@BiancaGando

Intro to
Graphs
Concept
Graphs are a set of vertices connected by edges
Each item in the graph contains:
- Stored data -- aka node value
- Stored references -- aka relationships aka edges -- to zero or more other nodes
@BiancaGando

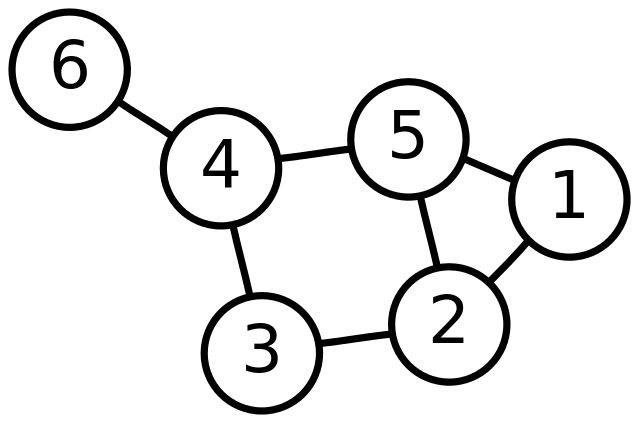
Vocabulary
@BiancaGando
Edges
represent the connection b/t 2 vertices
can be directed or undirected
Vertices
nodes in the graph
Path
a sequence of connected vertices
a simple path has no repeated vertices
Cycles
a path that is cyclical
an acyclic graph has no cycles
Text
@BiancaGando

Adding an edge
Deleting an edge
Detecting an edge
Finding the neighbors of a vertex
Finding a path between two vertices
Common Operations
@BiancaGando

Representing
Graphs
Text
@BiancaGando

Adjacency Matrix
Undirect Graph

Text
@BiancaGando

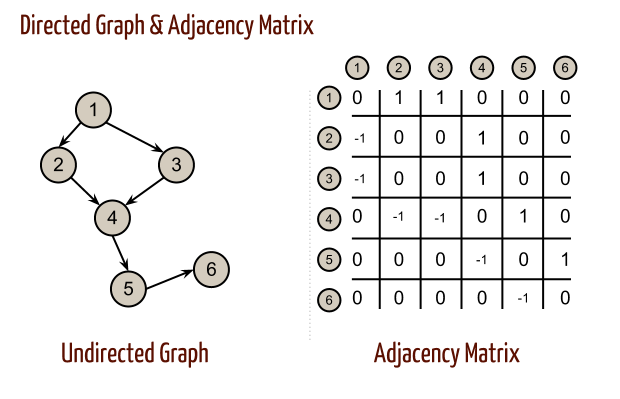
Adjacency Matrix
Directed Graph
@BiancaGando

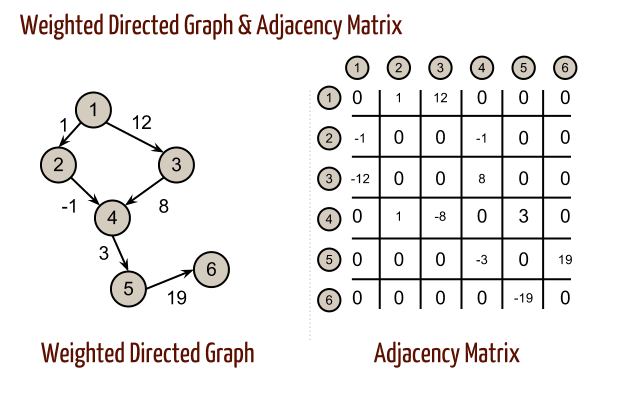
Adjacency Matrix
Weighted Directed Graph
@BiancaGando

Pseudocode
Constructor
addNode()
addEdge()@BiancaGando

Adjacency List
Directed Graph

@BiancaGando

Pseudocode
Constructor
addNode()
addEdge()Consider:
How could we represent (un)directed edges?
How could we represent weighted edges?
Exercise Time!
@BiancaGando

Text
@BiancaGando

Intro to
Depth-First Search
DFS
@BiancaGando

Why? Find paths, cycles, connectivity and more!
Concepts:
Explored (black), Visited (gray), Undiscovered (white)
Graph Traversing
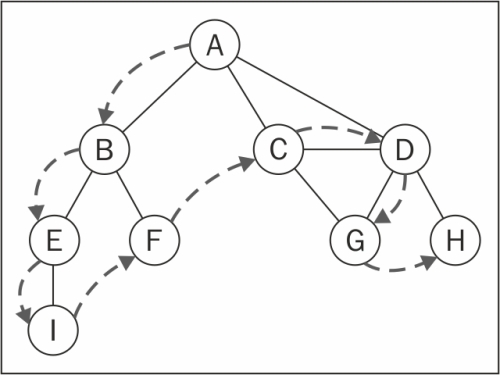
@BiancaGando

Pseudocode
//Code here
Exercise Time!
@BiancaGando

@BiancaGando

-
Mark v as discovered (grey).
-
For all unvisited (white) neighbors w of v:
-
Visit vertex w.
-
-
Mark v as explored (black).
Procedure

Complexity
Depth-First Search (DFS)
Time
Text
@BiancaGando

Intro to
Breadth-First Search
BFS
@BiancaGando

Concept: BFS
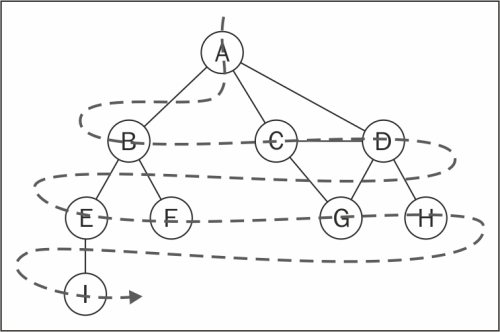
@BiancaGando

Diagram: BFS
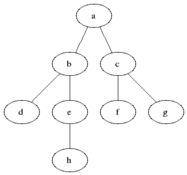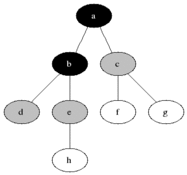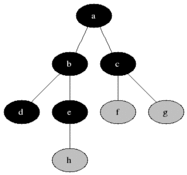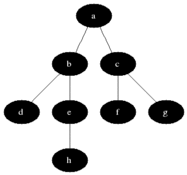
@BiancaGando

Pseudocode
//Code here
@BiancaGando

-
Create a queue Q.
-
Mark v as discovered (grey) and enqueue v into Q.
-
While Q is not empty, perform the following steps:
-
Dequeue u from Q.
-
Mark u as discovered (grey).
-
Enqueue all unvisited (white) neighbors w of u.
-
Mark u as explored (black).
-
Procedure

@BiancaGando

1. BFS Function
- queue
- recursion
2. Tree vs Graph Data Structure
Interface: BFS
@BiancaGando

O(n)
Time Complexity
@BiancaGando

Shortest path finding
Web crawlers
Use Cases: BFS
Exercise Time!
@BiancaGando

Recap
- DFS and BFS can be applied to graphs and trees
- information about how data is organized in the graph or tree can aid in determining whether to use DFS or BFS
- BFS can be implemented using helper data structures
- DFS can be implemented recursively and is the simpler of the two methods to implement
Recap
Concepts
Exercise Time!
@BiancaGando

