C++ & Algorithm
C++?
C++是許多語言的遠房親戚甚至老祖宗
許多學過C++的人都表示由C++跳至其他語言非常容易
因為C++剛好兼具了許多語言的風格
例如:
- 程序導向(按照步驟做)
- 物件導向、函數導向(把功能打包起來做)
- 泛型程式設計(讓電腦判斷型別)
C++?
但C++本身說難不難,說簡單也可以不簡單
不過呢~這堂課主要是訓練大家的程式邏輯、運算思維
C++只是作為一個速度夠快的結構化語言
讓大家學習對電腦來說怎樣是清楚、有效率的步驟
#include <iostream>
#include <algorithm>
using namespace std;
long long dp[100000], k, n, w, v;
int main() {
cin >> n >> k;
for(int i = 0; i < n; i++) {
cin >> w >> v;
for(int W = k; W >= w; W--) dp[W] = max(dp[W], dp[W-w] + v);
}
cout << dp[k] << '\n';
}Algorithm!
大家都知道電腦擁有超快速且準確的運算能力
實際上普通的電腦一秒大概可以執行\(10^9\)次的運算
但是呢~電腦執行的指令依舊是人們下達的
所以我們如果下錯指令,可能會無法達到預期的效果
一個演算法首先要有明確的步驟
並且保證能在有限的時間內結束
在做事的時候心中已有了個完整的流程圖
演算法的課程即是訓練此種邏輯思維
Algorithm!
分析演算法們的正確性及效率會用到一些數學
不過講師講的一定都可以讓大家聽懂的啦!
而且有許多國中、小可能就學過的東西
舉個簡單的例子
最大公因數
試除法
質因數分解法
輾轉相除法
短除法
試除法
質因數分解法
輾轉相除法
短除法
\(O(N)\)
\( \rightarrow O(\sqrt{N})\)
試除法
質因數分解法
輾轉相除法
短除法
\(O(N)\)
\( \rightarrow O(\sqrt{N})\)
\( O(\sqrt{N})\)
試除法
質因數分解法
輾轉相除法
短除法
\(O(N)\)
\( \rightarrow O(\sqrt{N})\)
\( O(\sqrt{N})\)
\( O(\sqrt{N})\)
試除法
質因數分解法
輾轉相除法
短除法
\(O(N)\)
\( \rightarrow O(\sqrt{N})\)
\( O(\sqrt{N})\)
\( O(\sqrt{N})\)
\( O(\log N)\)
Competitive Programming
利用各種語法和演算法來解決各式各樣的題目!
Judge
Green Judge
TIOJ Infor Online Judge
Codeforces
AtCoder
Zero Judge
......
Competition
HP codewars
能力競賽
NPSC
TOI / IOI
APCS(?
要教啥?
直接開始C++
工欲善其事,必先利其器
想要偷跑的請點這!
C++的輸出
教電腦說話
傳說中的Hello World!
#include<iostream>//引入C++ 輸出輸入的函式庫
using namespace std;//不知道
int main()//主函式 電腦會由上到下執行其中的內容
{
cout << "Hello world!" << endl;//輸出的啦
}剛剛出現的奇怪符號
- <<(endl 前也要)
- ;
- "
- #、()、{}
習題
a003
#include<iostream>
using namespace std;
int main()
{
cout << "^_^" << endl;
cout << ""o"" << endl;
cout << "\^o^/" << endl;
}CE(編譯錯誤)
傳說中的跳脫字元
What's the matter?
cout << ""o"" << endl;cout << "\"o\"" << endl;傳說中的跳脫字元
What's the matter?
cout << "\^o^/" << endl;cout << "\\^o^/" << endl;AC Code
#include<iostream>
using namespace std;
int main()
{
cout << "^_^" << endl;
cout << "\"o\"" << endl;
cout << "\\^o^/" << endl;
}
常見的跳脫字元
C++的變數
拿來裝值的容器
直接看程式碼
#include<iostream>
using namespace std;
int main()
{
int a = 5,b = 10;
string s = "Hi!";
float f = 3.614;
cout << a << " " << b << endl;
cout << s << endl;
cout << f << endl;
a = 1;
b = 11;
cout << a << " " << b << endl;
}常見的型態
C++的輸入
跟電腦說話
飯粒
#include<iostream>
using namespace std;
int main()
{
int a,b,c;
cin >> a >> b >> c;
cout << a + b + c << endl;
}
C++的加減乘除
就是加減乘除(還有趴)
飯粒
#include<iostream>
using namespace std;
int main()
{
int a = 5,b = 10;
cout << "a + b = " << a + b << endl;
cout << "a - b = " << a - b << endl;
cout << "a * b = " << a * b << endl;
cout << "a / b = " << a / b << endl;
cout << "a % b = " << a % b << endl;
double s = 1.05,t = 0.01;
cout << "s + t = " << s + t << endl;
cout << "s - t = " << s - t << endl;
cout << "s * t = " << s * t << endl;
cout << "s / t = " << s / t << endl;
}
例題
if/else if/else 判斷式
如果/要不然如果/要不然
飯粒
#include<iostream>
using namespace std;
int main()
{
int a,b,c;
cin >> a >> b >> c;
if(a >= b && b >= c)
{
cout << a << endl;
}
else if(b >= c)
{
cout << b << endl;
}
else
{
cout << c << endl;
}
}
比較運算子
- <、>、<=、>=、==
- = : 賦值
- == : 判斷左右兩邊的值是否一樣
邏輯運算子
and &&
or ||
一行可省略大括號
#include<iostream>
using namespace std;
int main()
{
int a,b,c;
cin >> a >> b >> c;
if(a >= b && a >= c)
cout << a << endl;
else if(b >= c)
cout << b << endl;
else
cout << c << endl;
}例題
while 迴圈
當
烏龜恆等式
while = if * n
while飯粒
#include<iostream>
using namespace std;
int main()
{
int i = 0;
while(i < 10)
{
cout << i <<endl;
i++;
}
}
例題
for 迴圈
對於
for 飯粒
#include<iostream>
using namespace std;
int main()
{
int i;
for(i = 0;i < 10;i++)//用要分號隔開喔!
{
cout << i << endl;
}
}
前人種樹,後人乘涼
例題
Array 陣列
很多變數
會飛恆等式
"int arr[N];" == "int a;"*N
簡單題
輸入一個正整數n,然後輸入n個數字(\(n\leq 5\))
把這n個數字的順序顛倒,然後輸出
if-else 地獄
呃...開n個變數?
#include <iostream>
using namespace std;
int main() {
int n;
int a,b,c,d,e;
cin >> n;
if(n == 1) {
cin >> a;
cout << a << endl;
}else if(n == 2) {
cin >> a >> b;
cout << b << ' ' << a << endl;
}else if(n == 3) {
cin >> a >> b >> c;
cout << c << ' ' << b << ' ' << a << endl;
}else if(n == 4) {
cin >> a >> b >> c >> d;
cout << d << ' ' << c << ' ' << b << ' ' << a << endl;
}else if(n == 5) {
cin >> a >> b >> c >> d >> e;
cout << e << d << ' ' << c << ' ' << b << ' ' << a << endl;
}
}陣列!
當一大堆變數的用途都差不多,我們可以為他們一起開一個空間,宣告時共用一個名字,用數字代表是哪個變數
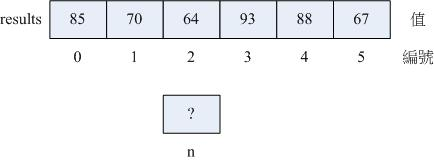
陣列!
分辨不同格子的編號稱為索引。注意!陣列的索引值是從 0 開始編號,稱為 \(\textbf{0-base}\)。也就是說:
索引值為0時,代表第1個變數
索引值為1時,代表第2個變數
索引值為2時,代表第3個變數

陣列!
宣告的語法是 \(\texttt{int arr[Size];}\)
常常會搭配for迴圈使用
#include <iostream>
using namespace std;
int main() {
int n,i,a[5];
cin >> n;
// 合法的索引是0,1,...n-2,n-1,因此我們常用以下這種迴圈
for(i = 0; i < n; i++)
cin >> a[i];
for(i = n-1; i >= 0; i--)
cout << a[i] << ' ';
cout << endl;
}例題
分組
三個湊裨將,勝過一個諸葛亮
三個臭皮將,勝過一個諸葛亮
1. 三個臭皮將,湊成豬革梁
2.三個湊裨將,勝過一個諸葛亮
用同一張桌子的人一組
沒組員話就加入最近的一組吧~!
(一組最多三人喔)
分組要幹嘛?
排序
終於有一個像演算法的東西了?
其實也是語法
將A陣列的第a項到第b項排序好
sort(A+a,A+b+1);開頭記得加上這行
#include<algorithm>排好陣列的前N項
#include<iostream>
#include<algorithm>//別忘記!
using namespace std;
int main()
{
int N,i;
int A[100009];//宣告陣列
cin >> N;
for(i = 0;i < N;i++)
{
cin >> A[i];
}
sort(A,A+N);
for(i = 0;i < N;i++)
{
cout << A[i] << " ";
}
cout << endl;
}
演算法初體驗
這次感覺真的比較像演算法
輸入一個長度為N的序列,並問你某一個數字是否在該序列中?
input:
5
3 1 4 7 5
6
output:
No
怎麼做?
用陣列就解決啦!
(講師:懶得放code)
稍微改一下題目
輸入一個長度為N的序列,並問你某Q個數字是否在該序列中?
input:
5
3 1 4 7 5
2
6 5
output:
No
YES
先跳出來一下
複雜度分析
複雜度是甚麼?
算出操作的次數,並把係數拿掉
操作包含輸入、輸出、改值、
運算......
不要完全相信我說的話!
前綴和
#include<iostream>
#include<algorithm>
using namespace std;
int A[1009],S[1009];//宣告陣列(初始值為零)
int main()
{
int N,i;
cin >> N;
for(i = 1;i <= N;i++)
{
cin >> A[i];
S[i] = S[i-1] + A[i];
}
for(i = 1;i <= N;i++)
{
cout << S[i] << " ";
}
cout << endl;
}
\(aN+b \Rightarrow N\)
\(O(N)\)
#include<iostream>
#include<algorithm>
using namespace std;
int A[1009];//宣告陣列(初始值為零)
int main()
{
int N,i,k,ans = 0,j;
cin >> N;
for(i = 1;i <= N;i++)
{
cin >> A[i];
}
cin >> k;
for(i = 1;i <= N;i++)
{
for(j = i + 1;j <= N;j++)
{
if(A[i] +A[j] == k)
{
ans++;
}
}
}
cout << ans << endl;
}
\(aN^2 + bN + c \Rightarrow N^2\) \( O(N^2) \)
通常電腦每秒可以跑
\(10^8\)個操作喔!
回到剛剛的題目
輸入一個長度為N的序列,並問你某Q個數字是否在該序列中?
input:
5
3 1 4 7 5
2
6 5
output:
No
YES
*每個數字不超過C
有甚麼好方法?
*複雜度越低越好喔!
hint : sort() 的複雜度是 O(\(N log N\))
有O(N+C+Q)的做法喔!
#include<bits/stdc++.h>
using namespace std;
int cnt[100009];
int main()
{
int N,i,j,k,Q;
cin >> N;
for(i = 0;i < N;i++)
{
cin >> k;
cnt[k] = 1;
}
cin >> Q;
for(i = 0;i < Q;i++)
{
cin >> k;
if(cnt[k] == 1)
{
cout << "YES" << endl;
}
else
{
cout << "NO" << endl;
}
}
}
二分搜
首先!
把給的序列sort
不排白不排
猜數字 (終極密碼)
每次把區間劈成兩半
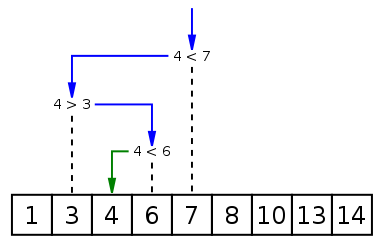
#include <iostream>
int main() {
int N, Q, A[100000], i, x;
cin >> N >> Q;
for(i = 0;i < N;i++) cin >> A[i];
sort(A,A+N);
for(i = 0;i < Q;i++) {
cin >> x;
int L = 0, R = N-1, ok = 0;
while(L <= R) {
int mid = (L+R)/2;
if(A[mid] < x)
L = mid+1;
else if(A[mid] >= x)
R = mid;
}
if(A[L] == x) cout << "Yes" << endl;
else cout << "No" << endl;
}
}再進一步
給一個序列 [a1,a2,...,an],詢問 q 個 x
回答至少要選幾個數字,總和才會不小於 x
- 對於一個 x 想算最少要幾個數字很難,但是對於選 k 個數字要算他們的最大總和是簡單的
- x 越大,需要的數字也越多(單調性)
二分搜!
每次看「選了 mid 個數字總和有沒有超過 x」
如果有就 r = mid (表示至多mid就足夠了)
否則 l = mid+1 (表示要比mid多才夠)
這種技巧稱為對答案二分搜,通常是題目必須求最小次數等情況使用,注意必須有單調性才能使用二分的技巧喔!
不一定要寫的麻煩例題
Greedy
人心不足蛇吞象
這個演算法就是貪心這個想法本身!
也有人說這個演算法是找出區域最好,進而得到全域最好。
練習製造完美
給你n個物體,第\(i\)個物體的重量是\(w_i\),選擇盡量多的物體(只能拿整數個),使總重不超過C。
給你\(n\)個物體,第\(i\)個物體的重量是\(w_i\),價值是\(v_i\),選擇一些物體(可以拿一個物體的任意部分),使總重不超過\(C\),且價值和最大。
若拿一個物體的\( \frac{a}{b}(a \leq b)\),則其重量為\(w_i \times \frac{a}{b}\),獲得價值為\(v_i \times \frac{a}{b}\)
有\(n\)個人,其中第\(i\)個人重量是\(w_i\),每艘船最多坐兩個人,而且每艘船最高在重量均為\(C\)(\(C\)大於\(w_i\)的最大值),用最少的船裝載所有人。
數線上有n個線段,其中第\(i\)個線段的左右界分別是是\(l_i,r_i\),選最多線段,使得這些線段兩兩不相交
數線上有n個線段,其中第\(i\)個線段的左右界分別是是\(l_i,r_i\),選擇一些點,使得每條線段至少包含一個點。
字元、字串
character / string
C++ 中用單引號代表字元
型別是 char (但是內部儲存還是數字)
#include <iostream>
using namespace std;
int main() {
char c = 'a';
cout << c << endl;
int i = 'z';
cout << i << endl;
}雙引號代表的則是字串!
我們可以用string型別來儲存字串
#include <iostream>
using namespace std;
int main() {
string s = "J12Z";
cout << s << endl;
cin >> s;
cout << "GZ " << s << endl;
}字串的本質是字元的陣列
所以它有長度,可以用方括號存取第i個字元是什麼
(注意不要讓[]裡面的i>=字串的length()!)
#include <iostream>
using namespace std;
int main() {
string s = "J12Z";
cout << s.length() << endl;
cout << s[0] << 'I' << s[3] << s[3] << endl;
// s[4] 超出陣列外,有機會 RE !
}Function
函數!
不知道大家有沒有聽過 C (組合數) ?
#include <iostream>
using namespace std;
int main()
{
long long above = 1, below = 1, n, r, i;
cin >> n >> r;
for(i = 1; i <= n; i++)
{
above *= i;
}
for(i = 1; i <= r; i++)
{
below *= i;
}
for(i = 1; i <= n-r; i++)
{
below *= i;
}
cout << above/below << '\n';
}
不要重複自己!
Do not Repeat Yourself
#include <iostream>
using namespace std;
long long fac(int n) { // return n!
long long ans = 1, i;
for(i = 1; i <= n; i++) {
ans *= i;
}
return ans;
}
int main() {
int n,r;
cin >> n >> r;
cout << fac(n)/(fac(r)*(fac(n-r))) << '\n';
}#include <iostream>
using namespace std;
long long fac(int n) { // return n!
long long ans = 1, i;
for(i = 1; i <= n; i++) {
ans *= i;
}
return ans;
}
long long C(int n,int r) { // return C_r^n
return fac(n) / (fac(r)*fac(n-r));
}
int main() {
int n,r;
cin >> n >> r;
cout << C(n,r) << '\n';
}long long fac(int n) { // return n!
long long ans = 1, i;
for(i = 1; i <= n; i++) {
ans *= i;
}
return ans;
}回傳型別(你回傳的東西是什麼型態)
參數(你傳了什麼東西進來)
return的時候就會結束這個函數,回傳該回傳的東西給呼叫他的地方
中間一樣可以用迴圈、if、else等等
void pyramid(int n = 5) {
int i,j;
for(i = 1; i <= n; i++) {
for(j = 1; j <= i; j++) {
cout << '*';
}
cout << '\n';
}
}
int main() {
pyramid();
pyramid(3);
pyramid(10);
}參數型別和回傳型別都可以是void喔!
代表不接收參數或不回傳東西
你看過的函數
- log
- sin、cos、tan?
- main
函數裡面還可以呼叫別的函數
甚至呼叫自己(稱為遞迴)
不過下次再講(?
Recursion
遞迴!
遞迴
一個函數呼叫自己
int f(int x)
{
return f(x-1) + f(x-2);
}遞迴雙要素
1.終止條件
2.遞迴!(別忘了這是遞迴!)
int f(int x)
{
if(x == 1 || x == 2) return 1;
return f(x-1) + f(x-2);
}相信自己!
int gcd(int a,int b)
{
if(b == 0) return a;
return gcd(b,a%b);
}Clean Code
好好排版好嗎(X
縮排 Indent
縮排簡單來說就是在結構化指令的區塊加上前綴的tab鍵或空白以便閱讀
下面這段程式碼真是醜的極致,完全沒有縮排,很難看到哪個if對到哪個else或大括號怎麼包含的
#include <iostream>
using namespace std;
int main() {
int i,j;
cin>>i>>j;
if(i==0){
if(j%2==1){
cout<<i+j<<endl;
}else{
cout<<i-j<<endl;
}
}
else{
cout<<"NO"<<endl;
}
}縮排 Indent
舒服多了! 這裡用的是tab縮排,程式的結構一目了然
#include <iostream>
using namespace std;
int main() {
int i,j;
cin >> i >> j;
if(i == 0) {
if(j%2 == 1) {
cout << i+j << endl;
}else {
cout << i-j << endl;
}
}else {
cout << "NO" << endl;
}
}縮排 Indent
有些語言中必須要縮排才是正確的語法,例如python、YAML、Haskell等
C++並沒有硬性規定要如何縮排,但是縮排能夠幫助程式碼的閱讀,不論是自己之後看或是給別人理解都非常有助益。
變數命名
有時常常會因為變數只取一個英文字母導致自己不知道他是做什麼用的,為了這個加上的註解都是「笨註解」
在變數命名時可以盡量考量這個變數的作用,例如:年分可以命名為year, yy, Y,或者線段可以叫做segment, seg, S。
取用長的命名或短的,原則上是範圍越大的變數,命名要越長、越清晰;反之則可以越短越重複,例如單個迴圈的計數變數我們幾乎都會命名為 i,而若在全域變數出現了t,u,v,我們幾乎無法想像那是什麼用途的變數。
// dreamoon_love_AA的code,醜到slides都不知道這是C++(X
#include<iostream>
#define CASET int ___T; scanf("%d", &___T); for(int cs=1;cs<=___T;cs++)
#define REP(I, N) for (int I = 0; I < (N); ++I)
void R(int &x) { scanf("%d", &x); }
void W(const int &x) { printf("%d", x); }
int main(){
CASET{
int AA[5];
REP(i,5)R(AA[i]);
if((AA[0]+AA[2]-1)/AA[2]+(AA[1]+AA[3]-1)/AA[3]>AA[4])W(-1);
else W((AA[0]+AA[2]-1)/AA[2],(AA[1]+AA[3]-1)/AA[3]);
}
return 0;
}#include <algorithm>
#include <cassert>
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T-- > 0) {
int A, B, C, D, K;
cin >> A >> B >> C >> D >> K;
bool success = false;
for (int X = 0; X <= K; X++) {
int Y = K - X;
if (X * C >= A && Y * D >= B) {
success = true;
cout << X << ' ' << Y << '\n';
break;
}
}
if (!success)
cout << -1 << '\n';
}
}大括號?
#include <iostream>
using namespace std;
int main() {
int n,i,a[5];
cin >> n;
for(i = 0; i < n; i++) {
cin >> a[i];
}
for(i = n-1; i >= 0; i--) {
cout << a[i] << ' ';
}
cout << endl;
}#include <iostream>
using namespace std;
int main()
{
int n,i,a[5];
cin >> n;
for(i = 0; i < n; i++)
{
cin >> a[i];
}
for(i = n-1; i >= 0; i--)
{
cout << a[i] << ' ';
}
cout << endl;
}兩種style:換行or不換行(p.s.有一個講師最不喜歡大括號,能不加就不加)
空格
#include < iostream >
using namespace std;
int main() {
int n, i, a [ 5 ];
cin >> n;
for( i = 0; i < n; i ++ ) {
cin >> a [ i ];
}
for( i = n - 1; i >= 0; i -- ) {
cout << a [ i ] << ' ';
}
cout << endl;
}#include<iostream>
using namespace std;
int main(){
int n,i,a[5];
cin>>n;
for(i=0;i<n;i++){
cin>>a[i];
}
for(i=n-1;i>=0;i--){
cout<<a[i]<<' ';
}
cout<<endl;
}空格有些人喜歡加爆,有些人死都不加
註解
#include <iostream>
using namespace std;
// 下面這段程式把一段數字倒過來輸出
int main() {
int n,i,a[5];
cin >> n;
for(i = 0; i < n; i++) {
cin >> a[i];
}
for(i = n-1; i >= 0; i--) {
cout << a[i] << ' ';
}
cout << endl;
}通常用大綱就好,除非是函式的使用方法或注意事項等需要多一些說明的東西
註解每一行的作用很製杖(
動態規劃 OwO
什麼是動態規劃(DP)?
- 對於一個問題,我們發現它有遞迴的性質(可以把大問題拆成小問題)
- 小問題的數量很多,會重複算到
- 把小問題的答案存下來!
簡單的問題
有個 n 階段的階梯,一次可跨上 1 或 2 個階段,
問有多少種不同的方式,踏上第 n 階段。
\(dp[n] = dp[n-1] + dp[n-2]\)
\(dp[0] = dp[1] = 1\)
再一個簡單的問題
有個 n 階段的階梯,一次可跨上 1 或 2 個階段,
並且每一階段都有一個事件,可能會讓你增加或減少金錢
問走到第 n 階的過程中最多能獲益多少?
\(dp[n] = \max(dp[n-1] + dp[n-2]) + val_n\)
\(dp[0] = 0\)
\(dp[1] = val_1\)
怎麼寫?
int dp[1000];
int main() {
int i,n;
cin >> n;
dp[0] = dp[1] = 1;
for(i = 2; i <= n; i++) dp[i] = dp[i-1]+dp[i-2];
cout << dp[n] << '\n';
}int dp[1000];
int DP(int n) {
if(dp[n]) return dp[n];
dp[n] = DP(n-1)+DP(n-2);
return dp[n];
}
int main() {
int i,n;
cin >> n;
dp[0] = dp[1] = 1;
cout << DP(n) << '\n';
}int dp[1000],val[1000];
int main() {
int i,n;
cin >> n;
for(i = 1; i <= n; i++) cin >> val[i];
dp[0] = 0;
dp[1] = val[1];
for(i = 2; i <= n; i++) dp[i] = max(dp[i-1]+dp[i-2]) + val[i];
cout << dp[n] << '\n';
}int dp[1000],val[1000],calced[1000];
int DP(int n) {
if(calced[n]) return dp[n];
dp[n] = max(DP(n-1)+DP(n-2)) + val[n];
calced[n] = 1;
return dp[n];
}
int main() {
int i,n;
cin >> n;
for(i = 1; i <= n; i++) cin >> val[i];
dp[0] = 0;
dp[1] = val[1];
calced[0] = calced[1] = 1;
cout << DP(n) << '\n';
}更多經典
給一個長度 n 的序列
問裡面一個連續的區間總和最多是多少?(不能不拿)
\(dp[i] = \max(dp[i-1], 0) + val_i\)
\(dp[0] = 0\)
更多經典
小小小小小競賽
Title Text
題解OAO
pA b970: 我不說髒話 (續)
#include <iostream>
using namespace std;
int main() {
int n,i;
cin >> n;
for(i = 1; i <= n; i++)
cout << i << ". I don't say swear words!" << endl;
}pB a782: 4. Redundant Acronym Syndrome Syndrome
getline函式...
cin.getline(str) getline(cin, str) getline(cin, str, delim)
成功讀到一行的字串之後
可以紀錄哪些是要輸出的
#include <iostream>
using namespace std;
int main() {
string str;
while(1) {
getline(cin, str);
if(str == "END") break;
int i, last = 0;
cout << char(str[0]-'a'+'A');
for(i = 1; i < str.size(); i++) {
if(str[i-1] == ' ') {
cout << char(str[i]-'a'+'A');
last = i;
}
}
cout << ' ';
for(i = last; i < str.size(); i++)
cout << str[i];
cout << endl;
}
}stringstream
#include <iostream>
#include <sstream>
using namespace std;
int main() {
string str;
while(1) {
getline(cin, str);
if(str == "END") break;
stringstream ssin(str);
while(ssin >> str) {
cout << char(str[0]-'a'+'A');
}
cout << ' ' << str << endl;
}
}pD b971: 等差數列
#include <iostream>
using namespace std;
int main() {
int a1, an, d, i;
cin >> a1 >> an >> d;
for(i = a1; i != an; i += d) {
cout << i << ' ';
}
cout << an << endl;
}pD b971: 等差數列
需要注意的事情
- 公差可能是0
- 公差可能是負的
- 所以末項不一定比首項大
pC c575: APCS 2017-0304-4基地台
首先想到一個\(\mathcal{O}(nc)\)的解
從小到大檢查一個半徑可不可行
把座標從左到右排序
可以知道最左邊的基地台一定越右邊越好
但是必須包含最左邊的服務點
pC c575: APCS 2017-0304-4基地台
可以發現! 如果一個半徑r可行
那比r大的半徑都可行
二分搜半徑!
int l = 0, r = 100000000; // [l,r]
while(l < r) {
int mid = l+(r-l)/2;
if(ok(mid))
l = mid;
else
r = mid-1;
}
cout << l << endl;為了預防大家不知道怎麼二分搜這邊放了大概的框架
只要把ok這個檢查用的函數寫好就好
???
不知道做什麼就來做題目ㄅ
STL
vector(動態陣列)
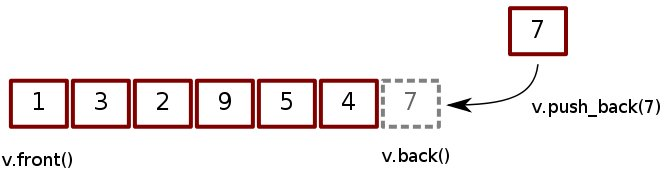
#include<vector>//記得!
#include<iostream>
int main(){
vector<int> vec;//宣告
for(int i=0 ; i<5 ; i++){
vec.push_back(i * 10); // [0, 10, 20, 30, 40]
}
vec.pop_back(); // 移除 40
vec.pop_back(); // 移除 30
for(int i=0 ; i<vec.size() ; i++){ // vec.size() = 3
cout << vec[i] << endl; // 輸出 0, 10, 20
}
cout << vec.front() << " " << vec.back() << endl;
}set(集合)
- insert: 把一個數字放進集合
- erase: 把某個數字從集合中移除
- count: 檢查某個數是否有在集合中
- \(O(\log N)\)
#include <set>//記得
#include<iostream>
using namespace std;
int main(){
set<int> mySet;
mySet.clear();
mySet.insert(20); // mySet = {20}
mySet.insert(10); // mySet = {10, 20}
mySet.insert(30); // mySet = {10, 20, 30}
cout << mySet.count(20) << endl; // 存在 -> 1
cout << mySet.count(100) << endl; // 不存在 -> 0
mySet.erase(20); // mySet = {10, 30}
cout << mySet.count(20) << endl; // 0
for(auto t : mySet){
cout << t << " "; //{10, 30}
}
cout << endl;
}map(地圖,神奇陣列)
#include <map>
#include <iostream>
using namespace std;
int main(){
map<string, int> m; // 從 string 對應到 int
m["one"] = 1; // "one" -> 1
m["two"] = 2; // "two" -> 2
m["three"] = 3; // "three" -> 3
cout << m["one"] << endl; // 1
cout << m["three"] << endl; // 3
cout << m["ten"] << endl; // 0 (無對應值)
}Practice
試著攻略Greenjudge(?
圖 (Graph)
什麼是圖?
- 和平常看到那些美美的圖或者3D圖不同,演算法當中最常提到的圖比較抽象,通常代表物件之間的「關係」
- 圖有頂點(Vertex)和邊(Edge),頂點的集合記為 \(V\) ,邊的集合記為 \(E : V \times V = \{(u_i, v_i)\}\)
- 邊有方向的話稱為有向圖,否則稱為無向圖
- 每個點有多少往外連的邊,稱為它的「出度」;有多少邊連進來則稱「入度」。無向圖不分出入,只稱「度數」
- 一條邊如果連接兩個相同的頂點,稱為自環(自己連向自己);如果存在重複的邊稱為重邊。沒有重邊或自環的圖稱為簡單圖
什麼是圖?
什麼是圖?
這邊的名詞不同地方可能會有小差異,不要太在意XD
- 路徑:從某個點\(u\)經過一些邊走到\(v\),如果是有向圖當然不能反著走
- 行跡:不經過重複邊的路徑
- 簡單路徑:不經過重複點的路徑
- 環:起點和終點相同,且除了起點和終點以外沒有經過重複點的路徑
什麼是圖?
- 連通:在無向圖中,我們說 \(u, v\)連通若且惟若有一條路徑可以從\(u\)到\(v\)。如果一群頂點兩兩連通,我們也可以說這群頂點是連通的。整張圖都連通的話可以稱做連通圖
- 連通塊:包含某個頂點\(u\)且包含所有和\(u\)連通的點的頂點集合,我們通常稱為連通塊或連通分量
- 弱連通:在有向圖中,如果一群頂點中存在一個點\(u\)走的到其他所有點,我們稱這群頂點是弱連通的。另外一種等價的描述是:一群頂點是弱連通的若且惟若,這群頂點中每一對\((u,v)\)的都能從\(u\)走到\(v\)或從\(v\)走到\(u\)。可以想想為甚麼等價XD
- 強連通:一群頂點中,如果頂點兩兩之間都能互相走到,則稱為他們是強連通的
快問快答
- 一張簡單圖的頂點數量(\(|V|\)),和邊的最大數量關係是什麼?
- 無向圖中,頂點\(v\)的度數記為\(\deg(v)\),請問\(\sum_{v\in V}\deg(v)\)和邊的數量\(|E|\)有何關係?
- 最少要多少條邊才能讓一張\(n\)個頂點的無向圖成為一張連通圖?
- 在簡單無向圖中,一個環最小有多大?
不要偷看答案(#
- \(\max|E| = \frac{|V|(|V|-1)}{2}\)
- \(\sum_{v\in V}\deg(v) = 2|E|\)
- \(n-1\)
- \(3\)
特別的圖
特別的圖
- 樹:以下任何一個敘述都等價,符合這些條件的無向圖我們稱為樹。今天不會提太多樹的東西,不過等價性值得想一下如何證明。
- 連通且 \( |V| = |E| + 1 \)。
- 任意兩個點之間存在唯一的簡單路徑。
- 連通,但去掉任意一條邊就不連通。
- 沒有環,但加上任意一條邊就有環。
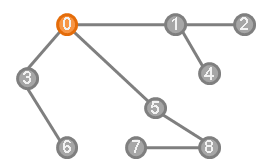
圖的儲存 & 遍歷!
最常用來儲存圖的方法有兩種
- 鄰接矩陣:開一個 \(|V| \times |V|\)的二維陣列\(M\),\(M[i][j]\)是0或1代表頂點\(i,j\)是否相連
- 鄰接串列:對於每個頂點,我們開一個list或者可變長度陣列,在C++中常用 \(\verb`vector`\)
https://tioj.ck.tp.edu.tw/problems/1831
(不要排斥TIOJ喔QQ)
圖的儲存 & 遍歷!
#include <iostream>
#include <algorithm>
#include <vector>
#define sort_uni(v) sort(begin(v),end(v)), v.erase(unique(begin(v),end(v)),end(v))
using namespace std;
const int N = 501;
int n,m,k;
vector<int> adjL[N]; // 鄰接串列(?)
bool adjM[N][N]; // 鄰接矩陣
string s;
void addEdge(int a,int b){
adjM[a][b] = true;
adjL[a].push_back(b);
}
signed main(){
cin >> n >> m >> k;
for(int i = 0, a, b; i < m; i++) {
cin >> a >> s >> b;
if(s.front() == '<') addEdge(b,a);
if(s.back() == '>') addEdge(a,b);
}
if(k) {
for(int i = 1; i <= n; i++) {
cout << i << " ->";
if(adjL[i].size() == 0)
cout << " 0\n";
else {
sort(adjL[i].begin(), adjL[i].end());
for(int j = 0; j < adjL[i].size(); j++) {
if(j == 0 || adjL[i][j] != adjK[i][j-1])
cout << ' ' << adjL[i][j];
}
cout << '\n';
}
}
}else {
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++)
cout << adjM[i][j] << " \n"[j==n];
}
}如果忘記\(\verb`vector`\)或function的語法可以翻前面!
沒教到的話錯在我身上(掩面
圖的儲存 & 遍歷!
深度優先搜尋(DFS)
走到一個頂點之後,會試圖往下一個頂點走,不得已才會往回走,能走得距離起點越深越好
怎麼實作呢?C++中直接利用函數遞迴正好符合這樣的要求,另一個方法是利用 \(\verb`stack`\)
vector<int> adj[N];
bool vis[N];
void dfs(int u) {
if(vis[u]) return; // 已經走過就不要再走了,以免繞圈圈陷入無窮迴圈
vis[u] = true;
cout << "now at " << v << '\n';
for(int v: adj[u])
dfs(v); // 遞迴呼叫dfs,在回到u以前嘗試走所有的v
}圖的儲存 & 遍歷!
深度優先搜尋(DFS)
走到一個頂點之後,會試圖往下一個頂點走,不得已才會往回走,能走得距離起點越深越好
怎麼實作呢?C++中直接利用函數遞迴正好符合這樣的要求,另一個方法是利用 \(\verb`stack`\)
vector<int> adj[N];
bool vis[N];
void dfs(int u) {
stack<int> s;
vis[s] = true;
s.push(u);
while(!s.empty()) {
int now = s.top(); s.pop();
cout << "now at " << now << endl;
for(int nxt: adj[now]) {
if(!vis[nxt]) {
vis[nxt] = true;
s.push(nxt);
}
}
}
}圖的儲存 & 遍歷!
廣度優先搜尋(BFS)
走到一個頂點之後,先看過所有鄰居,不得已才會走距離更遠的地方,走得越廣越好,可以保證走到每一個頂點的時候都是走最短的路徑
通常利用 \(\verb`queue`\)實作。什麼?那是什麼?\(\verb`queue`\)是一個先進先出的資料結構,它就像是排隊的顧客,先進來的顧客會先處理,包含在C++標準函式庫中
因此,我們每遇到一個頂點,我們就將所有沒造訪過的鄰居丟進\(\verb`queue`\),由於距離起點比較近的點一定會位在\(\verb`queue`\)比較前面的位置,我們可以保證距離比較近的會先被處理
圖的儲存 & 遍歷!
vector<int> adj[N];
bool vis[N];
int dis[N];
void dfs(int start) {
queue<int> q;
vis[start] = true;
dis[start] = 0;
q.push(start); // 把「檢查start的鄰居!」這件事丟進queue
while(!q.empty()) {
int now = q.front(); q.pop(); // 看現在應該先檢查誰的鄰居
for(int nxt: adj[now]) {
if(!vis[nxt]) { // 如果檢查到沒有造訪過的鄰居就丟進queue裡面,之後再看他的鄰居
vis[nxt] = true;
dis[nxt] = dis[now]+1;
q.push(nxt);
}
}
}
}圖的儲存 & 遍歷!
如果真的不知道怎麼寫就來看code吧><不要照抄喔!
TIOJ 1369 https://pastebin.com/DFyE1UPu
TIOJ 1022 https://pastebin.com/MtbknaC6