FFT與生成函數
生成函數
Basic Idea
簡單的乘法公式蘊含排列組合的意義
Definition
定義一個數列 \(\langle a_n \rangle\)的一般生成函數如下
(又稱形式幂級數、組合生成函數)
順便定義 \(x^k\) 的係數是 \(F[x^k] = a_k\)
\(a_n \in F\)
聽說 F 要是一個 Field
還有這邊先不要管 x 收不收斂
加法減法應該不用解釋吧@@
Multiplication
可以想成 \(a_n\) 就代表「拿 \(n\) 個的方法數」
那如果現在有兩種物品,拿 \(n\) 個的方法數分別是 \(a_n, b_n\)
那麼我們把他們乘在一起得到的多項式就代表總共拿了 \(n\)個的方法數
m(_ _)m
隨便啦,反正就是卷積
Practice
- \(a_i = [i = 0]\)
- \(a_i = 1\)
- \(a_i = C(n, i)\)
- \(a_i = \alpha^i\)
- \(a_i = i\)
- 現在有三種水果,分別有 \(a\)個、\(b\)顆、\(c\)粒,兩種方案被視為不同若且惟若至少有一種水果的數量不同,請寫出拿「總共數量為 \(n\) 的水果」方法數的生成函數
- 傳說中好吃的蛋餅,一次只能買奇數個,請寫出買 \(n\) 個蛋餅可能的購買方法的生成函數
- 不要給出包含sigma符號的答案喔> <
Example
費式數列?
\[a_0=0, a_1=1, a_n=a_{n-1}+a_{n-2}\]
Example
卡特蘭數
不同構的n個節點二元樹的數量
Common Tricks - Elementary
部分分數
咦?我不會除法QQ
其中 \(\alpha, \beta\)是分母的兩個根
review: \(\cfrac{1}{1-rx} = \sum\limits_{k=0}^\infty{r^kx^k}\)
所以 \(F[x^n] = A\alpha^n + B\beta^n\)
Common Tricks - Calculus
微積分!

微分 - 簡介
「惟天下之靜者乃能見微而知著。」
若\(f(x)\)(\(f\))為一個函數,則將\(f\)的微分寫作\(f'\)。
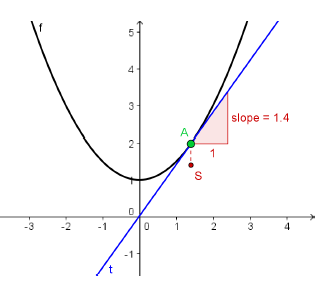
微分代表
一個函數的斜率
微分 - 規則
(notation) \(\frac{\text{d}f}{\text{d}x}\) 為
「若變化\(x\)的值一點點,那\(f\)會變化多少?」
(單項式微分)
(連鎖律)
(乘法)
(加法)
Note: \(f\circ g = f(g)\)
Ex. 簡簡單單
若\( a_i = i\),請找出\(\langle a_i\rangle\)的生成函數?
所以\(\frac{1}{(1 - x)^2}\)即為所求!
Ex. 比較不簡簡單單
若\( a_i = i^2\),請找出\(\langle a_i\rangle\)的生成函數?
但是 還不夠耶
Ex. 比較不簡簡單單
若\( a_i = i^2\),請找出\(\langle a_i\rangle\)的生成函數?
只是需要一點巧思嘛!
積分 - 簡介
「積土成山,風雨興焉;積水成淵,蛟龍生焉;積而算之,題AC焉」
若\(f\)為一個函數,則將\(f\)的積分寫作\(\int f\)。
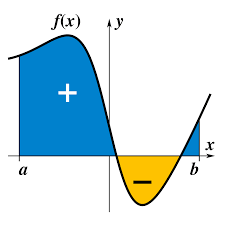
積分代表
一個函數地下的面積
積分 - 規則
(單項式微分)
(分布積分)
(加法)
積分和微分互為反運算!
習題省略 反正跟微分差不多
FFT與基本運算(?
\(O(n)\) (trivial)
- 加減
- 微分
- 積分
- 平移(乘或除 \(x^k\))
Was ist FFT?
Point-Value representation
Coefficient representation
\((a, f(a)), (b, f(b)), \dots (jizz, f(jizz))\)
\( f(x) = \sum a_kx^k\)
運算簡單
運算不簡單
推 >< by Sean
Was ist FFT?
Point-Value representation
Coefficient representation
乃衣服:\(O(n^2)\)
FFT:\(O(n \log n)\)
Was ist FFT?
Definitions & Basic Properties
讀:\(n\)次原根的\(k\)次方
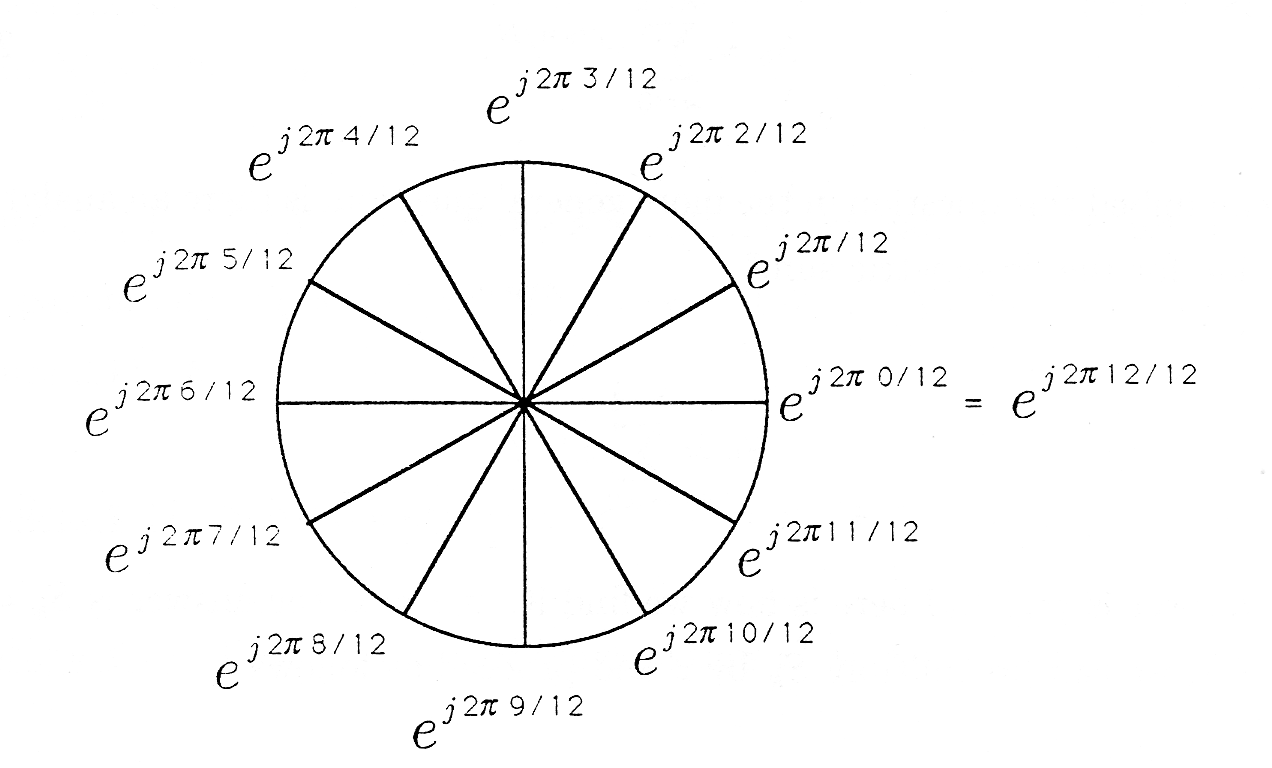
- 若\(n\)為偶數,則\(\omega^{k + \frac{n}{2}}_{n} = -\omega^k_n\)
- 若\(x \in \mathbb{N}\),則\(\omega^{k + xn}_{n} = \omega^k_n\)
- 若\(x \in \mathbb{N}\),則\(\omega^{xk}_{xn} = \omega^k_n\)
Was ist FFT?
Problem Statement
現在,給定一個函數\(f(x) = \sum\limits_{k=0}^{n-1} a_k x^k\),請求\((1, f(1)), (\omega_n, f(\omega_n), (\omega_n^2, f(\omega_n^2)) \dots (\omega_n^{n - 1}, f(\omega_n^{n - 1})\)?
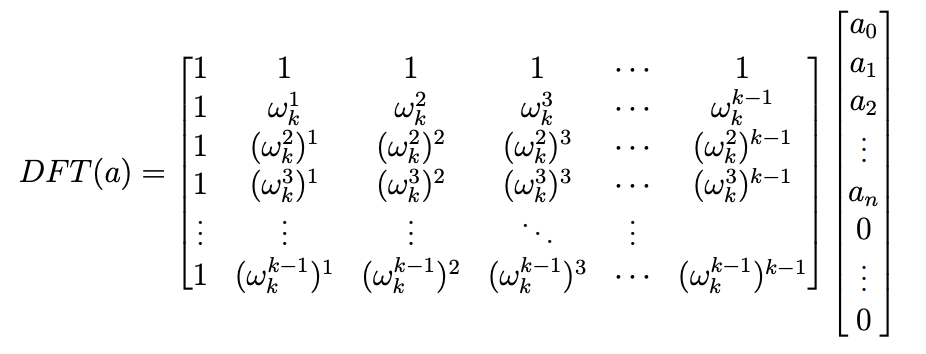
矩陣表示法
以後,我們將假設\(n\)為\(2\)的冪次。若不是,則可以補零到是就好了。
TL;DR:\(n = 2^l\)
Was ist FFT?
\(n \log n\) Speedup
\(f(x) = E(x^2) + xO(x^2)\)
假設\(O(x) = \sum_{k =0} a_{2k+1}x^k\),\(E(x) = \sum_{k =0} a_{2k}x^k\)
Was ist FFT?
\(n \log n\) Speedup
\(f(x) = E(x^2) + xO(x^2)\)
若\(O[k] = O(\omega_{\frac{n}{2}}^{k})\),\(E[k] = E(\omega_{\frac{n}{2}}^{k})\),所求\(f[k] = f(\omega_n^k)\)
遞迴計算的結果
Was ist FFT?
\(n \log n\) Speedup
Was ist FFT?
\(n \log n\) Speedup

Was ist FFT?
And then...
但是...
有了這堆東西...
除了炫耀還能幹嘛啊?
感覺還需要一個東西轉回去⋯⋯
Was ist FFT?
Inverse FFT
還記得FFT有矩陣表示方式嗎:\(A_{ij} = \omega_n^{ij}\) (0 base)
那可以證明,\((A^{-1})_{ij} = \frac{\omega_n^{-ij}}{n}\)哦!
(\(i\neq j\)的時候是和為0的等比級數)
const double PI = acos(-1);
typedef complex<double> cd;
vector<cd> FFT(const vector<cd> &F, bool inv) { // assume F.size() == 2^k
if(F.size() == 1) return F; // base case (important)
vector<cd> rec[2];
for(int i = 0; i < F.size(); i++) rec[i&1].push_back(F[i]);
rec[0] = FFT(rec[0],inv);
rec[1] = FFT(rec[1],inv);
double theta = (inv ? 1 : -1) * 2 * PI / F.size();
cd now = 1, omega(cos(theta), sin(theta));
vector<cd> ans(F.size());
for(int i = 0; i < F.size()/2; i++) {
ans[i] = rec[0][i] + now * rec[1][i];
ans[i+F.size()/2] = rec[0][i] - now * rec[1][i];
now *= omega;
}
if(inv) for(int i = 0; i < ans.size(); i++) ans[i] /= 2;
return ans;
}註:為求效率,也可以寫成迴圈版本,避免遞迴
const double PI = acos(-1);
typedef complex<double> cd;
void FFT(cd F[], int n, bool inv) { // in-place FFT, also assume n = 2^k
for(int i = 0, j = 0; i < n; i++) {
if(i < j) swap(F[i], F[j]);
// magic! (maintain j to be the bit reverse of i)
for(int k = n>>1; (j^=k) < k; k>>=1);
}
for(int step = 1; step < n; step <<= 1) {
double theta = (inv ? 1 : -1) * PI / step;
cd omega(cos(theta), sin(theta));
for(int i = 0; i < n; i += step*2) {
cd now(1,0);
for(int j = 0; j < step; j++) {
cd a = F[i+j];
cd b = F[i+j+step] * now;
F[i+j] = a+b;
F[i+j+step] = a-b;
now *= omega;
}
}
}
if(inv) for(int i = 0; i < n; i++) F[i] /= n;
}扣的
power
Implement an operation that is equivalent to the operation \(DFT^P\), where \(DFT\) is the discrete Fourier transform.
一種方法是先取ln,乘上倍數後再exp
另一種方法則是
inverse
牛頓逼近法
結論:
division and modulo
結論:
\(A(x) = B(x)Q(x) + R(x)\)
設\(n = \deg A \geq m = \deg B\)
則\(\deg Q = n-m, \deg R < m\)
ln, exp, sqrt, etc...
其他生成函數
當你想要考慮物件的順序的時候可以考慮「指數生成函數」
光維基上神奇的生成函數就好多 OAO
例如什麼跟數論函數有關的Lambert、Dirichlet之類的
理論上只要保證解析函數 \(\mu_k(x)\)線性獨立
\(\sum_{k=0}^\infty a_k \mu_k(x)\) 應該都可以拿來用吧(?)
例如 \(\mu_k(x) = \cos(kx)\) 之類的
以上言論若有錯誤不負責
指數生成函數的乘法
取數個物品A和物品B,共取n個
排列順序不同算不同方式的方法數
Example
考慮一個排列 \(p\),令 \(f(p)\) 表示每次操作可以交換任意兩個數字的位置時,排序好這個排列所需要的最少次數
對於 \(i = 1, 2, \dots, n\)
求有多少種排列使得 \(|p|=i, f(p) = i-2\)
Example
可以知道題目就是要求有兩個環的排列
我們先考慮恰是一個環的排列,有 \((n-1)!\) 種方法數
那麼從 \(n\) 個元素裡面選出 \(k\) 個分給第一個環,另外 \(n-k\)個分給第二個環,也就是
\[\sum_k \binom{n}{k}(k-1)! (n-k-1)!\]
令 \(\displaystyle F = \sum_{k=0}^n (k-1)! \frac{x^k}{k!}\)
所求就是 \(\frac{1}{2}F^2\)
推廣
- 恰好有 \(k\) 個環?
- 環的個數介在 \(L, R\)之間?
Common Series
習題(或例題)QQ
連講師都不會
- 對於⼀個集合 \(S\),定義 \(f_S(n)\) 為將 \(n\) 寫成 \(S\) 裡⾯的元素的和的⽅法數(元素可重複)。
給定 \(n, p\),請求出 \(f_S(1), f_S(2), \dots, f_S(n)\)模 \(p\) 的餘數。 - 對於一個長為 \(n−2\) 的序列,元素為 \([1,n]\) 中的整數,且出現次數最多的元素出現 \(m−1\) 次,求不同的序列個數。\(n, m \leq 5 \times 10^4\)
- 隨機給⼀個⼤⼩為 \(n\) 的有根⼆元樹,試問葉節點個數的期望值
- 隨機給⼀個⼤⼩為 \(n\) 的有根⼆元樹,試問葉節點個數平方的期望值
- 有 \(n\) 顆(不同的)珍珠,⽤ \(D\) 個顏⾊去塗⾊,試問⾄少能湊出 \(m\) 對相同顏色珍珠的⽅法數
- 上面幾題是從AY的講義抄來的,好像其實有OJ不過我懶得列出來
no judge (?)
Fuzzy Search 系列
AGC
其實我也不會 好爽喔

