Useful Tools

\(\TeX?\)

  • TeX是高德納（Donald Knuth）發明的排版系統
  • 據說是因為他在撰寫巨著《電腦程式設計藝術》時對當時的電腦排版不甚滿意，於是決定自行編寫一份排版軟體
  • 其中包含了當時許多其他軟體沒有或者不成熟的功能，例如：數學公式的自動間距調整、特殊的斷字演算法等等

LaTeX & TeX

  • LaTeX是基於TeX的排版系統
  • 什麼意思呢？它們的關係就像是終端機與GUI一樣，TeX的指令較為基本
  • 而LaTeX則包含了將大量指令簡寫的巨集
  • 使用LaTeX也可以直接利用前人編寫的巨集
\trivlist \let \\ \@centercr
\rightskip \@flushglue \leftskip
\@flushglue \parindent \z@ \parfillskip
\z@skip \item\relax
Some text...
\endtrivlist

 

\center
Some text...
\endcenter

LaTeX有什麼用???

  • 清楚表達你喜愛的排版格式
  • 以你的需求選擇適合的巨集
  • 可跨平台編譯（雖然有些微差異）

https://www.csie.ntu.edu.tw/~tzhuan/www/resources/ntu/

複雜的數學公式 OAO

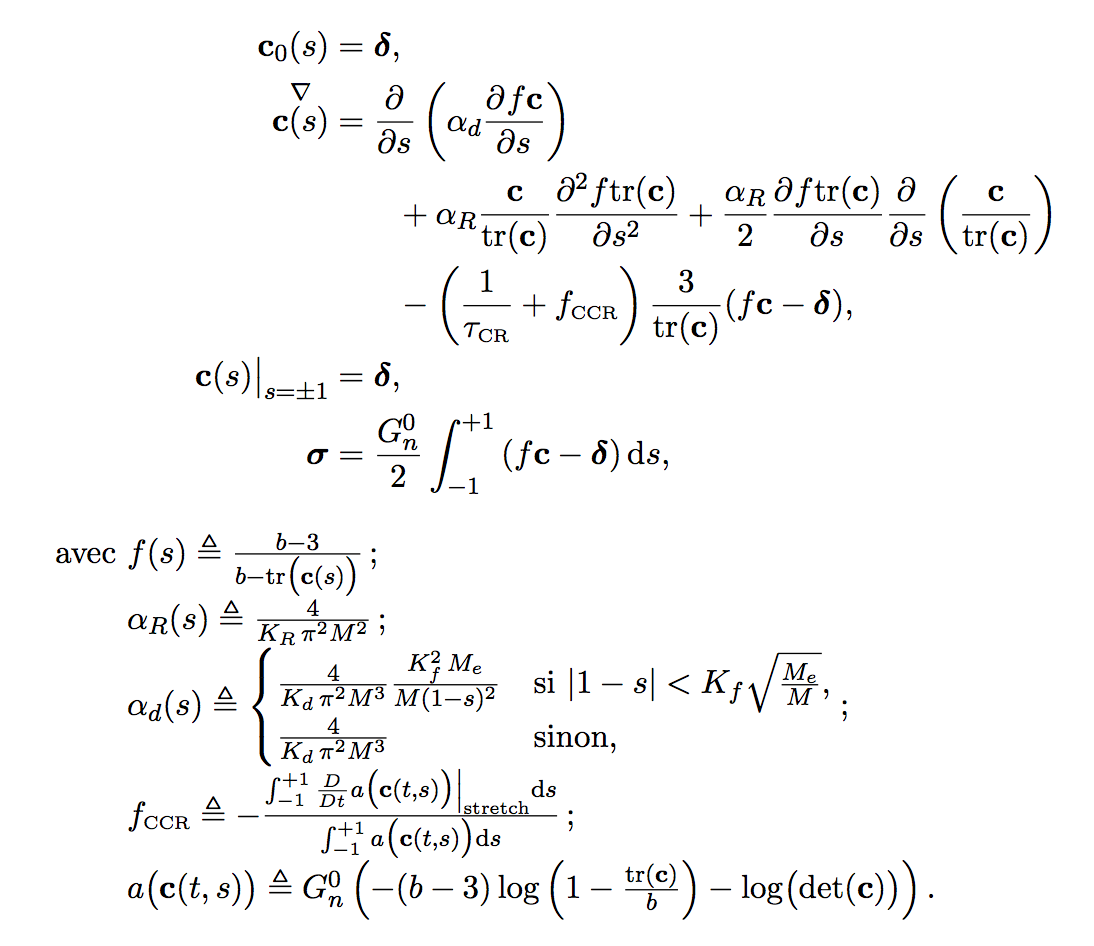
各種奇形怪狀（？）的巨集

https://ctan.org/pkg/

關於唸法 & 寫法...

  • TeX一詞似乎來自於希臘文 τέχνη （TEXNH），意為「藝術」和「製造」，也是 technical 的詞源
  • 故TeX的標準讀法是\(\text{/tɛx/}\)，其中\(\text{/x/}\)相當於「ㄏ」的發音
  • 不過LaTeX的開發者Lamport表示對LaTeX的讀音沒有偏好。
  • 英語系國家多將「 X 」唸為\(\text{/k/}\)

關於唸法 & 寫法...

  • 根據Wiki，TeX系列詞彙的書寫都必須盡量以「\(\TeX\)」的形式呈現，否則必須遵照 T, X 大寫，e 小寫的原則
  • LaTeX則是應盡量寫成\(\LaTeX\)，或者遵照 L, T, X大寫，a, e 小寫的原則，以免和 latex （乳膠）搞混，以及被嘴砲
  • 這份 slides 因為美觀問題還有我偷懶，大部分不會用上述上下標的文字 XD 不要在意細節啦

Math display

Math display

你可能會在各種地方看到這種表示方式...

ax^2+bx+c = 0

x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

\nabla ^{2}f={1 \over r^{2}}{\partial  \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial  \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \phi ^{2}}

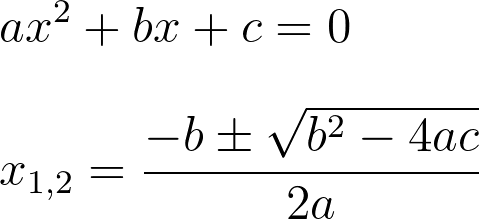
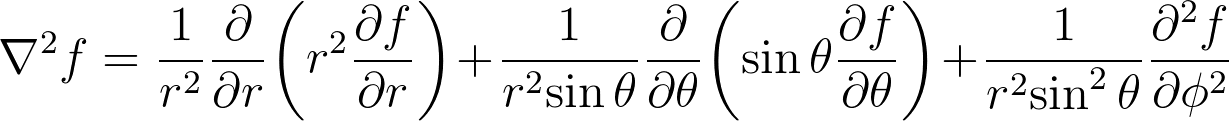
Math display

  • 一般運算子

  • ∠≧∀≦∃

  • 上標、下標

  • 分數、根號

  • 微分、積分

  • 空白、文字

  • 矩陣、列舉

Math display

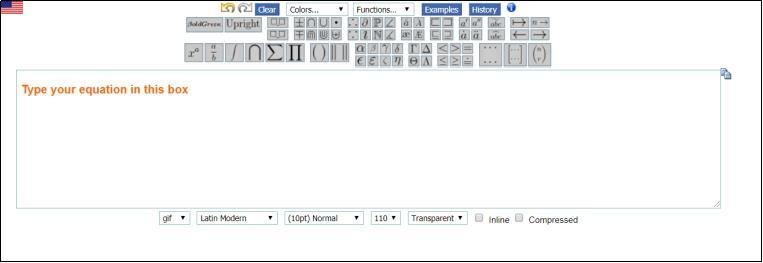
直接在文字方塊中鍵入指令就會顯示在下方，還能下載為圖片！此外也能用上方的按鈕直接選擇你需要的指令或格式，所以其實很多指令都不需要去背。

https://codecogs.com/latex/eqneditor.php

預備知識

  • \(\TeX{}\)以反斜線開頭作為指令的標記，由反斜線後直到非字母的第一個字元被視為調用的指令名稱
  • 之後可以接「可選參數」及「必填參數」，分別以\(\texttt{[], \{\}}\)包住，參數可以是零個也可以很多個。
  • 例如上面的sqrt，\(\texttt{[]}\)裡面的n代表「n次方根」，而\(\texttt{\{\}}\)裡面的x代表根號裡面要放的東西，用\(\texttt{[]}\)包起來的東西通常是可以省略的，在\sqrt{x}的例子中就是沒有小字的根號

\(\LaTeX{}\)指令的格式

\sqrt[n]{x}

預備知識

按鍵在哪裡??

看你自己的鍵盤啦

Math display

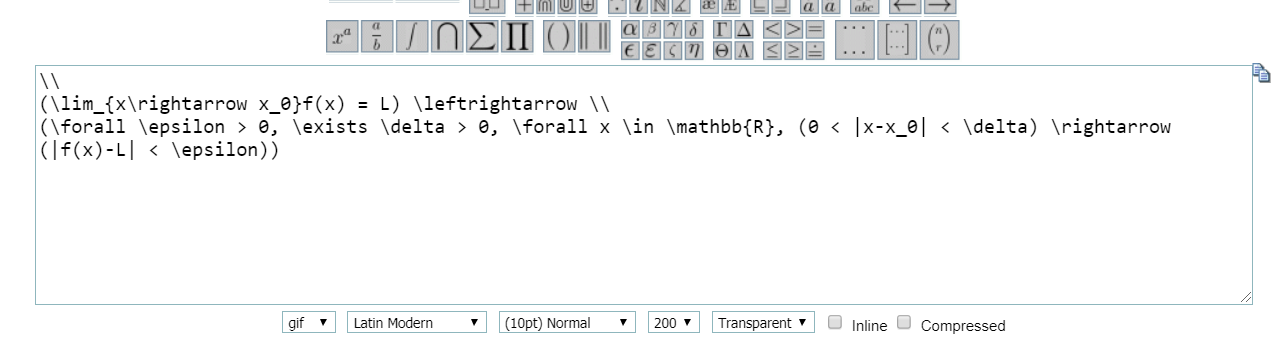
因為 codecogs 的第一行會縮排，若你用到了第二行，文字不會和第一行從同一個起點開始。解決這個問題的一個方法就是直接在第一行換行，如此縮排就會消失。

Math display

下面是部份的基礎指令介紹。

格式 功能 外觀
a_b / a_{p,q} 下標/足標
x^3 / 2^{3+5} 上標/冪次
a \leq b / x \geq y 小於等於、大於等於
a \cdot b ​點乘
a \times b 叉乘
a \div b 除號
\frac{q}{p} 分數
a_b / a_{p,q} \\ x^3 / 2^{3+5} \\ a \leq b / x \geq y \\ a \cdot b \\ a \times b \\ a \div b \\ \frac{q}{p}

Practice

\[\frac{19}{20} = \frac{1}{2} + \frac{1}{3} + \frac{1}{9} + \frac{1}{180}\]

\[2^a \div 2^b = 2^{a-b}\]

\[6\times 6+25\div 5=36+5=41\]

\[(a+b+c)^2 = a^2 + b^2 + c^2 + 2(a \cdot b + b \cdot c + c \cdot a)\]

Math display

格式 功能 外觀
\pm / \mp 加減號
\sqrt[n]{x} 根式
\cdots / \dots 省略號
\because ​因為
\therefore 所以
\sum_{k=1}^n sigma 求和符號
\forall、\exists 對於所有、存在
a b \ c  \\ ​空白、換行
​\text{xyz} ​文字模式
\pm / \mp \\ \sqrt[n]{x} \\ \cdots / \dots \\ \because \\ \therefore \\ \sum_{k=1}^n \\ \forall、\exists \\ a b \ c \\ \text{xyz}

Practice

\[\frac{19}{20} = \frac{1}{2} + \frac{1}{3} + \frac{1}{9} + \frac{1}{180}\]

\[\sum_{k=1}^{n-1} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots + \frac{1}{2^{k-1}} = \frac{2^n-1}{2^{n-1}}\]

\[r={\frac {\sum \limits _{i=1}^{n}(X_{i}-{\overline {X}})(Y_{i}-{\overline {Y}})}{{\sqrt {\sum \limits _{i=1}^{n}(X_{i}-{\overline {X}})^{2}}}{\sqrt {\sum \limits _{i=1}^{n}(Y_{i}-{\overline {Y}})^{2}}}}}\]

\[\frac{1}{n}\sum_{i=1}^n{a_i} \geq \sqrt[n]{\prod_{i=1}^n{a_i}} \geq n\big(\sum_{i=1}^n{\frac{1}{a_i}}\big)^{-1}\]

\[\forall \epsilon >0,\exists N\in \mathbb {N} ,\forall n>N,|x_{n}-L|<\epsilon\]

打指令的時候要注意的東西

  • 不要把反斜線（ \ ）打成斜線（ / ）
  • 括弧要好好配對，例如\(\texttt{[], \{\}, \{\{\{[]\}\}\{\}\}}\)等等
  • 可以常常加空格增加可讀性XD，因為一般的空格會被\(\TeX{}\)忽略
  • 通常\(\texttt{\{\}}\)會接在指令後面表示裡面的內容，例如\frac{q}{p}；但也可以把大括弧中間的東西包成一個「環境」，環境中字體的調整不會影響到環境外，同時整個環境會被環境外的指令視為只有一個字母
  • 例如若想要寫出「a的p+q次方」就必須將p+q用大括弧包起來，寫成a^{p+q}的形式（就像數學裡面的括號，3 x (4 + 5) 中的 4 + 5 會被先算一樣）

但是...安裝好麻煩

\(\KaTeX\)

for websites

Messenger、Wikipedia、...

一些神奇的工具

Markdown

Markdown

Slides!

Slides!

Slides!

  • text
  • image
  • video
  • shape
  • line
  • iframe
  • table
  • code
  • math

Slides!

inline TeX

  • 在slides的text裡面可以使用剛剛學到的math display
  • \(\)和\[\]分別是不同大小和排版的數學模式
  • 例如\[\int{x^2} = \frac{x^2}{3}+C\]顯示為

\[\int{x^2} = \frac{x^2}{3}+C\]

  • 至於\(\int{x^2} = \frac{x^2}{3}+C\)顯示為

\(\int{x^2} = \frac{x^2}{3}+C\)

Made with Slides.com