Math research: all fun and games?

Bjørn Kjos-Hanssen

Department of Mathematics

Math research: all fun and games?

Wherein we try to illustrate by an example what research into pure mathematics is, and how it fits in with teaching of courses and applying for grants

Teaching...

In a small class project for MATH 301 (Discrete Mathematics, taught by Prof. Kjos-Hanssen) in Spring 2009, students studied a notion of automatic complexity of a sequence of zeros and ones.

...via games

Try the Complexity Guessing Game!

currmax = -1
for j in range(0, len(seq)):
	if seq[j]  > currmax + 1: return False
	if seq[j] == currmax + 1: currmax += 1
	if currmax == self.q - 1: return True
return True

Part of pure math research is to work things out with pencil and paper, look up old work, and ponder ideas before/after taking a nap. Another part is sometimes to get computer help.

Python code

The Thue-Morse sequence:

01 10

0110 1001

01101001 10010110

...

In the paper we present new results about how complex it is (found while I was on sabbatical leave at University of Oslo, Norway, in Fall 2013).

Extending results of Shallit and Wang (University of Waterloo, Ontario, Canada, 2001)

0110100110010110...

The Thue-Morse sequence is overlap-free; unlike words like entente, banana, alfalfa

The Thue-Morse sequence appears many places in pure mathematics.

Automatic complexity?

This is a miniature version of the notion of Kolmogorov complexity.
A computer program written by three students in the class calculated the complexity of all such sequences of length at most 7.

The perhaps most interesting finding was that the string 011100 is the only string of length 6 or less whose complexity is increased when read backwards.
That is, 001110 is more complicated than 011100.

Example

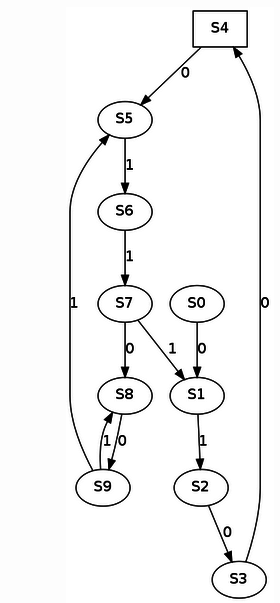
Pictured: a finite state automaton which only accepts one string of length 22, namely 0100011001010101111100, and which has 10 states. We say that this automaton is a witness to the fact that the string 0100011001010101111100 has automatic complexity at most 10.

Grad students

This project was continued by Master’s student Kayleigh Hyde, who graduated in 2013. She presented our joint paper at the International Computing and Combinatorics Conference in Atlanta, Georgia, in August 2014.

Grants

In September 2014 Prof. Kjos-Hanssen was awarded a five-year grant from the Simons Foundation, also entitled “Automatic Complexity”, to continue this research in collaboration with other mathematicians.

This grant is part of the grant program Collaboration Grants for Mathematicians.

Vertical integration

This line of development from 2009 to 2014 is an example of vertical integration of all levels.

From beginning undergraduate work, through graduate theses, to externally funded research.

Application: finance

The Complexity Option Game allows the player to bet on dips in the automatic complexity of a price path.

The corresponding paper, joint with two Financial Engineering Master's graduates and one Math Master's graduate, is under review for the journal Algorithmic Finance.

Application: Statistics

In a new project, Prof. Kjos-Hanssen investigates the use of so-called structure functions for automatic complexity to statistically analyze data. For example, the most statistically significant fact about a string such as 0000000010000000100, from an automatic point of view, may be the fact that it contains exactly two 1s.

The precise number of 0s that occurs may be relatively insignificant. The theory of structure functions makes this intuitive idea precise.