MathML

What elephant?

What about...

"You can already do very good stuff with technologies we have today: SVG, ARIA, modern CSS, JavaScript and so on: including the ability to display accessible formulae from many sources.  One is MathML, but there are others."

• Not untrue... incomplete

• Many good points mixed in the conversation

parts of this problem

• How do you type math?
• Who parses and makes sense of that?
• What do they do with it?
• What can you do with what they do with it?

 

They get incredibly wound up and difficult to discuss....

That's not the proposal.
If it were I think it wouldn't be a very good one...
That seems uncontroversial. If a well specified markup about Math presentation is too verbose or general - how much more so of a general purpose markup (HTML or SVG -- an order of magnitude more?)

What SVG, CSS, ARIA  would you author? Is there a practices rec?

That's not about authoring, that's about rendering.

Could be anything - currently ASCII Math, TeX, and MathML

 

Those can be transformed into those other things.

What would authors write?

<something>f^g \left( f' \frac{g}{f} + g' \ln(f) \right)</something>

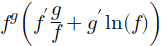
Very interesting, also very different

TeX or ASCII Math

• Parse DOM
• Find a ...?text node
• Parse a text node
• Create a complex DOM from it
  • ​again, what DOM?
• ...? (next slides)
• Profit

Similar to markdown, but markdown has a clear standard mapping.. What is the mapping to SVG or HTML/ARIA/CSS?

When does this transformation happen, and how?

Many possible ways... Each creates their own follow on questions and lack strict definitions.

Before it is sent to the browser?

Ecosystems and workflows abundant:

• library per language? (JavaScript, Java, PHP, Ruby, etc) 
• Adapters per use? (Build time, request time)?
• Per framework? (Struts, Spring MVC, JSF, GWT... etc?)

Again, even if they all existed already (they don't afaik) what standard do they apply? Given the same input, shouldn't they produce the same output?

After it is sent to the browser?

When? What does the waterfall look like? FOUC? When is it 'ready'? What is the lifecycle?

How? What standard does it apply?

 

And, at the end of the day...

Wait..This is not my tree?

The way that all reasoning about things happens in the browsers is through the DOM tree - whether that is JavaScript or CSS or even XSL... and this is not the tree that the author created.

Or, at some point it was, and now it isn't?

 

Or, it is, but it isn't?

 

Or, it is, but it is more?  At some point?  

1. Interesting ideas!
2. Good points (will explain more)!
3. Introduces many new questions, needs more."  So many moving parts/variables.
   
   Vague, but exciting.

Ack good points (kind 1)

• MathML is verbose
• Despite this, it is not particularly semantic
• We should be exploring the future in other ways

Ack good points (kind 1)

• It is verbose
  • in the same way all HTML is historically
  • actual DOM created alternatively is more so
• Despite this, it is not particularly semantic
  • in the same way all HTML is historically
  • We should work on that regardless - that belongs elsewhere (ARIA/AOM)
• We should be exploring the future in other ways
  • Yes, and we'd like to make this even more plausible. What we disagree on is an approach and starting point.

Why MathML then?

• Very practical reasons
  • Mature ecosystem, existing content
  • It uses the language of the DOM
    • Every browser supports parsing it interoperably
    • It probably ultimately needs a tree.
    • This is your tree.  
  • Support in 2 of 3 rendering engines currently
    • Some not insignificant support already in chromium
  • Can help us get to better
• Historical meta-point about standards, communities and what's important.

 

What if we had this \int_0^{\pi} 2 \cos(\theta) - 3 \sin(\theta) d\theta =

\left[ 2 \sin(\theta) + 3 \cos(\theta) \right]_{\theta=0}^\pi = -6 in our HTML?

 

 

What if we had this $\int_0^{\pi} 2 \cos(\theta) - 3 \sin(\theta) d\theta =

\left[ 2 \sin(\theta) + 3 \cos(\theta) \right]_{\theta=0}^\pi = -6$ in our HTML?

 

Wait, surround it by $$? How do we know?

Basically, we have to answer all of those questions:

 

• How do we know there is some content
• ...In the text somewhere
• .. that could appear at any time
• ...and that it is LaTeX
• ...and specifically this, and parse it
• ...and then display it
• ...and ideally give authors a way to  use it as they would anything else in the platform

Or we use the platform, we plug into the lifecycle...

 

<p>What if we had this <x-tex>

\int_0^{\pi} 2 \cos(\theta) - 3 \sin(\theta) d\theta =

\left[ 2 \sin(\theta) + 3 \cos(\theta) \right]_{\theta=0}^\pi = -6

</x-tex> in our HTML?</p>

MathJaX could do this part too...

These are separable problems, they just aren't often discussed as such.

Importantly though, if we use the platform to render mathy stuff, without destroying your tree, and with a clear mapping...

 

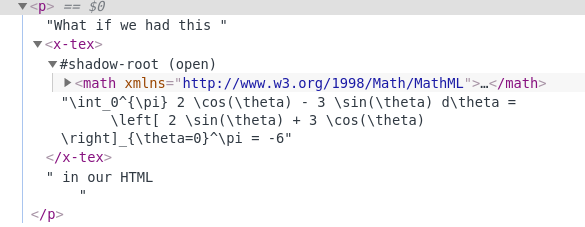
There are so few moving parts!
Moving parts and variables create complexity and cost money.

Can we standardize that?

 

Maybe?  There's no precedent, but having fewer moving parts and questionable things seems to help the prospects.

Or ascii math, if you prefer...

What's all is happening...

Minimum Viable
Thing, modernized, with feedback in mind.

MathML 3: 

• 195 elements
• 152 attributes
• Lots of new magic

... dictionary editors...

MathML-Core: 

• 25 elements
• Small number of attributes
  • Some deprecated
    • specified mappings to CSS
• Minimal (hopefully 0) new magic itself
  • Lots of examples of ok simplification here

Individual browser tests being migrated to WPT

 

New tests being added

 

Interop improvements

Implementation!

 

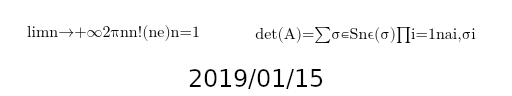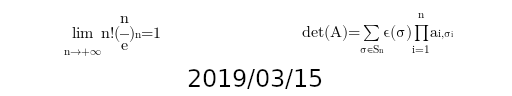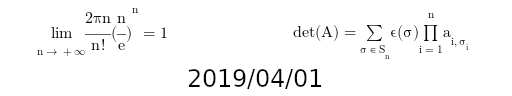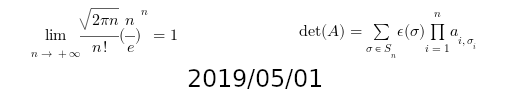
Modern spec format/tools links tests

 

Actually specifies things, and in modern ways

 

IDL!!!

Wait, what?

>  function Element() {
    [native code]
   } 

Wait, what?

>  TypeError: undefined is not an object (evaluating 'el.style.color = 'blue'')

Many of these are things that are good for everyone, regardless of position

 

 

Make MathML less special