建國中學
\(111^{\text{st}}\) 地球科學能力競賽校隊小圈圈
海洋物理學
Presenter: 22527 Brine
昨天才開始做的簡報你在期待什麼東西
Coriolis force
看我能不能默出他的證明
科氏力證明
看到這頁就代表我又忘了
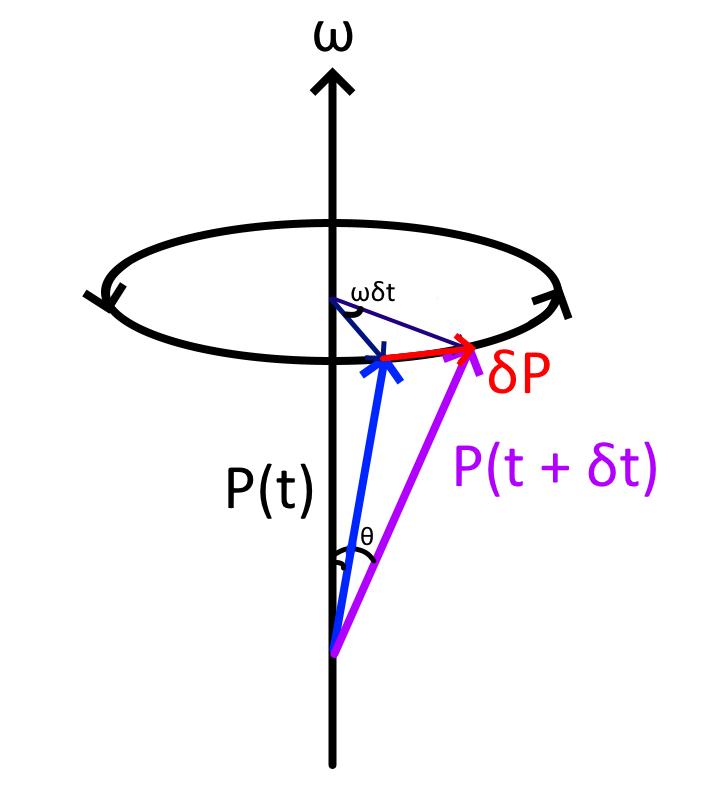
科氏力證明

\frac{Dr}{Dt} = \omega \times r + v
\frac{D^2r}{Dt^2} = \omega \times \frac{Dr}{Dt} + \frac{Dv}{Dt}
\frac{DP}{Dt} = \omega \times P + \frac{dP}{dt}
\frac{D^2r}{Dt^2} = \omega \times (\omega \times r + v) + \omega \times v + \frac{dv}{dt}
A = \frac{dv}{dt} + 2 \omega \times v + \omega^2r
看到這頁就代表我又忘了
渦度 vorticity
你可以不要再找數學來荼毒自己了嗎
什麼是渦度
- \(\zeta, \text{zeta}\)
- 用來描述速度場的旋度
- \(\vec \zeta = \nabla \times \vec v\)
- 有時寫成 \(\vec \omega = \nabla \times \vec u\)
- 蛤
場
- 很多點,每個點都有一個向量
- 速度場(風場)

什麼是旋度?
- 描述一個系統旋轉的工具
\nabla = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z})
\vec v = (u, v, w)
\vec \zeta = (\frac{\partial w}{\partial y} - \frac{\partial v}{\partial z},
\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x},
\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y})
\because w \approx \frac{\partial u}{\partial z} \approx \frac{\partial v}{\partial z} \approx 0
\therefore \vec \zeta = (0, 0,
\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y})
\leftrightarrow |\vec \zeta| = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
什麼意思
- 兩邊差越大就越明顯
\frac{\partial v}{\partial x}
\frac{\partial u}{\partial y}
完整的渦度
- 剛剛討論的是在靜止參考係下的渦度
- 又被稱為「相對渦度」
- 那什麼才是「絕對渦度呢」
- 把轉動座標系造成的影響考慮進去
- 我們知道他是誰嗎?
- 我們的老熟人,科氏參數!
- \(f = 2 \Omega \sin \phi\)
- 絕對渦度 \(= f + \zeta\)
- 位渦守恆
- 可以用來預測流體運動性質
\frac{f + \zeta}{h} = const
潮汐能 Tidal energy
看起來超像永動機,但它不是
不完美的潮汐
- 理論上,月球到哪,滿潮就該到哪
- 但顯然不是這樣的
- 海洋運動需要時間
- 白赤交角 \(23.5^\circ \pm 5^\circ\)
- 地球形狀非球體
- 產生潮汐阻力
- 給地球帶來負的角加速度 \(\omega\)
- \(\approx \text{2.4 ms / 100 years}\)
角動量守恆推導
- \(I\omega = const\)
- 地球質量、轉動慣量、角速度
- \(M, I_M, \omega_M\)
- 月球質量、轉動慣量、角速度
- \(m, I_m, \omega_m\)
- 地月連心距 \(L\)
- 地心—系統質心距 \(d_M=\frac{m}{M+m}L\)
- 月心—系統質心距 \(d_m=\frac{M}{M+m}L\)
I_M \omega_M + I_m \omega_m + M d_M^2 \omega_m + m d_m^2 \omega_m = const
角動量守恆推導
I_M \omega_M + I_m \omega_m + M d_M^2 \omega_m + m d_m^2 \omega_m = const
I_M \omega_M + M (\frac{m}{M+m}L)^2 \omega_m + m (\frac{M}{M+m}L)^2 \omega_m = const
I_M \omega_M + \frac{M + m}{(M+m)^2}Mm \omega_mL^2 = const
I_M \omega_M + \frac{Mm}{M+m} \omega_mL^2 = const
角動量守恆推導
I_M \omega_M + \frac{Mm}{M+m} \omega_mL^2 = const
\(\because\) 地球重力提供月球繞質心運動向心力
\frac{GMm}{L^2} = md_m\omega_m^2 = m\omega_m^2L\frac{M}{M+m}
\frac{G}{L^2}= L\frac{\omega_m^2}{M+m}
\omega_m^2 L^3 = G(M+m)
\omega_m^2 L^4 = G(M+m)L
\omega_m L^2 = \sqrt{G(M+m)L}
角動量守恆推導
I_M \omega_M + \frac{Mm}{M+m} \omega_mL^2 = const
\omega_m L^2 = \sqrt{G(M+m)L}
I_M \omega_M + \frac{Mm}{\sqrt{M+m}} \sqrt{GL} = const
\(\because \frac{d\omega}{dt} < 0\)
\(\therefore \frac{dL}{dt} > 0\)