建國中學
暑假地球科學讀書會
大氣動力學
Presenter: 12527 鄭竣陽
Index
Forces
- pressure gradient force, PGF
- gravitational force
- viscosity
- friction
apparent Forces
- aka pseudo force
- centrifugal force
- coriolis force
whiteboard time
Drawing on computer is hard. Have mercy on me.
Pressure gradient force
- assume there's an air parcel
a_x = -\frac{1}{\rho}\frac{\partial P}{\partial x\ }
a_y = -\frac{1}{\rho}\frac{\partial P}{\partial y\ }
a_z = -\frac{1}{\rho}\frac{\partial P}{\partial z\ }
Gravitational force
\vec{F_g} = \frac{GMm}{r^2}(\frac{\vec r}{r})
\frac{\vec{F_g}}{m} = \frac{GM}{r^2}(\frac{\vec r}{r}) \equiv g^*
Viscosity
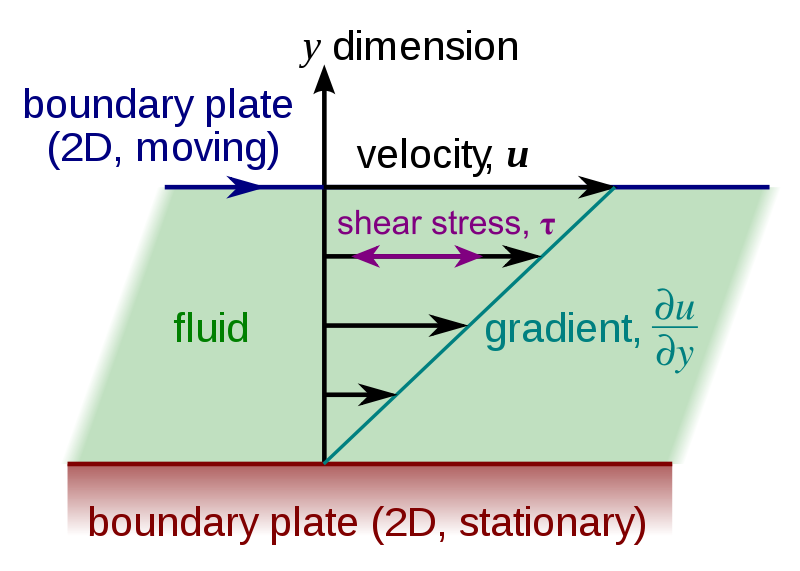
x is parrallel to the line of latitude
y is parralel to the line of longitude
z is the altitude
\dot x \leftrightarrow u \\
\dot y \leftrightarrow v \\
\dot z \leftrightarrow w
F = \mu A \frac{\Delta u}{\Delta z}
(observed)
\tau_{z \to x} = \large \frac{F}{A} \normalsize = \mu \large \frac{\partial u}{\partial z}
Centrifugal Force
\vec g = \vec{g^*} + \Omega^2 \vec R
Viscosity
a_{z \to x} = \frac{(\tau_u - \tau_d)\Delta zA \\}{m}
\\ = \frac{\frac{\partial}{\partial z} \tau_{z \to x} \Delta x \Delta y \Delta z}{m}
\\ = \frac{1}{\rho} \frac{\partial}{\partial z} \tau_{z \to x}
\\ = \frac{\mu}{\rho} \frac{\partial}{\partial z} \frac{\partial u}{\partial z}
\\ = \nu \frac{\partial^2 u}{\partial z^2}
a_x = a_{x \to x} + a_{y \to x} + a_{z \to x}
= \nu [\frac{\partial^2 u}{\partial x} + \frac{\partial^2 u}{\partial y} + \frac{\partial^2 u}{\partial z}]
= \nu \nabla^2 u
\nabla = \displaystyle
\sum_{i=1}^n \vec e_i {\partial \over \partial x_i} = \left({\partial \over \partial x_1}, \ldots, {\partial \over \partial x_n} \right)