All models are wrong

Testing your assumptions

Dr. Ben Mather

EarthByte Group

University of Sydney

@BenRMather

Essentially, all models are wrong,
but some are useful.

 

 

- Box & Draper

Empirical Model-Building and Response Surfaces (1987)

@BenRMather

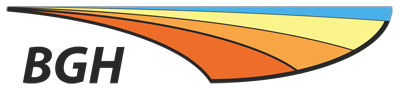
A Newspoll conducted shortly before the federal election predicted a Labor victory 53% to the Coalition's 47% on a two-party preferred preference

@BenRMather

After election night

When it comes to the opinion polling, something’s obviously gone really crook with the sampling
both internally and externally.

- ABC political editor Andrew Probyn

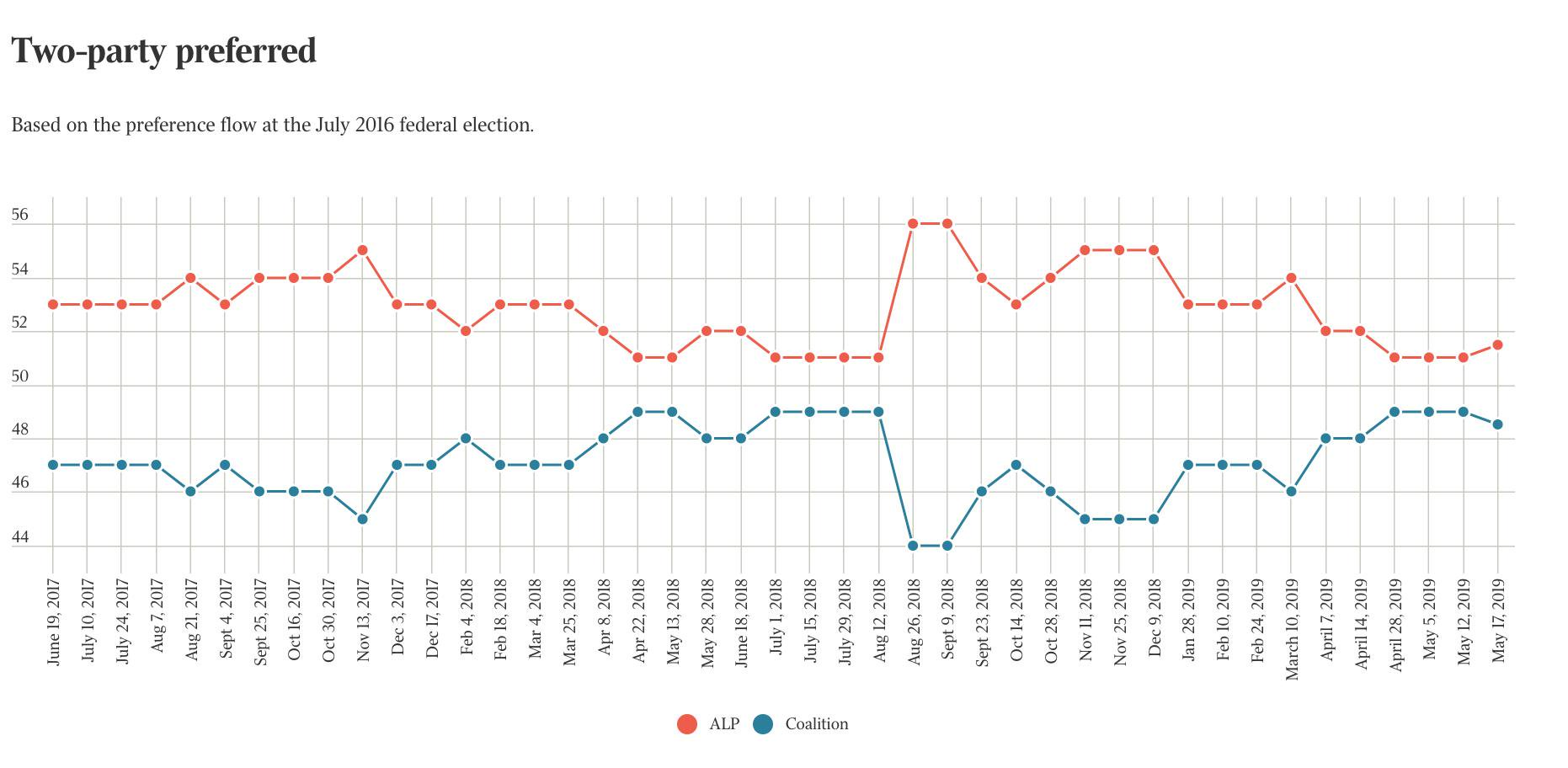
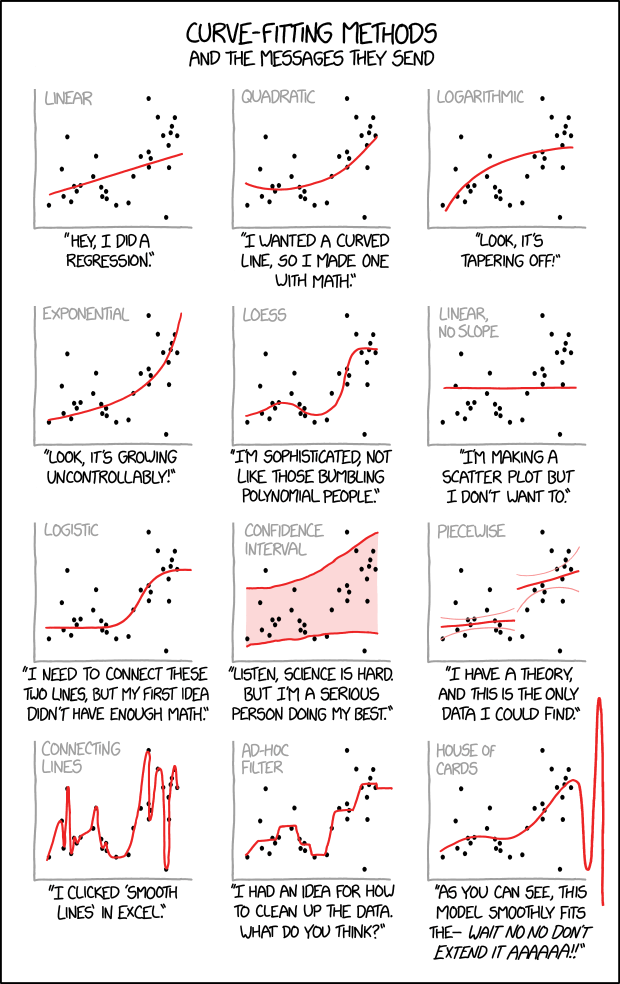
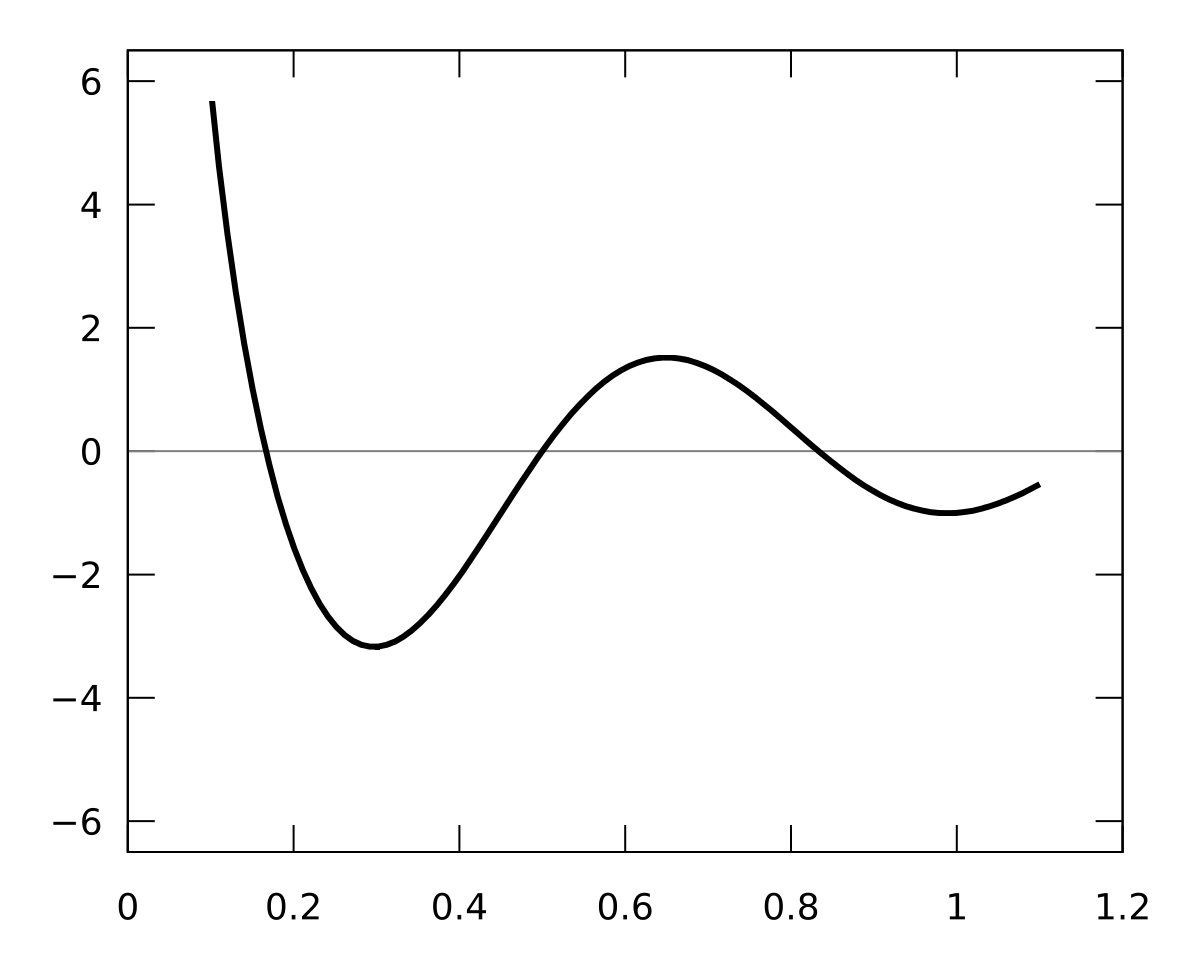
Example:

Line of best fit

  • Linear?
  • Quadratic?
  • Sinusoidal?

@BenRMather

When do we make assumptions?

  • Everyday life
  • Whenever we interpret data
  • When we predict something based on data

@BenRMather

What assumptions?

  • Nature of trends
    • Constant, linear, quadratic, etc.
    • Correlation length scales
  • Distinct populations in data
    • Socio-economic classes, smokers
    • geochemists, palaeontologists, flat earthers
  • Presence of bias in a sample group
    • People who respond to Newspoll surveys
  • When we predict something based on prior experience

Good scientists will...

  1. Make an objective observation.
  2. Infer something (a hypothesis) from that observation.

@BenRMather

Good scientists will not...

  1. Formulate a hypothesis
  2. Find / assume all data that fits their hypothesis

@BenRMather

Some useful assumptions

  • Newton's 3 laws of motion
  • Greenhouse effect
  • The first dice-roll has no effect on the second dice-roll
  • The temperature in Newtown is the same as that in Marrickville
  • John Farnham will perform at least one more goodbye tour

@BenRMather

BIG DATA

There are a lot of words here and most of them mean the same things.

Machine Learning = Inference

Start with the basics

  • Does it pass the common sense test?
  • "Bad" models can also tell you something interesting.
  • Are there alternatives?
  • What are you going to do with your model?

@BenRMather

Generate 50%, 95%, 99% confidence intervals using randomly drawn models

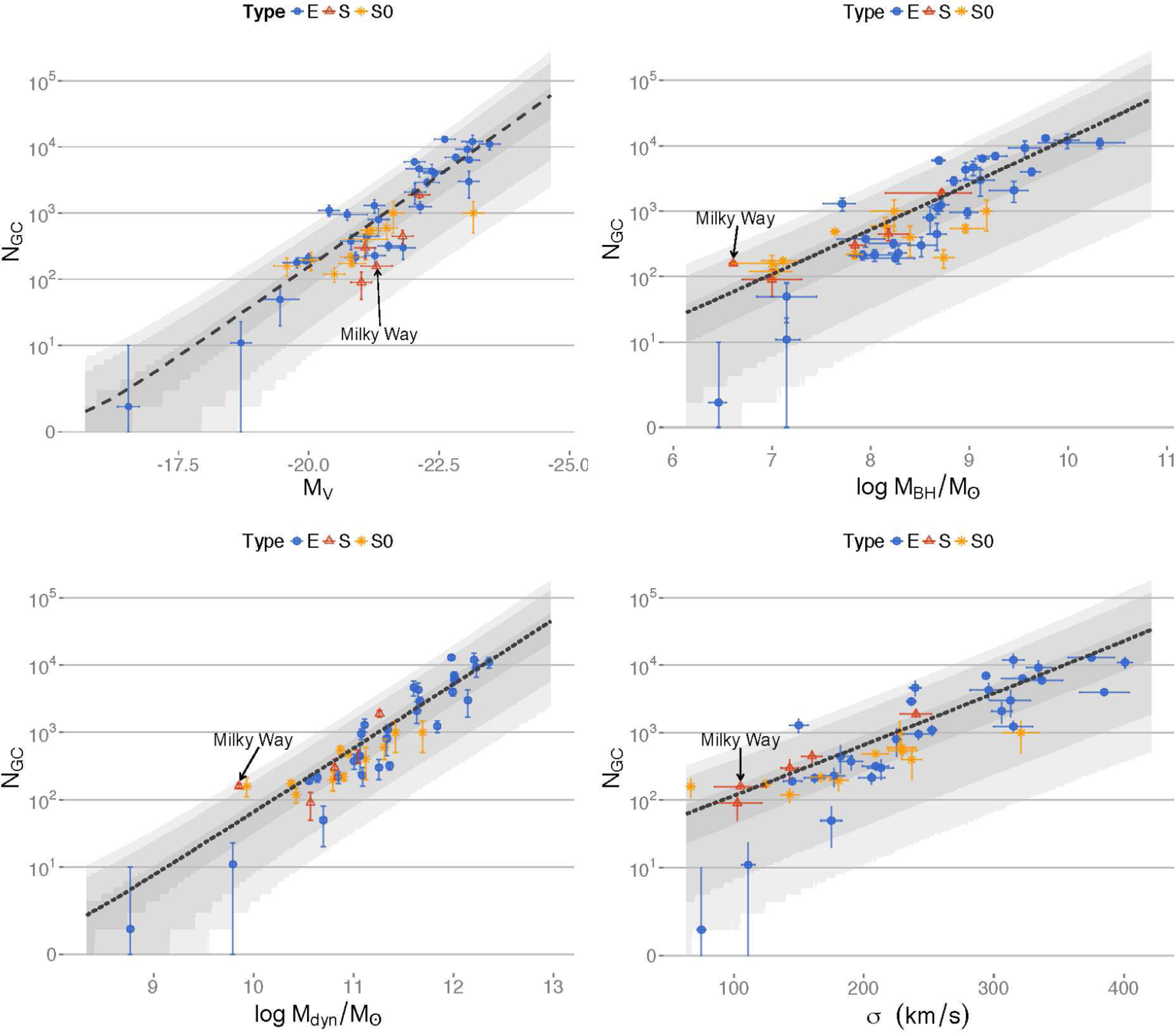
Non-uniqueness

There may be many solutions that fit the same set of observations.

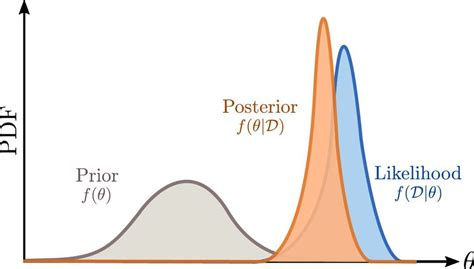
Bayes Theorem

  • Formally describes the link between observations, model, & prior information.
  • Where these intersect is called the posterior
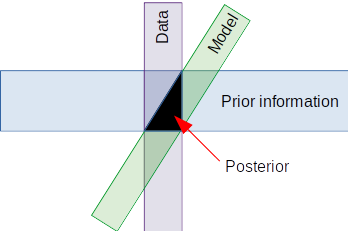
P(\mathbf{m}|\mathbf{d}) \propto P(\mathbf{d}|\mathbf{m}) \cdot P(\mathbf{m})

posterior

likelihood

prior

model

data

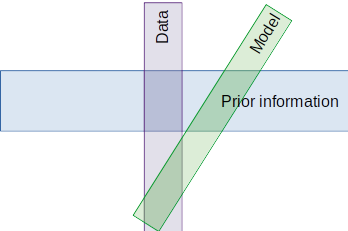
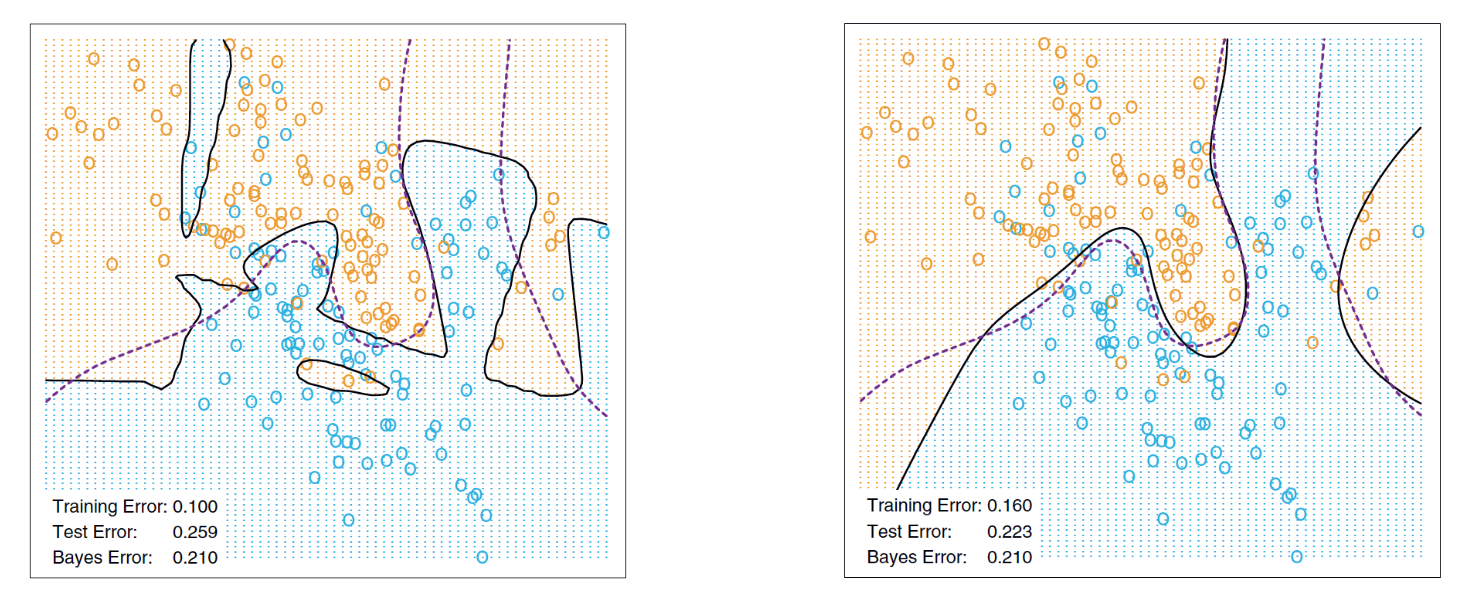
example of an ill-posed problem

@BenRMather

example of a well-posed problem

Data-driven

  • Use the data to "drive" the model.
  • Infer what input parameters you need to satisfy your data and prior information

Input parameters

Model being solved

Compare data & priors

\mathbf{m} : [H_1,H_2,H_3,\ldots, H_n]
\nabla ( k \nabla T) =-H
P(\mathbf{m}|\mathbf{d}) \propto P(\mathbf{d}|\mathbf{m}) \cdot P(\mathbf{m})

FORWARD MODEL

Prior

P(\mathbf{m})

Likelihood

P(\mathbf{d}|\mathbf{m})

Posterior

P(\mathbf{m}|\mathbf{d})

Inverse Model

Sampling

We can estimate the value of pi     with monte carlo sampling.

from random import random

n = int(input("Enter number of darts"))
c = 0
for i in range(n):
    x = 2*random()-1
    y = 2*random()-1
    if x*x + y*y <= 1:
        c += 1
print("Pi is {}".format(4.0*c/n))
\pi

Python code to run simulation

Global
minimum

Local
maximum

Local
minimum

Monte Carlo sampling

Global
minimum

Local
maximum

Local
minimum

Markov-Chain Monte Carlo sampling (MCMC)

Global
minimum

Local
maximum

Local
minimum

MCMC with gradient

Global
minimum

Local
maximum

Local
minimum

MCMC with gradient (caveat emptor!)

trapped!

Heat flow data

  • Assimilate heat flow data

 

  • Vary rates of heat production and geometry of each layer to match data

 

  • Plug m and d into Bayes' theorem
P(\mathbf{m}|\mathbf{d}) \propto P(\mathbf{d}|\mathbf{m}) \cdot P(\mathbf{m})
\mathbf{d} = q_s
\mathbf{m} = [H_1, H_2, H_3, z_1, z_2, z_3]

Heat flow in Ireland

Tectonic reconstructions

  • Ascertain the difference between reconstructions
  • Does not take into account data uncertainty
    • Sensitivity analysis / "bootstrapping"

There are known knowns;

there are things we know we know.

We also know there are known unknowns; that is to say we know there are some things we do not know.

But there are also unknown unknowns - the ones we don't know we don't know.


- Donald Rumsfeld
Former US Secretary of Defense

@BenRMather

Black swans

  • Europeans thought all swans were white... until they came to Australia
  • How can you ever model what you can't imagine?
  • How can you test assumptions without rare events that prove them wrong?

@BenRMather

Thank you

Dr. Ben Mather

Madsen Building, School of Geosciences,

The University of Sydney, NSW 2006

https://benmather.info

www.slides.com/brmather/gesss-2019