Reducing the uncertainty of lithospheric thermal structure

integrated modelling from geothermal, magnetic, and seismic data

Dr. Ben Mather

EarthByte Group & Sydney Informatics Hub

Motivation

Understanding temperature in the crust can help to interpret:

  • hydrocarbon maturity
  • geothermal potential
  • seismic velocity

 

Quantifying its uncertainty is important to estimate the risk associated with a resource

Bayesian Inference

P(\mathbf{m}|\mathbf{d}) \propto P(\mathbf{d}|\mathbf{m}) \cdot P(\mathbf{m})
P(m∣d)∝P(d∣m)⋅P(m)P(\mathbf{m}|\mathbf{d}) \propto P(\mathbf{d}|\mathbf{m}) \cdot P(\mathbf{m})

Posterior  ~  likelihood x prior

P(\mathbf{m}|\mathbf{d}) = A \exp (-S(\mathbf{m}))
P(m∣d)=Aexp⁡(−S(m))P(\mathbf{m}|\mathbf{d}) = A \exp (-S(\mathbf{m}))
S(\mathbf{m}) = \sum_i \frac{\lvert g^i(\mathbf{m}) - \mathrm{d}^i \lvert^2}{(2\sigma_{\mathrm{d}}^i)^2} + \sum_{j} \frac{\vert \mathrm{m}^j - \mathrm{m}^j_p \vert^2}{(2\sigma^j_p)^2}
S(m)=∑i∣gi(m)−di∣2(2σdi)2+∑j∣mj−mpj∣2(2σpj)2S(\mathbf{m}) = \sum_i \frac{\lvert g^i(\mathbf{m}) - \mathrm{d}^i \lvert^2}{(2\sigma_{\mathrm{d}}^i)^2} + \sum_{j} \frac{\vert \mathrm{m}^j - \mathrm{m}^j_p \vert^2}{(2\sigma^j_p)^2}

-norm objective function

l_2
l2l_2
  • Bayes theorem describes the posterior as the probability of a model given the data

 

 

  • The posterior probability can be evaluated with an objective function

 

  • We seek the maximum a posteriori (MAP) model, which can be obtained by minimising S(m).

Adjoint inversion

Efficiently invert a large number of parameters

Added complexity to compute forward problem AND gradient vectors

Entrapment by local minima

Number of evaluations increase exponentially with dimensions

Copes better with highly nonlinear problems

Posterior distribution

MCMC

Adjoint

+

+

+

-

-

-

Thermal solver

\nabla(\mathbf{k} \nabla \mathbf{T}) = - \mathbf{H}
∇(k∇T)=−H\nabla(\mathbf{k} \nabla \mathbf{T}) = - \mathbf{H}

Objective function

S(\mathbf{m}) = \sum_i \frac{\lvert g^i(\mathbf{m}) - \mathrm{d}^i \lvert^2}{(2\sigma_{\mathrm{d}}^i)^2} + \sum_{j} \frac{\vert \mathrm{m}^j - \mathrm{m}^j_p \vert^2}{(2\sigma^j_p)^2}
S(m)=∑i∣gi(m)−di∣2(2σdi)2+∑j∣mj−mpj∣2(2σpj)2S(\mathbf{m}) = \sum_i \frac{\lvert g^i(\mathbf{m}) - \mathrm{d}^i \lvert^2}{(2\sigma_{\mathrm{d}}^i)^2} + \sum_{j} \frac{\vert \mathrm{m}^j - \mathrm{m}^j_p \vert^2}{(2\sigma^j_p)^2}
\mathbf{x}: [k_1, k_2,\ldots, k_n, \\ H_1, H_2,\ldots, H_n ]
x:[k1,k2,…,kn,H1,H2,…,Hn]\mathbf{x}: [k_1, k_2,\ldots, k_n, \\ H_1, H_2,\ldots, H_n ]

Input parameters

Forward

Model

Adjoint

Model

Gradient descent

The gradient descent method for finding successibely better approximations to the minimum of S(m) is:

\mathbf{m}_{i+1} = \mathbf{m}_i - \mu \nabla S(\mathbf{m}_i)
mi+1=mi−μ∇S(mi)\mathbf{m}_{i+1} = \mathbf{m}_i - \mu \nabla S(\mathbf{m}_i)

However, we use a quasi-Newton nonlinear solver to approximate the Hessian (2nd derivatives)

  • Useful because the Hessian is difficult to compute

Regional context

SE Australia is an accretionary terrane combining Proterozoic and Phanerozoic crust

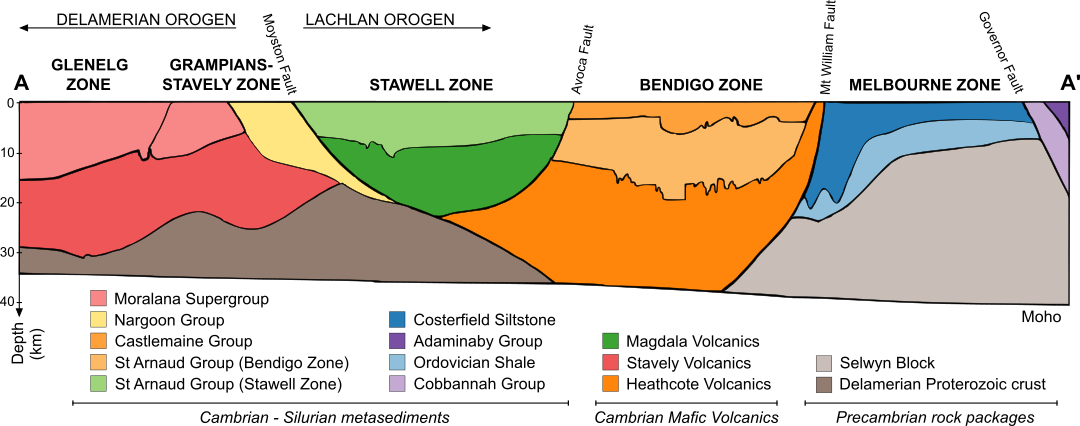
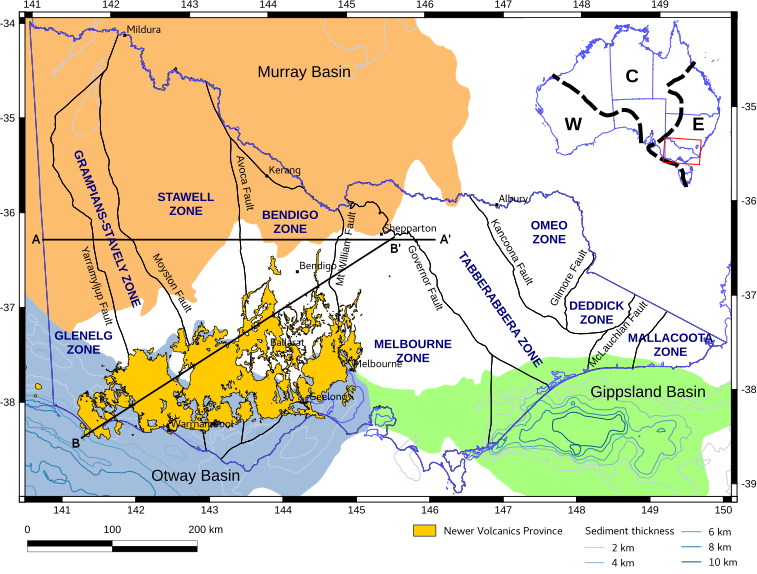
A

A'

Data assimilation

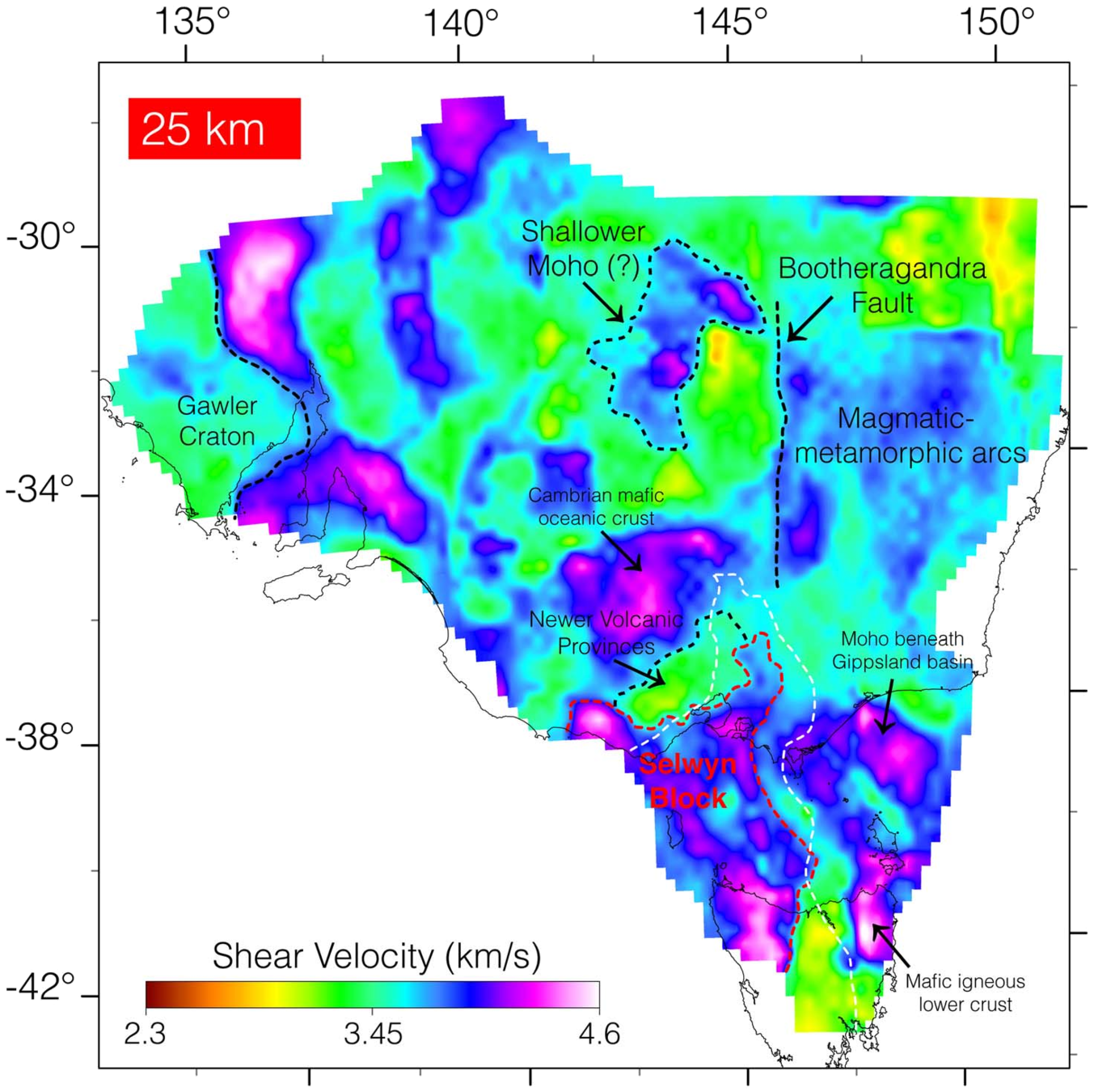
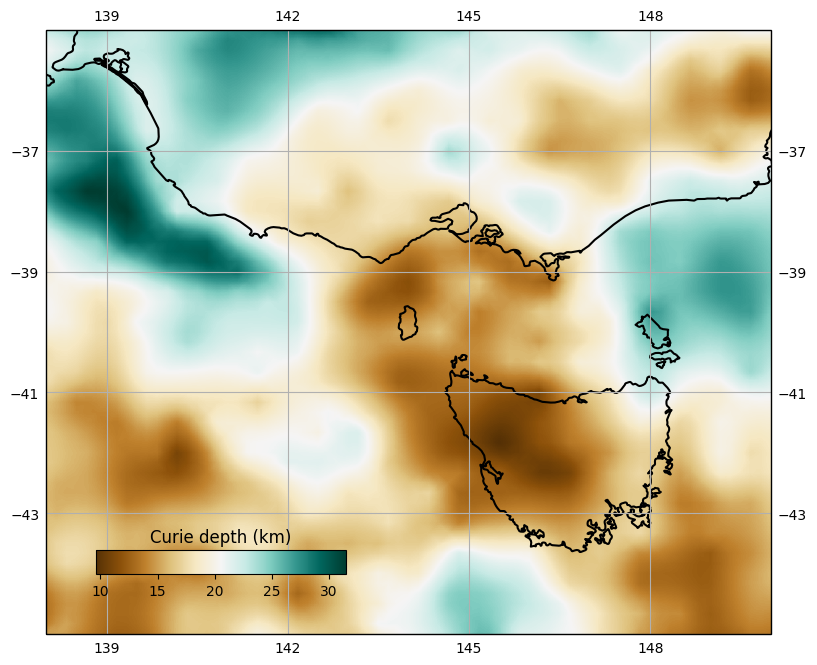
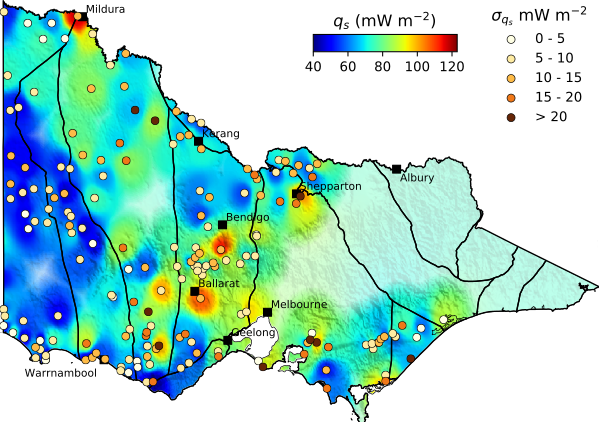
  • On their own, any of these datasets result in non-unique solutions of temperature.
  • Together, they constrain temperature in the lithosphere to a reasonable degree of uncertainty.

HEAT FLOW

CURIE DEPTH

SHEAR VELOCITY

Uncertainty reduction

Coupling gradient inversion with local sampling builds an approximation of the posterior

  1. Perturb observation within PDF
  2. Perturb priors within PDF
  3. Build the ensemble
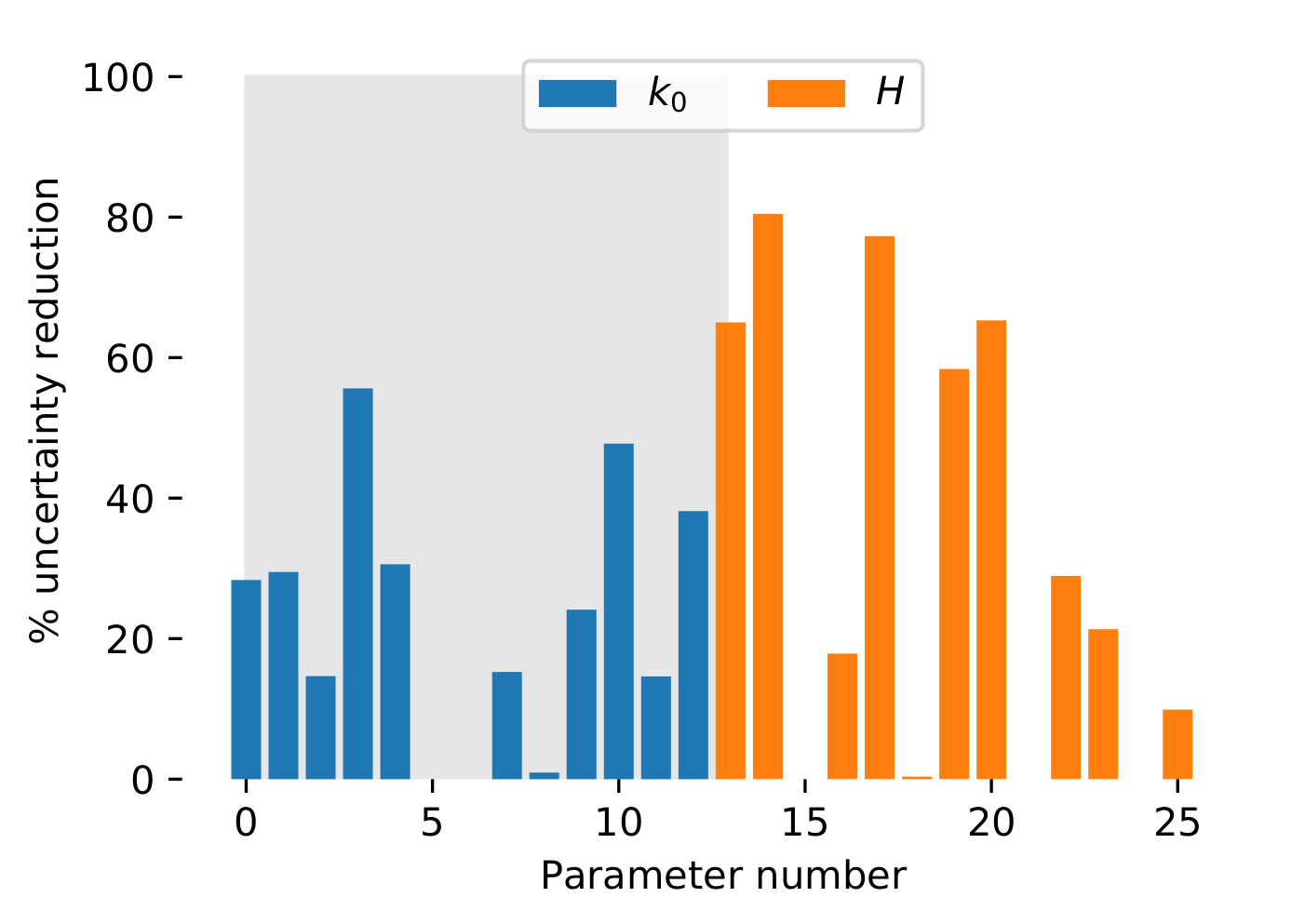
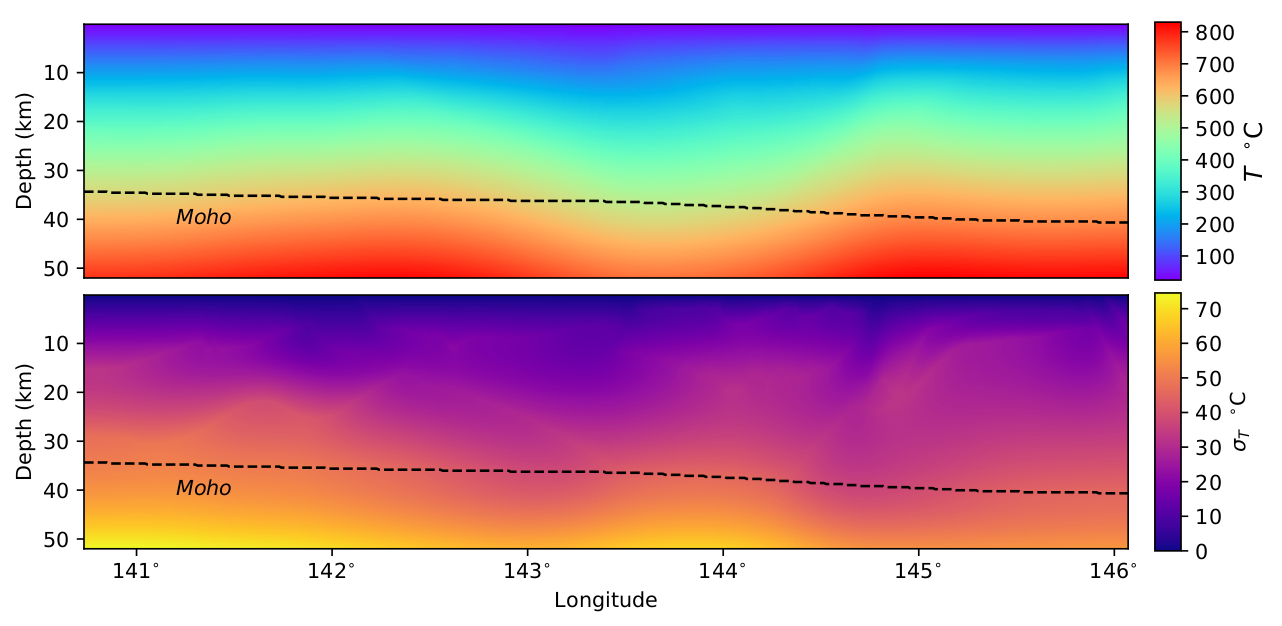
\delta\sigma = 1 - \frac{\sigma_{\mathrm{posterior}}}{\sigma_{\mathrm{prior}}}
δσ=1−σposteriorσprior\delta\sigma = 1 - \frac{\sigma_{\mathrm{posterior}}}{\sigma_{\mathrm{prior}}}

Uncertainty reduction

MAP estimate

Standard deviation

thermal

conductivity

heat production

Thermal model of Ireland

  • Significant heat refraction in Northern Ireland.
  • High temperature related to lateral branch of Iceland plume(?)

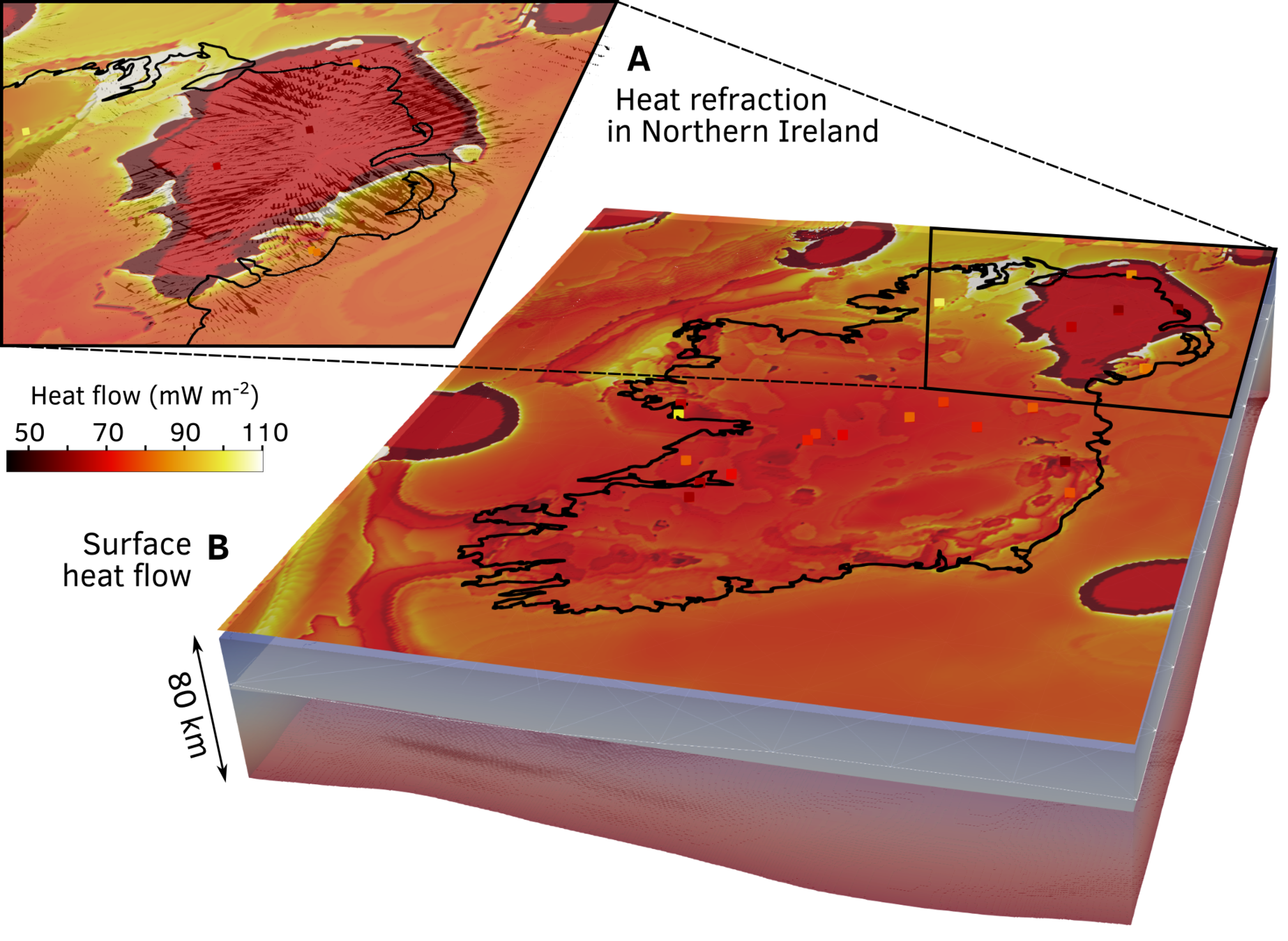
Temperature model with surface heat flow

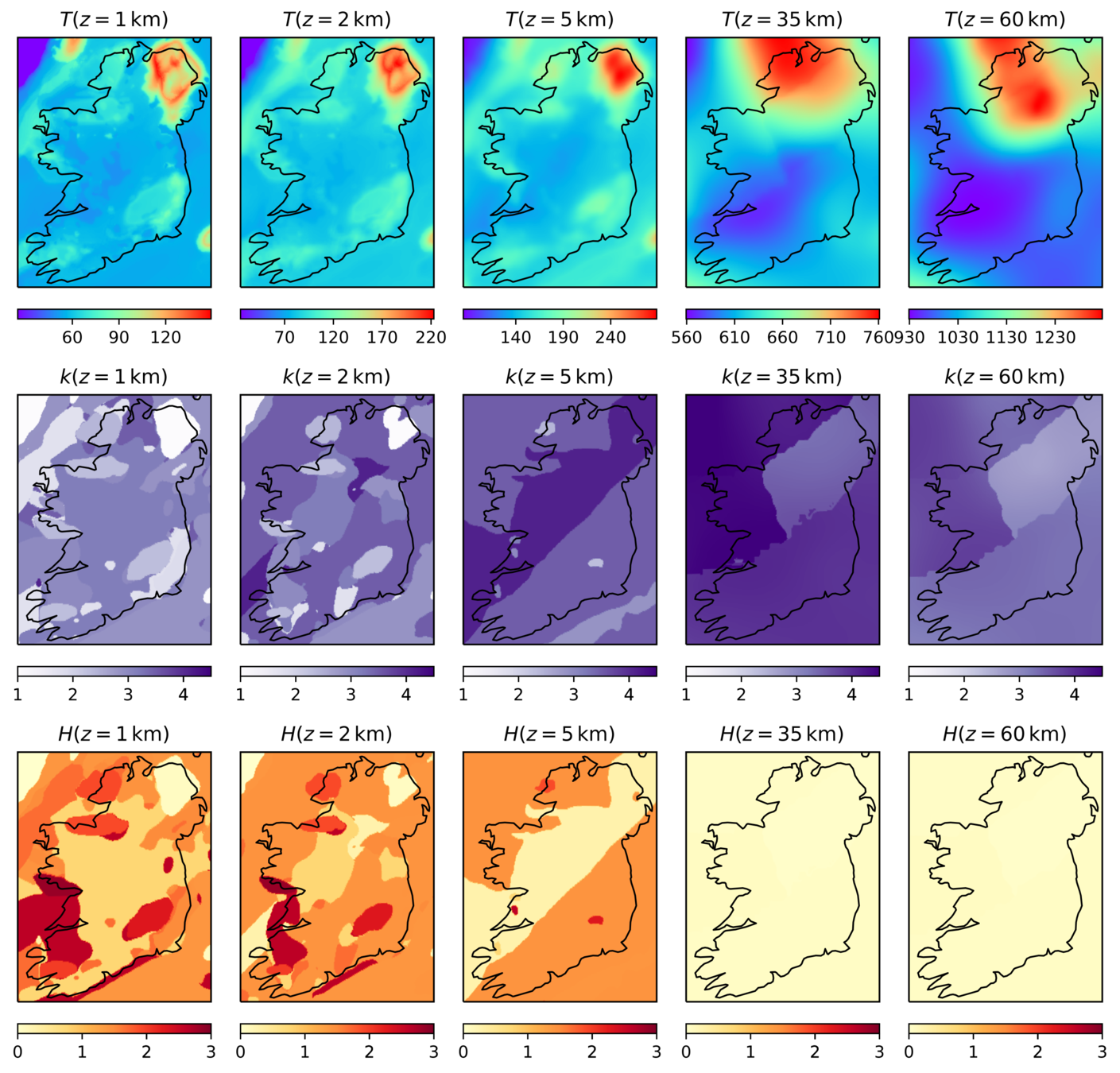
Temperature, thermal conductivity, heat production

at various depths

Thank you

Dr. Ben Mather

Madsen Building, School of Geosciences,

The University of Sydney, NSW 2006

https://benmather.info