Benedikt Eggemeier & Bodo Schwabe
(University of Göttingen)
Simulations of Axion Stars and Miniclusters
Axion Miniclusters
- Formation and mass growth
- Equilibration in halo and the core-halo mass relation
- Merger history
Axion Stars
- Minicluster-Halo Mass Function
- Minicluster morphology
- CDM velocity dispersion vs. granular structure in miniclusters
Axion Minicluster Halos


A. Vaquero, J. Redondo, and J. Stadler, JCAP, April 2019
Initial conditions
evolved with Gadget3-code
BE, J. Redondo, K. Dolag, J.C. Niemeyer, A. Vaquero, arXiv: 1911.09417
Minicluster Halo Mass Function


BE, J. Redondo, K. Dolag, J.C. Niemeyer, and A. Vaquero, arXiv: 1911.09417
before
after
matter-radiation equality
MCH Numbers and Morphology


- bound fraction at ?
- convergence of density profiles to NFW with decreasing redshift?
- differences in morphology between MCHs and "canonical" MCs?
BE, J. Redondo, K. Dolag, J.C. Niemeyer, and A. Vaquero, arXiv: 1911.09417
Future Work
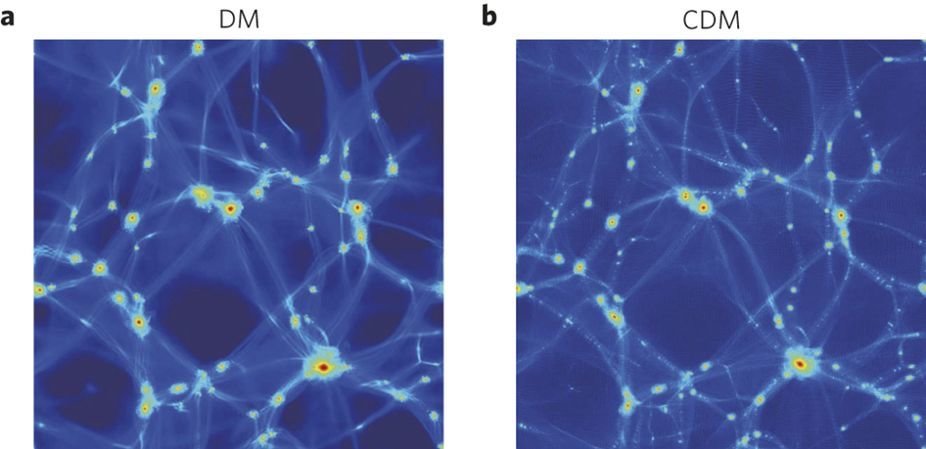
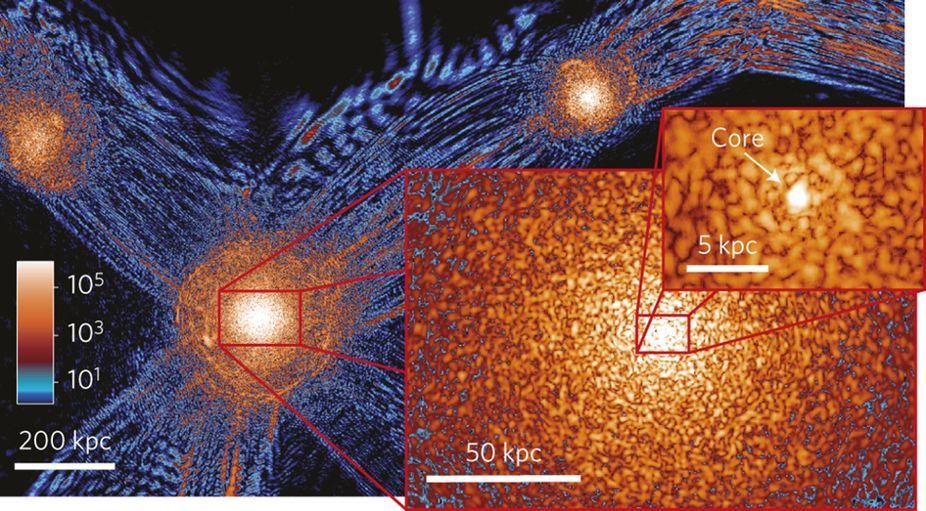
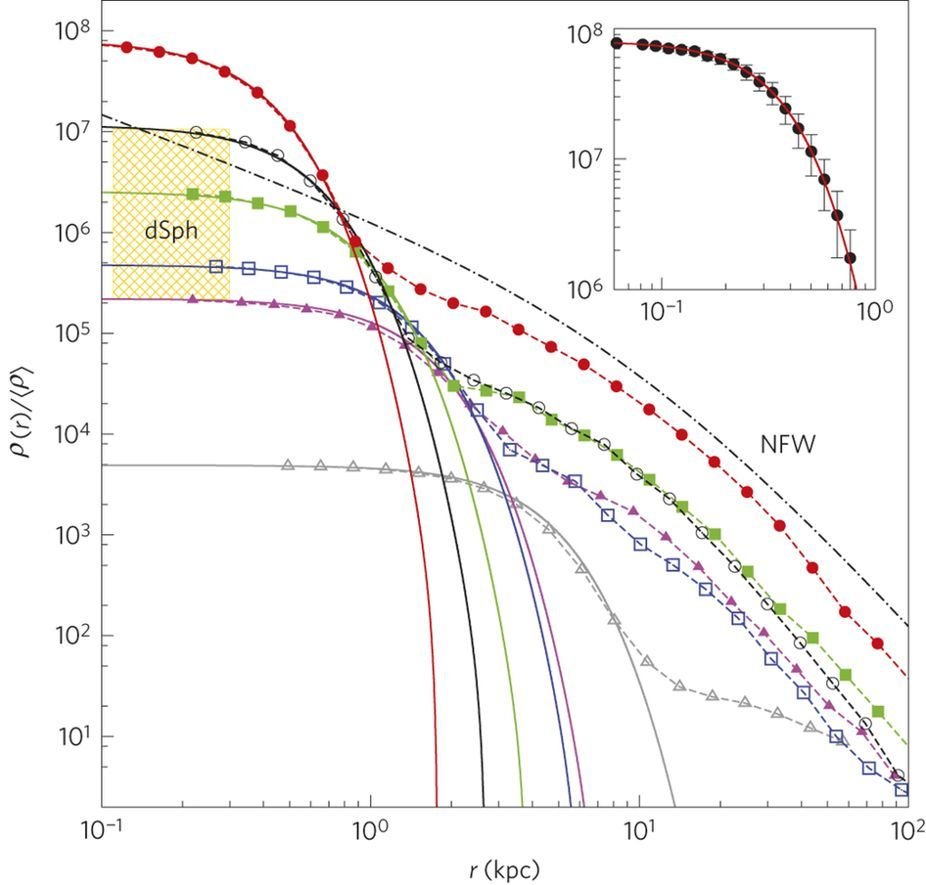
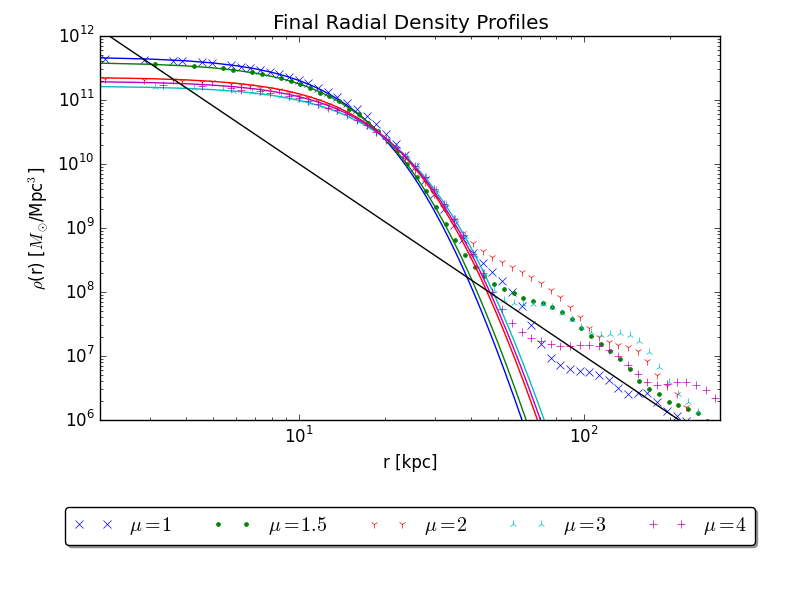
FDM Structure Formation
H.-Y. Schive, T. Chiueh, and T. Broadhurst, Nature Physics, 2014
Hybrid Method
Goal:
- AMR simulation
- Particle method on low resolution levels
- Finite-difference method on finest level
- Important: Boundary conditions between methods
Madelung transformation:
Initial phase:
Phase evolution:
Construction of wavefunction:
Note: Classical density -> no gradient energy and interference effects
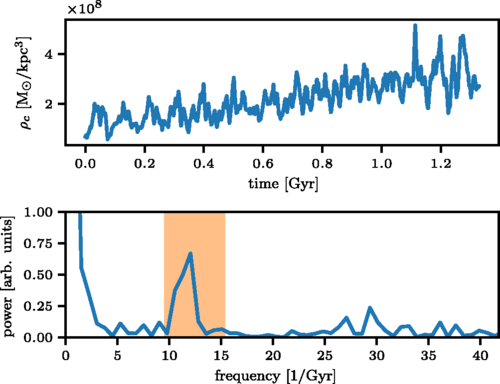
J. Veltmaat, J. C. Niemeyer, and BS, Physical Review D, August 2018.
Structure of FDM halos
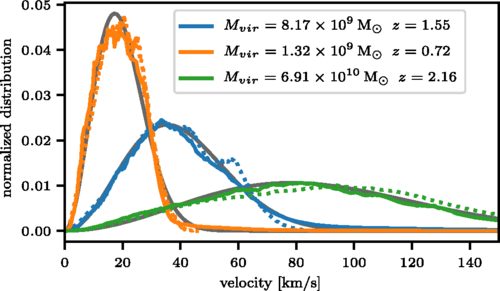
Velocity distribution:
Maxwellian distribution:

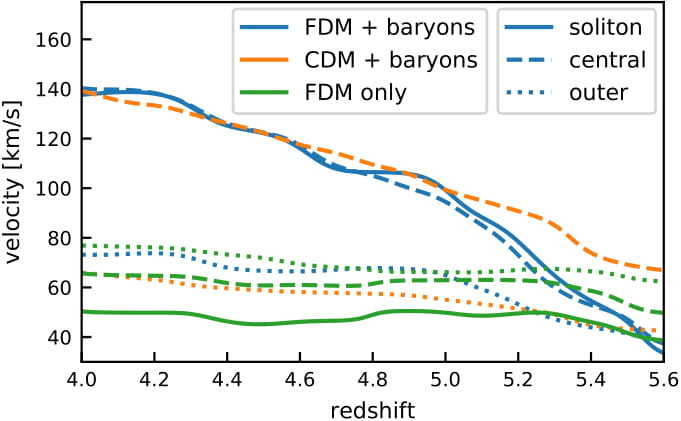
FDM dwarf galaxy with baryons
J. Veltmaat, J. C. Niemeyer, and BS, arXiv:1911.09614, November 2019.
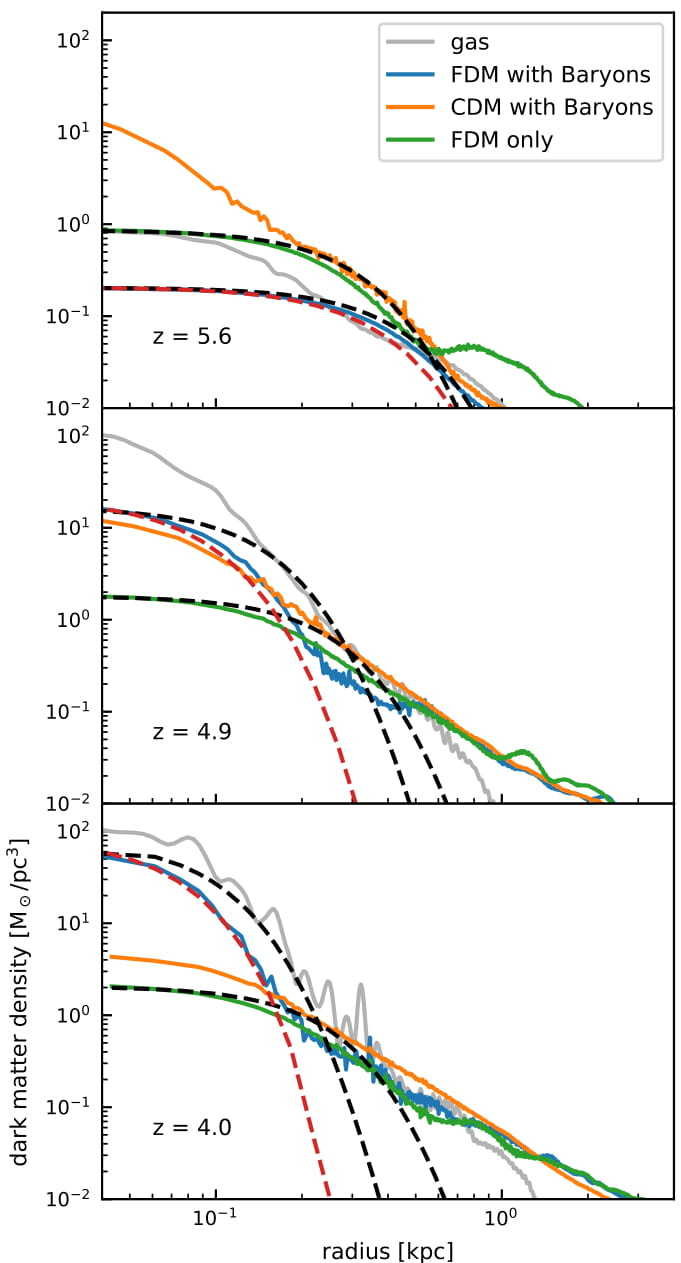
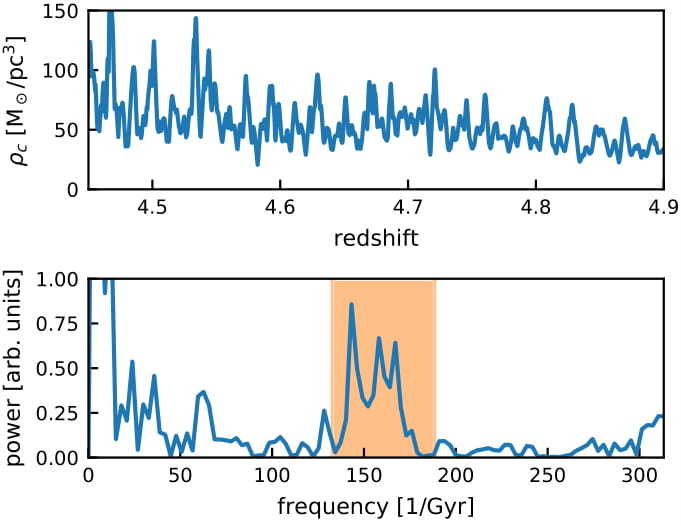
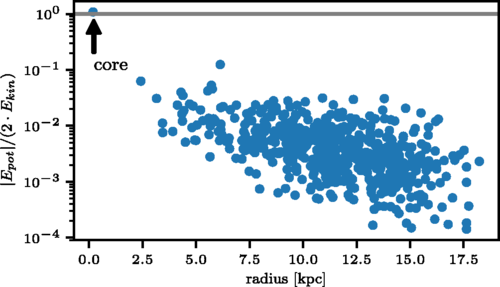
Axion Stars in Axion Miniclusters
Initial conditions


- take subvolumes of initial conditions
- evolve axion density field with SP equations
BE, and J.C. Niemeyer, Phys. Rev. D, September 2019
overall structure similar to DM halos and their central cores in FDM simulations
A. Vaquero, J. Redondo, and J. Stadler, JCAP, April 2019
BE, and J.C. Niemeyer, Phys. Rev. D, September 2019
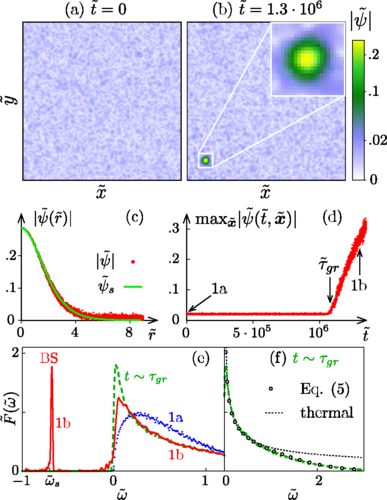
D.G. Levkov, A.G. Panin, I.I. Tkachev, Phys. Rev. Lett., October 2018
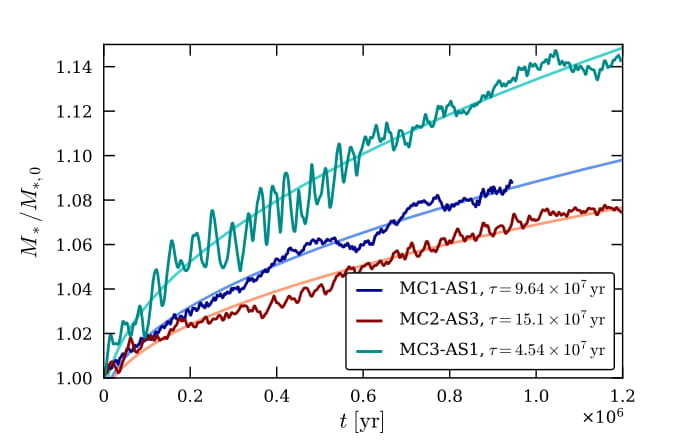
Mass Growth of Axion Stars in Axion Miniclusters

Axion Star Mergers
with
BE, and J.C. Niemeyer, Phys. Rev. D, September 2019
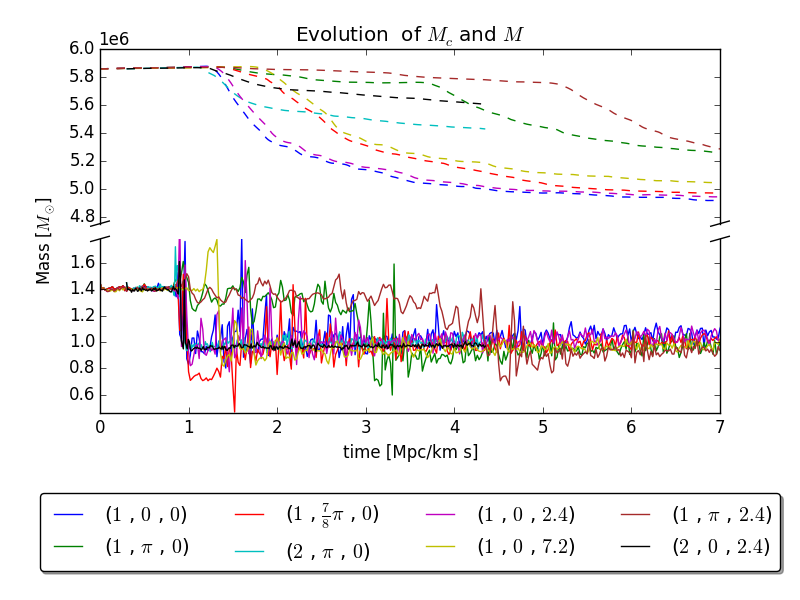
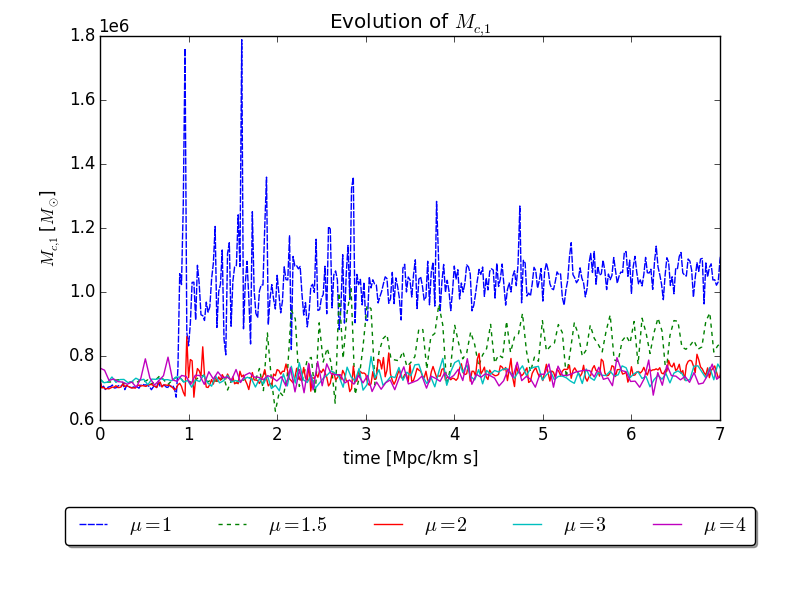
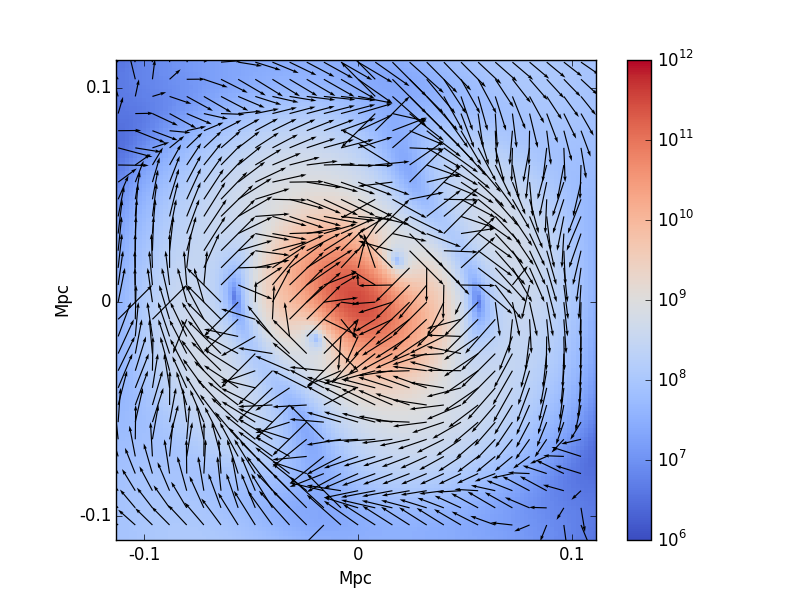
BS, J. C. Niemeyer, and J. F. Engels, Physical Review D, August 2016.
Binary Merger of Axion Stars
Recipe for Axion Star Evolution
- Bound axion star mergers result in new axion star
- Axion stars merge rapidly once they overlap
- Merger history is a series of binary mergers
- Only major mergers with mass ratio yield increased core mass
- Minor mergers and smooth accretion leave heavier axion star unchanged
- Numerically find
- Recover the scaling relation found in cosmological simulations
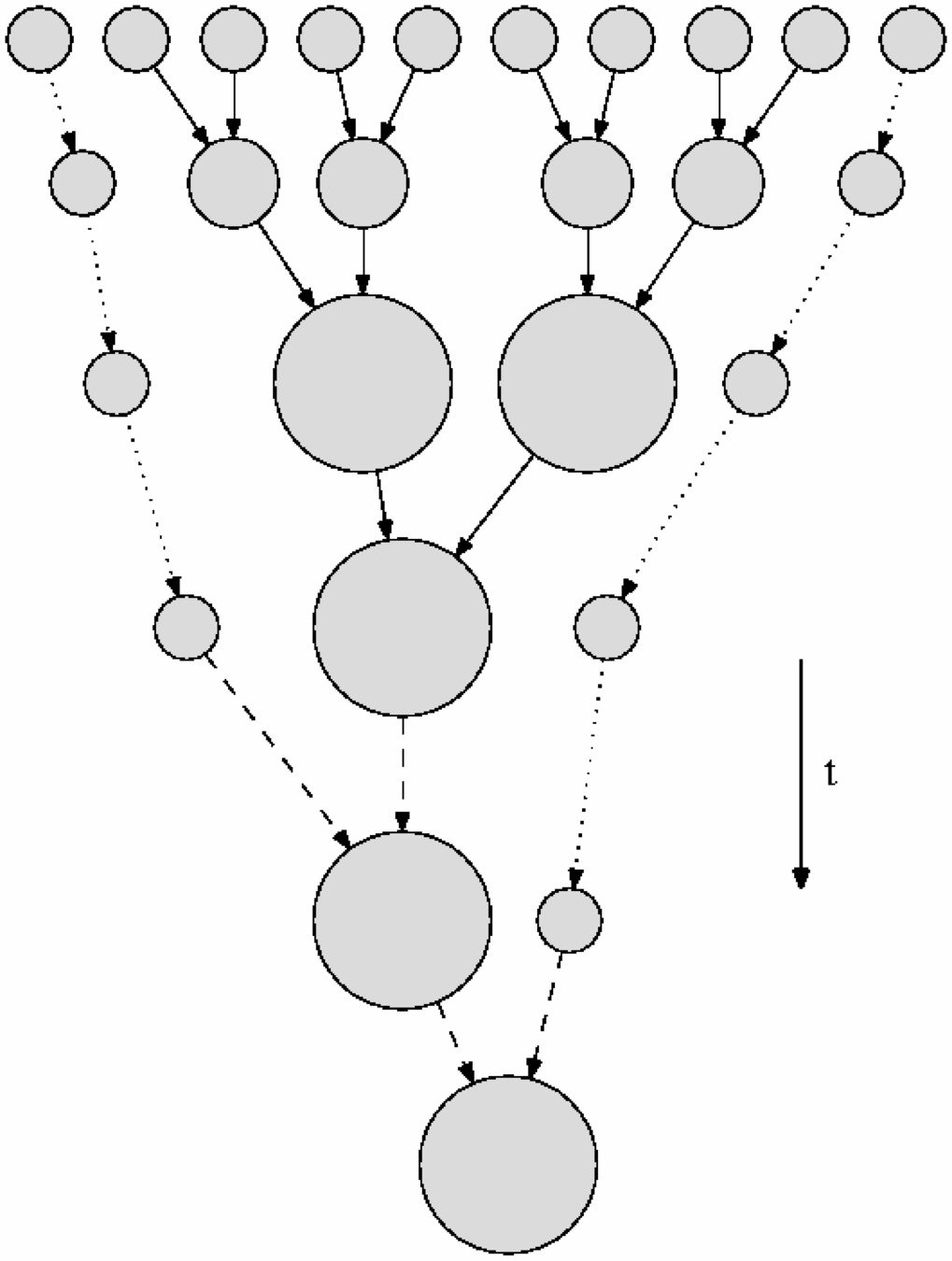
BS, J. C. Niemeyer, and J. F. Engels, Physical Review D, August 2016.
X. Du, C. Behrens, J. C. Niemeyer, and BS, Physical Review D, February 2017.
Summary and Conclusions
- Quantified abundance and morphology of axion miniclusters
- Investigated evolution of axion stars in minicluster halos
Local dark matter density is not yet well constrained but important for haloscope experiments
-- Need further dedicated axion structure formation simulations --


Backup: Power Spectrum

Backup: Minicluster Data

