Fuzzy Dark Matter on Galactic Scales
Bodo Schwabe
(University of Göttingen)
credit: J.Veltmaat
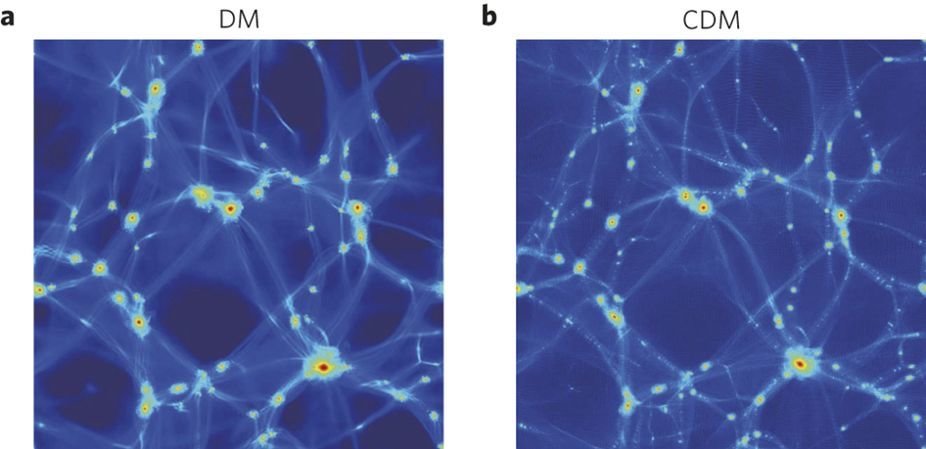
i\hbar\frac{\partial\psi}{\partial t} = -\frac{\hbar^{2}}{2ma^{2}}\nabla^{2}\psi+mV\psi
\nabla^{2}V = \frac{4\pi G}{a}\delta\rho
\delta\rho=|\psi|^{2}
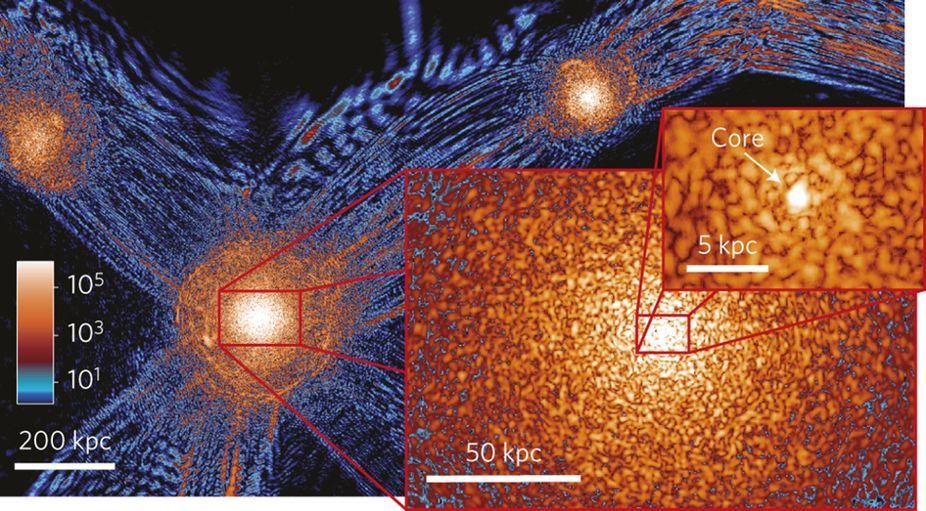
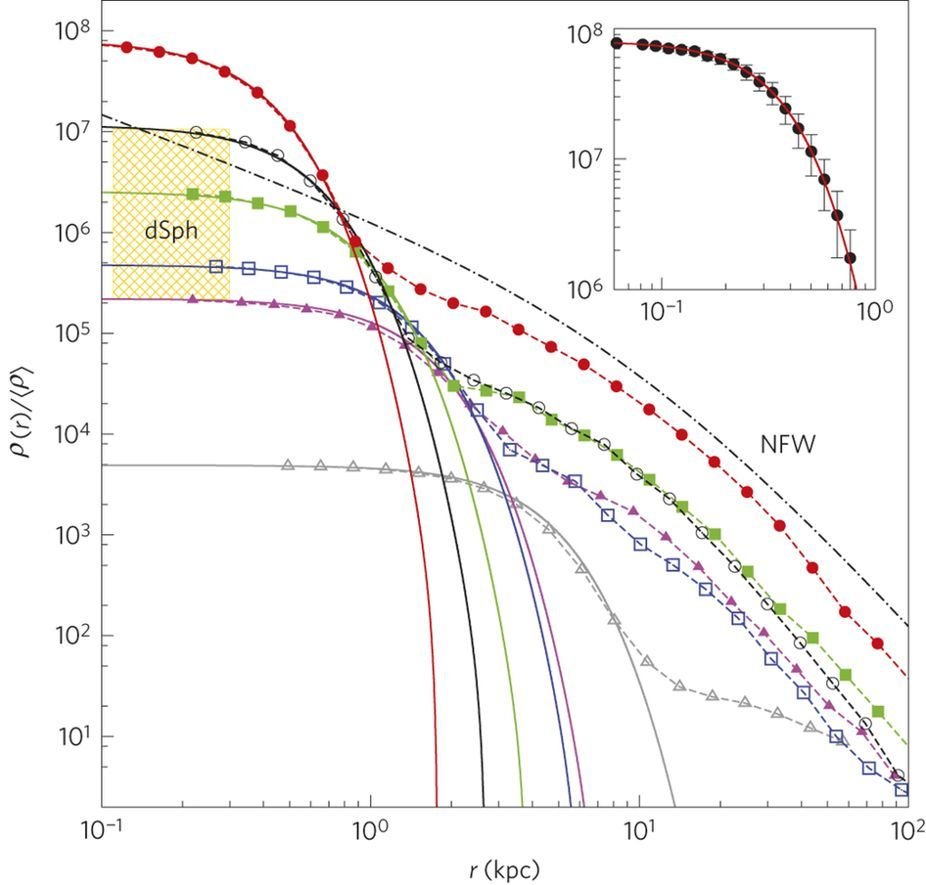
FDM Structure Formation
H.-Y. Schive, T. Chiueh, and T. Broadhurst, Nature Physics, 2014
\lambda_{\rm dB}\sim \hbar/mv_{\rm vir}\sim(\hbar/m)(G\rho)^{-1/2}r^{-1}
\tau_{\rm dB}\sim \hbar/mv^{2}_{\rm vir}
in three different scenarios
- Pure FDM
- FDM + Baryons
- FDM + CDM
Quantifying FDM Halo Dynamics
- Radial density profiles
- CDM velocity dispersion vs. FDM granular structure
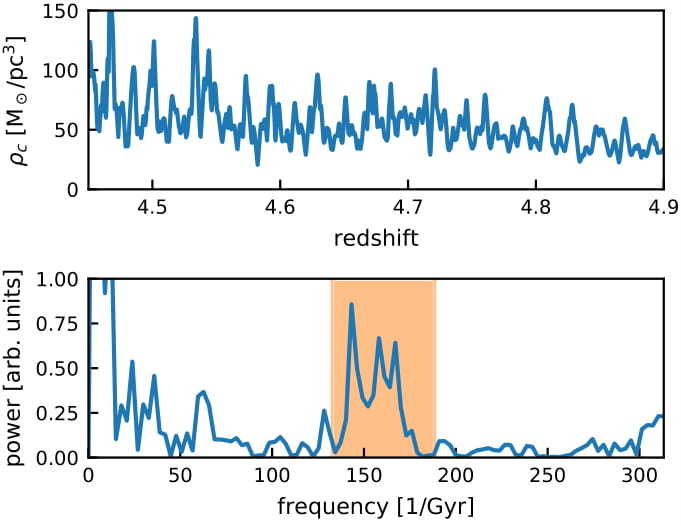
- Solitonic core dynamics
using
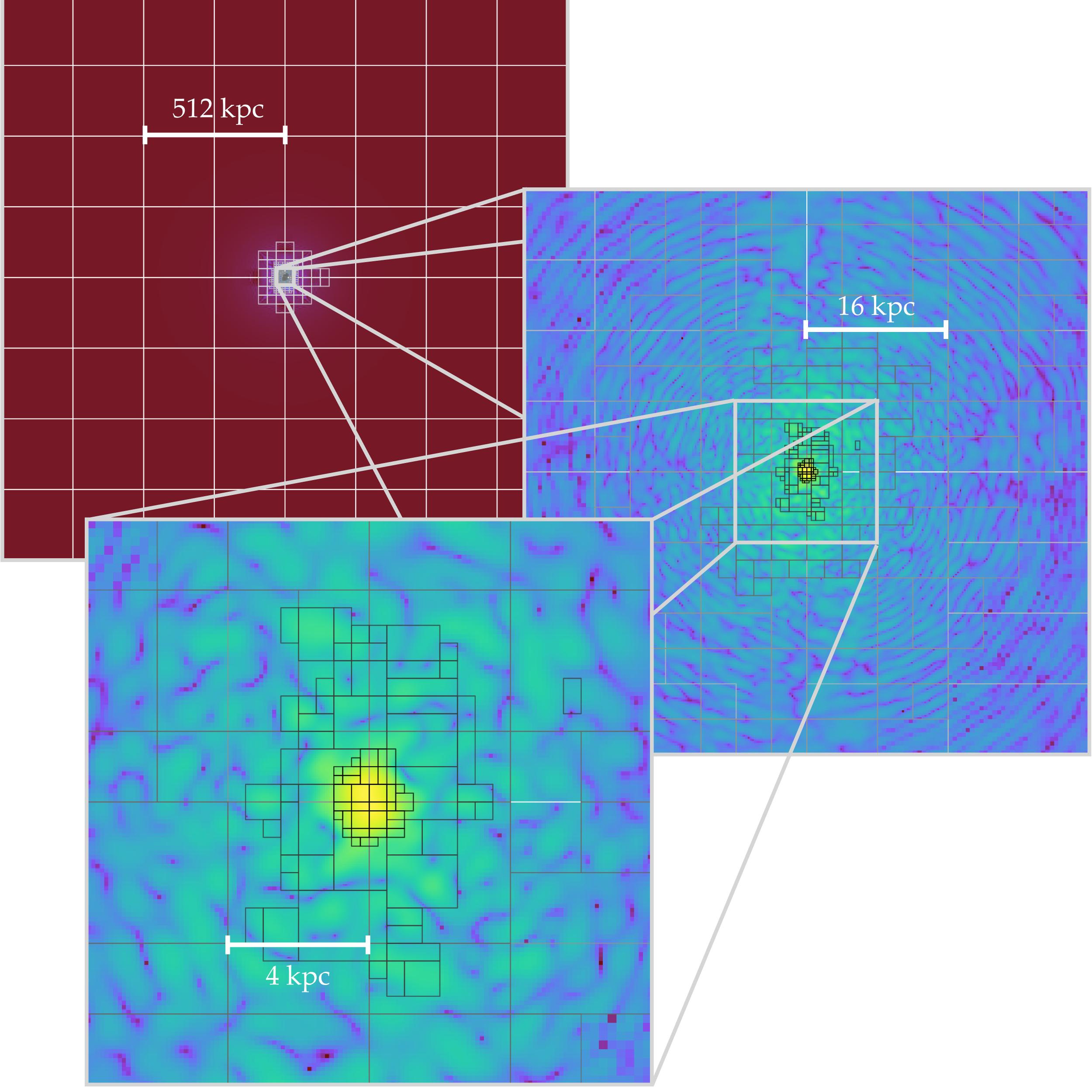
- AMR grid structures
- Hybrid particle+grid Methods
- Finite differencing
- Spectral codes
- N-body algorithms
Hybrid Method
Goal:
- AMR simulation
- Particle method on low resolution levels
- Finite-difference method on finest level
- Important: Boundary conditions between methods
Madelung transformation:
Initial phase:
Phase evolution:
Construction of wavefunction:
\Psi = A\exp[-iSm/\hbar]
\nabla\cdot v_{0} = a^{-1}\nabla^{2} S_{0}
\frac{\text d S_{i}}{\text d t} = \frac{1}{2} {v_i}^2 - V({x_i})
A({x}) = \sqrt{\sum_i W({x} - {x_i})}
\qquad S({x}) = \frac{\hbar}{m}\arg\left[\sum_i \sqrt{W({x} - {x_i})} e^{i(S_i + {v_i}\cdot a({x}-{x_i}))m/\hbar}\right]
Note: Classical density -> no gradient energy and interference effects
Goal:
- AMR simulation
- Particle method on low resolution levels
- Finite-difference method on finest level
- Important: Boundary conditions between methods
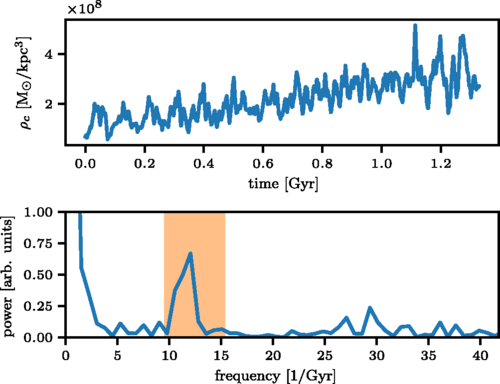
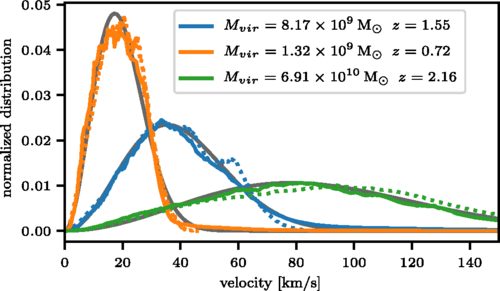
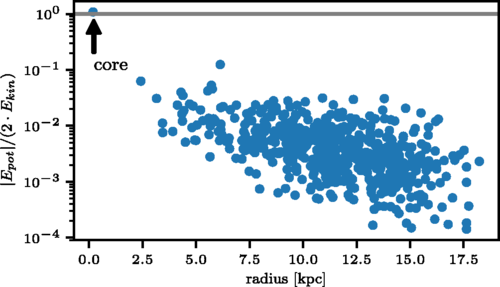
J. Veltmaat, J. C. Niemeyer, and BS, Physical Review D, August 2018.
Structure of FDM Halos
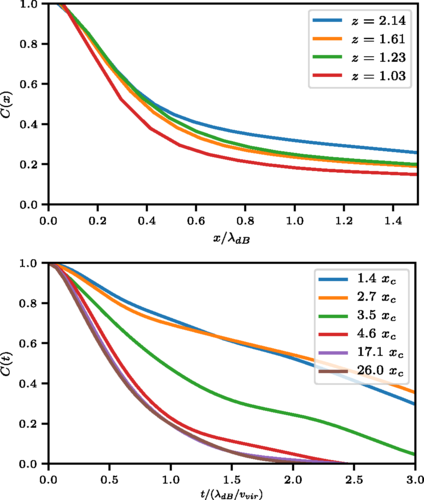

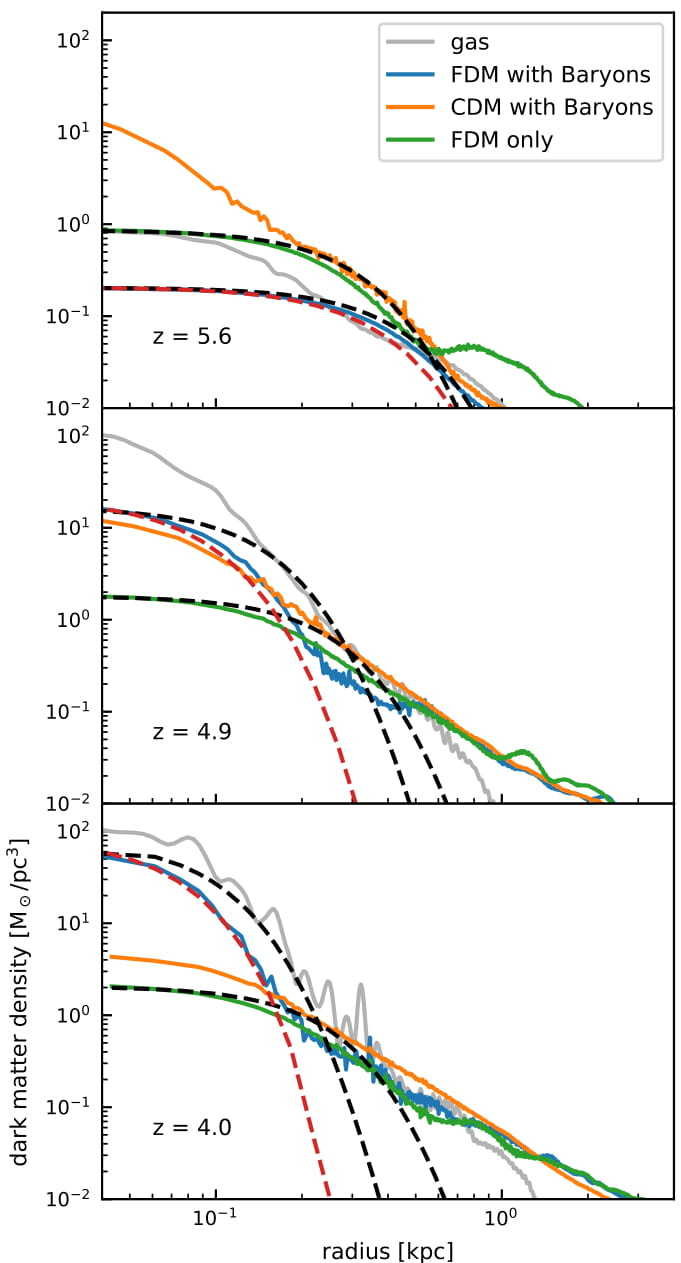
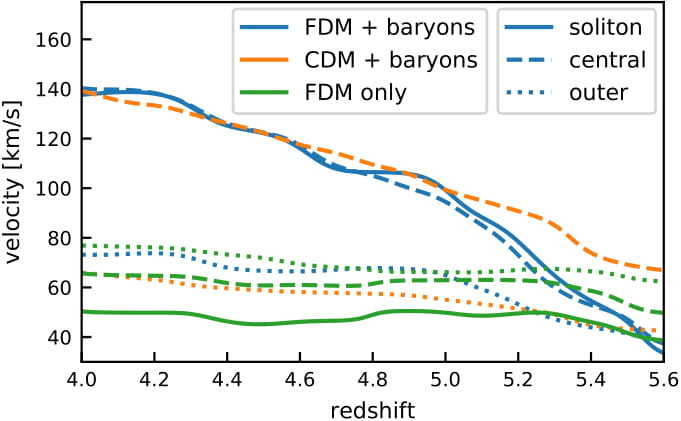
FDM Dwarf Galaxy with Baryons
J. Veltmaat, BS, and J. C. Niemeyer, Physical Review D, April 2020.
AxioNyx: Simulating Mixed Fuzzy and Cold Dark Matter
Goal:
- AMR simulations for Mixed Dark Matter
- CDM -> N-body scheme
- FDM -> Spectral/Finite-difference method
- Baryonic physics -> Nyx modules for hydrodynamics and feedback
BS, Mateja Gosenca, Christoph Behrens, Jens C. Niemeyer, and Richard Easther, in prep.
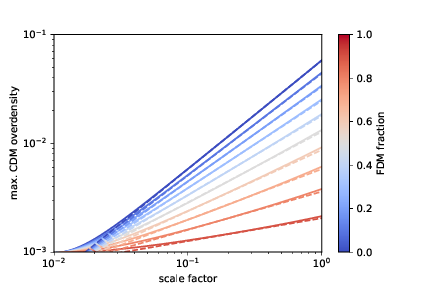
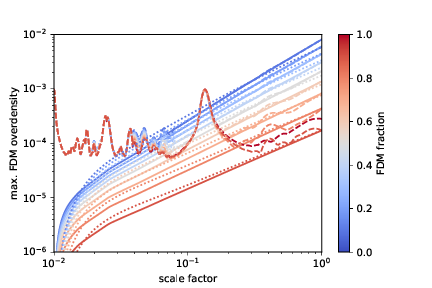
Spherical Collapse - linear
\ddot{\delta}_{\rm FDM}+2H\dot{\delta}_{\rm FDM}+\left(\frac{k^{4}\hbar^{2}}{4m^{2}a^{4}}-4\pi Gf\overline{\rho} \right)\delta_{\rm FDM} = 4\pi G(1-f)\overline{\rho}\delta_{\rm CDM}\\
\ddot{\delta}_{\rm CDM}+2H\dot{\delta}_{\rm CDM}-4\pi G(1-f)\overline{\rho}\delta_{\rm CDM} = 4\pi Gf\overline{\rho}\delta_{\rm FDM}
\delta_{\rm CDM}(a) \propto a^{(\sqrt{1+24(1-f)}-1)/4}
\delta_{\rm FDM}(a) \propto a^{(\sqrt{1+24(1-f)}+3)/4}
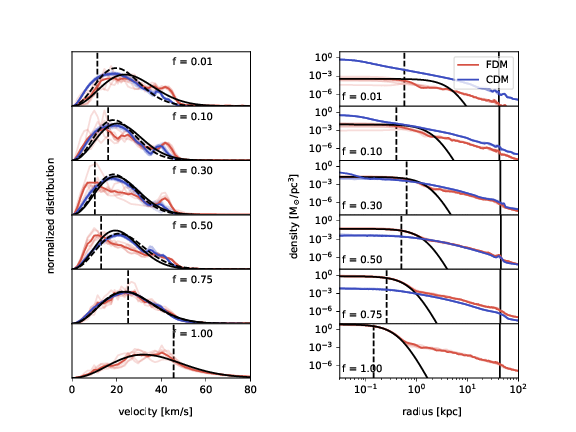
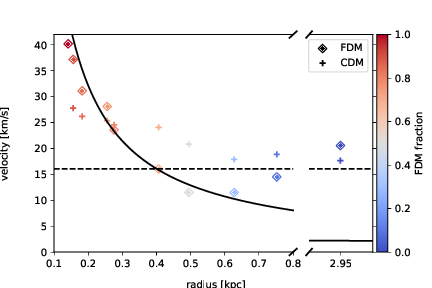
Spherical Collapse - Non-linear
v_c=\frac{2\pi}{7.5}\frac{\hbar}{mr_c}
f(\textbf{v}) = \frac{1}{N}\left|\int\text{d}^3 x\exp\left[-im\textbf{v}\cdot\textbf{x}/\hbar\right]\psi(\text{x})\right|^2
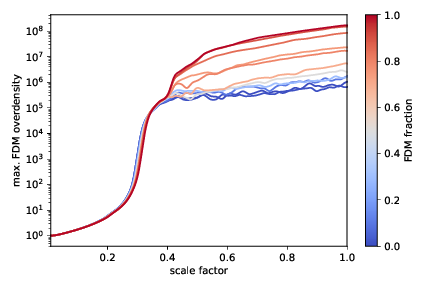
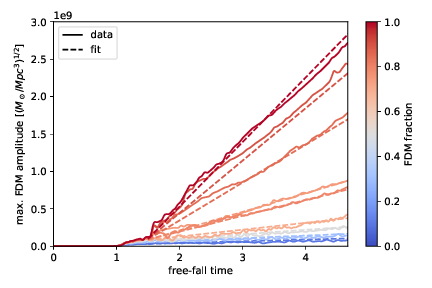
Spherical Collapse - Non-linear
A(t) = A_{1}\cdot (t-t_{0})/\tau_{\text{gr}}+A_{0}f^{1/2}
\tau_{\text{gr}} = \frac{0.7\sqrt{2}}{12\pi^3}\frac{m^3v_c^6}{G^2\rho_{c}^2\Lambda}\simeq 0.015 \frac{t_c}{\Lambda}
Conclusions
-
Distinguishing features of FDM: Strong stochastic density fluctuations in halos on deBroglie length and time scales and formation of stable, oscillating soliton cores in center of halos
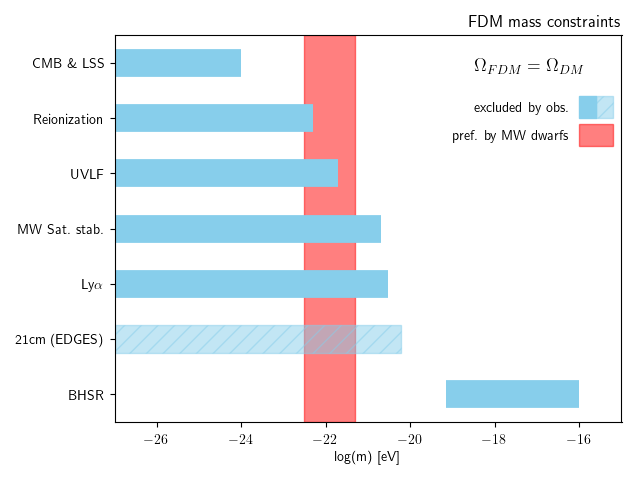
- Local FDM density important for experiments but not well constraint yet
- Heavier FDM mass can be best constrained on non-linear, galactic scales (soliton osc., soliton mergers, gravitational heating/cooling, tidal disruption,...)
-- Need further dedicated FDM simulations on galactic scales --
m<10^{-21}\,\text{eV}
- FDM structure formation similar to CDM on super deBroglie scales (except cut-off in initial power spectrum as for WDM)
- Weakly non-linear probes like Lyman-alpha exclude