AxioNyx: Simulating Mixed Fuzzy and Cold Dark Matter
Goal:
- AMR simulations for Mixed Dark Matter
- CDM -> N-body scheme
- FDM -> Spectral/Finite-difference method
- Baryonic physics -> Nyx modules for hydrodynamics and feedback
Bodo Schwabe, Mateja Gosenca, Christoph Behrens, Jens C. Niemeyer, and Richard Easther, Physical Review D, October 2020.
Spherical Collapse
v_c=\frac{2\pi}{7.5}\frac{\hbar}{mr_c}
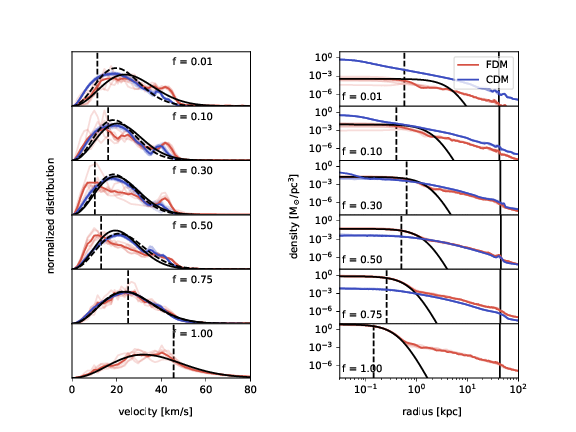
Schroedinger-Vlasov correspondence:
- Maxwellian FDM Powerspectrum of central region coincides well with particle velocity dispersion.
- Outer radial density profiles have constant FDM/CDM density ratio
For f>0.1 a soliton forms with velocity close to maximum in spectrum indicated by dashed line
Spherical Collapse
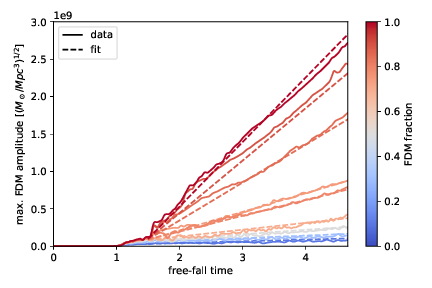
Soliton amplitude grows linearly in time. Rate determined by FDM/CDM ratio
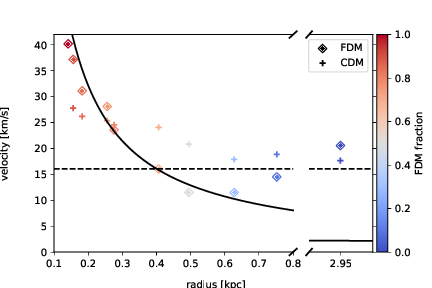
Peaks of velocity spectra:
- Exceed virial velocity (horizontal line) for large FDM ratios.
- Close to core velocities (solid line)
- Core masses in isolated halos exceed core-halo mass relation
New Hybrid Method
Goal:
- AMR simulation
- Particle method on low resolution levels
- Finite-difference method on finest level
- Important: Boundary conditions between methods
Madelung transformation:
Initial phase:
Phase evolution:
Construction of wavefunction:
Gauss kernel:
\Psi = A\exp[-iSm/\hbar]
\nabla\cdot v_{0} = a^{-1}\nabla^{2} S_{0}
\frac{\text d S_{i}}{\text d t} = \frac{1}{2} {v_i}^2 - V({x_i})
\qquad \Psi({x}) = \sum_i W({x} - {x_i}) A_i e^{i(S_i + {v_i}\cdot a({x}-{x_i}))m/\hbar}
Goal:
- AMR simulation
- Particle method on low resolution levels
- Finite-difference method on finest level
- Important: Boundary conditions between methods
W(x-x_i) = \frac{\gamma^{3/2}\Delta^{3}x}{\pi^{3/2}}\exp\text{[}-\gamma(x-x_i)^{2}\text{]}\theta(x-x_i)
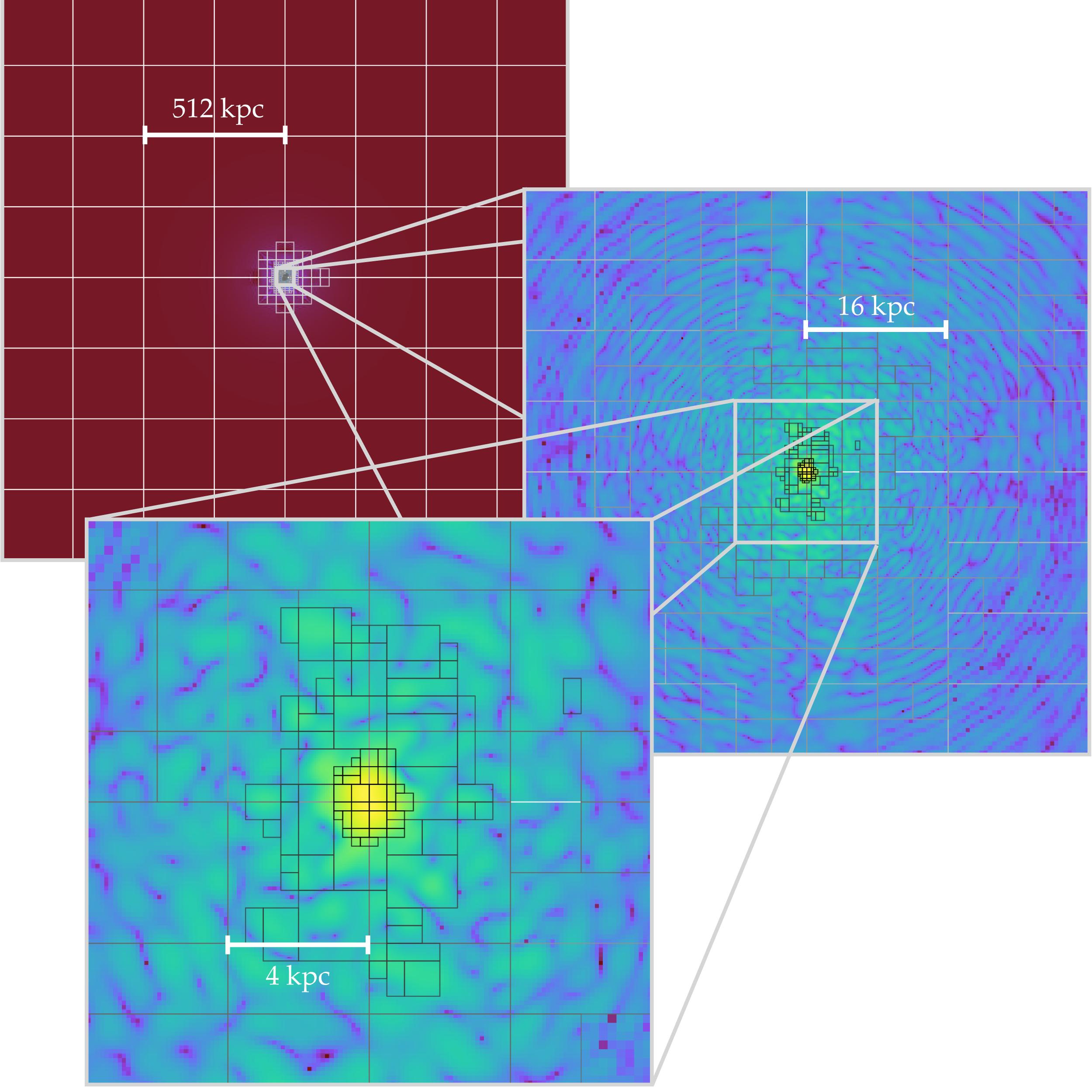
Agora Simulation
DM-only comparison run (60 Mpc/h) between various codes:
zoom-in simulation focusing on isolated halo


Axionyx N-body run with CDM initial conditions
Axionyx N-body run with FDM initial conditions
Gauss Beam Reconstruction

- Restart FDM N-body simulation at z=3:
- Reconstruct wavefunction at amr level 11 in the inner most halo region (virial radius at 50kpc)
- Add 3 finite difference levels
The granular structure and central soliton is clearly visible
Agora Simulation


- FDM Powerspectrum and underlying particle velocity dispersion correspond well to each other.
- Halo velocities have not yet relaxed into Maxwell spectrum (but do so later on)
- Soliton velocity (grey line) at peak in spectrum
- FDM radial density profile with soliton core and NFW outer tail