Problem Statement​

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?

Model it as a Graph

What's a GRAPH?

representation of a set of objects where some pairs of objects are connected by links

EdgeS

Ordered or Unordered pair of exactly 2 vertices.

Vertices

Fundamental unit of a graph. Think of it as a point. Can be disconnected.

GRAPH

Ordered Pair G =(V, E)
V = Set of vertices
E = Set of edges

Directed

Edges are two way

 

Edge(a,b) != Edge(b,a)

Undirected

Edges have no orientation. 

 

Edge(a,b) =  Edge(b,a)

 

Asymmetric

In the asymmetric TSP, paths may not exist in both directions or the distances might be different, forming a directed graph.

One-way streets, for eg.

symmetric

The distance between two cities is the same in each opposite direction, forming an undirected graph.

This symmetry halves the number of possible solutions.

 

Most common type of TSP.

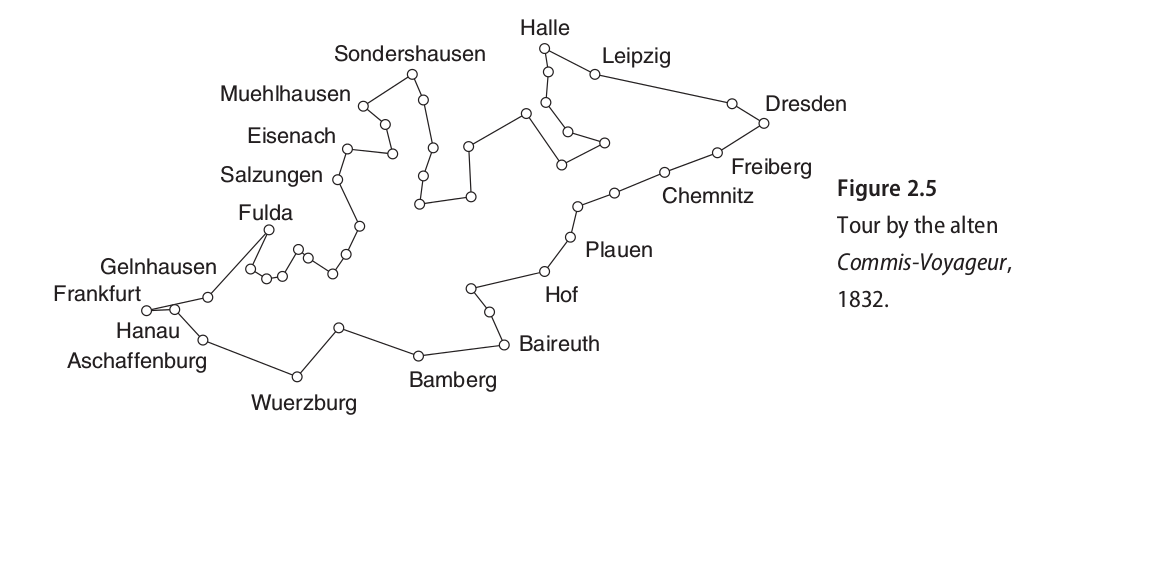
Problem Statement

undirected weighted graph

city = graph's vertices

path = graph's edges

distance = edge's length

Minimize total distance after visiting all vertices.

 

Often, graph is complete as well

Solve*
TSP
=
GET
$1,000,000

Problem Complexity

ComplexiTY

Year	Vertices
1954	49 Cities (USA)
1971	64 Points
1975	80 Points
1977	120 Cities (Germany)
1987	318 Points
1987	532, 666, 1002, 2392
1992	3038 Points

TSP Records

1998 - 13,509 Cities
in USA

SWEDEN (2004)

 

24978 Cities

85,900
Points

Computer Chip Production

(2006)

Applications

Navigation

Mapping GEnomes

Printed Circuit Boards

Other Fields

• Data Mining
• Slewing
• X-ray Crystallography
• Engravings, Etchings
• Custom Chip Mfg.
• Cutting patterns
• Compression

Solutions

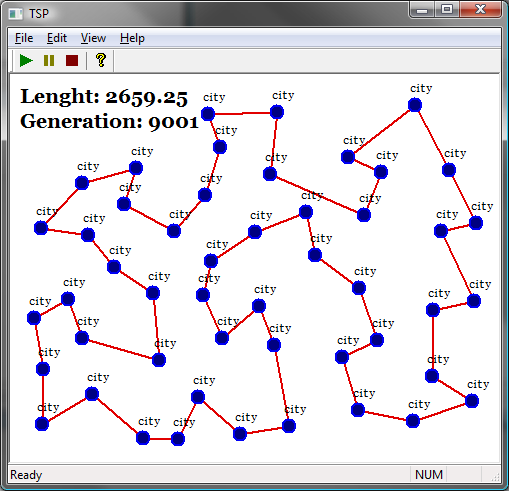
Brute Force Search

Nearest Neighbour

Greedy Algorithm

Partial Tour
Method

Ant Colony Optimization

1. Travel to all cities
2. Choose closer cities (visibility)
3. Probability of choosing ∝ pheromone
4. Deposit pheromone on path travelled
5. Iterate

References

• By David Stanley from Nanaimo, Canada (Balloon Salesman  Uploaded by russavia) [CC-BY-2.0], via Wikimedia Commons
• TSP Cartoon, Courtesy Randal Munroe (xkcd.com)
• In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation, William J Cook

William J COOK

 

In Pursuit
of the
Travelling
Salesman