\dfrac{3-x-2^x}{\pi^x-\pi^4}>0 \iff h(x)=\dfrac{f(x)}{g(x)}>0
-
Procuramos os números inteiros que não satisfazem a inequação dada, i.e., procuramos as soluções inteiras da inequação
- \(f(x)\) é decrescente em \(\mathbb R\) e, como tal, tem, no máximo, um zero. Como \(f(1)~=~0\), à esquerda de 1 é positiva e negativa à sua direita;
- \(g(x)\) é uma função crescente em \(\mathbb R\) e, como tal, tem, no máximo, um zero. Como \(f(4) = 0\), à esquerda de \(4\) é negativa e à sua direita positiva. Assim, \(4 ~\notin~D_h\).
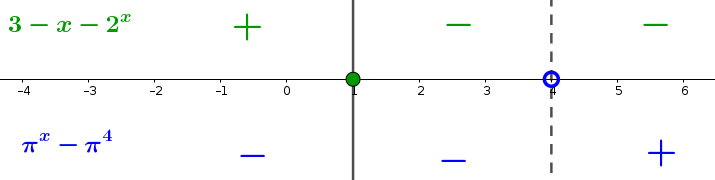
- Assim, \(\dfrac{3-x-2^x}{\pi^x-\pi^4}>0 \iff x\in]1,4[\);
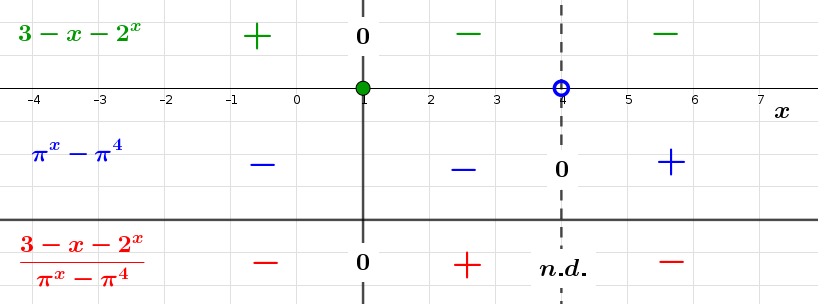
- Neste intervalo apenas \(2\) e \(3\) são inteiros. Logo, \(2+3=5\).