Smallest Enclosing Circle

22601 王政祺、22625 劉至軒

What do we need to solve ?

Router Problem

Imagine that you're a network provider....

You have to set up a hotspot for all of your users...

BUT!

The farther the hotspot reaches, the more expensive it gets

To limit our problem further, you may only use one router.

Define our problem:

Given a set of points on the plane. Is there any point that is within a certain distance of these points?

Where do we place a point that minimizes the maximum distance to a set of points?

Given a set of points on the plane, compute the smallest enclosing circle.

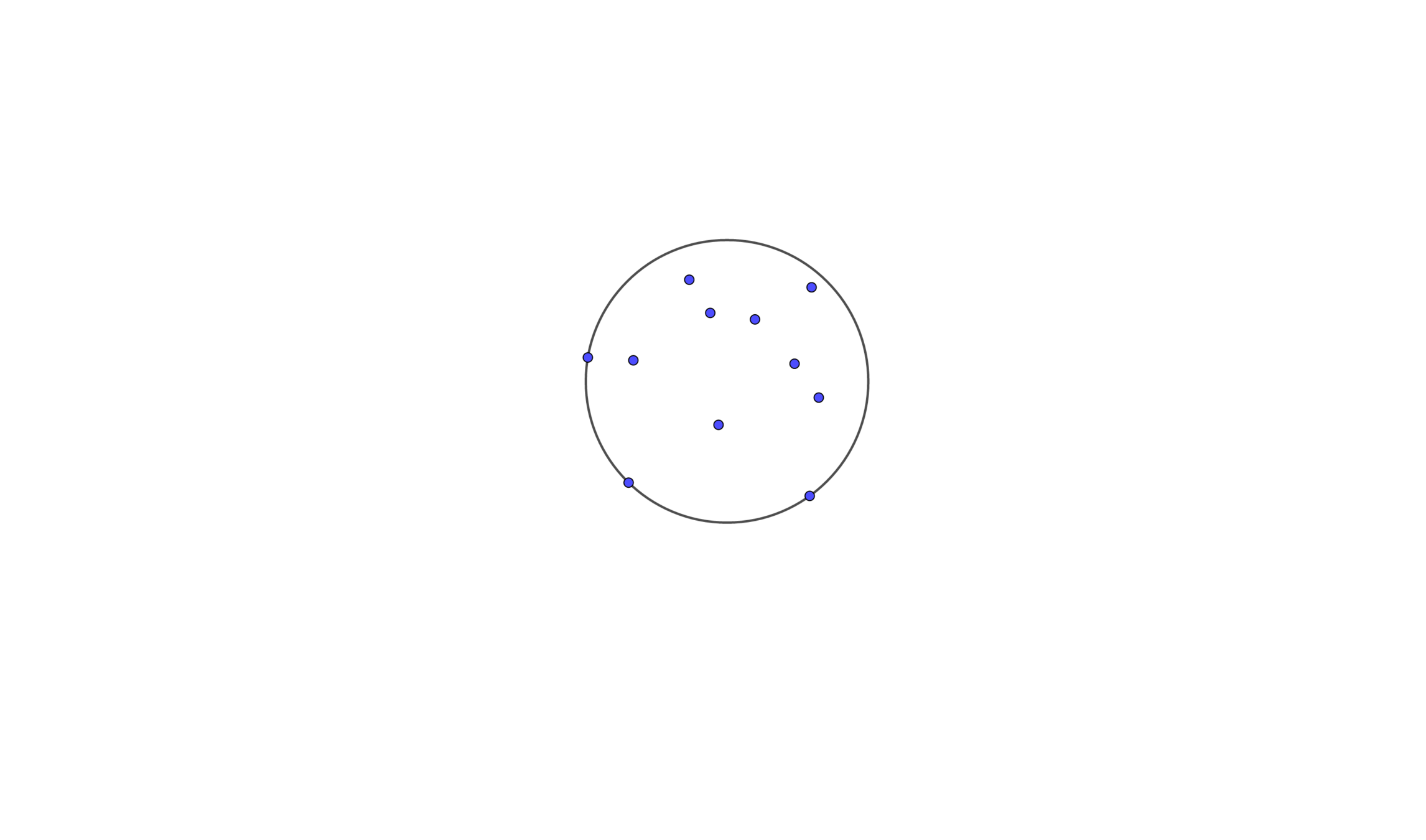
The enclosing circle must pass through some of those points, or else it won't be the smallest circle

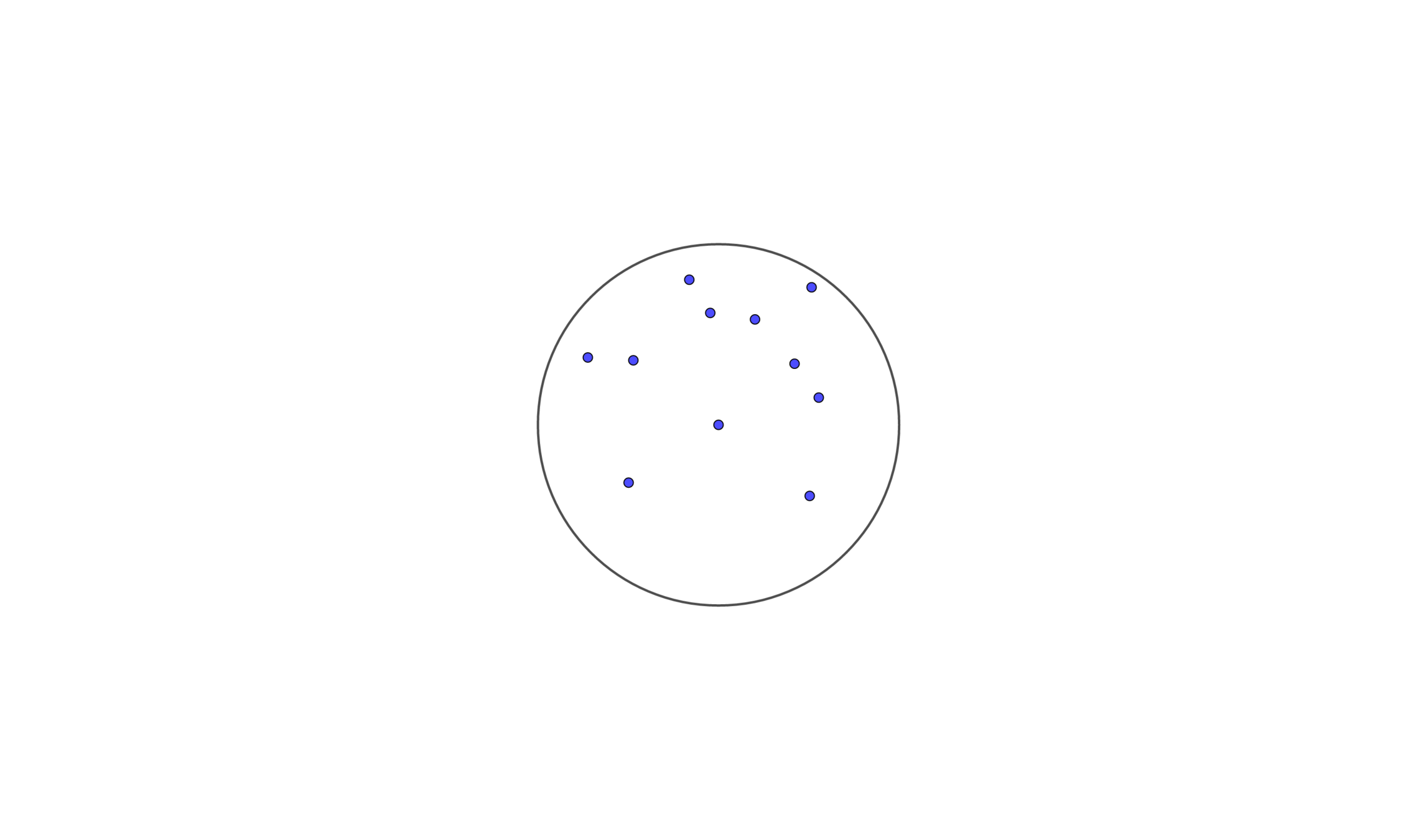
A smallest enclosing circle has (at least) three points on its boundary, or only two if they are diametrically opposite

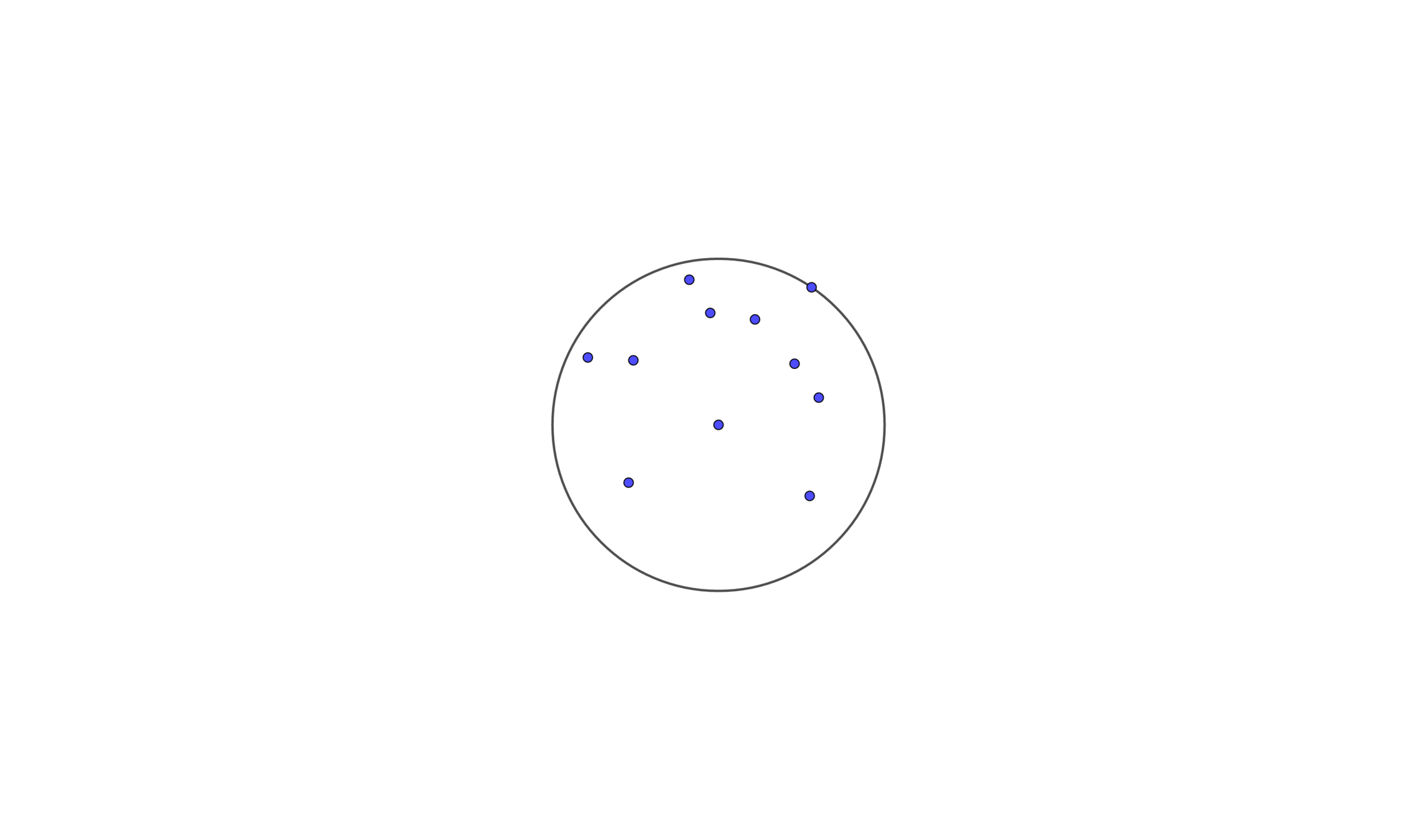
Randomized Incremental Construction

Let \(p_1, p_2 , \cdots , p_n\) be the points in random order

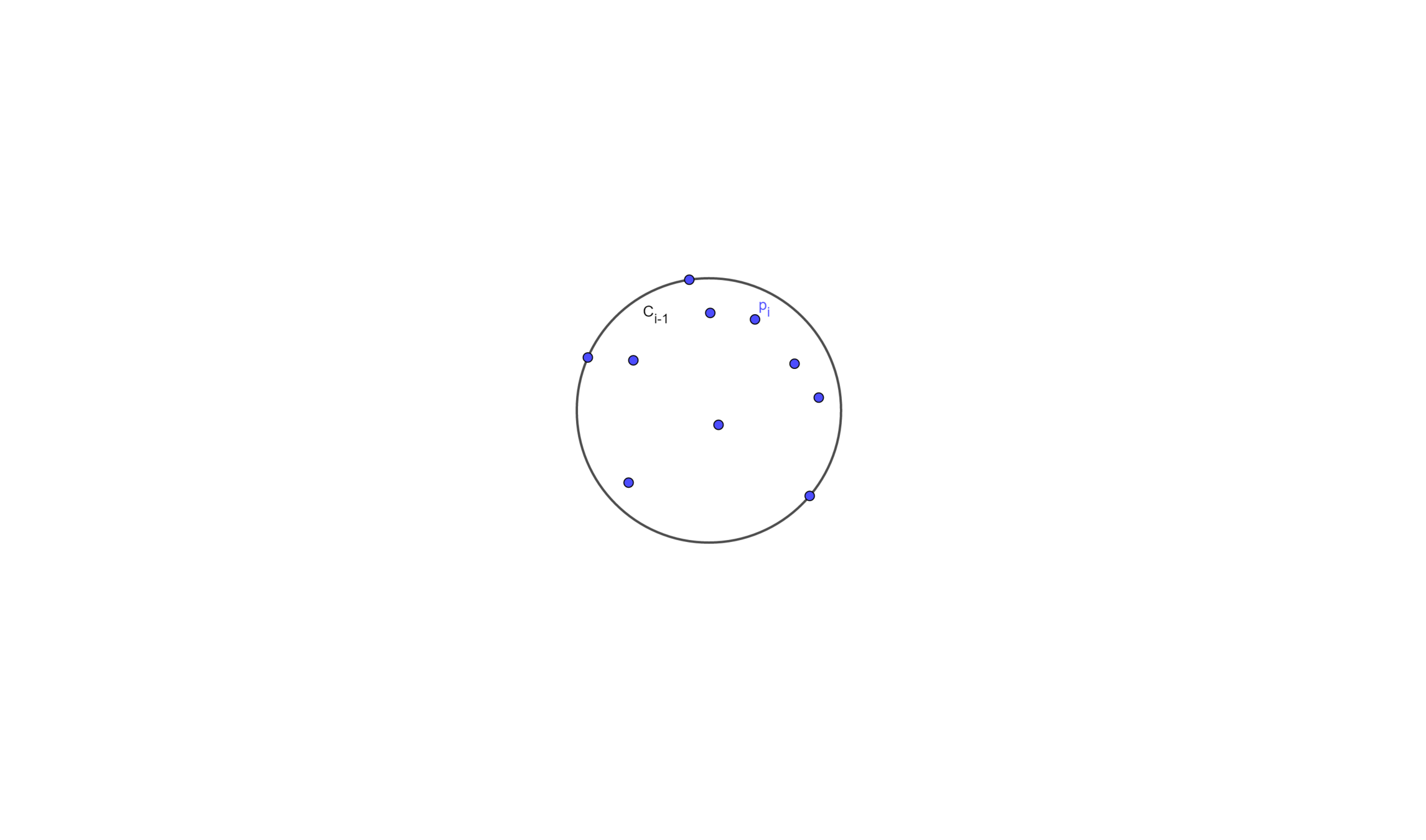
Let \(C_i\) be the smallest enclosing circle for \(p_1 , \cdots , p_i\)

Suppose we know \(C_{i-1}\), and we wants to add a point \(p_i\)

If \(p_i\) is inside \(C_{i-1}\), then \(C_i = C_{i-1}\)
Else then \(C_i\) will have \(p_i\) on its boundary

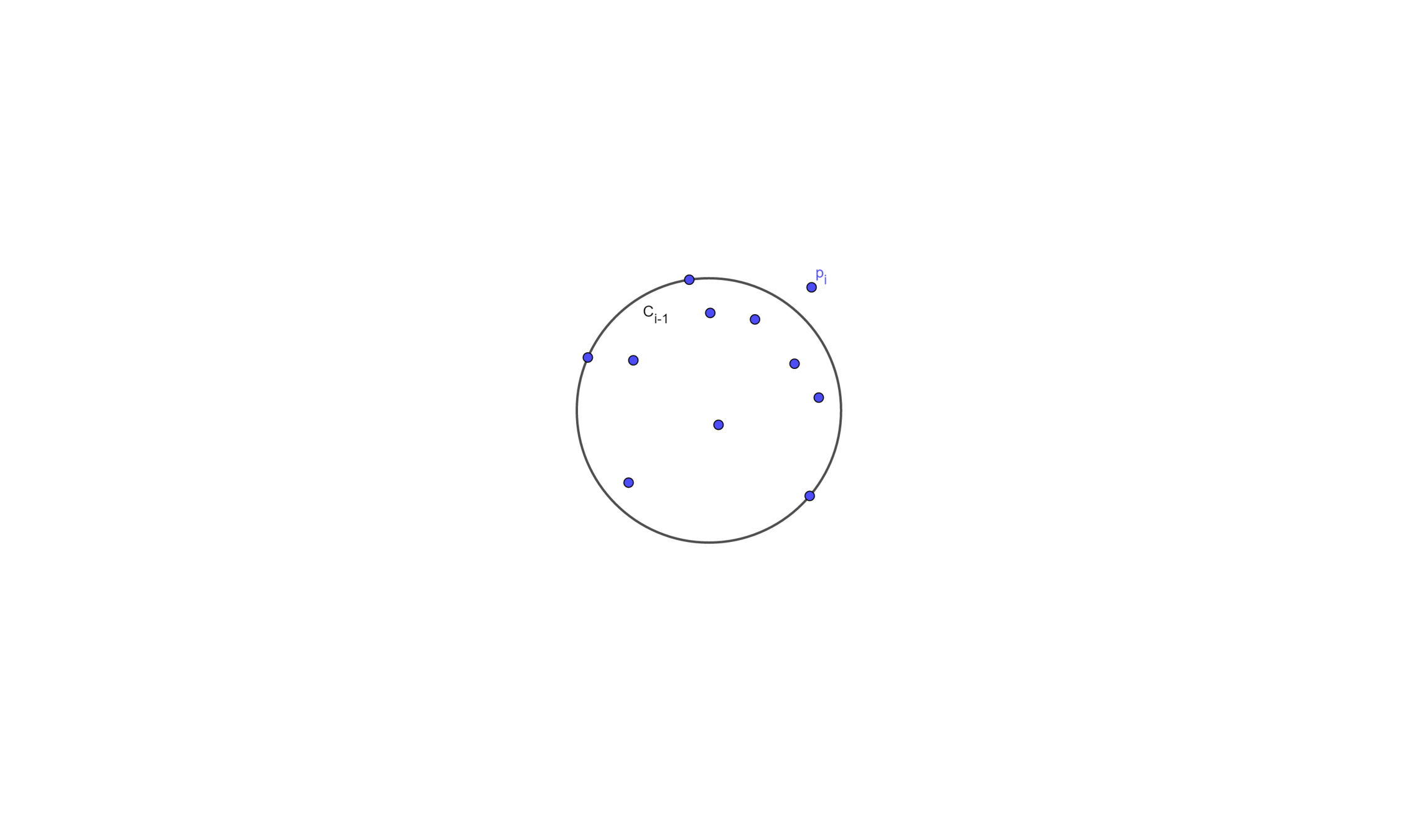
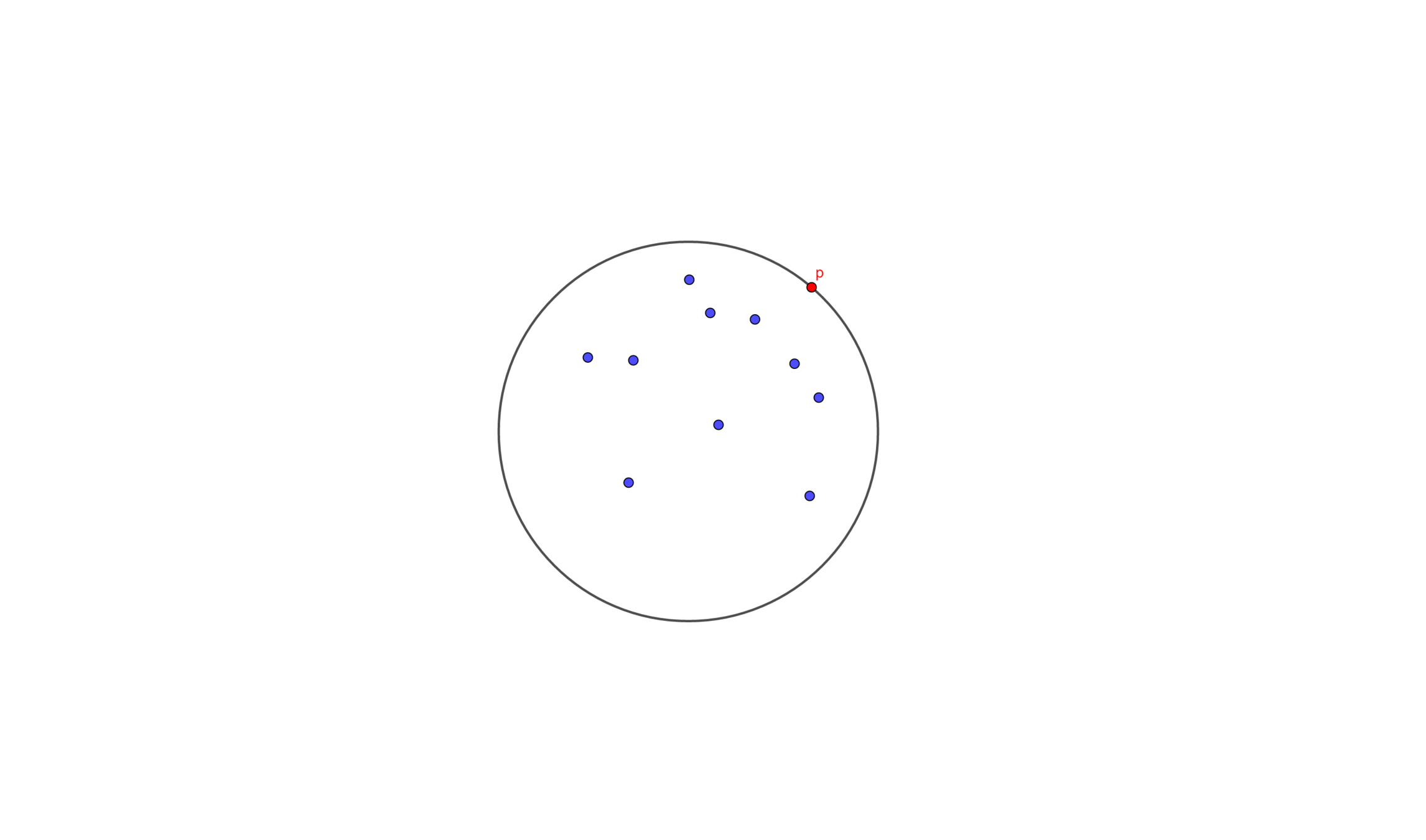
Here comes a new problem

Given a set \(P\) of points and a special point \(p\), determine the smallest enclosing circle of \(P\) that must have \(p\) on the boundary

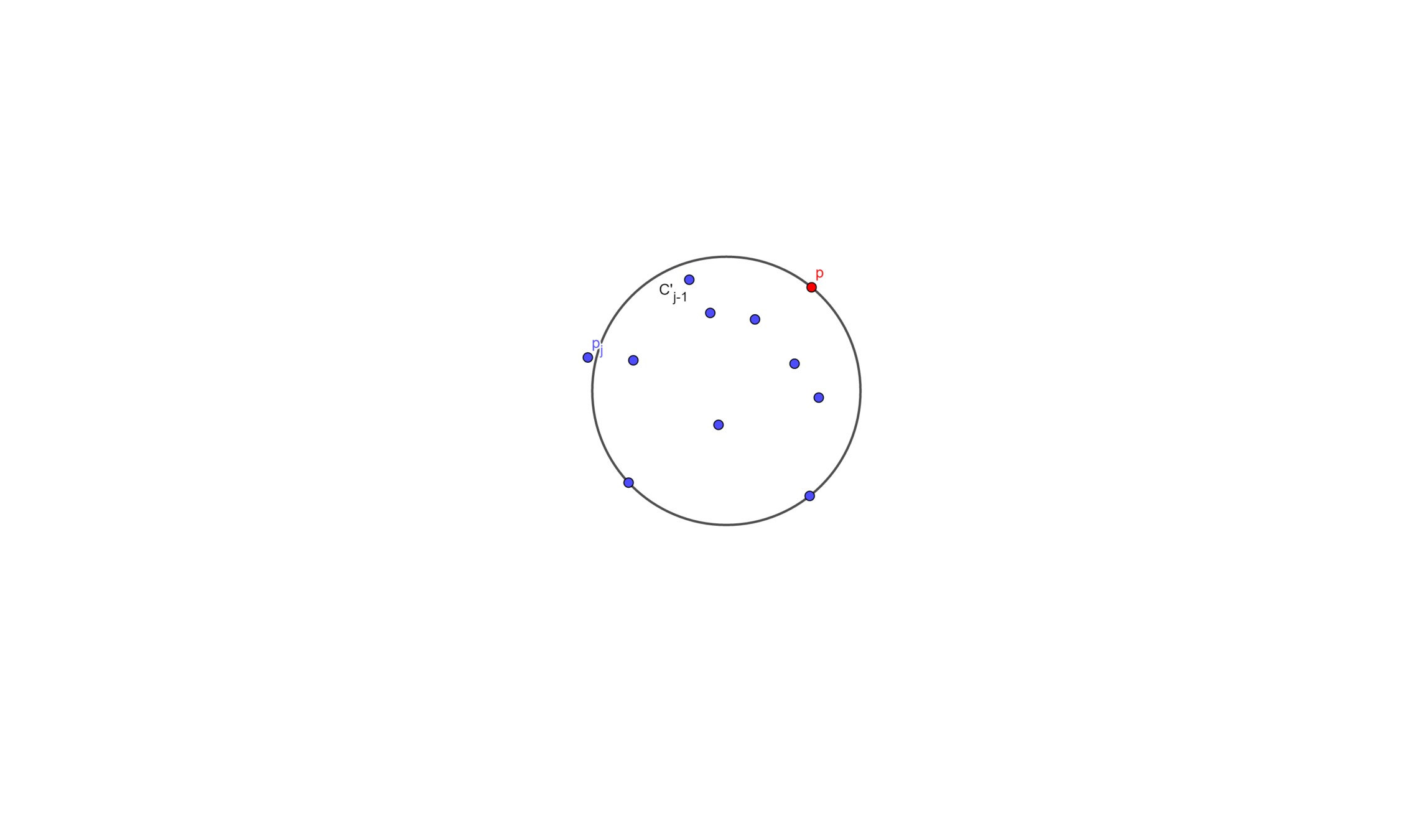
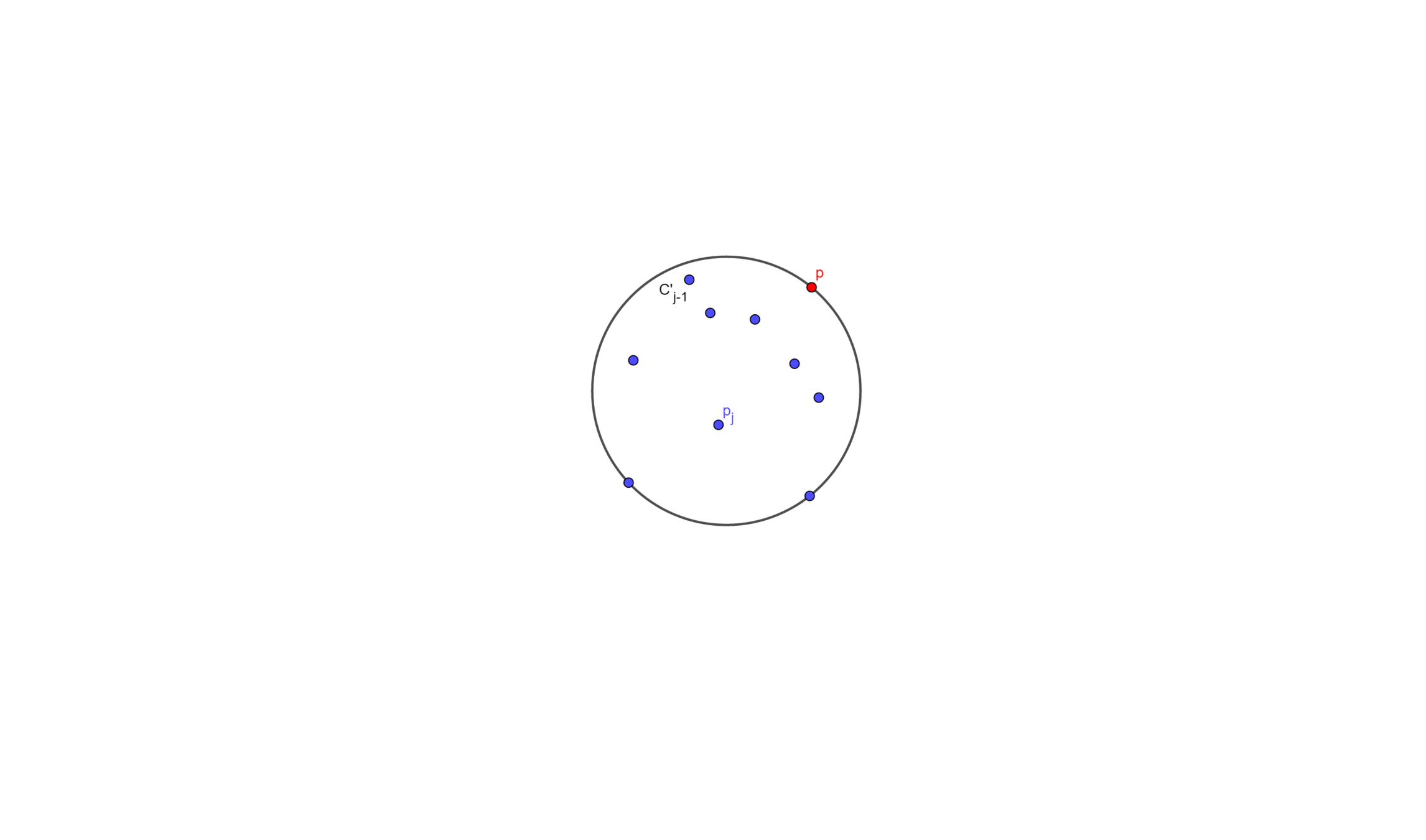
Let \(C'_j\) be the smallest enclosing circle for \(p_1 , \cdots , p_j\) \((j < i)\)and with \(p\) on the boundary

Suppose we know \(C'_{j-1}\), and we wants to add a point \(p_j\)

If \(p_j\) is inside \(C'_{j-1}\), then \(C'_j = C'_{j-1}\)
Else then \(C'_j\) will have \(p_j\) 、 \(p\) on its boundary

Another new problem

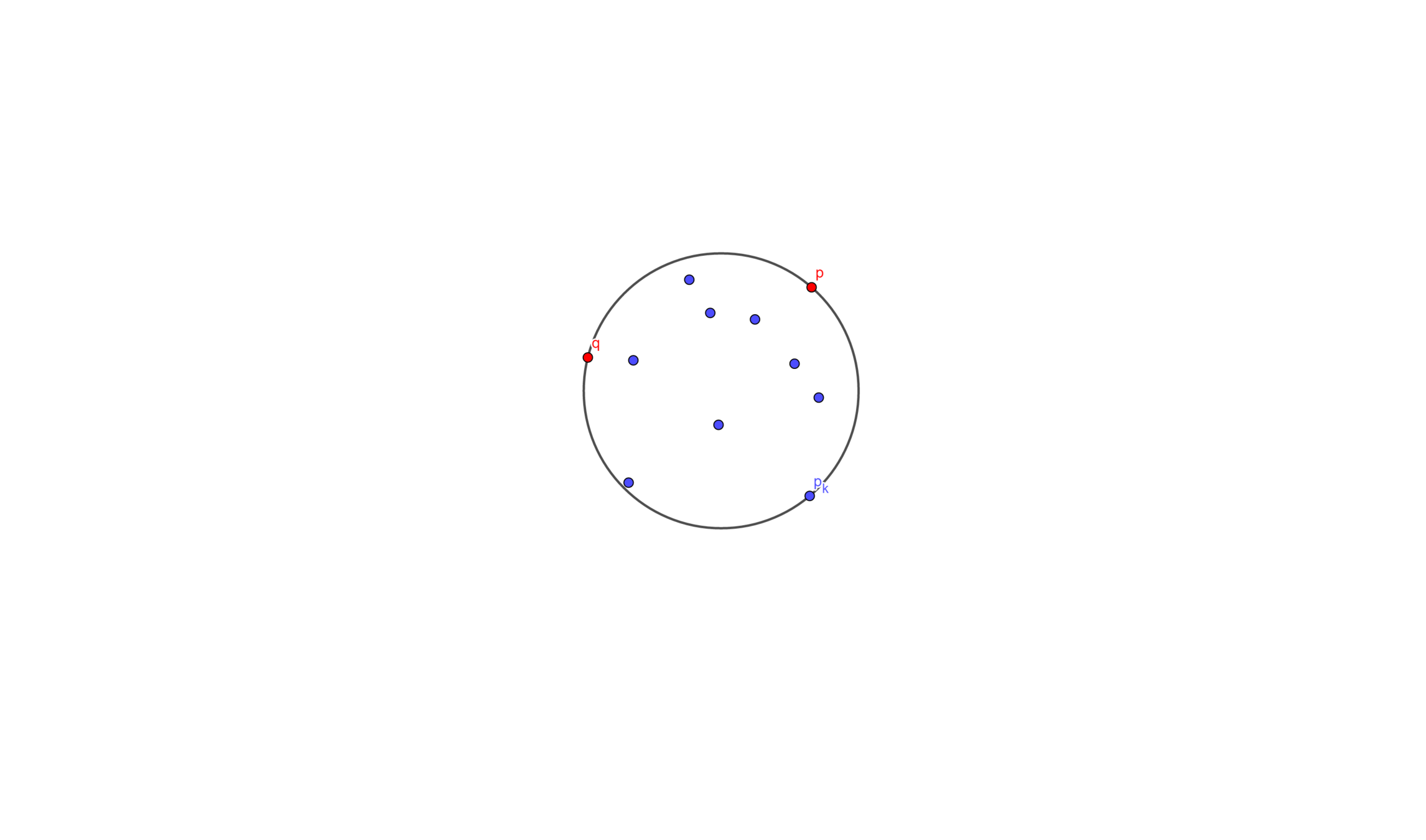
Given a set \(P\) of points and two special points \(p\) and \(q\), determine the smallest enclosing circle of \(P\) that must have \(p\) and \(q\) on the boundary

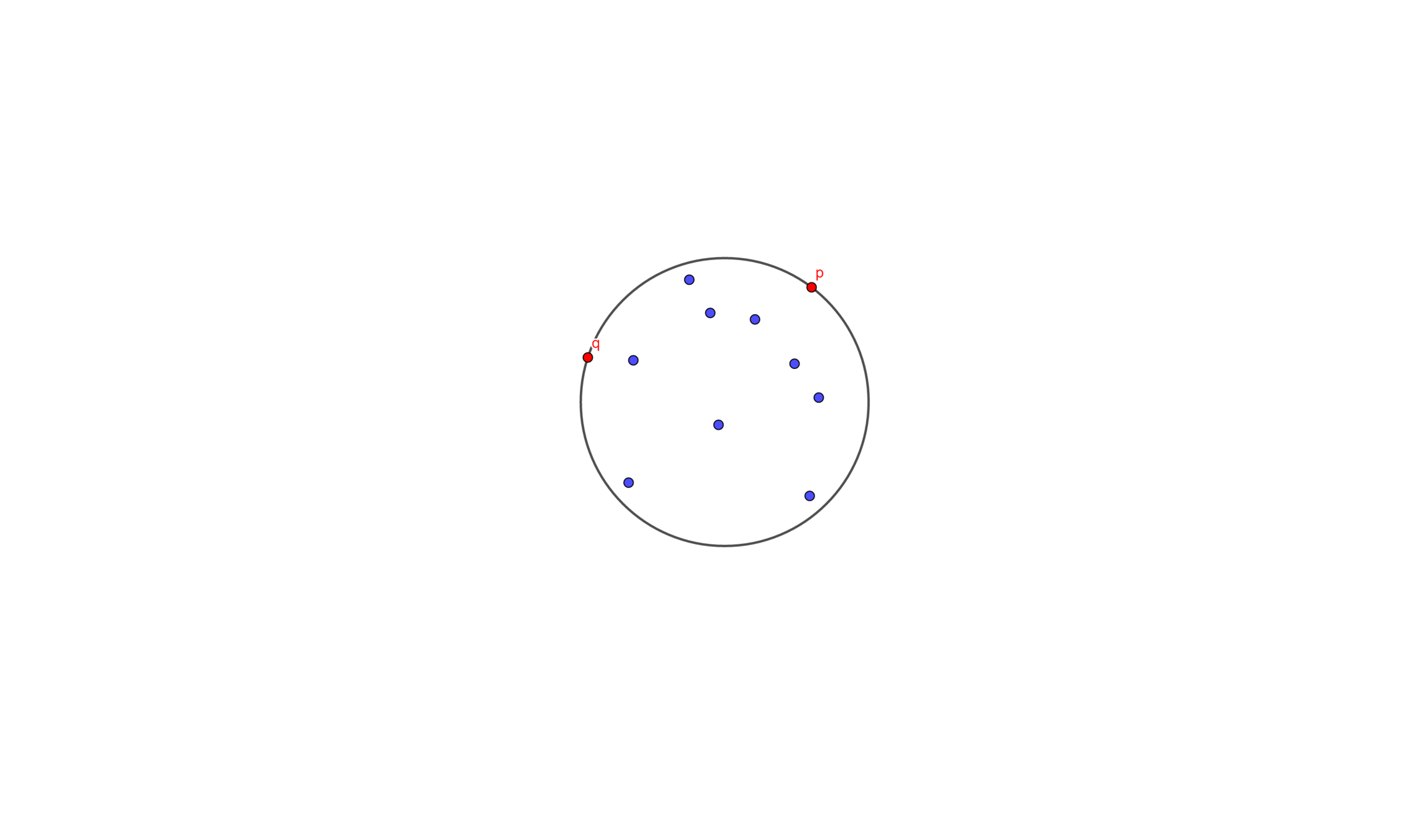
Let \(C'_k\) be the smallest enclosing circle for \(p_1 , \cdots , p_k\) \((k < j)\)and with \(p\) and \(q\) on the boundary

Suppose we know \(C'_{k-1}\), and we wants to add a point \(p_k\)

If \(p_k\) is inside \(C'_{k-1}\), then \(C'_k = C'_{k-1}\)
Else then we take \(p_k\)、\(p\)、\(q\) to make a new circle \(C'_k\) (we know that three point can determine a circle)

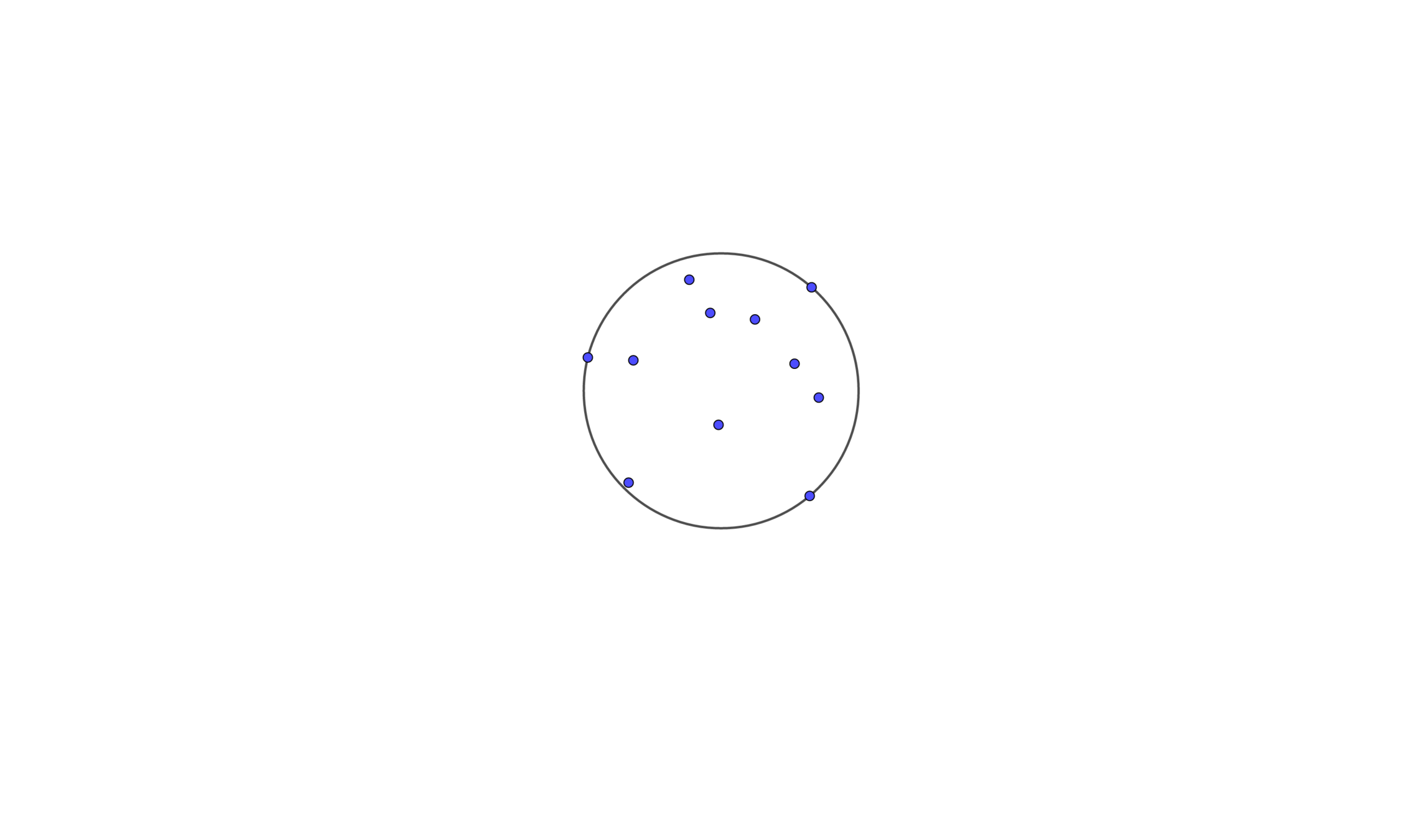
We Find out the Smallest Enclosing Circle

random_shuffle(pts, pts+m);
// Randomize the set of points
init_circle(pts[0], pts[1]);
for (int i = 2; i < n; i++) {
  if (dis(cen, pts[i]) <= rad) continue;
  // p_i isn't inside the circle
  init_circle(pts[0], pts[i]);
  for (int j = 1; j < i; j++) {
    if (dis(cen, pts[j]) <= rad) continue;
    // p_j isn't inside the circle
    init_circle(pts[i], pts[j]);
    for (int k = 0; k < j; k++) {
      if (dis(cen, pts[k]) <= rad) continue;
      // p_k isn't inside the circle
      cen = circumcircle(pts[i], pts[j], pts[k]);
      rad = dis(cen, pts[k]);
    }
  }
}

Time Complexity Analysis

The Smallest Enclosing Circle with a point known

Suppose that we have a circle \(C\) and with \(j\) points added, consider the last point \(j\)

The probability that the point is inside \(C\) is \(\frac{j-3}{j}\), and we need to do nothing for it.

The probability that the point is outside \(C\) is \(\frac{3}{j}\), and we need \(O(N)\) time to solve the subproblem.

The expected time for the j-th addition of a point is

\(\frac{j-3}{j} \times O(1) + \frac{3}{j} \times O(j) = O(1)\)

or \(\frac{j-2}{j} \times O(1) + \frac{2}{j} \times O(j) = O(1)\)

The time complexity of the smallest enclosing circle with a point known is

\(\sum O(1) = O(N)\)

The Smallest Enclosing Circle

Suppose that we have a circle \(C\) and with \(i\) points added, consider the last point \(i\)

The probability that the point is inside \(C\) is \(\frac{i-3}{i}\), and we need to do nothing for it.

The probability that the point is outside \(C\) is \(\frac{3}{i}\), and we need \(O(N)\) time to solve the subproblem.

The expected time for the i-th addition of a point is

\(\frac{i-3}{i} \times O(1) + \frac{3}{i} \times O(i) = O(1)\)

or \(\frac{i-2}{i} \times O(1) + \frac{2}{i} \times O(i) = O(1)\)

The total time complexity is