Tree
課程內容
- 最近共同祖先(LCA)
- 樹練剖分(簡單帶過)
- 啟發式合併
- 樹重心、重心剖分
- 一些有趣的題目
最近共同祖先(LCA)
Before Start ...
為了確保等一下有人聽得懂我講的話
先確認一些基本名詞定義:
圖?樹?森林?
聯通圖?聯通分量?
有根樹?無根樹?
子節點?父節點?
祖先?子樹?
什麼是最低共同祖先?
大波與黑手黨家族
給定一棵包含 \(n\) 個節點的樹,每條邊的長度皆為一,有 \(q\) 筆詢問,每次詢問任意兩節點之間的最低共同祖先
\((n, q \leq 10^6)\)
給一個作法吧,並嘗試估計複雜度
\(O(n^2q)\)?
\(O(nq)\)?
\(O(n log n)\) 作法一:
樹壓平取LCA
歐拉遍歷
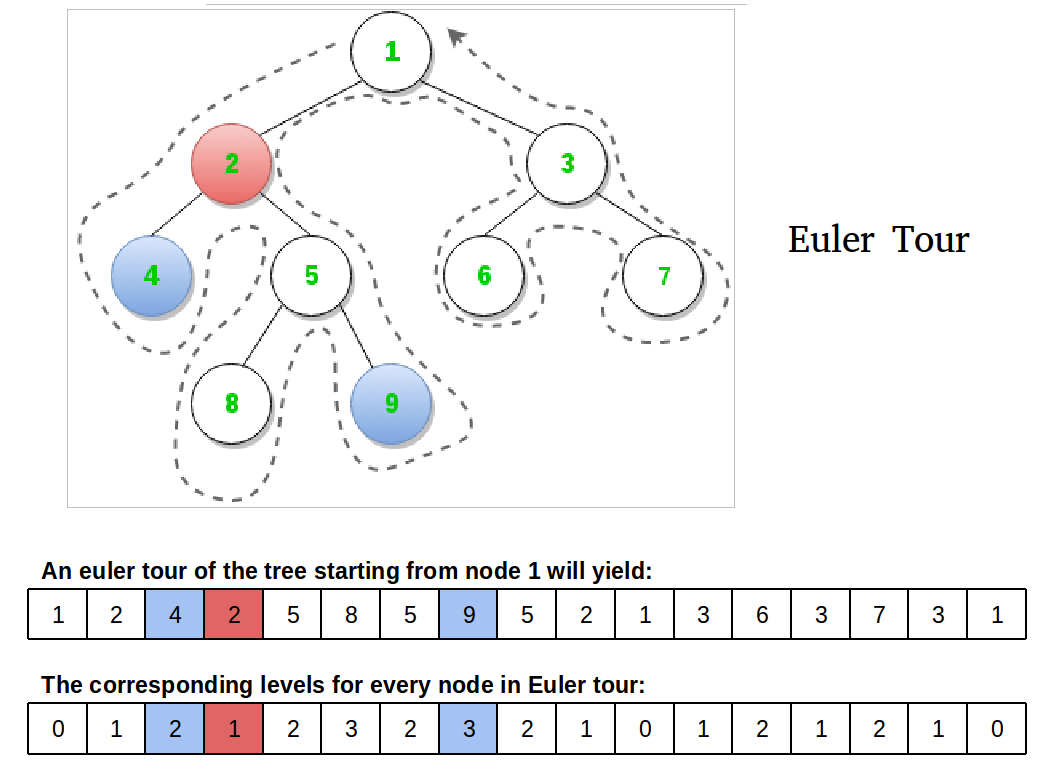
要取得任意兩個節點之間的最低共同祖先,我們只要找他們兩個出現位置之間深度最淺的那個點就行了!
我們可以將點按照深度重新編號
保證讓深度越淺的點有較小的值
搭配區間找最小值的資料結構,我們就可以輕鬆在 \(O(\log n)\) 時間內找到最低共同祖先
總時間複雜度 \(O(n + q \log n)\)
\(O(n log n)\) 作法二:
Doubling倍增法
想像對於每個節點,我們知道他的1倍祖、2倍祖、4倍祖、8倍祖...
我們讓 \(A\) 在不要成為 \(B\) 的祖先的前提下不斷往上跳最大的 2 的冪次
什麼意思?
用上述方法,我們可以找到 \(A\) 深度最淺且不是 \(B\) 的祖先的那個點
而他的父親就是答案!
技術上而言,我們要怎麼知道一個節點的 1倍祖、2倍祖、4倍祖、8倍祖呢?
A 的16倍祖,就是 A 的8倍祖的8倍祖!
物種演化
給定一棵包含 \(n\) 個節點的樹,每條邊的長度皆為一,有 \(q\) 筆詢問,每次詢問任意兩節點之間的路徑長度
\((n \leq 1.5 \cdot 10^4, q \leq 10^6)\)
\(A\) 到 \(B\) 的路徑長度
= \(A\) 的深度 + \(B\) 的深度 - \(LCA(A, B)\) 的深度 * 2
實作時間(?)
樹上最大連續和
給定一棵包含 \(n\) 個節點的樹,邊有邊權,有 \(q\) 筆詢問,每次詢問任意兩節點之間的路徑上最大連續和
\((n, q \leq 2 \cdot 10^5)\)
Graph and Queries
樹鏈剖分
在處理邊的操作與詢問相關問題時,藉由將樹分鏈得到較佳複雜度的算法
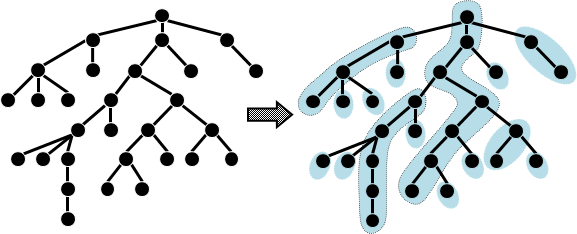
每個點往size最大的子樹連
將樹分解成一條條鏈
- 從一個節點往根的路徑上,只會通過 \(\log N\) 條鏈
- 每次往鏈上的最頂端爬 \(\Rightarrow \log N\) LCA (類似doubling)
int p[maxn],link[maxn],top[maxn],d[maxn];
int getsize(int now=1,int pa=1,int depth=0){
p[now]=pa; d[now]=depth;
int siz=1;
pii maxx{0,0};
for(auto &to:e[now]){
if(to==pa) continue;
int t=getsize(to,now,depth+1);
siz+=t;
maxx=max(maxx,pii{to,t});
}
link[now]=maxx.second;
return siz;
}
void gettop(int now=1,int pa=1,int t=1){
top[now]=t;
if(link[now]!=0) gettop(link[now],now,t);
for(auto &to:e[now])
if(to!=pa&&to!=link[now])
gettop(to,now,to);
}int lca(int a,int b){
while(top[a]!=top[b]){
if(d[top[a]]<d[top[b]]) swap(a,b);
a=p[top[a]];
}
if(d[a]<d[b]) return a;
return b;
}樹鏈剖分、壓平
樹上路徑問題 to 區間問題
按照gettop尋訪順序轉換成序列
- 同一鏈上的節點會依序在相鄰的區間
- 邊往上跳邊加入那個區間的答案
- 利用區間資料結構維護,加速修改查詢
int p[maxn],link[maxn],top[maxn],d[maxn],cnt[maxn];
int getsize(int now=1,int pa=1,int depth=0){
p[now]=pa; d[now]=depth;
int siz=1;
pii maxx{0,0};
for(auto &to:e[now]){
if(to==pa) continue;
int t=getsize(to,now,depth+1);
siz+=t;
maxx=max(maxx,pii{to,t});
}
link[now]=maxx.second;
return siz;
}
void gettop(int now,int pa,int t,int &cnt){
top[now]=t; ind[now]=cnt++;
if(link[now]!=0) gettop(link[now],now,t);
for(auto &to:e[now])
if(to!=pa&&to!=link[now])
gettop(to,now,to);
}
void gettop(int now=1,int pa=1,int t=1,int cnt=0){
int cnt=0; return gettop(now,pa,t,cnt);
}NO Judge
給定一棵樹
支援兩種操作
修改一條路徑上的點權
及查詢兩點間距離
\((N<10^5)\)
void modify(int a,int b,int k){
while(top[a]!=top[b]){
if(d[top[a]]<d[top[b]]) swap(a,b);
add(ind[top[a]],ind[a],k);
a=p[top[a]];
}
if(d[a]<d[b]) swap(a,b);
add(ind[b],ind[a],k);
}
int query(int a,int b){
int tot=0;
while(top[a]!=top[b]){
if(d[top[a]]<d[top[b]]) swap(a,b);
tot+=get(ind[top[a]],ind[a]);
a=p[top[a]];
}
if(d[a]<d[b]) swap(a,b);
tot+=get(ind[b],ind[a]);
return tot;
}給定一個簡單帶權圖
求出刪掉一個邊的最小生成樹最大值
啟發式合併
在處理subtree相關問題時,藉由保留大子樹資訊以得到較佳複雜度的算法
Lomsat gelral
給定一棵以 \(1\) 為根,包含 \(n\) 個節點的樹,每個節點有一個顏色 \(c_i\),求樹中每個子樹出現最多次的顏色編號的和
\((n \leq 10^5)\)
不知道怎麼做的時候,就先想個naive解吧!
我們可以對每個節點用一個map維護每個顏色在該節點子樹中的出現次數
隨便轉移一下,複雜度 \(O(n^2 \log n)\)
不覺得每次轉移上去都要新開一個map來紀錄根本超麻煩嗎==
感覺把最大子樹原本的那個map直接拿上去用會省掉很多麻煩(?
甚至連複雜度都變好了(?!
如果你常常像剛才那樣不小心換一個方法做突然就從TLE變AC的話,請保持你的通靈感,你已經具備了唬爛進1!、2!、3!的潛力><
回歸正題,如果你照著剛剛那個方法做,複雜度就會是好好的 \(O(n \log ^2 n )\) 了,AC~~
But why???
照著剛剛的那個方法,考慮每一個節點需要被提出來合併的次數:當該節點所在的子樹不是其父親的最大子樹時,就需要被提出來合併,我們稱這種子樹的根為輕點
回想一下樹練剖分,一個節點到根的路徑中,至多不會超過 \(\log n\) 個輕邊,意即輕點數量也同樣不超過 \(\log n\)
每個點不合併超過 \( \log n\) 次,每次對map的操作為 \( \log n\),得總複雜度 \((n \log ^2 n)\)
DSU 查詢複雜度
\(O(1)\)、\(O(\log n)\)、\(O(\alpha (n) )\) ?
| 路徑壓縮 | ||
| 啟發式合併 | ||
\(O( \alpha (n) )\)
\(O( \log n )\)
\(O( \log_{2+f/n} n ) \)
\(O( n )\)
補充額外冷知識(但講師不會證明QAQ
忍者調度問題
給定一棵以 \(1\) 為根,包含 \(n\) 個節點的樹以及預算上限 \(M\),每個節點(忍者)分別有出動費用 \(C_i\) 和領導力值 \(L_i\),假設以節點 \(i\) 為領導者,其所能造成的滿意度是
\(L_i \times\) (在預算內能在其子樹內出動的最多忍者數量)
請求出在預算內能夠達到的最大滿意度
\((n \leq 10^5, M \leq 10^9)\)
Blood Cousins
給定一座包含 \(n\) 個節點的森林,接著是 \(m\) 筆詢問,每次詢問一個點與多少個點擁有共同的 \(K\) 倍祖先
\((n, m \leq 10^5)\)
Dominant Indices
給定一棵以 \(1\) 為根,包含 \(n\) 個節點的樹
設 \(d(u, x)\) 為 \(u\) 子樹中到 \(u\) 距離為 \(x\) 的節點數。 對於每個點,求一個最小的 \(k\),使得 \(d(u, k)\) 最大。
\((n \leq 10^6)\)
重心剖分
在一棵大小為 \(n\) 的樹上,找到一個點,移除後使得留下的所有連通分量(樹)的大小均不超過 \(\frac{n}{2}\),那麽這個點就是整棵樹的重心
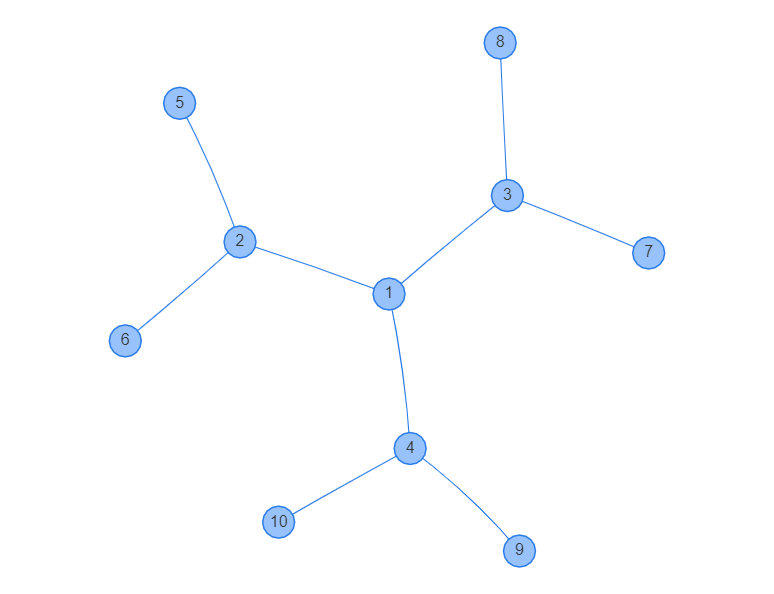
一棵樹至少有幾個重心?至多呢?
要怎麼找到樹的重心?\(O(n)\)
一棵樹至少有 1 個重心,至多則為 2 個,且這兩個重心必相鄰
首先任取節點 \(a\),以 \(a\) 為樹的根,計算它所有子樹的大小。如果這些子樹的大小均不超過 \(\frac{n}{2}\),則 \(a\) 就是重心。否則,必然存在一棵子樹,大小超過 \(\frac{n}{2}\),於是我們對其重複上述算法,最終即可找到重心。
複雜度?
重心剖分?
一棵樹的重心剖分會用另外一棵樹來表示
以遞迴定義:
樹根為其重心
每個子樹代表拔掉重心後的各個連通分量
怎麼做?
喔 其實直接照定義建樹就好了耶
那複雜度是多少呢?
其實跟 merge sort 的複雜度分析很像><
Xenia and Tree
給定一棵以 \(1\) 為根,包含 \(n\) 個節點的樹,一開始每個節點皆為藍色,接下來有 \(q\) 筆操作,操作分為兩種,一種是將一個點塗成紅色,另一種則是詢問一個點與距離他最近的紅點之距離
\((n, q \leq 10^5)\)
實作時間(?)
Ciel the Commander
給定一棵包含 \(n\) 個節點的樹,要求把上面的所有節點用 A 到 Z 標記,使得對於任意兩個標記相同的節點,它們之間的最短路上至少有一個標記(字典序)更小的節點。
\((n \leq 10^5)\)
橘子園保衛戰
給定一棵包含 \(n\) 個節點的樹,要求把上面的所有節點用 A 到 Z 標記,使得對於任意兩個標記相同的節點,它們之間的最短路上至少有一個標記(字典序)更小的節點。
\((n \leq 10^5)\)
Centroids
烏龜埋伏
乘數與被乘樹
更多題目
Roads in the Kingdom
給定一棵包含 \(n\) 條邊(邊有邊權)的聯通圖,求刪掉一條邊所形成的樹中,所能夠產生的最小直徑。
\((n \leq 2 \cdot 10^5)\)
Beautiful Road
Arch
Disruption
Cat in a tree
烏龜暗殺
樹莫隊
NO Judge
給定一棵樹
每個節點一個顏色
對於 \(q\) 筆詢問 \(a_i,b_i\)
回答節點 \(a_i,b_i\) 之間路徑上顏色的眾數數量
\((n,q<5\times10^4)\)
眾數=>莫隊?
樹莫隊
- 壓平
- 詢問轉換
- 正常莫隊!
1. Euler Tour Flattening
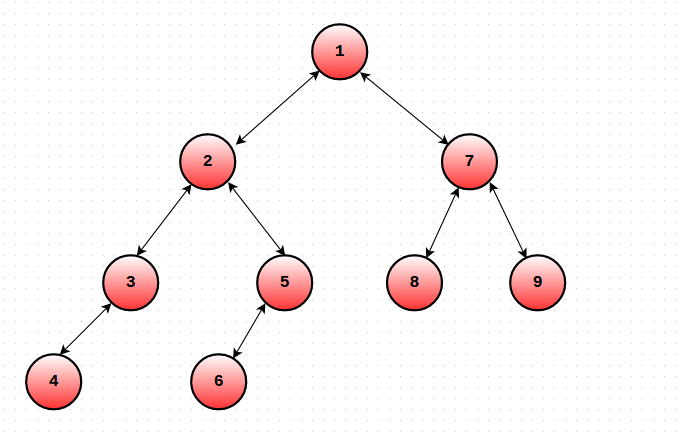
Euler Tour Order:
2. Query transformatiom
兩點間路徑轉換成序列?
- XOR 抵銷「進去」又「出來」的節點
兩點間路徑轉換成序列?
- XOR 抵銷「進去」又「出來」的節點
Case 1
Case 2
\(a=lca(b)\)
假設 \(start(a)<start(b)\)
\(query(a,b)=[start(a),start(b)]\)
\(a\ne lca(b)\)
\(query(a,b)=[end(a),start(b)]+start(lca(a,b))\)