Skewed Mirror Symmetry in the 3D Reconstruction of Polyhedral

 Models

prepared by Ceren Altunal Podlech

INTRODUCTION

Goal: Geometrical or perceptual information automatically from a sketch or two dimensional line drawings.

It is difficult to formulate visual geometry in algorithmic terms

 

break into smaller elements

(perceptive cues/features)

Method: Determining axes of facial symmetry

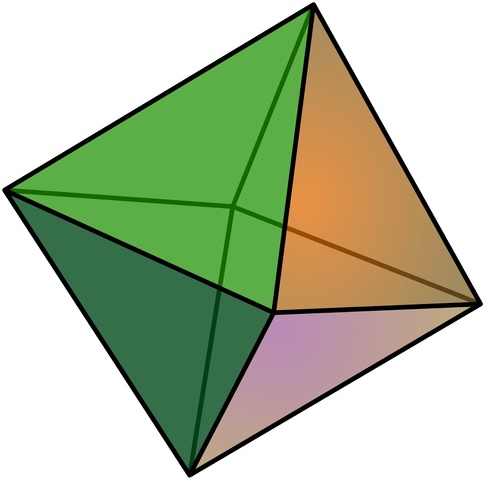
"A skewed symmetry depicts a real symmetry viewed from someone (unknown) view direction"

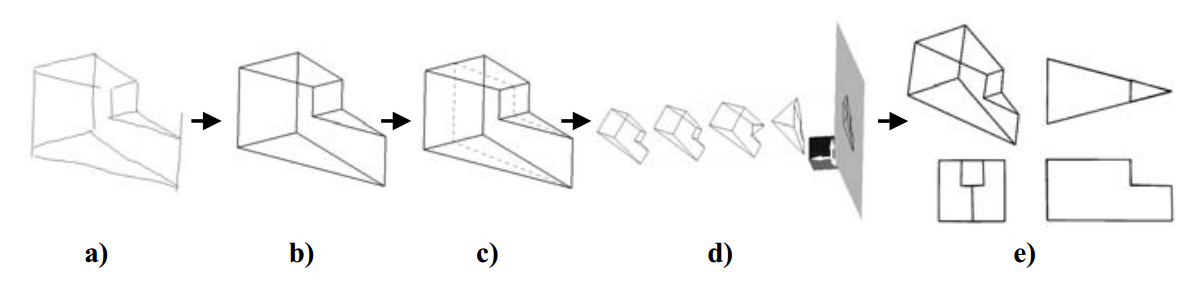
  • Improve the reconstruction process.
  • Applying symmetry as a regularity in optimisation-based reconstruction is shown to be adequate by itself, without the need for other inflation techniques or regularities.
  • Furthermore, symmetry can be used to reduce the size of the reconstruction problem, leading to a reduction in computing time.

Why Skewed symmetry is important?

DETECTION OF FACES

Detection of skews facial symmetry requires the prior determination of the faces of the two-dimensional image.

Complex problem

Because, the faces of a polyhedron are
projected as polygons,

 

they intersect
each other where the projections of the visible and
hidden faces overlap

Under development method:


Automatic determination in two dimensions of faces of polyhedral objects represented by an axonometric projection or conic perspective.

Base on graph theory and perceptual cues.



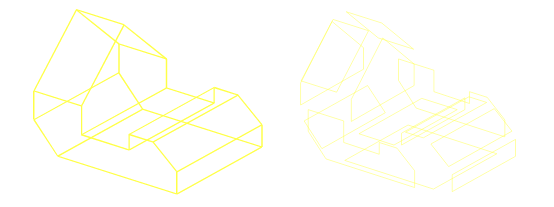
after detecting the surface, we can find the possible axes of symmetry for each face

 Facial Symmetry

Mirror symmetry in 2D is determined by an axis lying
in the plane of the figure that divides it in two parts,
such that for each point on one of the parts, there is a
corresponding point on the other

Skewed facial symmetry occurs when,

after carrying out a parallel projection of a symmetric polyhedral object,

 

Certain faces have one or more axes that divide them into two parts such that for each point on one of the two parts there is a
corresponding point on the other,

 

Both points must be equidistant from the axis

determine a straight line making a conjugate direction to the axis.

 

This conjugate direction is the same for all points on a given face. The conjugate direction is the projection of the direction orthogonal to the un-projected symmetry axis.

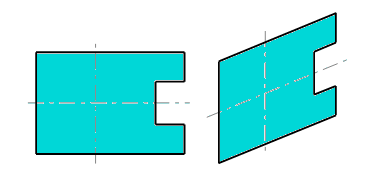
Skewed Facial Symmetry

A set of points in the Euclidean plane has skewed symmetry if an axis of skewed symmetry and  a fixed angle such that object invariant under the transformation.

\alpha=arctan\left[ \frac{\sum_{N}^{i=1}x_{i}y_{i}tan\gamma - \sum_{N}^{i=1}y_{i}^{2}}{\sum_{N}^{i=1} x_{i}^{2}tan\gamma-\sum_{i=1}^{N} x_{i} y_{i}}\right]
α=arctan[∑Ni=1xiyitanγ−∑Ni=1yi2∑Ni=1xi2tanγ−∑i=1Nxiyi]\alpha=arctan\left[ \frac{\sum_{N}^{i=1}x_{i}y_{i}tan\gamma - \sum_{N}^{i=1}y_{i}^{2}}{\sum_{N}^{i=1} x_{i}^{2}tan\gamma-\sum_{i=1}^{N} x_{i} y_{i}}\right]
\gamma=arctan \left[ \frac{ \sum_{N}^{i=1}\frac{y_{i}^{2}}{tan\alpha} - \sum_{N}^{i=1}x_{i}y_{i} }{ \sum_{N}^{i=1}\frac{x_{i}y_{i}}{tan\alpha} - \sum_{i=1}^{N} x_{i}^{2} } \right]
γ=arctan[∑Ni=1yi2tanα−∑Ni=1xiyi∑Ni=1xiyitanα−∑i=1Nxi2]\gamma=arctan \left[ \frac{ \sum_{N}^{i=1}\frac{y_{i}^{2}}{tan\alpha} - \sum_{N}^{i=1}x_{i}y_{i} }{ \sum_{N}^{i=1}\frac{x_{i}y_{i}}{tan\alpha} - \sum_{i=1}^{N} x_{i}^{2} } \right]
P \cdot T=Q
P⋅T=QP \cdot T=Q
P=[x,y]
P=[x,y]P=[x,y]
Q=[u,v]
Q=[u,v]Q=[u,v]

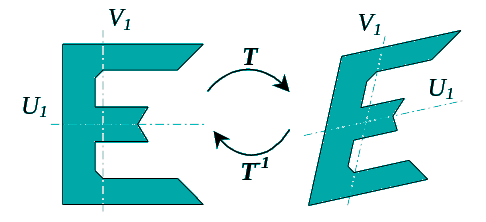
Fundamental Condition of Symmetry

Cartesian and skewed coordinates

Q=T^{-1}P
Q=T−1PQ=T^{-1}P

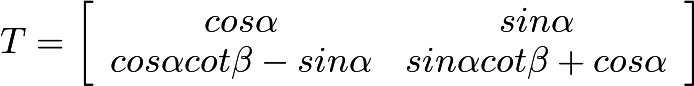
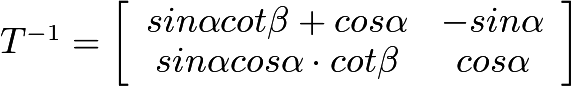
       skewing function

             deskewing function

T^{-1}
T−1T^{-1}
T
TT

Detecting Skewed Facial Symmetry for Simple Polyhedra

centroid (c), used as origin of the coordinates.

The process for determining skewed facial symmetry

  • A face is chosen and its centroid is calculated
  • Some vertex (or edge mid point) is chosen which determines the candidate axis
  • A possible axis of symmetry and its conjugate direction
  • Using  alpha and gamma calculation of             and apply it to all vertexes of the contour.
  • We check whether the resulting face has mirror symmetry.
T^{-1}
T−1T^{-1}
\sum_{i=0}^{N-1} x_{i}y_{i} = 0
∑i=0N−1xiyi=0\sum_{i=0}^{N-1} x_{i}y_{i} = 0

not sufficient!

Condition of Total Symmetry

k is the (cyclically numbered) vertex or edge mid-point the axis of symmetry passes through

i= [1, 2, ..., n /2]


 is formulated in such a way that, if the figure is symmetric after the transformation, it will also be symmetric with
respect to the X axis.

T^{-1}
T−1T^{-1}
x_{i-k}=x_{i+k}
xi−k=xi+kx_{i-k}=x_{i+k}
y_{i+k}+y_{i-k}=0
yi+k+yi−k=0y_{i+k}+y_{i-k}=0

PLANES OF SYMMETRY IN POLYHEDRA

Three main rule

1

When a symmetry axis across a face ends in the mid-point of an edge,

the opposing face on the other side of the edge

 

must also have an axis ending in the mid-point of this edge.

2

Axes of symmetry of a face going through a vertex can continue along an edge or another axis of symmetry.

However, two consecutive lines must not belong to the same face.

 

 

 

3

Must be  a closed chain of lines!
A line connecting both vertices
( v1 and v2 ) must be present for that face

if l1 and l2 do belong to a symmetry plane.

 

Suppose two consecutive candidate

lines l1 and l2 have vertices v1 and v , and v and v2 .

Suppose furthermore that v 1 and v 2 belong to the same face.

 

Can axes l1 and l2 can not belong to a
single symmetry plane?

no line between v1 and v2 on the face to which they both belong.

LIMITS IN SERCH FOR PLANES OF SYMETRY

Method for searching for
planes of symmetry in two-dimensional graphs
depends directly on the correct detection of faces in a
graph, and correct detection of axes of facial
symmetry on them.

Eliminate further candidate axes for
planes of symmetry it can eliminate some real
planes of symmetry. However, the method
detects all relevant and most important planes of
symmetry

The method does not find
planes of symmetry that consist exclusively of edges
of the polyhedron. 

CONCLUSION

Detected skewed planes of symmetry

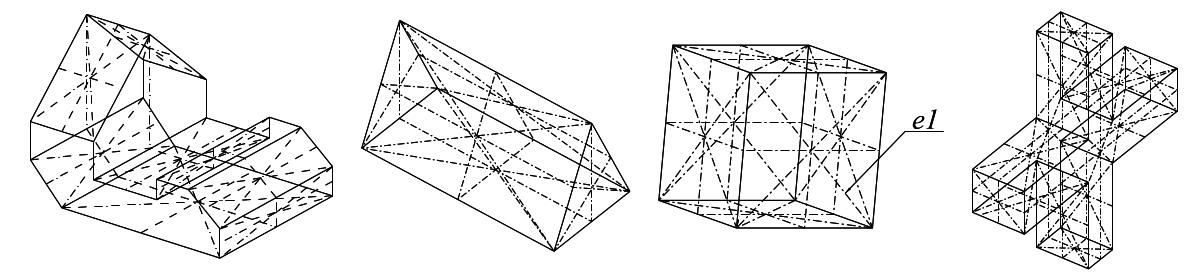
Each face has all its axes of skewed symmetry detected

Thank You!

Made with Slides.com