data-driven simulation-based galaxy evolution


Yale galaxy lunch --- Nov 20, 2019
ChangHoon Hahn
arXiv:1809,01665
arXiv:1910.01644
everything we've learned so far from galaxy surveys
... in 30 sec
* about massive galaxies at z<2
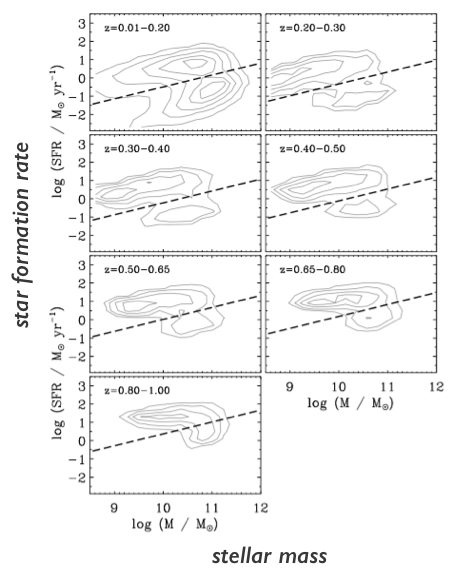
galaxies broadly fall into two categories

star forming galaxies
late-type, disk-like, blue

quiescent galaxies
early-type, elliptical, red
PRIMUS
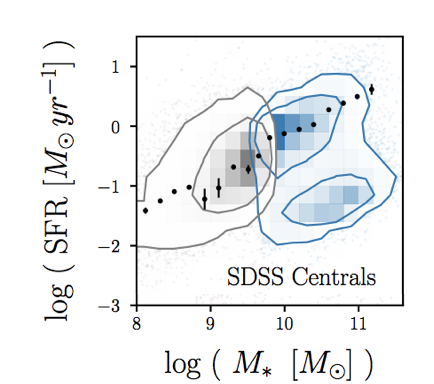
star-forming galaxies lie on the star-forming sequence
Hahn+(2019a)
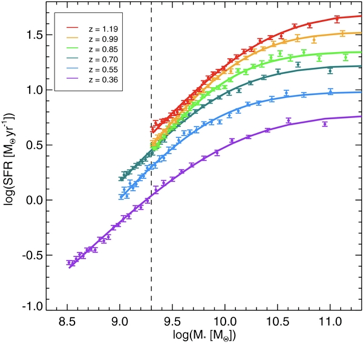
overall decline in star formation over time
Lee+(2015)
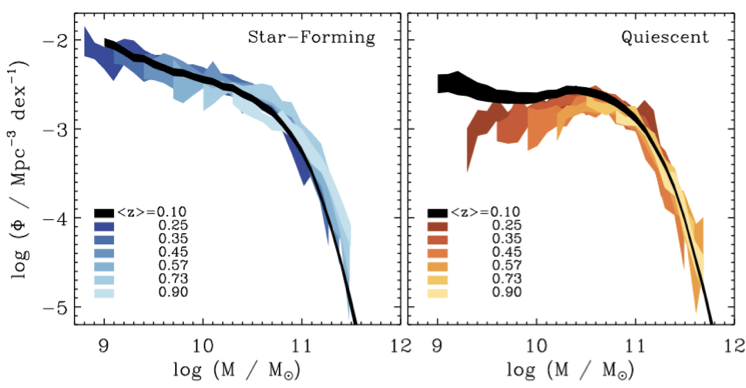
fewer massive star-forming galaxies
more quiescent galaxies over time
Moustakas+(2013)
PRIMUS
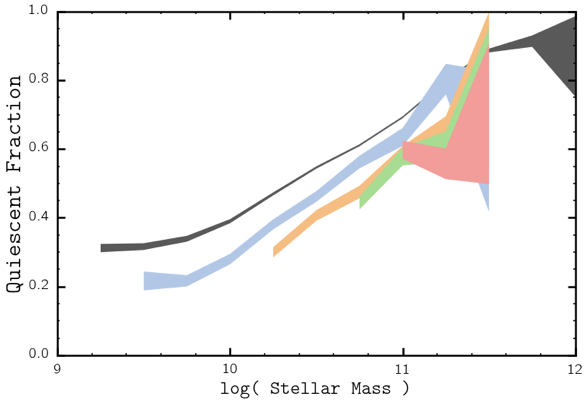
log (stellar mass)
quiescent fraction
SDSS z~0
PRIMUS z~0.9
state-of-the-art galaxy formation models roughly reproduce these relations
credit: Illustris TNG
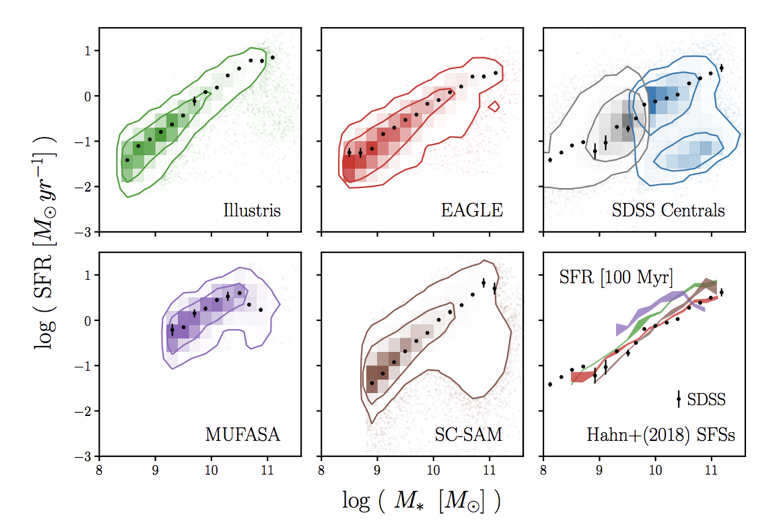
simulations can produce the star-forming sequence (SFS)
Hahn+(2019a)
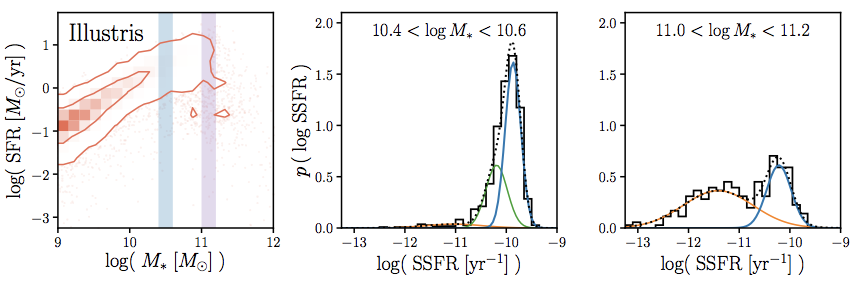
data-driven GMM-based method for identifying the
star-forming sequence
Hahn+(2019a)
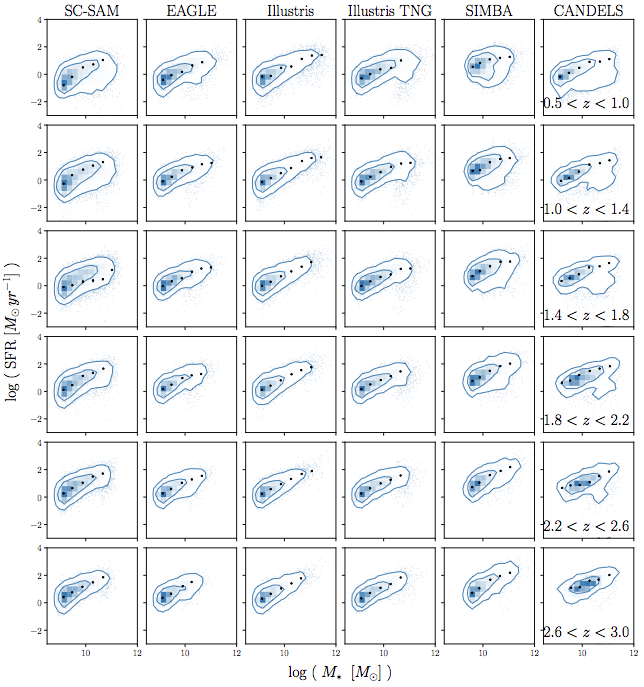
out to high redshifts
Choi, CH+(in prep)
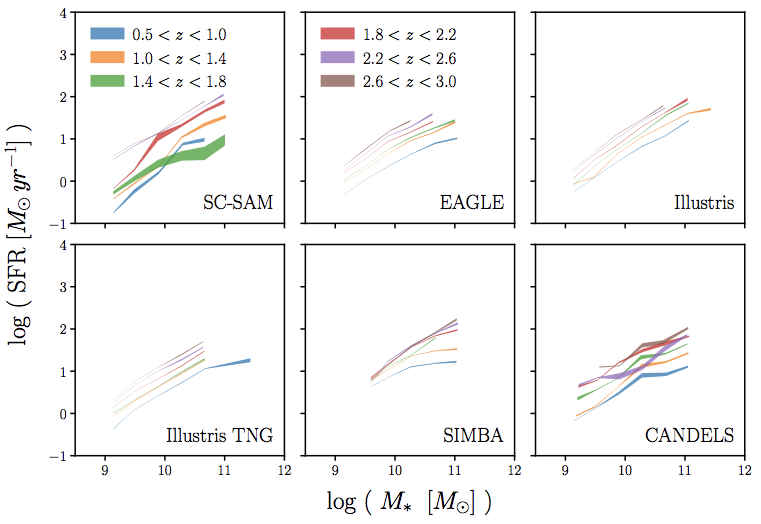
Choi, CH+(in prep)
*...don't worry about SC-SAM
they can also produce the SFS z evolution
can we make galaxy formation/evolution into an inference problem?
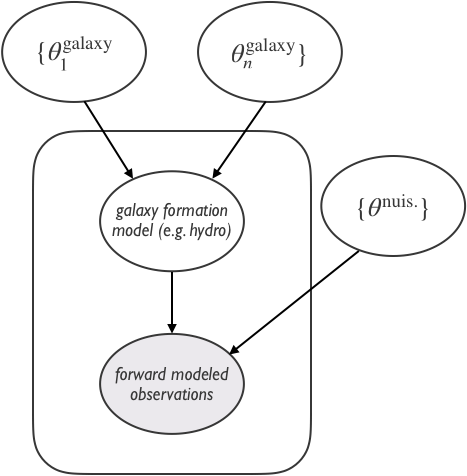
Isolated and Quenched collaboratory: framework for forward modeling observations
computational expensive*
... not easy to interpret
e.g. why do SFS in simulations differ by ~5x?
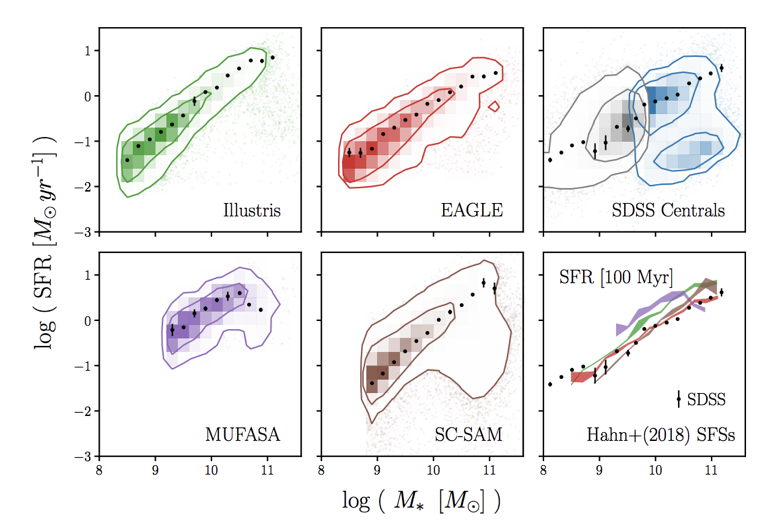
Hahn+(2019a)
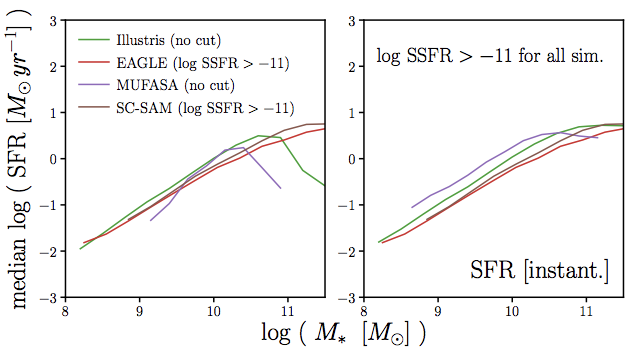

same methods as Somerville & Davé (2015)
why we need data-driven methods
empirical models: ΛCDM + observed evolution of galaxies
credit: Wechsler & Tinker (2018)
computationally cheap
easy to interpret
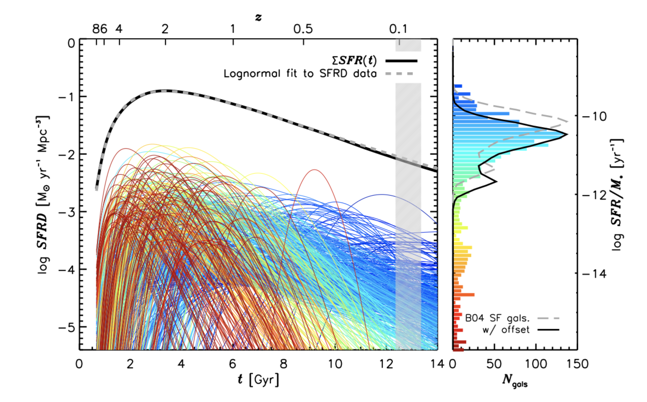
Abramson+(2015, 2016)
their claim: loosely constrained log-normal SFH can reproduce SMF, SFS, etc. at z<6

they get stellar masses from the star formation histories but ...what about the stellar-to-halo mass relation?
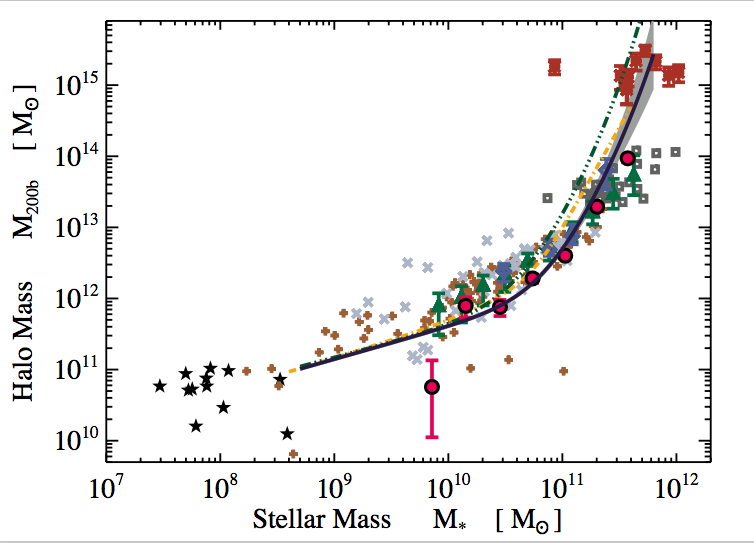
credit: Alexie Leauthaud
for star forming central galaxies
the connection between star formation histories and stellar masses constrained by star forming sequence
the stellar-to-halo mass relation constrains the connection between stellar masses and halo mass
we can constrain star formation histories using the
star-forming sequence and stellar-to-halo mass relation!
star-forming centrals initialized using SMF and SFS at z~1
M* from subhalo-halo abundance matching to SMF
SFR from SFS with 0.3 dex scatter
once quenched always quenched
the connection between star formation histories and stellar masses constrained by star forming sequence
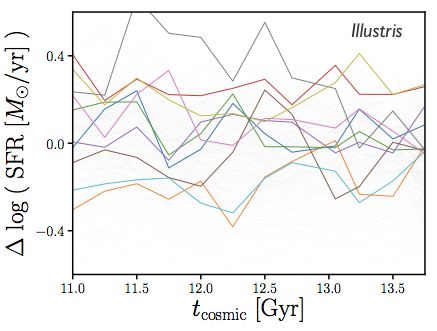
star-forming centrals in Illustris
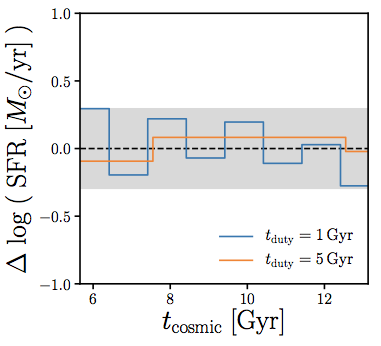
star formation duty cycle: star formation histories that vary on tduty Gyr timescales
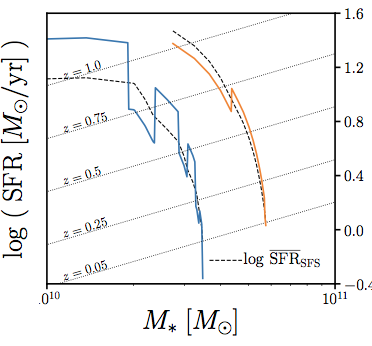
models that reproduce* SMF and SFS at z~0
but have different tduty
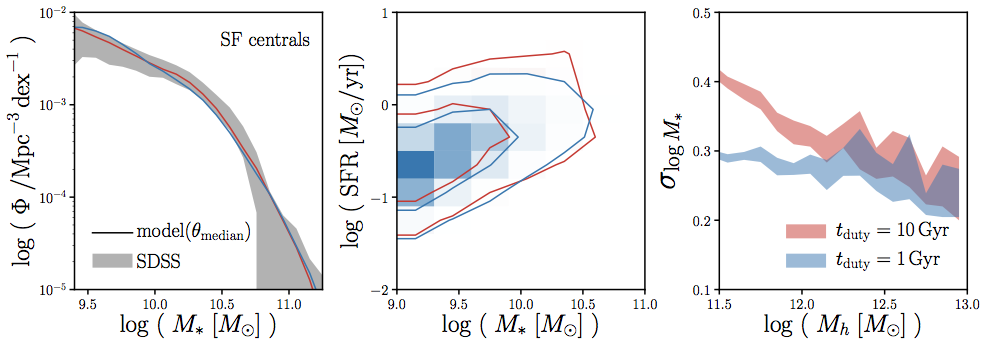
*using Approximate Bayesian Computation (more on this later!)
predict different scatter in SHMR
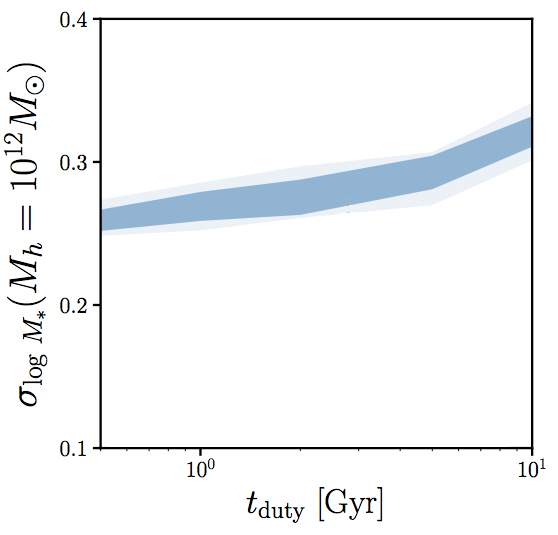
scatter in SHMR at low Mh is sensitive to tduty (i.e. timescale of SF variability)
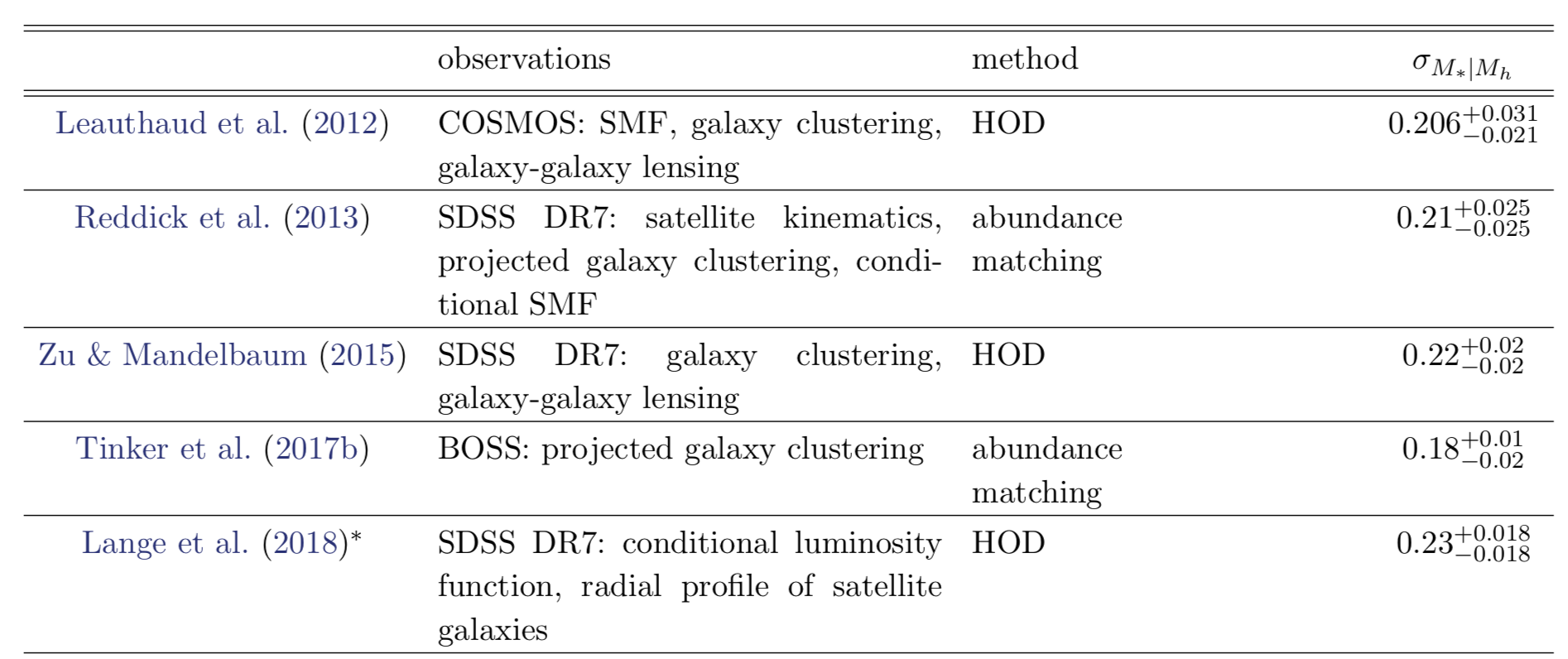
observations find a tight ~0.2 dex scatter in SHMR

we add galaxy assembly bias to our model:
star formation histories correlate with Mh history
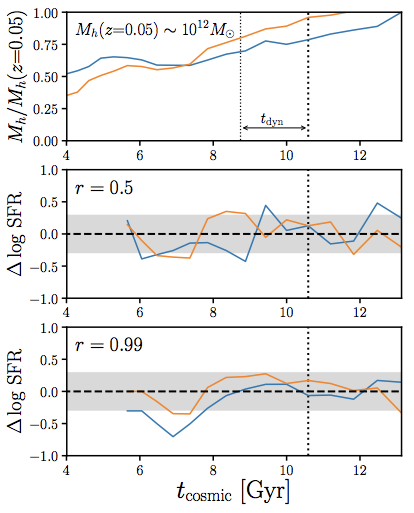
similar to Rodríguez-Pubela+(2016), Behroozi+(2019)
correlated to
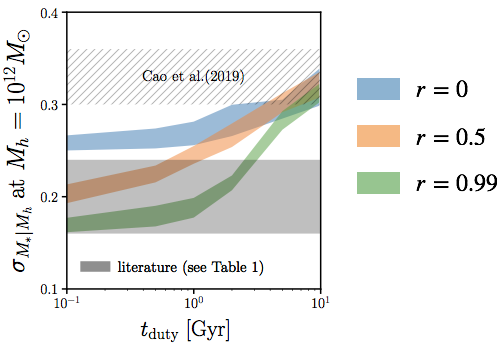
tighter scatter in SHMR for stronger galaxy assembly bias
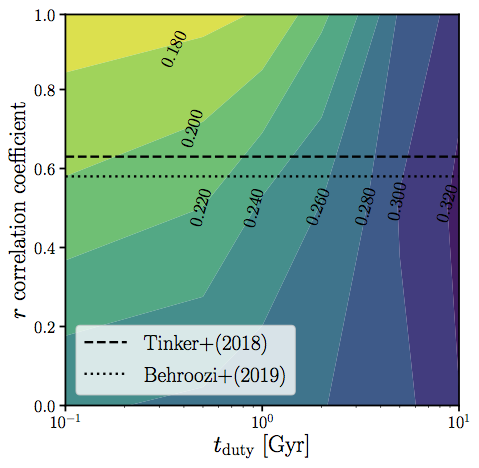
scatter in SHMR sensitive to tduty and rassembly bias
r~0.6 from literature ... tduty < 0.2 Gyr ?

new constraints find larger SHMR >0.3dex scatter

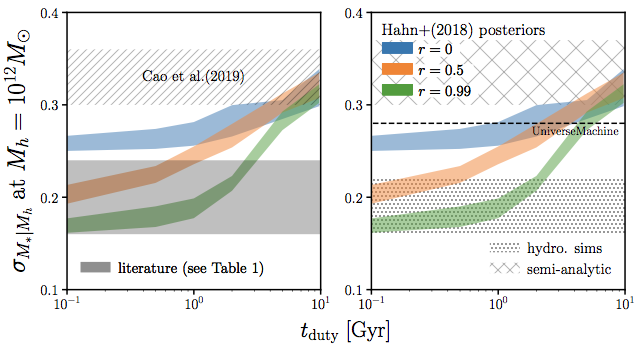
also no consensus among simulations
tight constraint on tduty currently limited by tensions in both observations and simulations
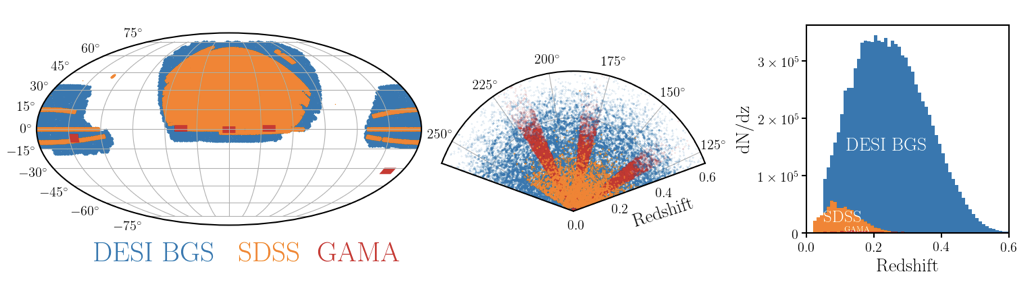
DESI Bright Galaxy Survey
14,000 sq.deg
magnitude-limited to r~20
10 million galaxies

DESI first light!
<1% sky subtraction
the PRObabilistic Value-Added BGS
(PROVABGS)
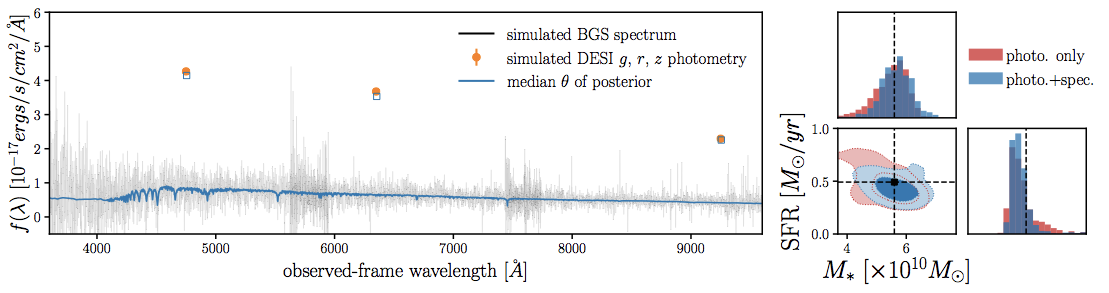
10 million posteriors of galaxy properties from jointly fitting photometry+spectroscopy
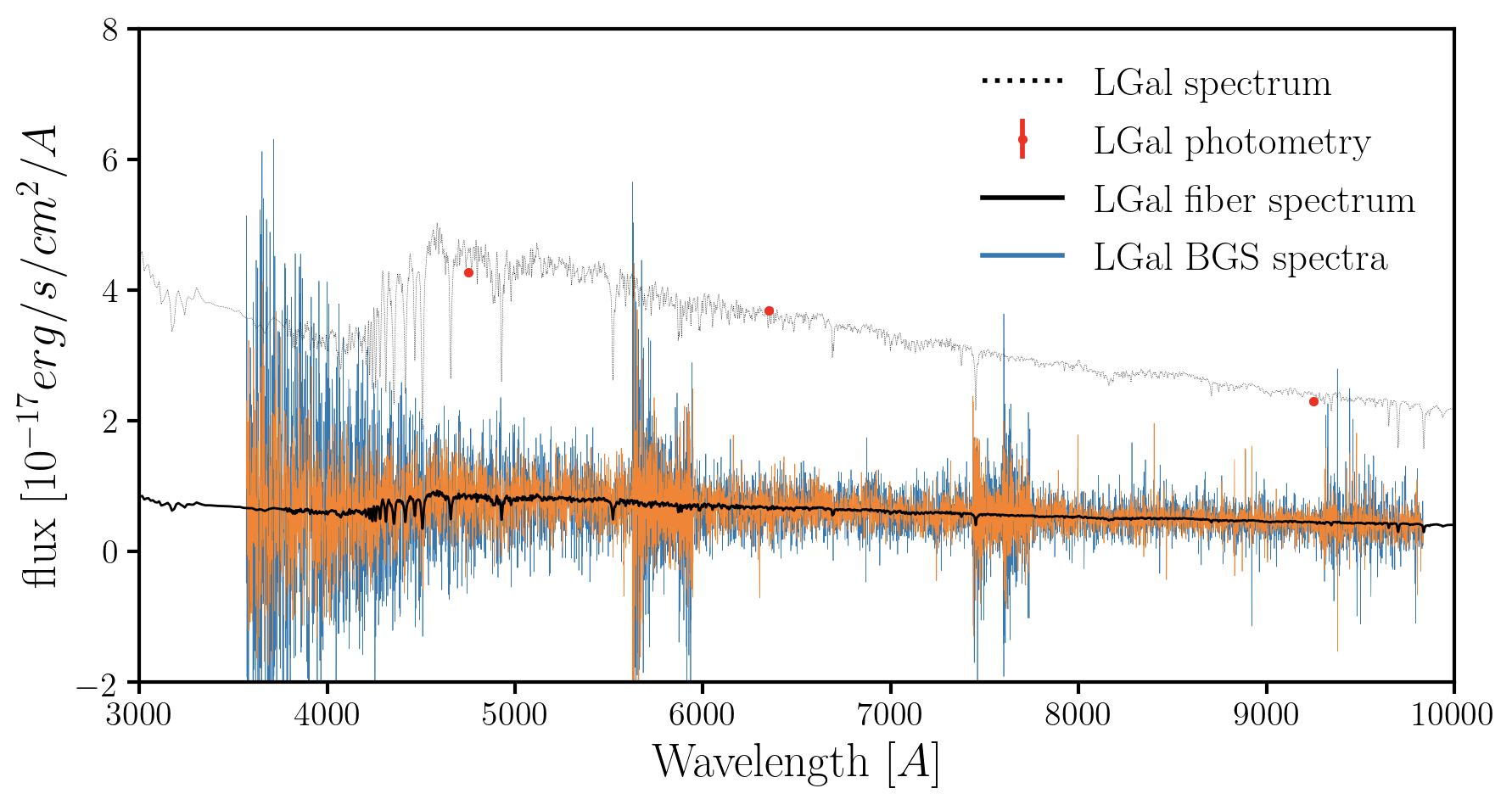
DESI GQP Mock Challenge (MoCha) is currently underway to determine the PROVABGS analysis pipeline
w/ Malgorzata Siudek (IFAE Barcelona), James Kwon (UC Berkeley)
MCMC using speculator, a PCA neural network SPS emulator
percent-level accuracy and >1000x faster
Alsing...CH+(in prep)


galaxy formation models are computationally expensive
possible to make galaxy evolution into an inference problem with simulation-based inference
*also known as "likelihood-free" inference
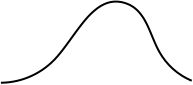
x
θ
consider p(x,θ) for 1D data and 1D parameter
*probably an ideal situation
likelihood p(x|θ)
x
θ
*probably an ideal situation

xobs
posterior p(θ|xobs)
consider p(x,θ) for 1D data and 1D parameter
x
θ
xobs
naive approximate bayesian computation



wastes a lot of simulations ... there are smarter methods (e.g. ABC-PMC; Hahn+2017a,c,2019b)
x
θ
direct density estimation SBI can estimate posteriors much more efficiently (e.g. using ICA and GMM; Hahn+2019c)


only tip of the SBI iceberg!
Density Estimation LFI (Alsing+2019),
ABC with Conditional Density Estimation (Izbicki+2018),
Sequential Neural Posterior Estimation (Lueckmann+2019),
Bayesian Optimization LFI (Gutmann & Corannder 2016),
Inference Aware Neural Optimization (de Castro & Dorigo 2018)
...

the LFI Taskforce is developing new methods for SBI tailored to astronomy
logo credit: @danielhey
w/ Arin Avsar, Tess Werhane, James Zhu, Vanessa Boehm, Francois Lanusse, Jia Liu (Berkeley)
Virginia Ajani (CEA), Will Coulton (Cambridge), Chieh-An Lin (Edinburgh), Nesar Ramachandra (ANL)
empirical models are cheap and easy to interpret:
e.g. constraining SF variability timescale from SHMR (Hahn+2019c)
DESI Bright Galaxy Survey (PROVABGS) --- 10 million galaxies
hydro sims and SAMs are expensive and difficult to interpret
...plenty of room for improvement (Hahn+2019a)
e.g. tighter constraints on tduty, tquench (Hahn+2017c), assembly bias, hierarchical Bayesian modeling
SBI methods will enable direct inference from galaxy surveys
credit: desi.lbl.gov
IQ collaboratory, ABC, DELFI