Graphics Programming Virtual Meetup


Discord
Tiny Renderer
Lesson 6b
Normal Mapping in detail
Tutorial link:
https://github.com/ssloy/tinyrenderer/wiki/Lesson-6bis-tangent-space-normal-mapping
My Code:
https://github.com/cdgiessen/TinyRenderer
What is a normal map?
- Texture containing surface directions
- The RGB color channels represent XYZ vector values
- How those RGB values are interpreted depends on the 'space' of the normal map
- Some 'spaces': Object, Darboux

Object Space
- The RGB values are relative to the center of the object
- A (0,1,0) value would mean the normal points up
- A (1,0,0) value means the normal points in the +X axis
- Can't deform or scale the mesh because the normals wont be altered appropriately
Darboux space (aka Tangent Space)
- The RGB values are local to the surface
- (0,1,0) means point up relative to the interpolated surface normal
- Deformation is a-okay, the normals are always relative to whatever the deformation uses
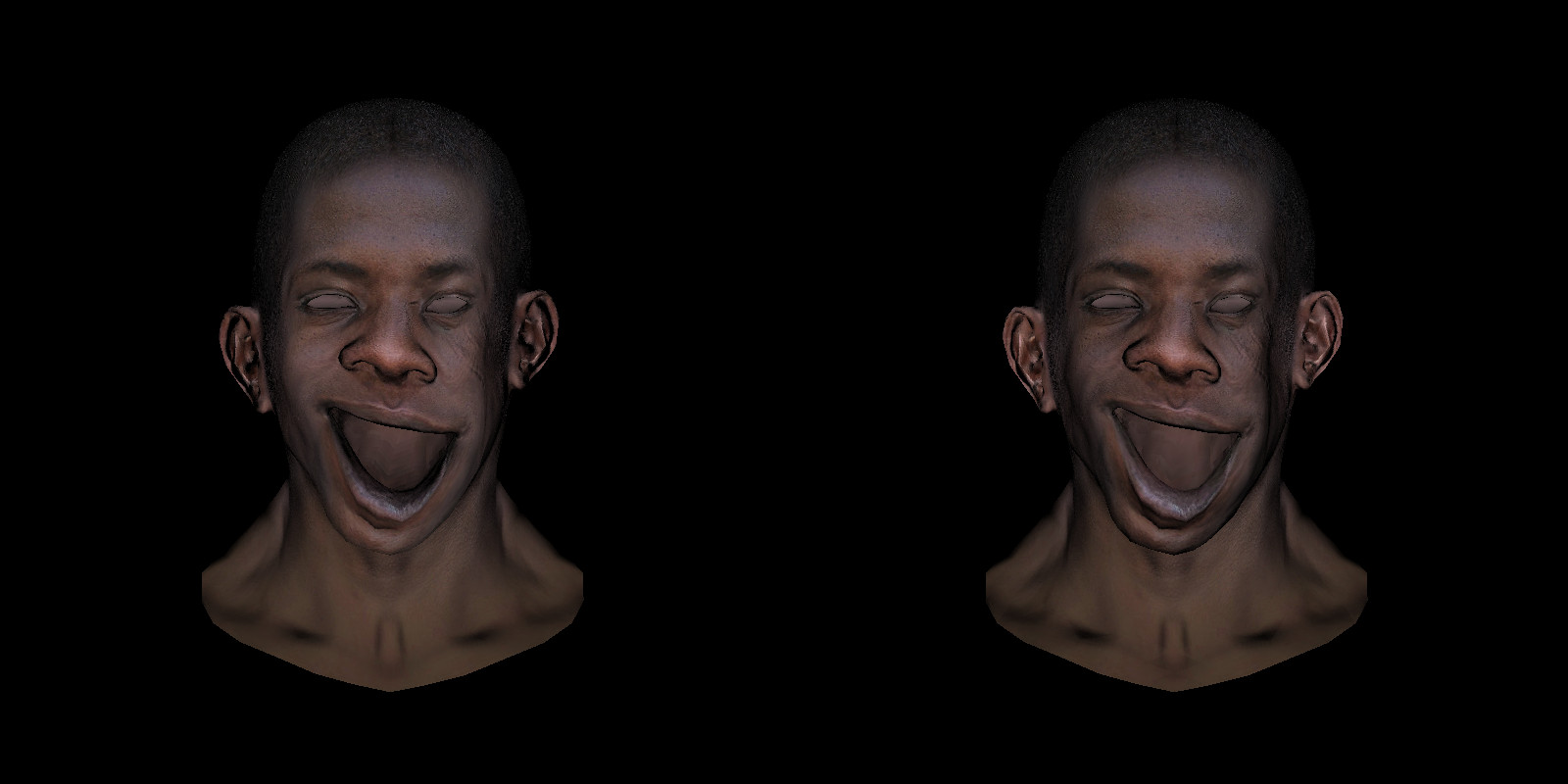
Example deformation

Another example
Note that arms & legs are mirrored
Lets see how we can implement tangent space

Reference 'iso-lines' of our UV space
Lets look at how Phong Shading works
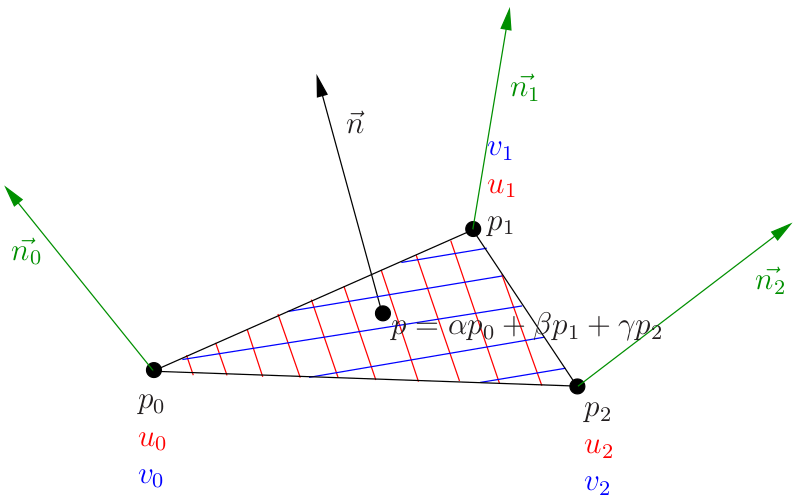
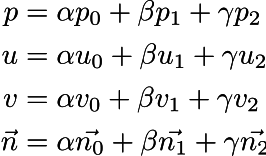
All values of a point are the interpolation between the 3 outer points & their barycentric coordinates
Note that the blue & red lines are all straight, they are the 'axis' in our Darboux frame, eg, the U, V axes
X and Y map to the U and V axis, while Z is the 'up' direction orthogonal to the plane.
That is why Tangent space normal maps appear blue. Most of the time they point 'up', and the Z axis is in the B channel (blue)
Goal: Construct 3 vectors for our tangent basis at each pixel we draw
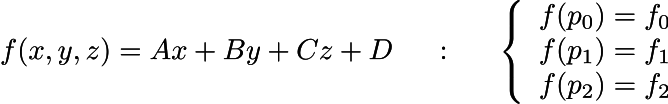
Imagine a linear function f that for each point (x,y,z) gives a real number f(x,y,z) = Ax + By + Cz + D.
We do not know A, B, C and D, however we do know three values of the function at three different points of the space (p0, p1, p2):
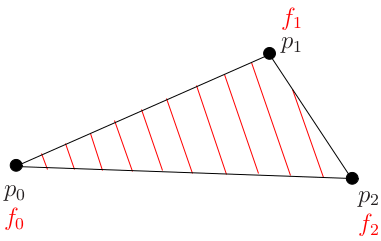
Image f as a 'height map' of an inclined plane.
Fix all three points to this plane and so we know the values at those points on the plane.
Red lines inside the triangle show the iso-heights f0, f0 + 1 meter, f0 + 2 meters and so on.
Recall that the steepest ascent direction for a function is its gradient
For a linear function f(x,y,z) = Ax + By + Cz + D,
its gradient is a constant vector (A, B, C).
Remember that we don't know (A, B, C) but do know f0, f1, and f2.
We have three points p0, p1, p2 and three values f0, f1, f2. We need to find the vector of the steepest ascent (A,B,C).
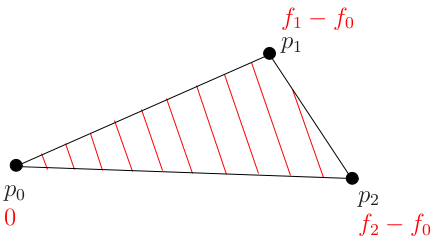
Let us consider another function defined as g(p) = f(p) - f(p0):
The steepest ascent direction for f and g is the same.
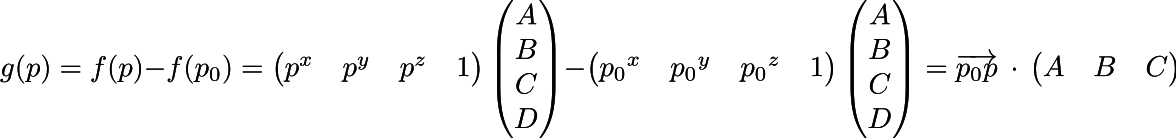
Rewrite g
function g is a dot product between vector (p-p0) and (ABC)
Recall that if we go from point p0 to point p2, then the function g will go from zero to f2-f0.
The dot product between vectors (p2-p0) and (ABC) is equal to f2-f0, and the same applies for (p1-p0)
Therefore, vector ABC is orthogonal to normal n and respecting two constraints on dot products
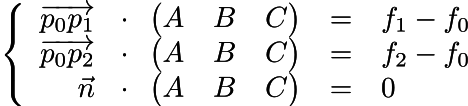
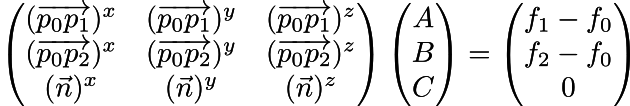
Rewrite in matrix form
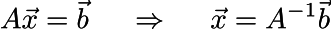
This yields an easy to solve linear matrix equation of the form Ax = b:
The Darboux basis (tangent space) is a triplet of vectors (i,j,n) where n is the original normal vector, and i, j can be computed with
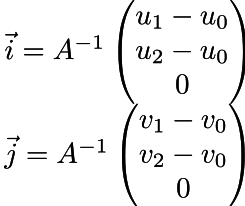
Now for the code which implements it
mat<3,3> A;
A[0] = ndc_tri.col(1) - ndc_tri.col(0);
A[1] = ndc_tri.col(2) - ndc_tri.col(0);
A[2] = bn;
mat<3,3> A_I = A.invert();
vec3f i = A_I * vec3f(uv[0][1] - uv[0][0], uv[0][2] - uv[0][0], 0);
vec3f j = A_I * vec3f(uv[1][1] - uv[1][0], uv[1][2] - uv[1][0], 0);
Apply the change of basis, and voila!