Projective Geometric Algebra:
A Swiss army knife for doing
Cayley-Klein geometry
Charles Gunn
Sept. 18, 2019 at ICERM, Providence
Full-featured slides available at: https://slides.com/charlesgunn3/icerm2019.
Check for updates incorporating new ideas inspired by giving the talk.
This first slide will indicate whether update has occurred.
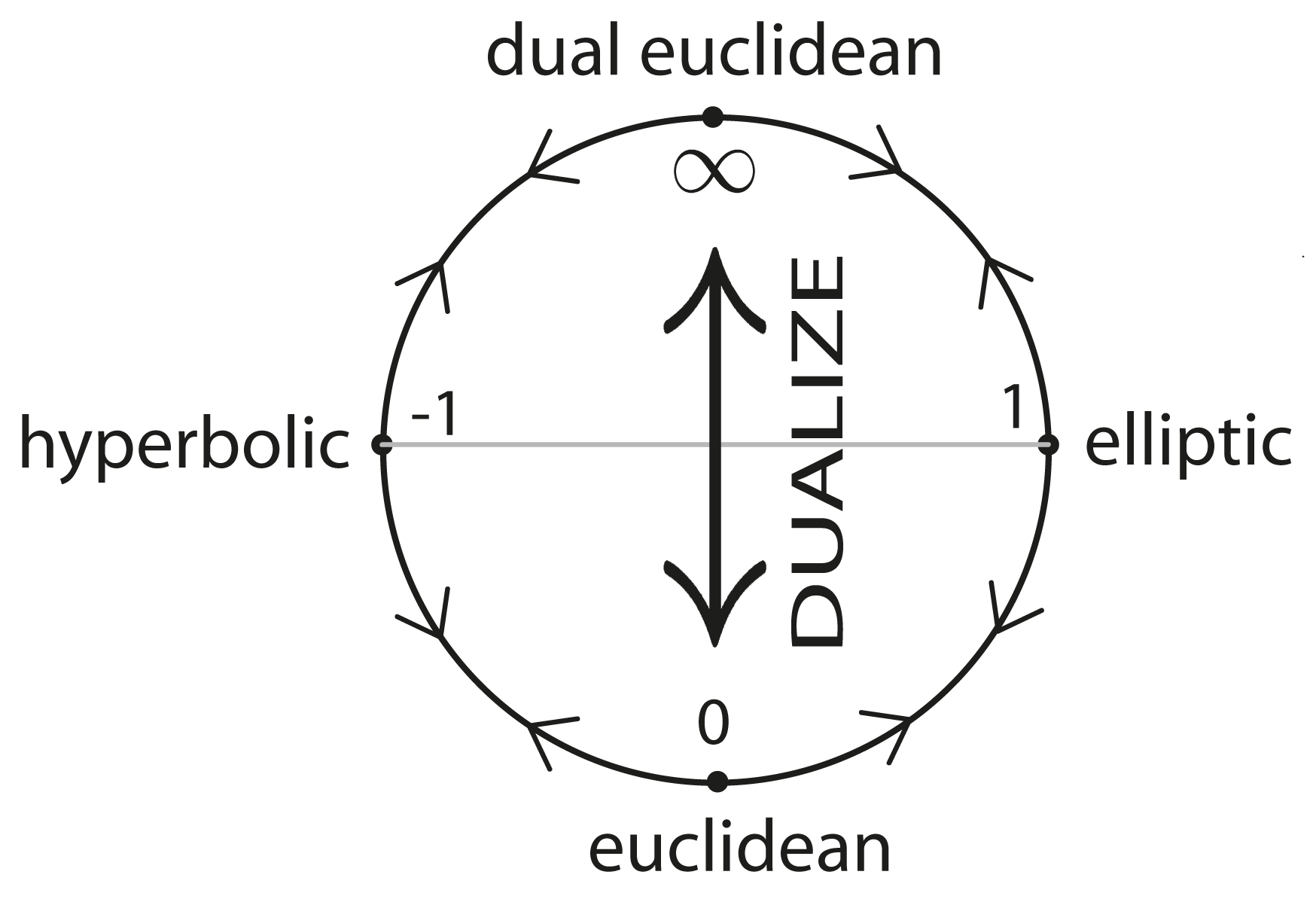
What is Cayley-Klein geometry?


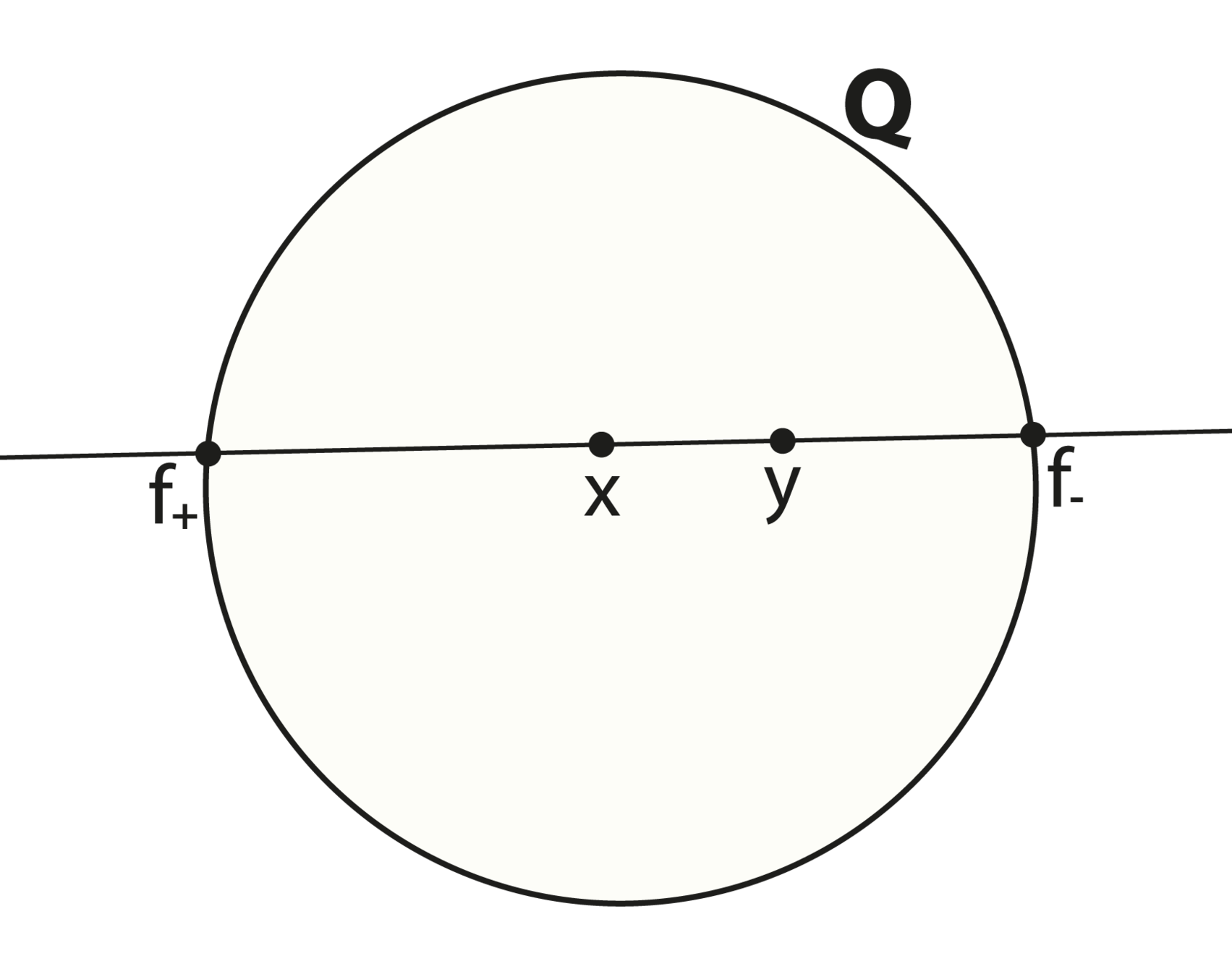
What is Cayley-Klein geometry?


SIGNATURE of Quadratic Form
Example: \((++-0) = (2,1,1)\)
\(~e_0\cdot e_0 = e_1\cdot e_1 = +1,~e_2\cdot e_2=-1,~e_3\cdot e_3=0,\)\(~~e_i\cdot e_j = 0 ~\text{for}~i\neq j\)
What is Cayley-Klein geometry?


| Signature of Q | Space | Symbol | |
|---|---|---|---|
| +1 | elliptic | ||
| -1 | hyperbolic | ||
| 0 | euclidean |
\((n+1,0,0)\)
$$\bf{E}^n$$
$$\bf{H}^n$$
$$\bf{Ell}^n,\bf{S}^n$$
\((n,1,0)\)
\("(n,0,1)"\)
\(\kappa\)
The Sudanese Moebius band in \(S^3\) discovered by Sue Goodman and Dan Asimov, visualized in UNC-CH Graphics Lab, 1979.
3D Examples

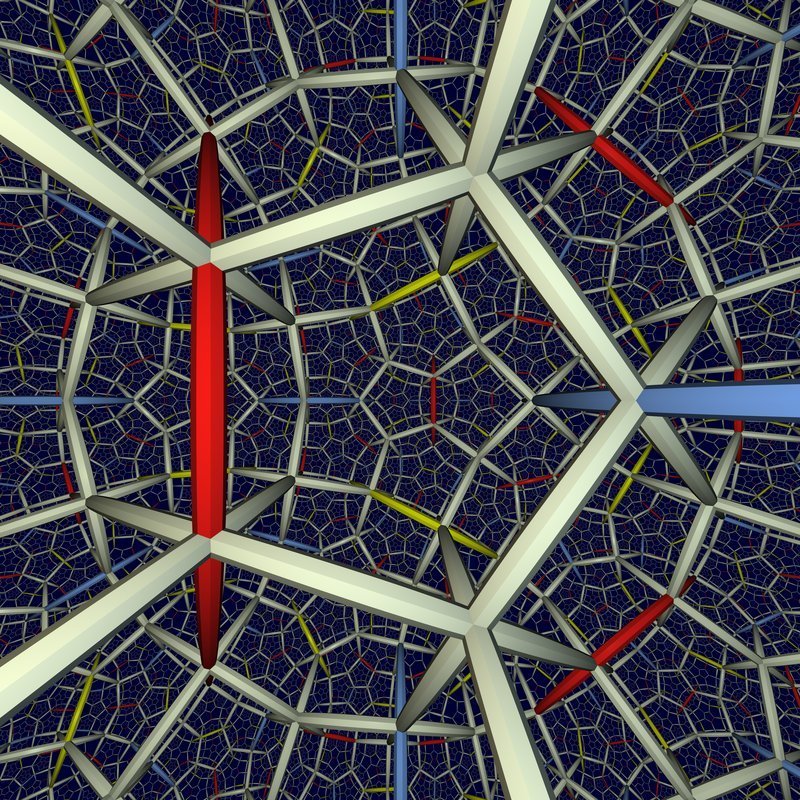
Tessellation of \(H^3\) with regular right-angled dodecahedra (from "Not Knot", Geometry Center, 1993).
3D Examples
The 120-cell, a tessellation of the 3-sphere \(\bf{S}^3\)
(PORTAL VR, TU-Berlin, 18.09.09)

3D Examples



| Name | elliptic | euclidean | hyperbolic |
|---|---|---|---|
| signature | (3,0,0) | "(2,0,1)" | (2,1,0) |
| null points |
\(x^2+y^2+z^2\)=0
\(z^2\)=0
\(x^2+y^2-z^2\)=0
Cayley-Klein geometries for n = 2
| Name | elliptic | euclidean | hyperbolic |
|---|---|---|---|
| signature | (3,0,0) | "(2,0,1)" | (2,1,0) |
| null points | |||
| null lines* |
\(x^2+y^2+z^2\)=0
\(z^2\)=0
\(x^2+y^2-z^2\)=0
\(a^2+b^2+c^2\)=0
\(a^2+b^2-c^2\)=0
\(a^2+b^2\)=0
*The line \(ax+by+cz=0\) has line coordinates \((a,b,c)\).



Example Cayley-Klein geometries for n = 2
Question
What is the best way
to do Cayley-Klein geometry
on the computer?


1993
2019

Projective
points
Projective
matrices
Vector + linear algebra
Projective
points
Projective
matrices
Vector + linear algebra
But it's 2019 now. Can we do better?

Coordinate-free
Uniform rep'n for points, lines, and planes
Cayley-Klein programmer's wish list

Single, uniform rep'n for isometries
Parallel-safe meet and join operators
Compact expressions for classical geometric results
Physics-ready
Metric-neutral
Backwards compatible

Partial solutions: Quaternions (1843)
A 4D algebra generated by units \(\{1,\mathbf{i},\mathbf{j},\mathbf{k}\}\) satisfying:
$$1^2=1,~~\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=-1$$ $$\mathbf{i}\mathbf{j}=-\mathbf{j}\mathbf{i},\text{...}$$
Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
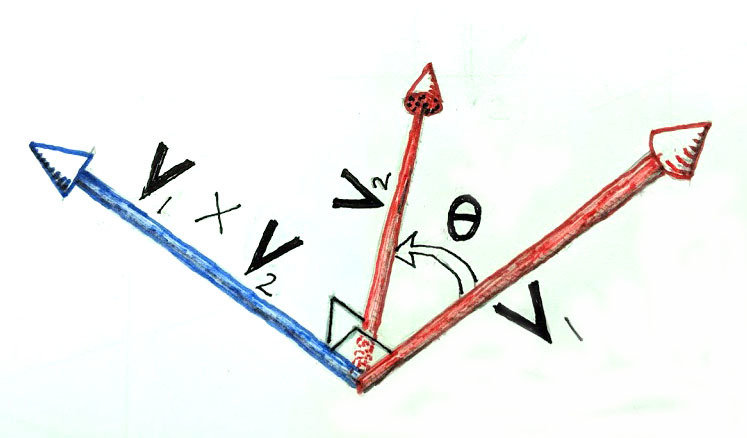
I. Geometric product:
$$\mathbf{v}_1\mathbf{v}_2 = -\mathbf{v}_1 \cdot \mathbf{v}_2 + \mathbf{v}_1 \times \mathbf{v}_2$$
cross product
inner product
Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
II. Rotations via sandwiches:
1. For \(\mathbf{g} \in \mathbb{U}\), there exists \(\mathbf{x} \in \mathbb{IH}\) so that
$$\mathbf{g} = \cos(t)+\sin(t)\mathbf{x} = e^{t\mathbf{x}}$$
2. For any \(\mathbf{v} \in \mathbb{IH}~~ (\cong \mathbb{R}^3)\), the "sandwich" $$ \mathbf{g}\mathbf{v}\overline\mathbf{g}$$ rotates \(\mathbf{v}\) around the axis \(\mathbf{x}\) by an angle \(2t\).
3. Comparison to matrices.
Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
Advantages
I. Geometric product
II. Rotations as sandwiches
Disadvantages
I. Only applies to points/vectors
II. Special case \(\mathbb{R}^3\)
Quaternions
Partial solutions: Grassmann algebra

Hermann Grassmann (1809-1877)
Ausdehnungslehre (1844)
Grassmann algebra
The wedge (\(\wedge\)) product in \(\mathbb{R}P^2\) and \(\mathbb{R}P^{2\large*}\)
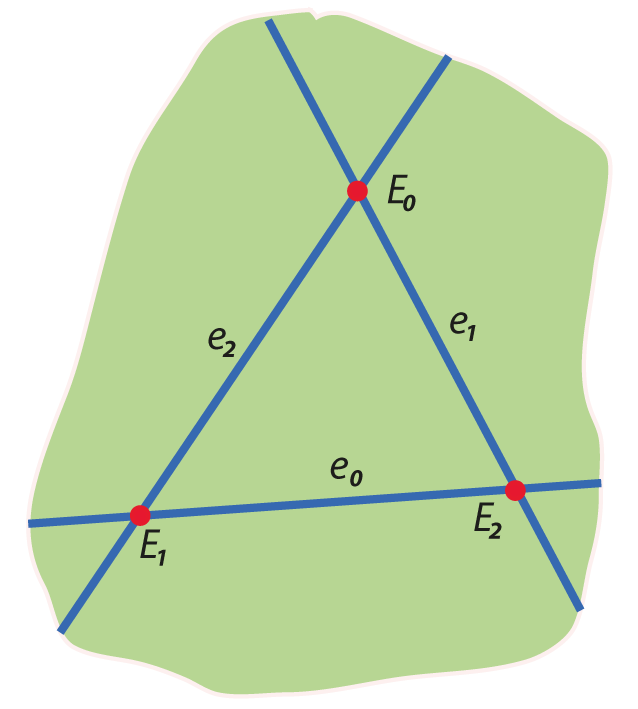
Standard projective
\(\mathbf{x}\wedge\mathbf{y}\) is join
yields \(\bigwedge\mathbb{R}P^2\)
Dual projective
\(\mathbf{x}\wedge\mathbf{y}\) is meet
yields \(\bigwedge\mathbb{R}P^{2\large*}\)
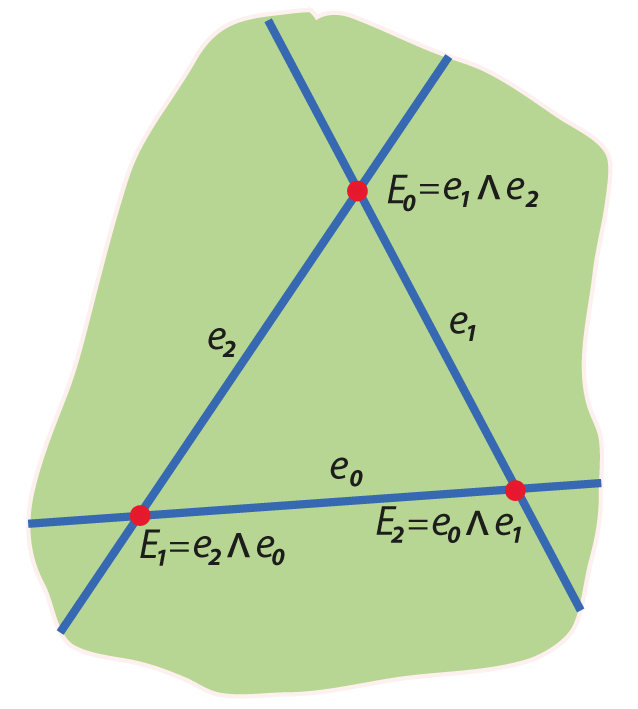
Grassmann algebra

| Grade | Sym | Generators | Dim. | Type |
|---|---|---|---|---|
| 0 | 1 | 1 | Scalar | |
| 1 | 3 | Line | ||
| 2 | 3 | Point | ||
| 3 | 1 | Pseudoscalar |
\(\bigwedge^3\)
\(\bigwedge^2\)
\(\bigwedge^1\)
\(\bigwedge^0\)
\(\{\mathbf{e}_0,\mathbf{e}_1,\mathbf{e}_2\}\)
\(\{\mathbf{E}_i = \mathbf{e}_j\wedge\mathbf{e}_k\}\)
\(\mathbf{I}=\mathbf{e}_0\wedge\mathbf{e}_1\wedge\mathbf{e}_2\)
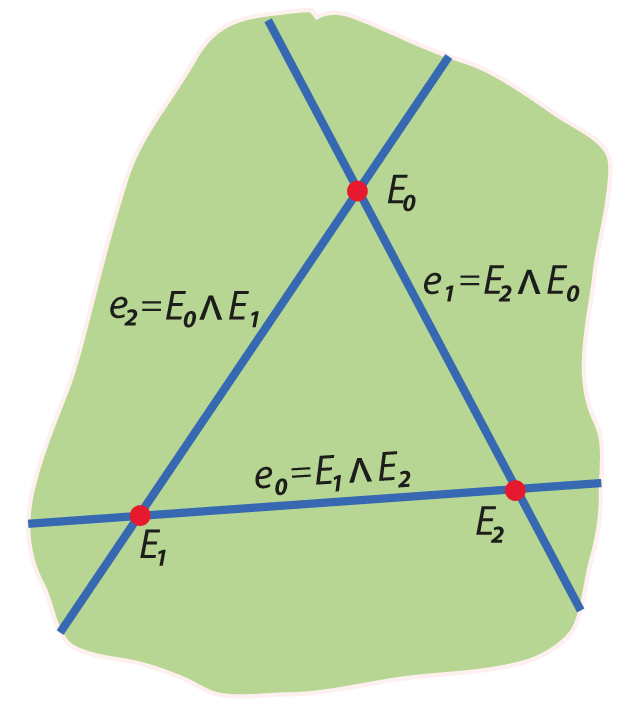
We will be using \(\bigwedge\mathbb{R}P^{n\large{*}}\) for the rest of the talk.
The dual projective Grassmann algebra \(\bigwedge\mathbb{R}P^{2\large*}\)
Grassmann algebra
Properties of \(\wedge\)
1. Antisymmetric: For 1-vectors \(\mathbf{x}, \mathbf{y}\):$$\mathbf{x}\wedge\mathbf{y}=-\mathbf{y}\wedge\mathbf{x}$$$$\mathbf{x}\wedge\mathbf{x}=0$$
2. Subspace lattice: For linearly independent subspaces \(\mathbf{x}\in\bigwedge^k,\mathbf{y}\in\bigwedge^{m}\), \(\mathbf{x}\wedge\mathbf{y}\in\bigwedge^{k+m}\) is the subspace spanned by \(\mathbf{x}\) and \(\mathbf{y}\) otherwise it's zero.

Note: The regressive (join) product \(\large\vee\) is also available.
(Then it's called a Grassmann-Cayley algebra.)
The wedge (\(\wedge\)) product in \(\mathbb{R}P^2\)
Grassmann algebra
Note: spanning subspace means different things in standard and dual setting. In 3D:
Standard: a line is the subspace spanned by two points.
Dual: a line is the subspace spanned by two planes.
Point range
Spear
Plane pencil
Axis
Grassmann algebra
Advantages
1. Points, lines, and planes are equal citizens.
2. "Parallel-safe" meet and join operators since projective.
Disadvantages
1. Only incidence (projective), no metric.
Grassmann algebra
Clifford's geometric algebra

William Kingdon Clifford (1845-1879)
"Applications of Grassmann's extensive algebra" (1878):
His stated aim: to combine quaternions with Grassmann algebra.
Clifford's geometric algebra
Geometric product extends the wedge product and is defined for two 1-vectors as: $$\large{\mathbf{x}\mathbf{y} := \mathbf{x}\large{\cdot}\mathbf{y} + \mathbf{x}\wedge\mathbf{y}}$$
where \(\cdot\) is the inner product induced by \(\mathbf{Q}\).
0-vector
2-vector
This product can be extended to the whole Grassmann algebra to produce the geometric algebra \(\mathbf{P}(\mathbb{R}^*_{p,n,z})\).
measures sameness
measures difference
Since the two terms measure different aspects, the sum is (usually) non-zero.
Projective geometric algebra
We call an algebra constructed in this way a projective geometric algebra (PGA).
We are interested in \(\mathbf{P}(\mathbb{R}^*_{3,0,0}) \), \(\mathbf{P}(\mathbb{R}^*_{2,1,0}) \), \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \).
We sometimes write \(\mathbf{P}(\mathbb{R}^*_\kappa)\) and leave the metric open.
We can choose a fundamental triangle so that:
$$\mathbf{e}_0^2 = \kappa, \mathbf{e}_1^2=\mathbf{e}_2^2=1$$ $$(\kappa\in\{-1,0,1\})$$
$$\mathbf{E}_k:=\mathbf{e}_i\mathbf{e}_j = \mathbf{e}_i\wedge\mathbf{e}_j = -\mathbf{e}_j\mathbf{e}_i$$
$$\mathbf{I}:=\mathbf{e}_0\mathbf{e}_1\mathbf{e}_2$$
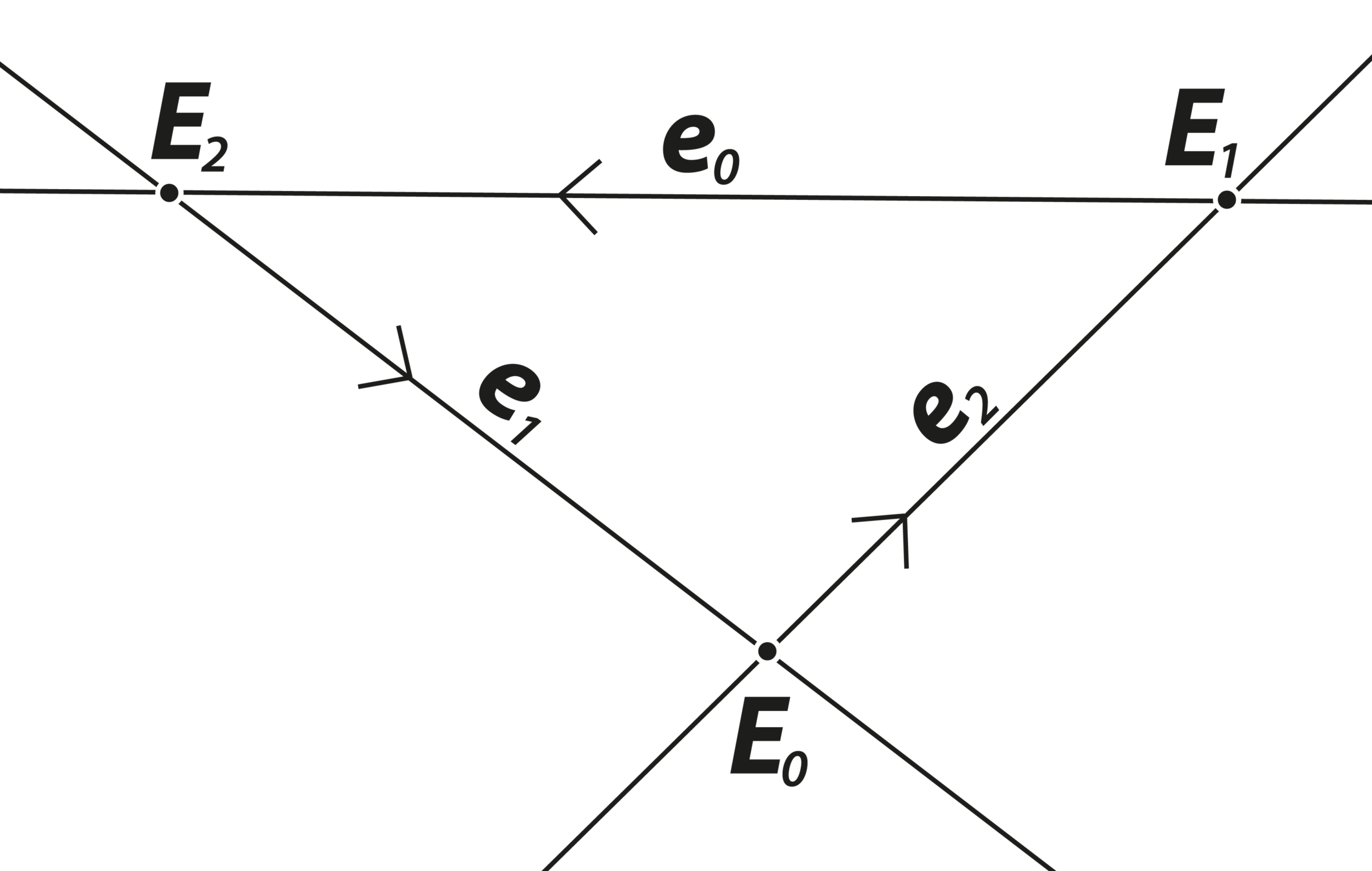
2D PGA
Example: Two lines, let \(e_0^2=\kappa\) $$\mathbf{a} = a_0 e_0+a_1 e_1 + a_2 e_2$$ $$ \mathbf{b} = b_0 e_0 + b_1e_1+b_2e_2$$ $$\mathbf{ab}=(a_0b_0e_0^2+a_1b_1e_1^2+a_2b_2e_2^2)$$ $$+(a_0b_1 - a_1b_0)e_0e_1 + (a_1b_2-a_2b_1)e_1e_2 + (a_0b_2-a_2b_0)e_0e_2$$ $$ = (a_0b_0\kappa+a_1b_1+a_2b_2)$$ $$+(a_1b_2-a_2b_1)E_0+(a_2b_0-a_0b_2)E_1+(a_0b_1-a_1b_0)E_2$$ $$= \mathbf{a}\cdot \mathbf{b} + \mathbf{a}\wedge \mathbf{b}$$
Looks like cross product but is the point incident to both lines.
2D PGA
Example: \(\kappa=1\) and \(c=\frac1{\sqrt{2}}\) and $$\mathbf{a} = e_0,~~~\mathbf{b} = ce_0+ ce_1$$
Then \(\mathbf{a}^2=\mathbf{b}^2=1\).
\(\mathbf{a}\) is the equator great circle \(z=0\) and \(\mathbf{b}\) is tilted up from it an angle of \(45^\circ\). $$\mathbf{ab}= c+E_2$$ Check: \(\cos^{-1}(c) = 45^\circ\) and \(\mathbf{E}_2\) is the common point.
2D Euclidean PGA
We can now explain why \(P(\mathbb{R}^*_{2,0,1})\) is the right choice for the euclidean plane.
The inner product of two lines is $$\mathbf{a\cdot b}= (a_0b_0\kappa+a_1b_1+a_2b_2)$$
For a euclidean line changing \(a_0\) or \(b_0\) doesn't change the direction of the line. It just moves it parallel to itself. This means \(e_0^2=0\).

Clifford's geometric algebra
0-vector
2-vector
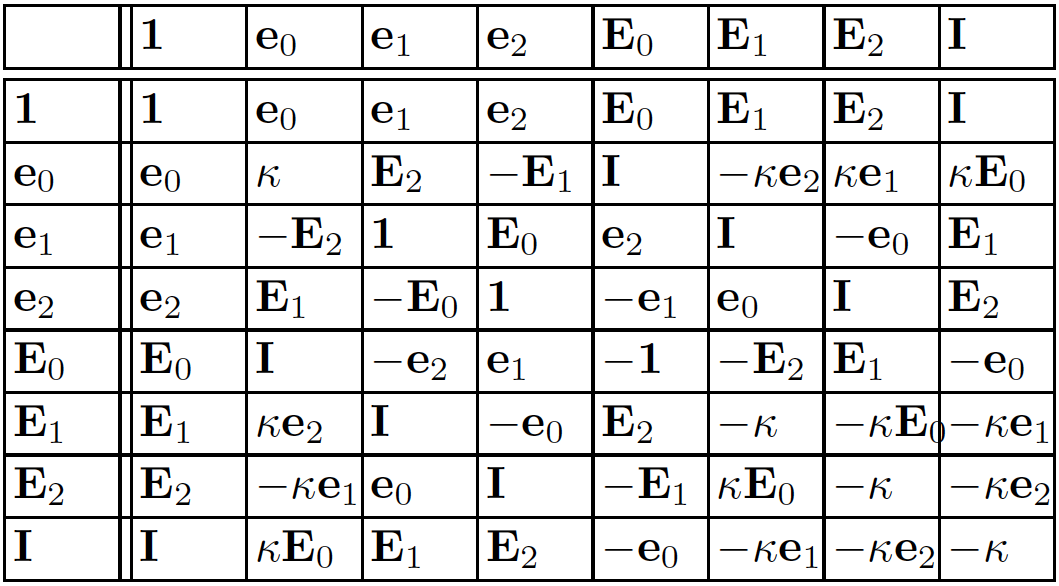
Multiplication table for 2D PGA. \(\kappa \in \{-1,0,1\}\)
2D PGA Preliminaries
1. We can normalize a proper line \(\mathbf{m}\) or point \(\mathbf{P}\) so that:$$\mathbf{m}^2 = 1,~~~\mathbf{P}^2 = -\kappa$$
1a. Elements such that \(\mathbf{x}^2=0\) are called ideal.
1b. Formulas given below often assume normalized arguments.
PGA: 2-way products
2. Multiplication with \(\mathbf{I}\): For any k-vector \(\mathbf{x}\), \(\mathbf{x}^\perp := \mathbf{x}\mathbf{I}\) is the orthogonal complement of \(\mathbf{x}\).
Example: \(\mathbf{e}_0 \mathbf{I} = \kappa\mathbf{e}_1\mathbf{e}_2\). The only thing left in \(\mathbf{I}\) is what isn't in \(\mathbf{X}\).
2a. In the euclidean case, \(\mathbf{I}^2=0\).
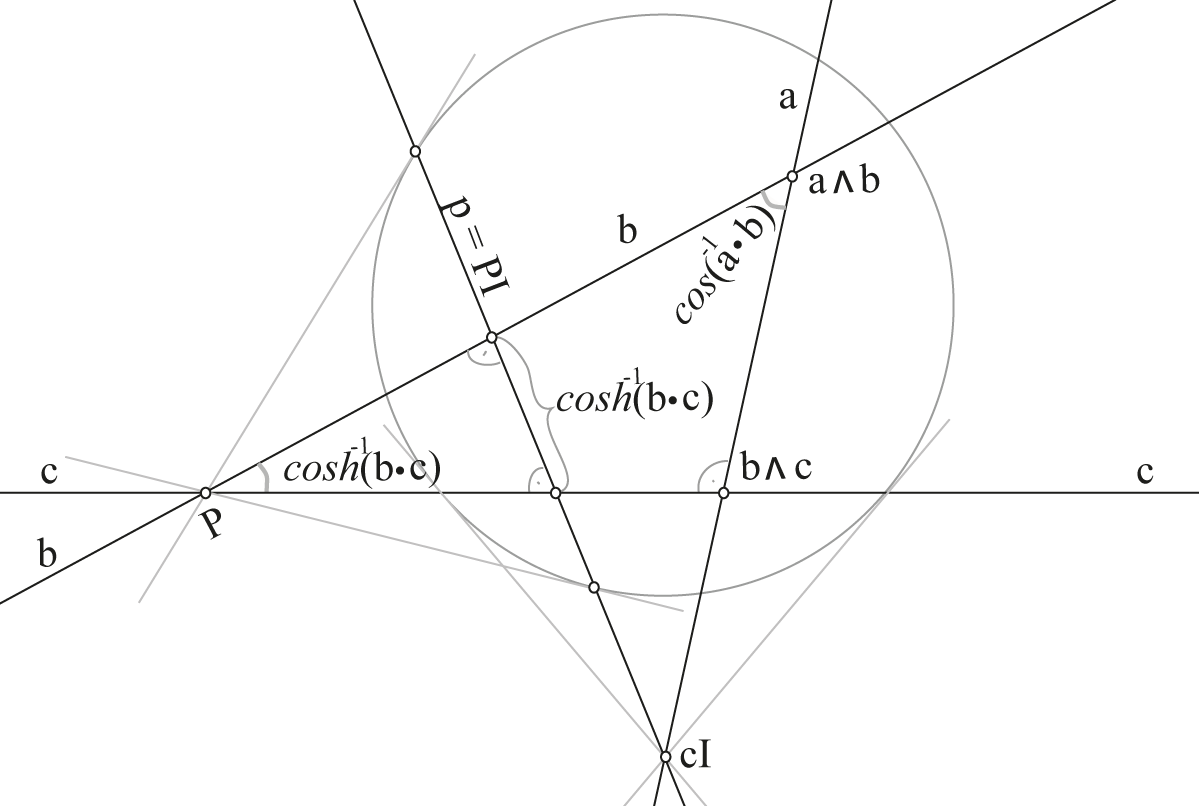
PGA: 2-way products
3. Product of two proper lines \(\mathbf{a},\mathbf{b}\) that meet at a proper point \(\mathbf{P}\):
$$\mathbf{a}\mathbf{b} = \cos(t) + \sin{(t)}\mathbf{P}$$
where \(t\) is the angle between the lines (arbitrary \(\kappa\)).

PGA: 2-way products
3a. Product of two proper lines \(\mathbf{a},\mathbf{b}\) \(\kappa = -1\), \(\mathbf{P}\) is hyper-ideal point. Then
$$\mathbf{a}\mathbf{b} = cosh(d) + \sinh(d)\mathbf{P}$$
where \(d\) is the hyperbolic distance between the lines.

PGA: 2-way products
4. Product of proper line \(\mathbf{c}\) and proper point \(\mathbf{Q}\):
$$\mathbf{c}\mathbf{Q} = \mathbf{c} \cdot \mathbf{Q} + (\cosh{d)}\mathbf{I}~(=\langle cQ\rangle_1+\langle cQ \rangle_3)$$
The first term is the line through \(\mathbf{Q}\) perpendicular to \(\mathbf{c}\), sometimes written \(\mathbf{a}^\perp_\mathbf{Q}\). \(d\) is the distance from point to line.
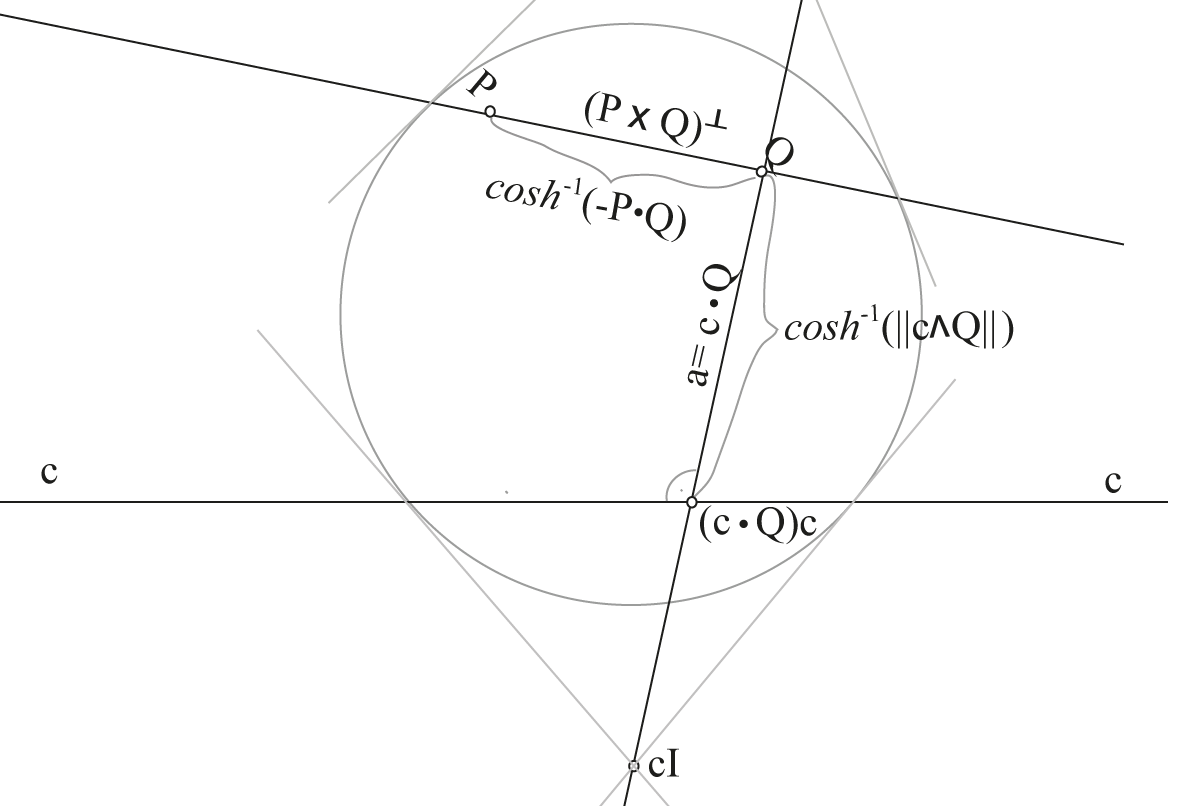
PGA: 2-way products
5. Product of two proper points \(\mathbf{P}, \mathbf{Q}\). Then
$$\mathbf{P}\mathbf{Q}=\cosh(d)+\sinh(d)\mathbf{R}$$
\(d\) is the distance between the two points and \(\mathbf{R}\) is the normalized form of \(\langle \mathbf{P}\mathbf{Q}\rangle_2\), which is the common orthogonal \((\mathbf{P}\vee\mathbf{Q})^\perp\).

Isometries via 3-way products
Reflections
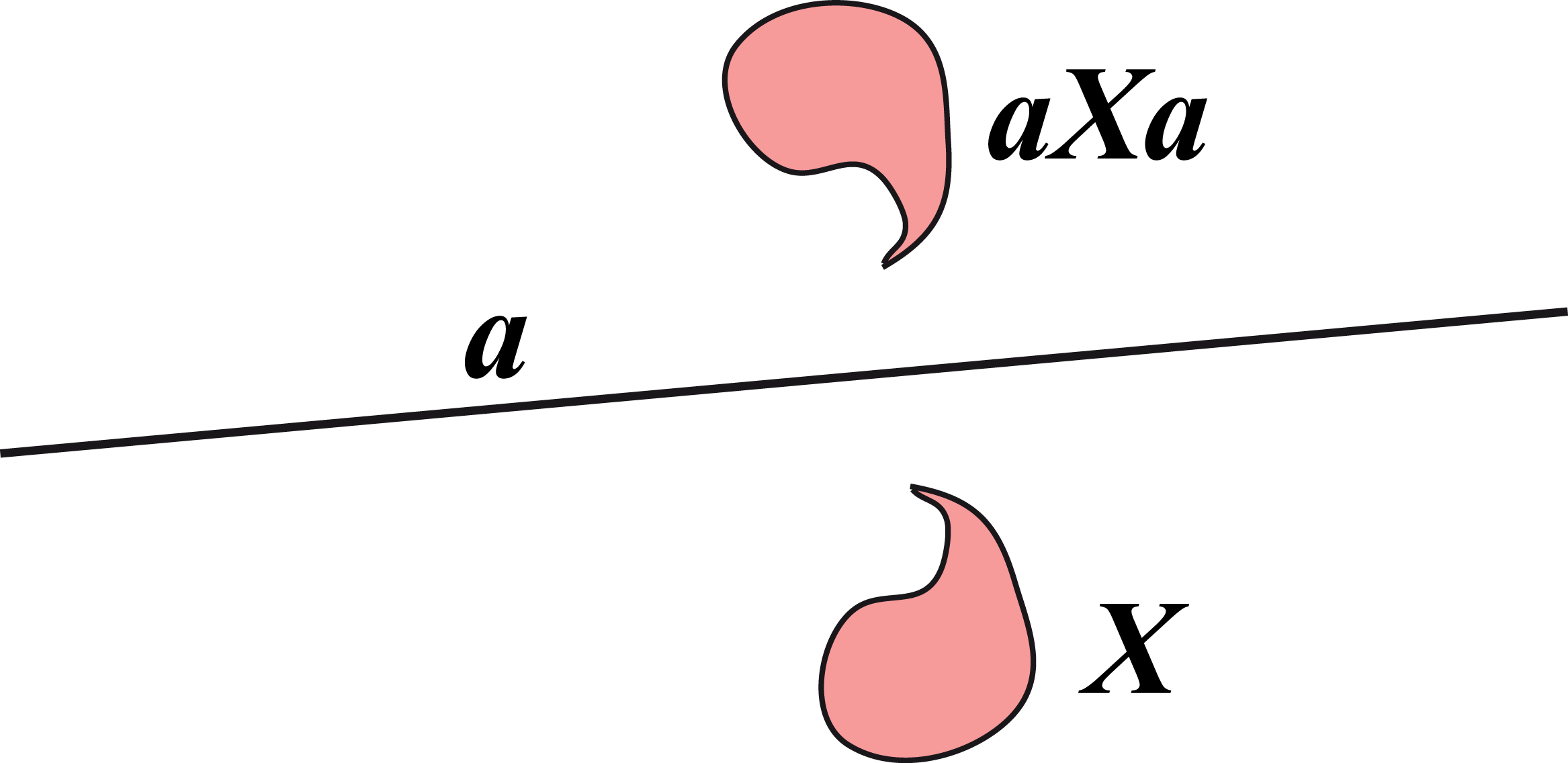
Consider the 3-way product \(\mathbf{X}'=\mathbf{a}\mathbf{X}\mathbf{a}\), where \(\mathbf{a}\) is a proper line and \(\mathbf{X}\) is anything.
Then \(\mathbf{X}'\) is the reflection of \(\mathbf{X}\) in the line \(\mathbf{a}\).
Rotations
A reflection in a second proper line \(\mathbf{b}\) gives \(\mathbf{X}'=\mathbf{b}(\mathbf{a}\mathbf{X}\mathbf{a})\mathbf{b} = (\mathbf{b}\mathbf{a})\mathbf{X}(\mathbf{a}\mathbf{b})\), by associativity. \(\mathbf{r}:=\mathbf{b}\mathbf{a}\) is called a rotor and \(X'=RX\widetilde{R}\) where \(\widetilde{R}\) is reversal operator.
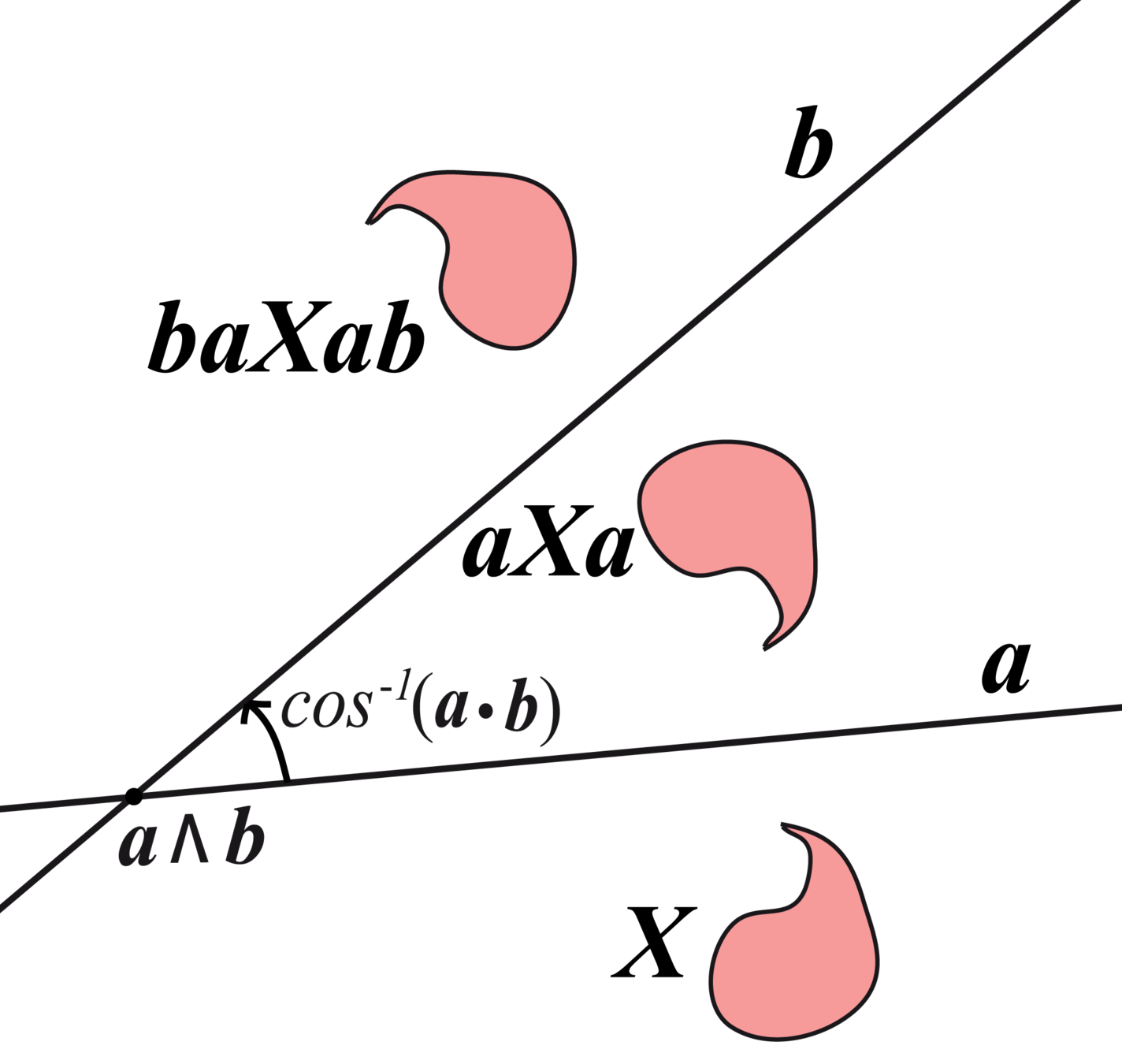
Isometries via 3-way products
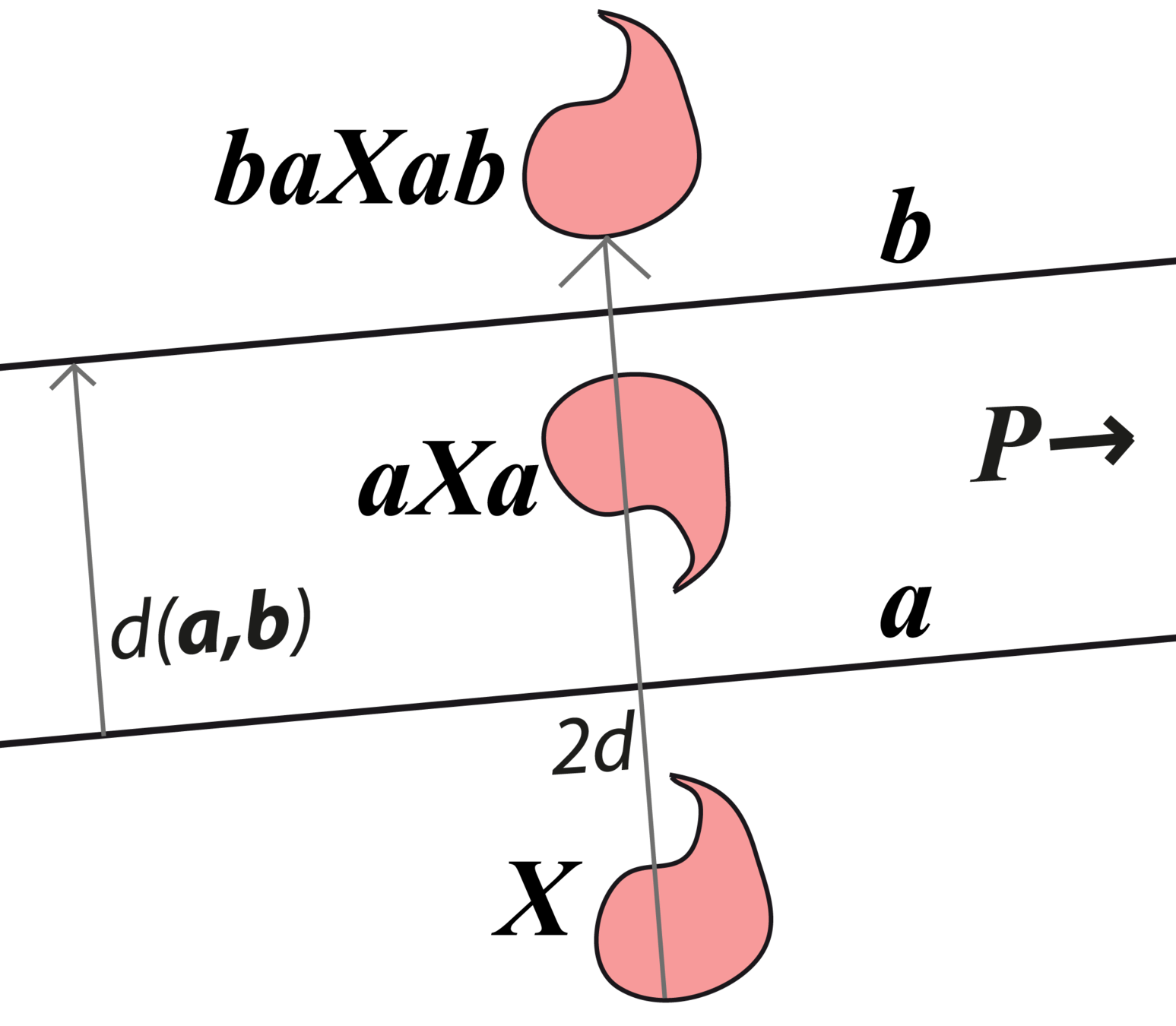
Euclidean translations
If \(\kappa=0\) and \(\mathbf{P}\) is ideal, \(\mathbf{X}'\) is a translation of distance 2d, where d is the distance betwen a and b. Similar results for \(\kappa = -1\).
Isometries via 3-way products
Quaternions in 2D elliptic PGA
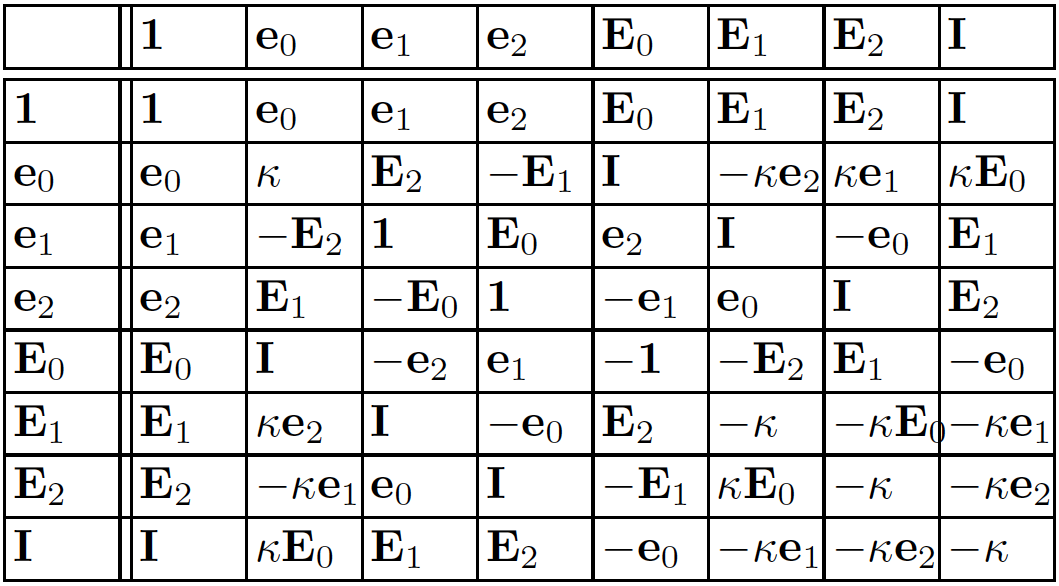
For \(\kappa=1\), the even sub-algebra (shown in red) is isomorphic to \(\mathbb{H}\) under the map $$\{1,\mathbf{E}_0,\mathbf{E}_1,\mathbf{E}_2\}\Leftrightarrow\{1,\mathbf{k},\mathbf{j},\mathbf{i}\}$$
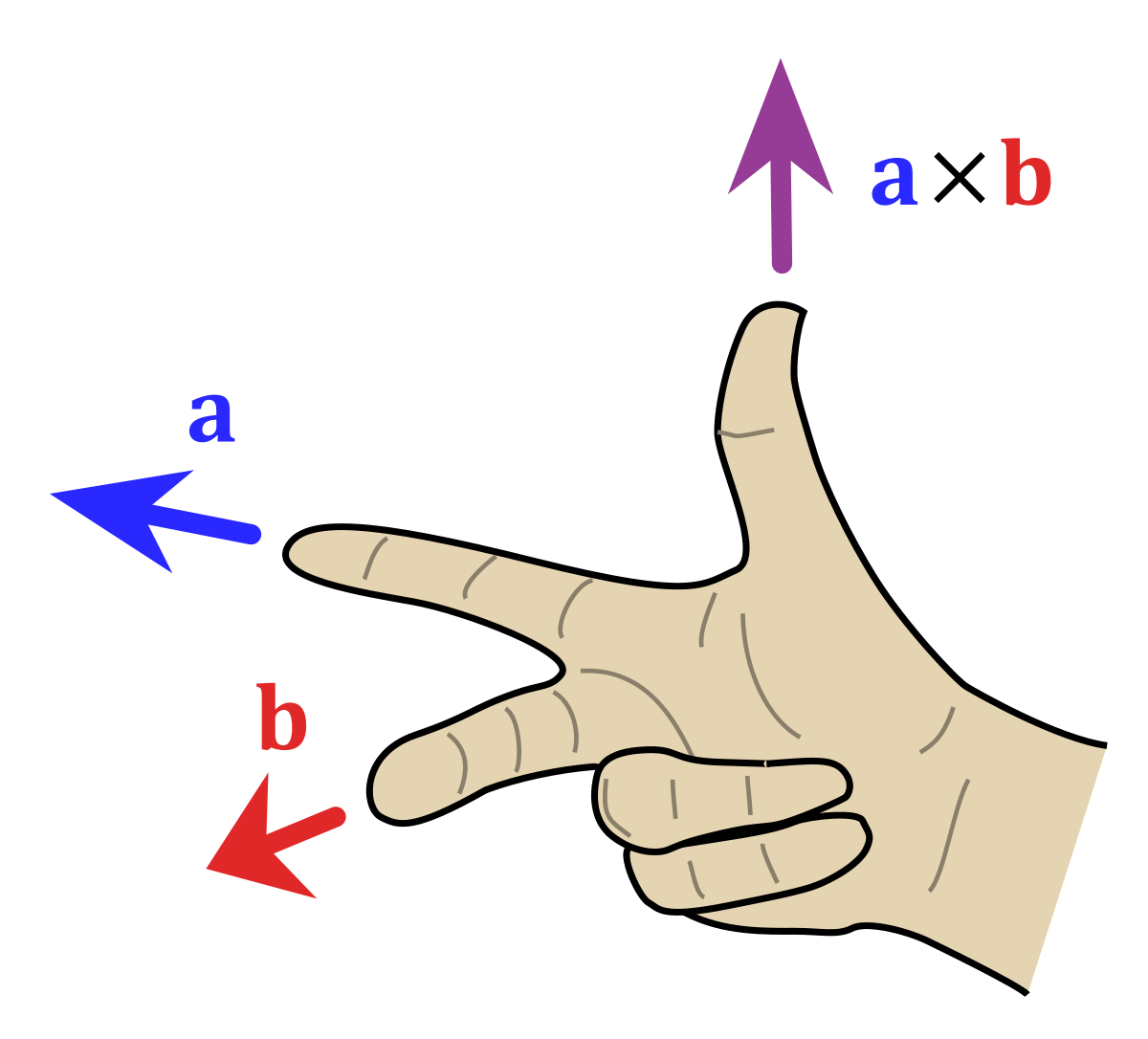
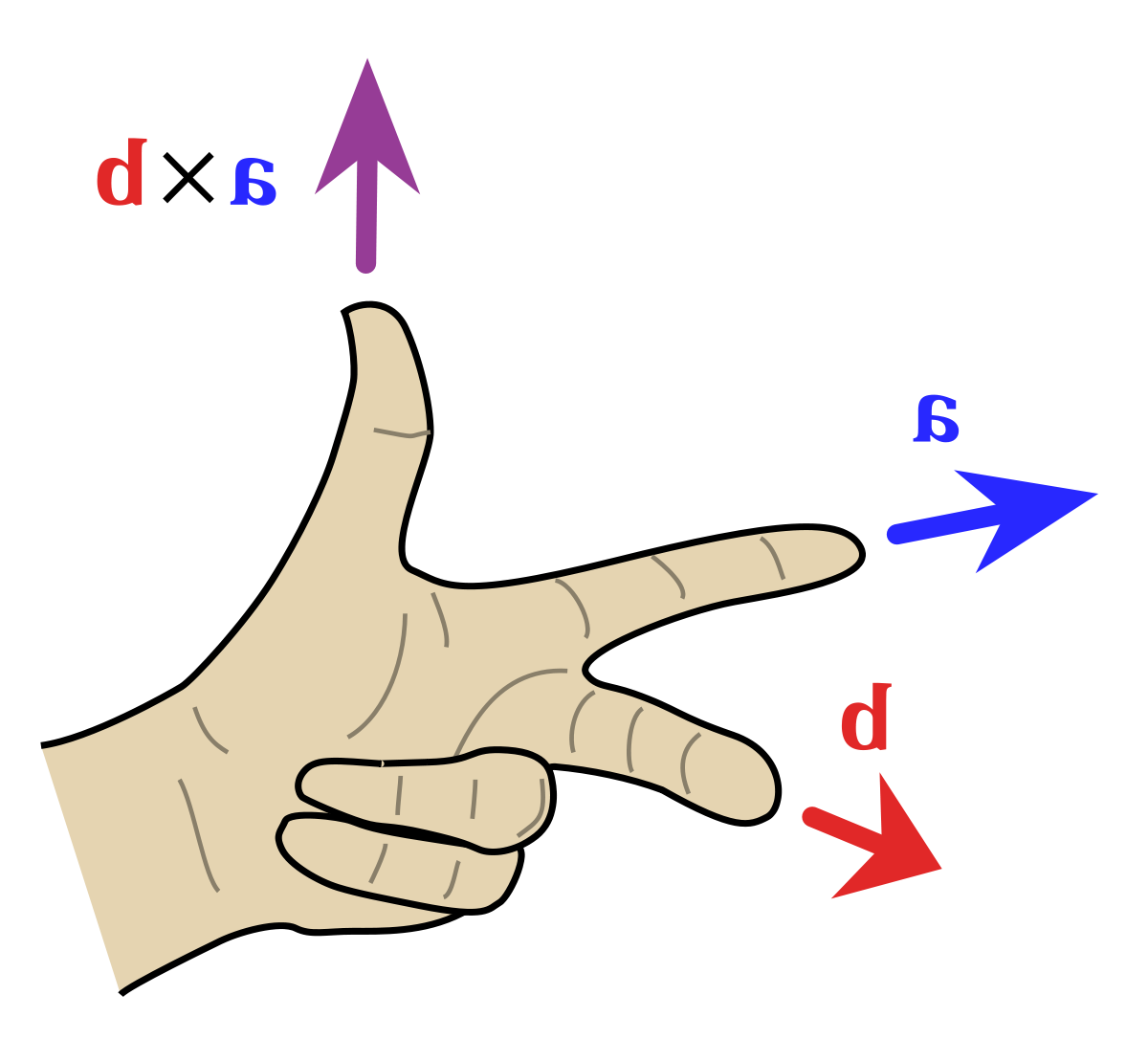
Every rotor can be produced directly by exponentation of a bivector. When \(\mathbf{P}^2=-1\) then
$$\mathbf{r} := \exp(t\mathbf{P}) = \cos(t) + \sin(t)\mathbf{P}$$
\(\mathbf{r}\mathbf{X}\widetilde{\mathbf{r}}\) produces a rotation through angle \(2t\) around \(\mathbf{P}\).
Analogous results hold for \(\mathbf{P}^2=0 \text{ or } 1\) yielding parabolic or hyperbolic isometries.
The ideal norm
\(\mathbf{P}^2 = 0\): how to normalize \(\mathbf{P}\) so \(e^{dP}\) is a translation of 2d? Time permitting ...
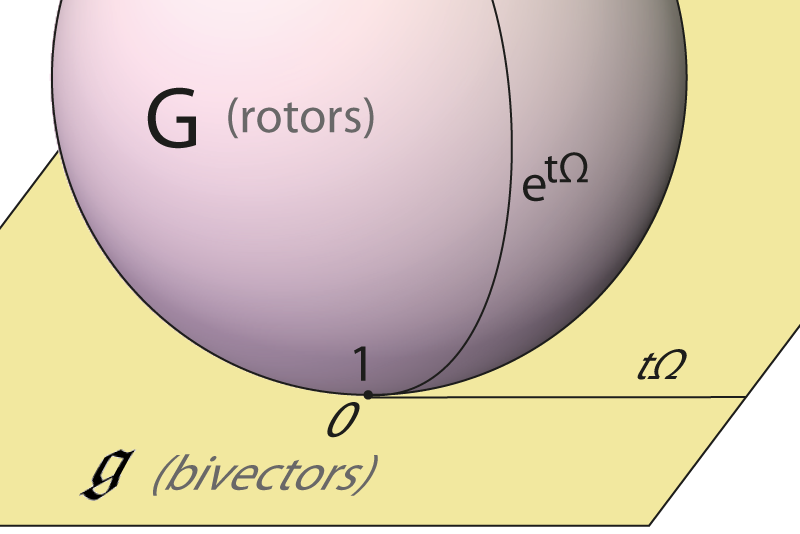
Exponentiating bivectors
The bivectors \(\bigwedge^2\) form the Lie algebra.
Define \(\mathbf{G}\) to be the elements of the even sub-algebra of norm 1. Then \(\mathbf{G}\) is the Lie group.
And \(\exp: \bigwedge^2 \rightarrow \mathbf{G}\) is a 1:1 map up to multiples of \(2\pi\) (for \(n=3\)).
Lie algebra and Lie group
Formula factories via 3-way products
3-way products with a repeated factor of the form \(\mathbf{Y}\mathbf{X}\mathbf{X}\) can be used as formula factories.
Example: \(\mathbf{m} = \mathbf{m}(\mathbf{n}\mathbf{n}) = (\mathbf{m}\mathbf{n})\mathbf{n} \) since for a proper line \(\mathbf{n}^2 = 1\) and associativity. This leads to a decomposition of \(\mathbf{m}\) with respect to \(\mathbf{n}\):

$$(mn)n=(\cos(\alpha)+\sin(\alpha)\mathbf{P})n$$
$$=\cos(\alpha)n + \sin(\alpha)Pn$$
$$=\cos(\alpha)n +\sin(\alpha)P\cdot n$$
$$=\cos(\alpha)n - \sin(\alpha)n\cdot P$$
The arrows show the orientation of the lines.
Formula factories via 3-way products
Examples: Anything can be orthogonally decomposed with respect to anything else! For example ...
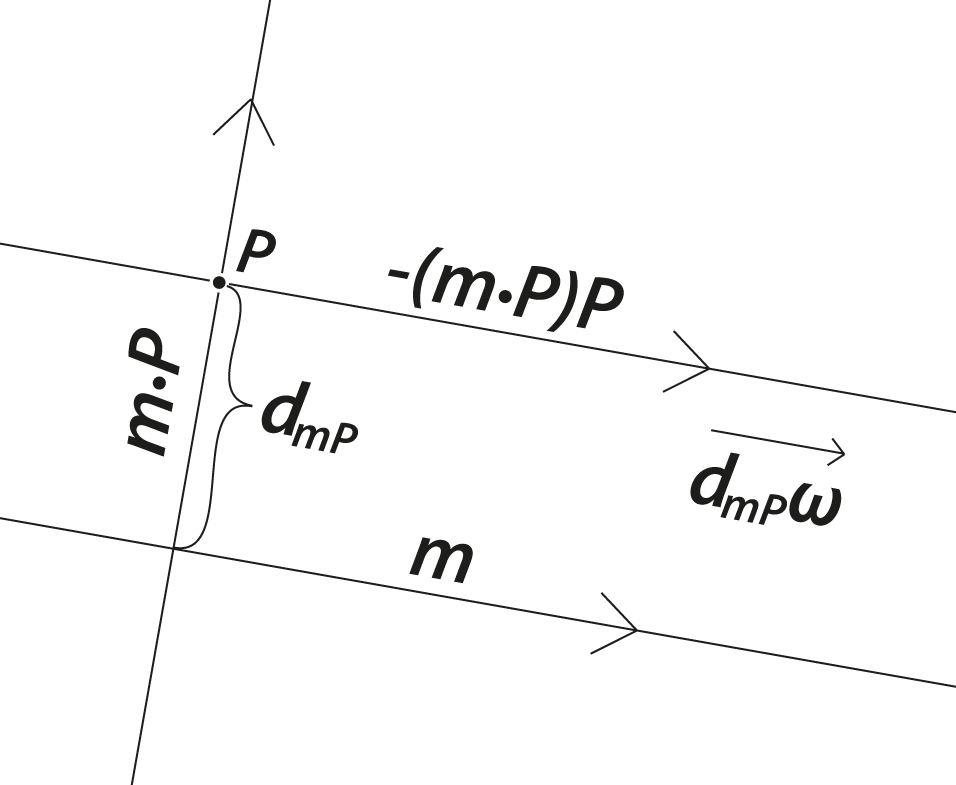
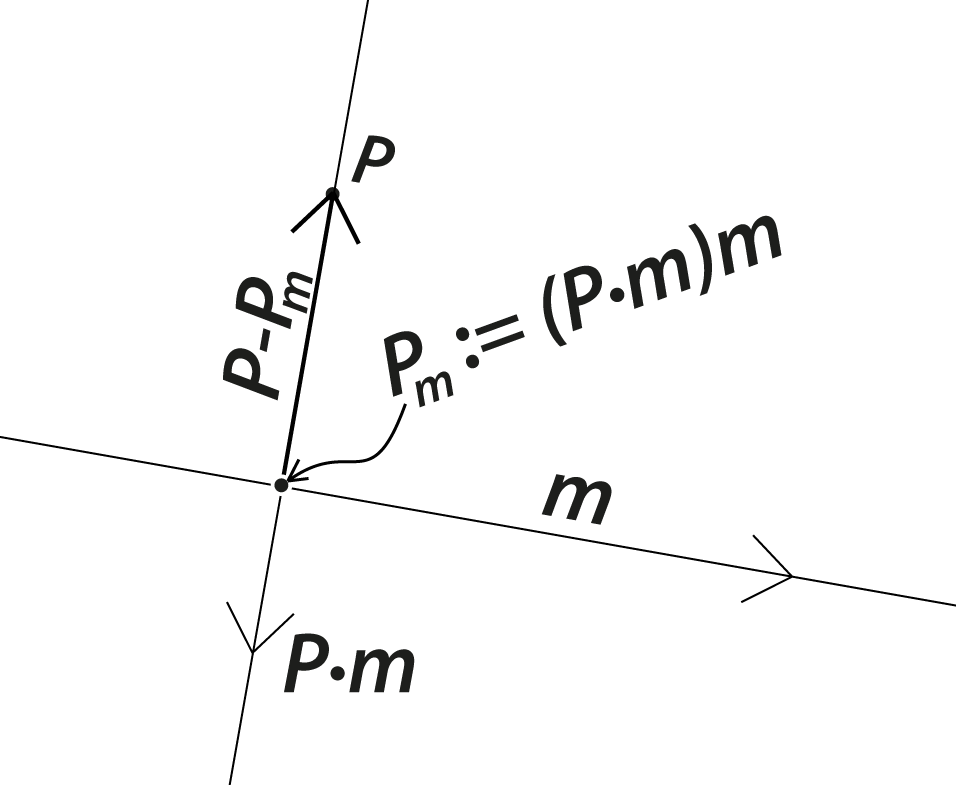
Decompose point WRT line.
Decompose line WRT point.
The pieces of the decomposition are often interesting in their own right. For example, \((P\cdot m)m\) is closest point to \(P\) on \(m\).
Formula factories via 3-way products
General 3-way products \(\mathbf{a}\mathbf{b}\mathbf{c}\) of 1-vectors provide a useful framework for a general theory of triangles. Lots left to do!
2D PGA in the browser
A euclidean demo from Steven De Keninck, using his ganja.js Javascript implementation, showing several of the features discussed above.
\(\ell\) = line (vector)
\(P\) = point (bivector)
\(\ell P\) = line through \(P, \perp\) to \(\ell\)
\(\ell P\ell\) = reflection of \(P\) in \(\ell\)
\(P\ell P\) = reflection of \(\ell\) in \(P\)
\((\ell \cdot P)\ell\) = projection of \(P\) on \(\ell\)
\((P \cdot \ell)P\) = projection of \(\ell\) on \(P\)
Live slides are available at https://slides.com/charlieboy/icerm2019/
Bivectors!

Julius Pluecker
Glimpse at 3D
Glimpse at 3D
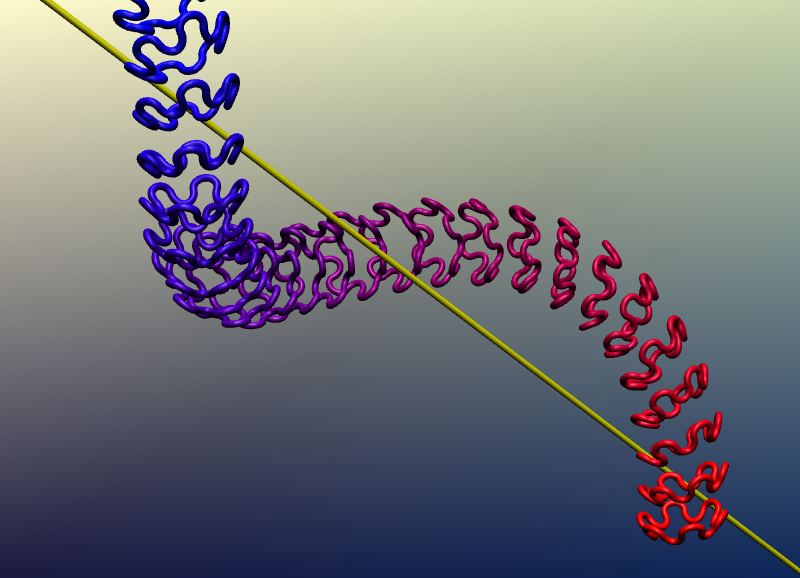
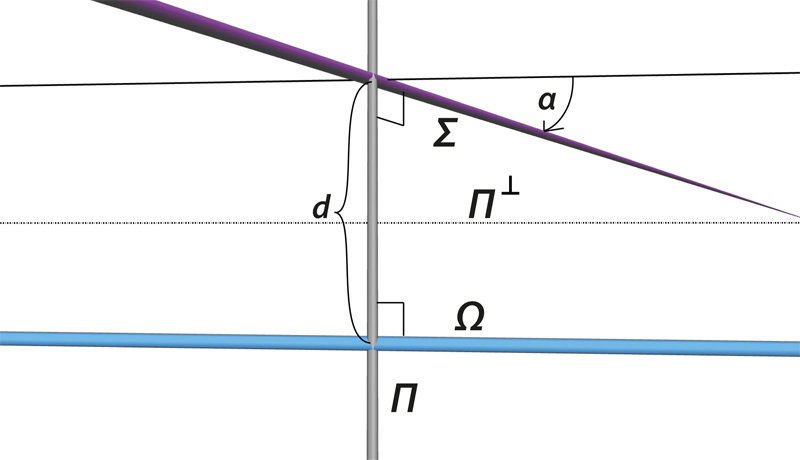

Kinematics and Mechanics
A velocity state is \( \mathbf{V} \in \bigwedge^2\) (in this case a point)
A momentum state is \(\mathbf{M} \in \bigwedge^{n-2}\) (in this case a line)
A rigid body is a collection of Newtonian mass points.
Calculate inertia tensor \(A\) for the body, a quadratic form determined by the mass distribution.
\(\mathbf{M}=A\mathbf{V}\)
ODE's for free top:
PGA equations for the free top in \(P(\mathbb{R}^*_{\kappa})\):
$$\dot{\mathbf{g}} = \mathbf{g} \mathbf{V}~~~~~~~~$$ $$~~~~~~~~~~~ \dot{\mathbf{M}} = \frac12(\mathbf{V}\mathbf{M} - \mathbf{M} \mathbf{V}) $$
where \(\mathbf{g} \in \mathbf{G}\), and \(\mathbf{M}\) and \( \mathbf{V} \)are in the body frame.
2D Kinematics and Mechanics
Advantages of PGA:
- Euclidean case: No splitting into linear and angular parts. A linear velocity is a velocity carried by an ideal point (euclidean). An angular momentum (or force couple) is one carried by the ideal line.
- Similar results hold in 3D.
- The equations are numerically optimal compared to matrix methods. Normalizing \(\mathbf{g}\) keeps it on the solution space.
2D Kinematics and Mechanics
3D Kinematics and Mechanics
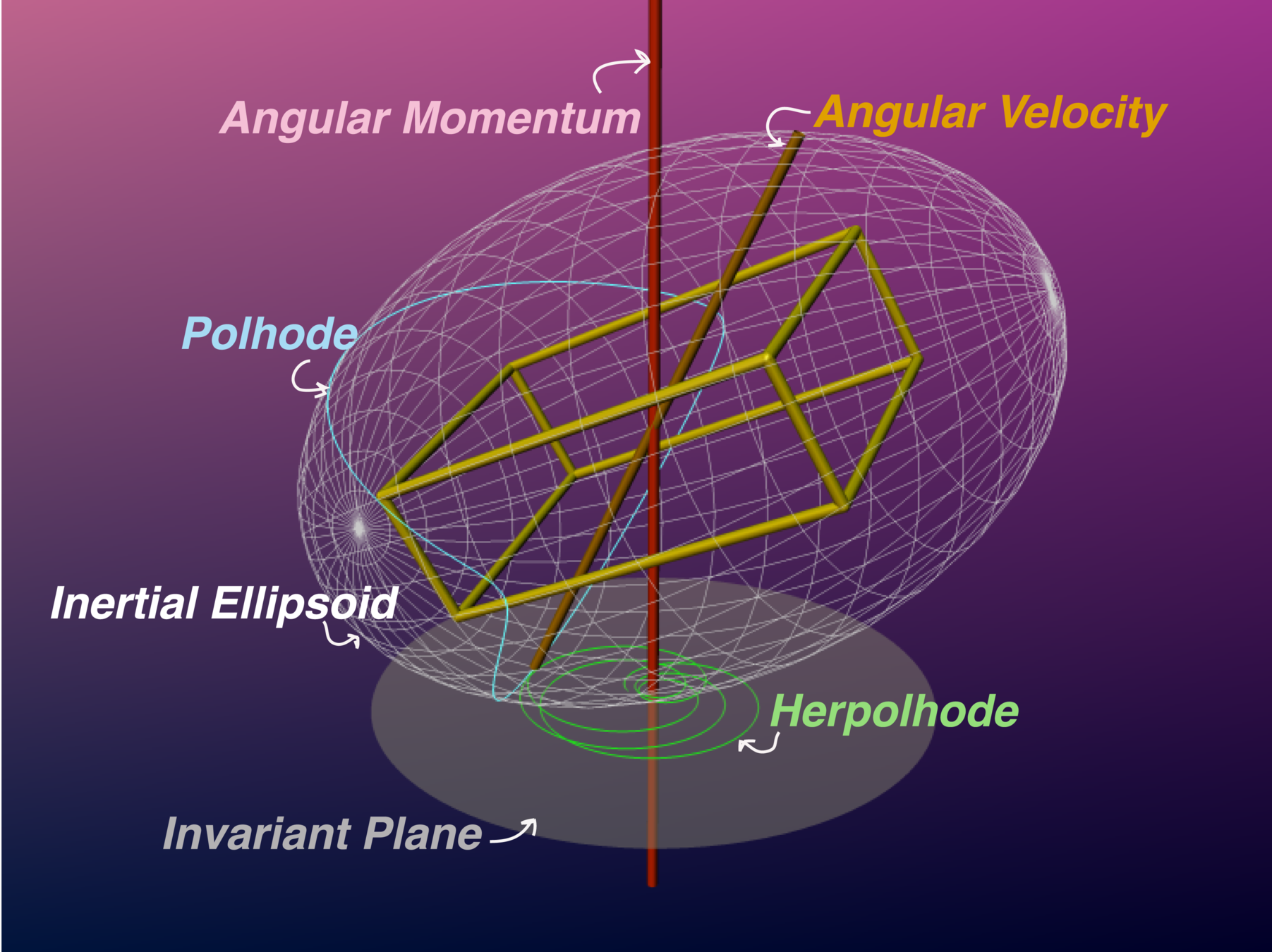

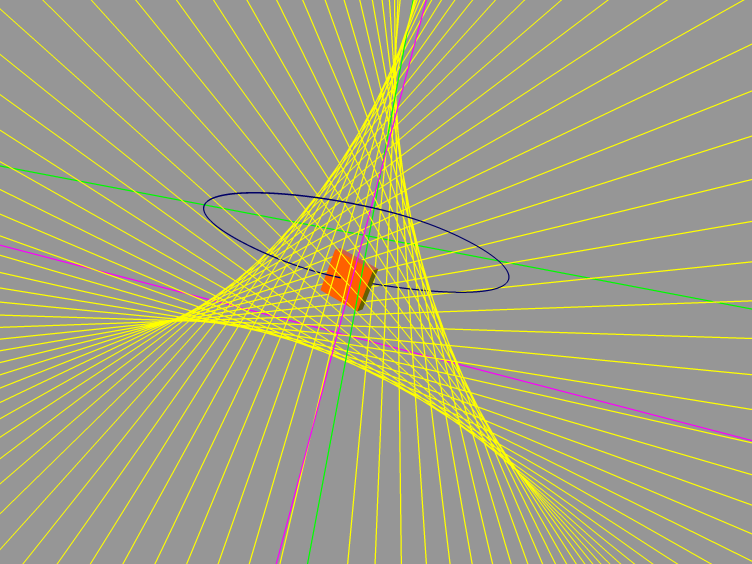


3D
Poinsot motion (?)
Coordinate-free
Uniform rep'n for points, lines, and planes
Cayley-Klein programmer's wish list

Single, uniform rep'n for isometries
Parallel-safe meet and join operators
Compact expressions for classical geometric results
Physics-ready
Metric-neutral
Backwards compatible
Conclusions
- Dual PGA fulfills the "programmers wish list" from the beginning.
- It completes Clifford's project (cut short by his death) of combining Grassmann algebra with all biquaternions, not just the elliptic ones.
- There's a lot left to explore, both in non-euclidean and euclidean, 2D and 3D.
- Team members sought to create browser-based metric-neutral PGA scene graph with physics engine.
- Ask me about ideal norms and dual euclidean space.
Resources


Resources
Metric-neutral resources
Euclidean resources
- bivector.net/doc SIGGRAPH 2019 course notes & cheat sheets & course videos + more.
- Live 2D and 3D PGA demos in JavaScript
- My ResearchGate PGA project
Questions and comments: projgeom at gmail.com
Thanks for your attention!
That's all folks
Partial solutions: Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
III. ODE's for Euler top:
Quaternion equations for the Euler top in \(\mathbb{R}^3\):
$$\dot{\mathbf{g}} = \mathbf{g} \mathbf{V}$$ $$ \dot{\mathbf{M}} = \frac12(\mathbf{V}\mathbf{M} - \mathbf{M} \mathbf{V}) $$
where \(\mathbf{g} \in \mathbb{U}\) and \(\mathbf{M}, \mathbf{V} \in \mathbb{IH}\) are the momentum, resp., velocity vectors in the body frame.
(\(\mathbf{M}={A}\mathbf{V}\) for inertia tensor \(A\)).
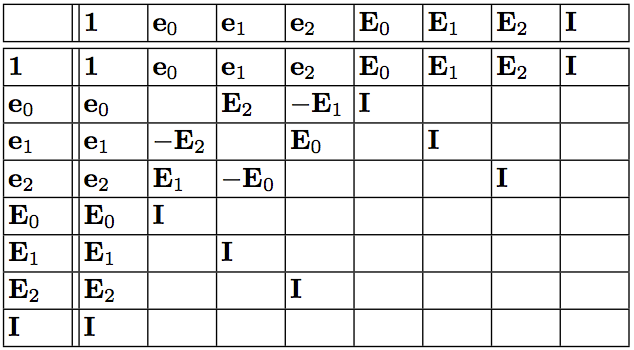
Dual projective Grassmann algebra
Multiplication table for \(\bigwedge\mathbb{R}P^{2\large{*}}\)
Geometric algebra notation
- General multivector is sum of k-vectors: \(\mathbf{a} = \mathbf{\Sigma}_k\langle \mathbf{a}\rangle_k\)
- Points are large letters (\(\mathbf{P}\)) and lines are small (\(\mathbf{m}\)).
- The unit pseudoscalar is written \(\mathbf{I}\).
- The product of a k-vector and an m-vector is a sum $$\mathbf{K}\mathbf{M} = \mathbf{\Sigma}_{i=|k-m|}^{k+m}\langle \mathbf{K}\mathbf{M}\rangle_i$$ where i increases by steps of 2.
- \(\mathbf{K}\wedge\mathbf{M} = \langle \mathbf{K}\mathbf{M}\rangle_{k+m} \)
- \(\mathbf{K}\cdot\mathbf{M} := \langle\mathbf{K}\mathbf{M}\rangle_{|k-m|}\)
- \(\mathbf{K}\times\mathbf{M} := \mathbf{K}\mathbf{M}-\mathbf{M}\mathbf{K}\)
- \(\mathbf{K}\vee\mathbf{M}\) is the join.
The euclidean algebra \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \)
Question: Why is the signature \((2,0,1)\) using the dual construction the proper model for the euclidean plane?

Answer: Given two lines \(\mathbf{m}_i = c_i\mathbf{e}_0+a_i\mathbf{e}_1+b_i\mathbf{e}_2\) (with equations \(a_ix+b_iy+c_i=0\)). Then $$\mathbf{m}_1\cdot\mathbf{m}_2=c_0c_1\mathbf{e}_0^2+a_1a_2\mathbf{e}_1^2+b_1b_2\mathbf{e}_2^2$$ Since the cosine of the angle between the lines is \(a_1a_2 + b_1b_2\), \(\mathbf{e}_0^2=0\) while \(\mathbf{e}_1^2=\mathbf{e}_2^2=1\).
The euclidean algebra \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \)
Question: Why is the signature \((2,0,1)\) using the dual construction the proper model for the euclidean plane?
Answer: Given two lines \(\mathbf{m}_i = c_i\mathbf{e}_0+a_i\mathbf{e}_1+b_i\mathbf{e}_2\) (with equations \(a_ix+b_iy+c_i=0\)). Then $$\mathbf{m}_1\cdot\mathbf{m}_2=c_0c_1\mathbf{e}_0^2+a_1a_2\mathbf{e}_1^2+b_1b_2\mathbf{e}_2^2$$ Since the cosine of the angle between the lines is \(a_1a_2 + b_1b_2\), \(\mathbf{e}_0^2=0\) while \(\mathbf{e}_1^2=\mathbf{e}_2^2=1\).
History: That \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \) models euclidean geometry was first published by Jon Selig in 2000.